Как найти площадь вероятности

Как найти площадь вероятности

Лучшее спасибо – порекомендовать эту страницу

Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие A – это подмножество этой области, пространства элементарных исходов G.

Если для простоты считать, что все точки G «равноправны» (выбор точек равномерен внутри области), то вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.

Геометрическая вероятность события А определяется отношением:
$$
P(A)=frac{m(A)}{m(G)},
$$
где $m(G)$, $m(A)$ – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов $G$ и события $А$ соответственно.

Чаще всего, в одномерном случае речь будет идти о длинах отрезков, в двумерном – о площадях фигур, в трехмерном – об объемах тел.

При этом, некоторые задачи сразу имеют геометрическую интерпретацию (первый пример), а другие выглядят как задачи “про жизнь”, самая распространенная из них – задача о встрече (второй пример).

Основная сложность при решении задач такого типа – построить математическую модель эксперимента, нужным образом выбрать пространство элементарных исходов, обозначить событие, выразить его математически как некоторую область. К сожалению, единого рецепта решения подобых заданий нет, нужно “набить” руку на разных задачах (см. примеры тут, например).

Примеры решений на геометрическую вероятность

Пример. На плоскость, разграфленную параллельными полосами шириной $2d$, расстояние между осевыми линиями которых равно $2D$, наудачу брошен круг радиуса $r$ ($r+dlt D$). Найти вероятность того, что круг пересечет некоторую полосу.

Решение. В качестве элементарного исхода этого испытания будем считать расстояние $x$ от центра круга до осевой линии ближайшей к кругу полосы (ее обозначим за 0). Тогда все пространство элементарных исходов – это отрезок, равный половине расстояния между осями полос $G={x: 0le x le D}$. Его мера – это длина отрезка, то есть $m(G)=D$.

Рассмотрим теперь случаи, благоприятствующие событию $A$ = (Круг пересечет полосу), и найдем меру соответствующей области точек. На чертеже выше покажем различные варианты выпадения круга.

Пересечение круга с полосой очевидно произойдет в том случае, если его центр попадет в полосу (точнее, ее половину), т.е. координата центра круга удовлетворяет неравенству $0 le x le d$, длина этого отрезка $d$.

Также круг пересечет полосу, если его центр будет находится от края полосы на расстоянии меньшем чем радиус (если равен радиусу – круг коснется полосы, если больше – то отстоит от полосы), т.е. когда $d le x le d+r$ (длина этого отрезка $r$).

Тогда вероятность события $A$ по геометрическому определению вероятности:
$$
P(A)=frac{d+r}{D}.
$$

Пример. Два человека договорились встретиться в определенном месте от 17 до 18 часов. При этом каждый обязался после прихода на место встречи ожидать другого 30 минут. Какова вероятность встречи этих людей, если каждый из них равновозможно придет в течение указанного интервала времени?

Решение. Обозначим моменты прихода первого и второго человека за $x$ и $y$. Так как они приходят в промежуток длительности 60 минут (от 17 до 18 часов), то справедливы следующие условия: $0 le x le 60$ и $0 le y le 60$.

Рассмотрим прямоугольную систему координат $xOy$. В этой системе координат всем возможным значениям времени прихода людей соответствуют точки квадрата со стороной 60.

Лица встретятся, если один человек придет раньше, чем уйдет другой, то есть если $y lt x+30$, когда $y gt x$ (второй пришел позже первого, но не позже чем через 30 минут от него) и $x lt y+30$, когда $y lt x$ (первый пришел позже второго, не но позже чем через 30 минут).

Более компактно запишем условия
$$
x lt y lt x+30 quad text{ или } quad x-30 lt y lt x. quad (*)
$$

Построим прямые $y=x$, $y=x-30$, $y=x+30$ и закрасим область, лежащую внутри квадрата, точки которой удовлетворяют условиям (*). Точки этой фигуры (серый шестиугольник в центре) являются благоприятствующими событию $A$ =(люди встретятся).

Тогда искомая вероятность встречи по геометрическому определению вероятности равна отношению площади этой фигуры к площади квадрата:
$$
P=frac{60^2-1/2cdot 30^2-1/2cdot 30^2}{60^2}=frac{3600-900}{3600}=frac{3}{4}=0,75.
$$

Больше примеров на геометрическую вероятность

Источник

Геометрические вероятности:

Область применения классического определения вероятности – испытания с конечным числом равновозможных исходов. Существенным является условие равновозможности. От конечности числа исходов опыта можно отказаться и определять вероятности не с помощью числа исходов, 27 а с помощью отношения длин, площадей и т.д., но при сохранении условия равновозможности.

Геометрическое определение вероятности

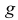
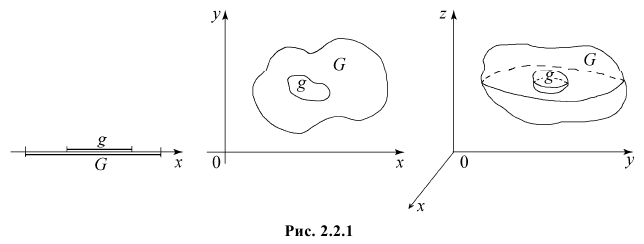
Пусть область Геометрические вероятности - определение и вычисление с примерами решения

Геометрические вероятности - определение и вычисление с примерами решения

Если равновозможно попадание точки в любую точку области G, то вероятность попасть в область 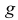Геометрические вероятности - определение и вычисление с примерами решения равна отношению меры области 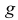Геометрические вероятности - определение и вычисление с примерами решения к мере области G:

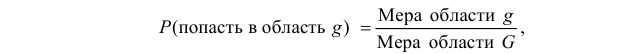
Геометрические вероятности - определение и вычисление с примерами решения

где «мера» – означает: 1) длину, если область G часть прямой или кривой линии; 2) площадь, если G часть плоскости; 3) объем, если G часть пространства, и т.д. в зависимости от характера области G.

Пример:

Две радиостанции течение часа независимо друг от друга должны передать сообщения длительностью 10 мин. и 20 мин. соответственно. Какова вероятность того, что сообщения не перекроются по времени.

Решение. Пусть 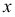Геометрические вероятности - определение и вычисление с примерами решения – момент начала сообщения первой радиостанции, а 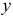Геометрические вероятности - определение и вычисление с примерами решения – момент начала второго сообщения. 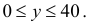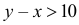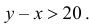Для того чтобы сообщения уложились в отведенный час, должны выполняться условия: Геометрические вероятности - определение и вычисление с примерами решения Сообщения не перекроются во времени, если выполнятся условия: Геометрические вероятности - определение и вычисление с примерами решения и у Геометрические вероятности - определение и вычисление с примерами решения Этим условиям удовлетворяют точки заштрихованных областей, изображенных на рис. 2.2.2.

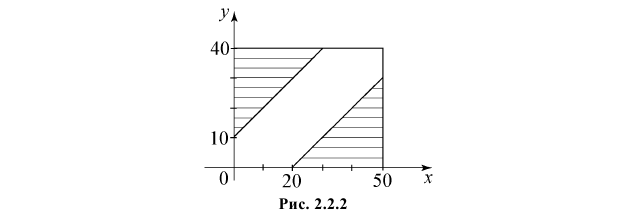
Геометрические вероятности - определение и вычисление с примерами решения

Так как все положения точки 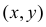Геометрические вероятности - определение и вычисление с примерами решения в прямоугольнике 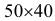Геометрические вероятности - определение и вычисление с примерами решения равновозможны, то искомая вероятность равна отношению заштрихованной площади, которая равна 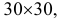Геометрические вероятности - определение и вычисление с примерами решения к площади прямоугольника. Поэтому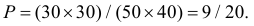 Геометрические вероятности - определение и вычисление с примерами решения

Ответ. 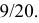Геометрические вероятности - определение и вычисление с примерами решения

Пример:

В треугольник с вершинами A(0;0), B(4;0) и C(0;2) наугад брошена точка, причем все положения точки в этом треугольнике равновозможны. Найдите вероятность того, что координаты точки X и Y будут удовлетворять неравенству 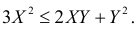Геометрические вероятности - определение и вычисление с примерами решения

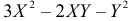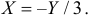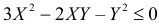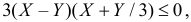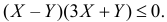Решение. Полагая в квадратном трехчлене Геометрические вероятности - определение и вычисление с примерами решения переменной величиной X, а Y коэффициентом, найдем корни трехчлена X=Y и Геометрические вероятности - определение и вычисление с примерами решения Тогда неравенство Геометрические вероятности - определение и вычисление с примерами решения можно записать в виде Геометрические вероятности - определение и вычисление с примерами решения или Геометрические вероятности - определение и вычисление с примерами решения Последнее неравенство равносильно совокупности неравенств:

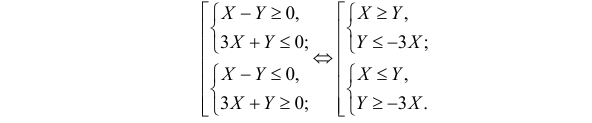
Геометрические вероятности - определение и вычисление с примерами решения

Точки плоскости, координаты которых удовлетворяют этой совокупности систем неравенств, на рис. 2.2.3 выделены штриховкой. Часть из них содержится в треугольнике ABC.

Так как по условию все положения точки 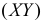Геометрические вероятности - определение и вычисление с примерами решения в треугольнике ABC равновозможны, то по геометрическому определению вероятности искомая вероятность равна отношению площади заштрихованного треугольника AEC к площади треугольника ABC.

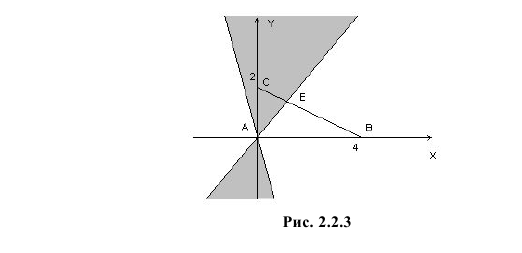
Геометрические вероятности - определение и вычисление с примерами решения

Площадь треугольника ABC равна половине произведения AB на AC, т.е. равна 4. Линия BC имеет уравнение 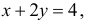Геометрические вероятности - определение и вычисление с примерами решения а линия AE определяется уравнением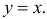 Геометрические вероятности - определение и вычисление с примерами решения

Их точка пересечения имеет координаты E(4/3;4/3). Абсцисса точки E равна высоте треугольника AEC, опущенной на сторону AC. Поэтому площадь треугольника AEC равна 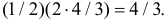Геометрические вероятности - определение и вычисление с примерами решения Поэтому искомая вероятность равна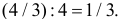 Геометрические вероятности - определение и вычисление с примерами решения

Ответ. 1/3.

Пример:

Координаты случайной точки 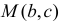Геометрические вероятности - определение и вычисление с примерами решения в треугольнике, ограниченном осями координат и прямой 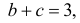Геометрические вероятности - определение и вычисление с примерами решения служат коэффициентами квадратного уравнения 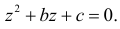Геометрические вероятности - определение и вычисление с примерами решения Полагая все положения случайной точки в указанном треугольнике равновозможными, найти вероятность того, что уравнение имеет два действительных корня.

Решение. Пусть А – интересующее нас событие. Уравнение имеет действительные корни, если его дискриминант 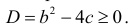Геометрические вероятности - определение и вычисление с примерами решения Это неравенство будет выполнено, если случайная точка М попадет в треугольнике ниже кривой 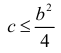Геометрические вероятности - определение и вычисление с примерами решения (на рис. 2.2.4 заштрихованная область). Точка пересечения линий 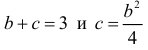Геометрические вероятности - определение и вычисление с примерами решения имеет координаты (2;1). Поэтому площадь заштрихованной фигуры на рис. 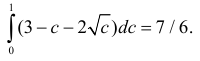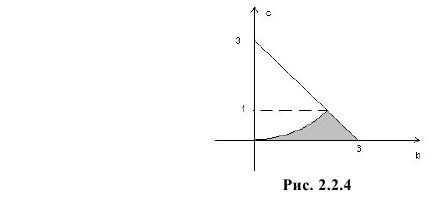2.2.4 равна Геометрические вероятности - определение и вычисление с примерами решения

Геометрические вероятности - определение и вычисление с примерами решения

Так как площадь всего треугольника равна 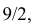Геометрические вероятности - определение и вычисление с примерами решения то по геометрическому определению вероятности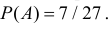 Геометрические вероятности - определение и вычисление с примерами решения

Ответ. 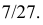Геометрические вероятности - определение и вычисление с примерами решения

Пример:

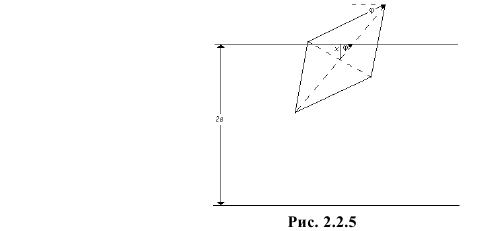
Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстояние 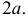Геометрические вероятности - определение и вычисление с примерами решения Острый угол ромба равен 60°, а наибольшая диагональ равна 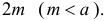Геометрические вероятности - определение и вычисление с примерами решения Ромб наугад бросают на плоскость. Какова вероятность того, что ромб пересечет одну из прямых?

Решение. Бросание ромба «наугад» подразумевает, что центр ромба с равными шансами может оказаться на любом расстоянии 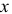Геометрические вероятности - определение и вычисление с примерами решения (в пределах от 0 до 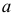Геометрические вероятности - определение и вычисление с примерами решения) от ближайшей прямой, а значения угла 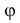Геометрические вероятности - определение и вычисление с примерами решения между наибольшей диагональю и ближайшей прямой равновозможны в пределах от 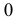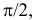Геометрические вероятности - определение и вычисление с примерами решения до 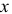Геометрические вероятности - определение и вычисление с примерами решения при этом 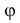Геометрические вероятности - определение и вычисление с примерами решения и Геометрические вероятности - определение и вычисление с примерами решения независимы. Заметим, что расстояние от центра ромба до его стороны равно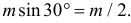 Геометрические вероятности - определение и вычисление с примерами решения

Если 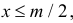Геометрические вероятности - определение и вычисление с примерами решения то ромб несомненно пересечет ближайшую прямую. Если же 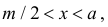Геометрические вероятности - определение и вычисление с примерами решения то для пересечения ближайшей прямой необходимо и достаточно, чтобы 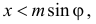Геометрические вероятности - определение и вычисление с примерами решения т.е. проекция половины наибольшей диагонали на перпендикуляр к прямой должна быть больше расстояния от центра ромба до прямой (см. рис. 2.2.5).

Геометрические вероятности - определение и вычисление с примерами решения

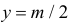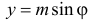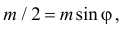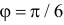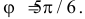Названные условия выполняются в заштрихованной области на рис. 2.2.6. Графики функций Геометрические вероятности - определение и вычисление с примерами решения и Геометрические вероятности - определение и вычисление с примерами решения пересекаются в точках, в которых Геометрические вероятности - определение и вычисление с примерами решения т.е. при Геометрические вероятности - определение и вычисление с примерами решения и Геометрические вероятности - определение и вычисление с примерами решения Поэтому заштрихованная площадь равна

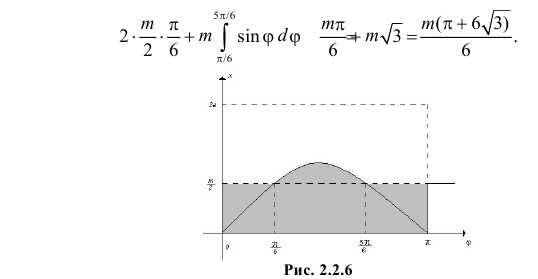
Геометрические вероятности - определение и вычисление с примерами решения

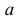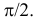Любое положение ромба относительно ближайшей прямой можно охарактеризовать точкой в прямоугольнике со сторонами Геометрические вероятности - определение и вычисление с примерами решения и Геометрические вероятности - определение и вычисление с примерами решения Поскольку все положения ромба относительно ближайшей прямой равновозможны, то по геометрическому определению вероятности искомая вероятность равна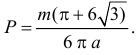 Геометрические вероятности - определение и вычисление с примерами решения

Ответ. 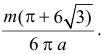Геометрические вероятности - определение и вычисление с примерами решения

Пример:

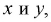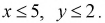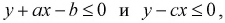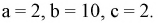
Наудачу взяты два положительных числах Геометрические вероятности - определение и вычисление с примерами решения причем Геометрические вероятности - определение и вычисление с примерами решения Найти вероятность того, что Геометрические вероятности - определение и вычисление с примерами решения если Геометрические вероятности - определение и вычисление с примерами решения

Подставляя значения коэффициентов в неравенства, получаем

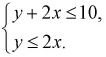
Геометрические вероятности - определение и вычисление с примерами решения

Строим на рис. 1.8 оси координат и область, которая определяет пространство элементарных событий 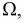Геометрические вероятности - определение и вычисление с примерами решения она задается неравенствами 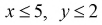Геометрические вероятности - определение и вычисление с примерами решения и отображается на рисунке 1.8 прямоугольником.

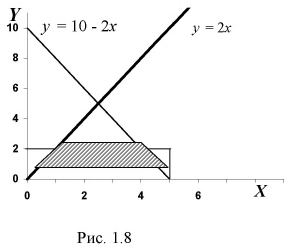
Геометрические вероятности - определение и вычисление с примерами решения

Площадь прямоугольника 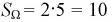Геометрические вероятности - определение и вычисление с примерами решения [условных единиц]. Область благоприятствующих исходов определяется неравенствами 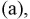Геометрические вероятности - определение и вычисление с примерами решения поэтому строим на рисунке прямые, которые задаются из неравенств 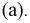Геометрические вероятности - определение и вычисление с примерами решения Заштрихованная на рисунке 1.8 область описывает благоприятствующие исходы (с учетом всех возможных значений) и является трапецией, площадь которой 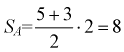Геометрические вероятности - определение и вычисление с примерами решения[условных единиц]. 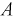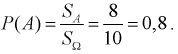Тогда вероятность события Геометрические вероятности - определение и вычисление с примерами решения

Геометрические вероятности - определение и вычисление с примерами решения

Пример:

Найти вероятность того, что на экране радиолокатора отметка от цели появится в кружке радиусом 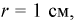Геометрические вероятности - определение и вычисление с примерами решения на азимуте 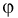Геометрические вероятности - определение и вычисление с примерами решения ноль градусов, на расстоянии 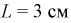Геометрические вероятности - определение и вычисление с примерами решения от центра экрана, если радиус экрана равен 30 см.

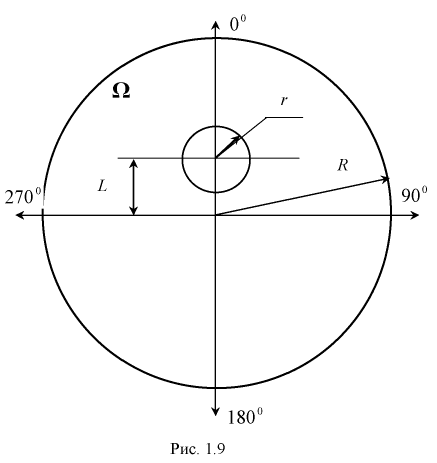
Геометрические вероятности - определение и вычисление с примерами решения

Экран радиолокатора, рис. 1.9, представляет собой электронно-лучевую трубку с радиальной разверткой, в которой от центра до края экрана движется электронный луч и после достижения края движение луча опять начинается от центра к краю, но с некоторым смещением по азимуту. Это перемещение луча от центра экрана соответствует началу излучения радиоимпульса антенного радиолокатора, который укреплен на боковой стенке кабины с передающим устройством, а кабина, в свою очередь, вращается вокруг вертикальной оси, что соответствует смещению луча на экране по азимуту. И когда радиоимпульс отражается от цели, на экране радиолокатора вспыхивает яркая точка. По положению этой точки на экране легко определить расстояние до цели и ее азимут. 

Зная геометрическое определение вероятности, можно сразу сказать, что вероятность появления отметки от цели в кружке радиусом 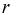Геометрические вероятности - определение и вычисление с примерами решения зависит только от отношения площадей и не зависит ни от формы области благоприятствующих исходов, ни от места ее расположения. Поэтому в этой задаче есть избыточная информация – расстояние 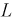Геометрические вероятности - определение и вычисление с примерами решения и азимут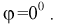 Геометрические вероятности - определение и вычисление с примерами решения

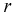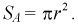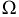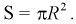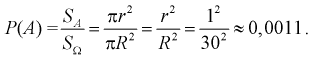
Определяем область благоприятствующих исходов, которой является кружок радиусом Геометрические вероятности - определение и вычисление с примерами решения и площадью – Геометрические вероятности - определение и вычисление с примерами решения Пространство элементарных событий Геометрические вероятности - определение и вычисление с примерами решения – это область экрана, его площадь Геометрические вероятности - определение и вычисление с примерами решения Тогда

Геометрические вероятности - определение и вычисление с примерами решения

  • Теоремы сложения и умножения вероятностей
  • Формула полной вероятности 
  • Повторные независимые испытания
  • Простейший (пуассоновский) поток событий
  • Комбинаторика – правила, формулы и примеры
  • Классическое определение вероятности
  • Элементы теории ошибок
  • Методы математической статистики
Источник

Геометрическая вероятность

  1. Геометрическая вероятность на прямой
  2. Геометрическая вероятность на плоскости
  3. Геометрическая вероятность в пространстве
  4. Примеры

Понятие геометрической вероятности было сформулировано в §37 данного справочника. В этом параграфе мы рассмотрим различные задачи, при решении которых используется геометрическая вероятность.

п.1. Геометрическая вероятность на прямой

В одномерном случае пространству всех событий соответствует длина отрезка Ω ↔ L. Событие A ↔ lA – попадание в отрезок lA ≤ L.
Тогда вероятность события A $$ mathrm{ P(A)=frac{l_A}{L} } $$ Говорят, что мерой множеств событий в одномерном случае является длина.

Например:
Оптический кабель длиной 1 м случайно разрезают ножницами. Какова вероятность того, что длина обрезка составляет не меньше 80 см?
Геометрическая вероятность на прямой
Чтобы получить обрезок не менее 80 см, нужно попасть ножницами в отрезок 20 см справа или слева куска кабеля. Вероятности попадания (mathrm{P_{text{справа}}=frac{l_A}{L}, P_{text{слева}}=frac{l_A}{L}}). По правилу суммы, искомая вероятность при L=100 см, lA=20 см $$ mathrm{ P_{text{справа}}+P_{text{слева}}=frac{2l_A}{L}, P=frac{2cdot 20}{100}=0,4 } $$ Ответ: 0,4.

п.2. Геометрическая вероятность на плоскости

В двумерном случае пространству всех событий соответствует площадь некоторой замкнутой области Ω ↔ SΩ.
Событие A ↔ sA – попадание в замкнутую подобласть с площадью sA ≤ SΩ.
Тогда вероятность события A $$ mathrm{ P(A)=frac{s_A}{S_{Omega}} } $$ Говорят, что мерой множеств событий в двумерном случае является площадь.

Например:
Два друга договорились встретиться между 14 и 15 часами. Каждый может прийти в любой момент в течение назначенного часа. Тот, кто пришёл первым, ждёт другого в течение 15 минут, а затем уходит. Чему равна вероятность встречи?
Геометрическая вероятность на плоскости
Пусть 0≤x≤60 (мин) и 0≤y≤60 (мин) – моменты прихода первого и второго друга соответственно. Тогда пространство событий – квадрат 60х60.
Область ожидания: |x–y|≤15. Раскроем модуль: –15≤x–y≤15. Получаем систему: (left{ begin{array}{ l} mathrm{yleq x+15} &\ mathrm{ygeq x-15} & end{array}right. ). На графике – это зелёная полоса. Событие A – встреча состоялась – соответствует площади зеленой полосы. Получаем: begin{gather*} mathrm{ S_{Omega}=60cdot 60=3600, s_A=3600-2S_{Delta}=3600-2cdot frac{1}{2}cdot 45^2=1575 }\ mathrm{ P(A)=frac{s_A}{S_{Omega}}=frac{1575}{3600}=frac{7}{16}=0,4375 } end{gather*} Ответ: 0,4375.

п.3. Геометрическая вероятность в пространстве

В трёхмерном случае пространству всех событий соответствует объём некоторой замкнутой области Ω ↔ VΩ.
Событие A ↔ vA – попадание в замкнутую подобласть с объёмом vA ≤ VΩ.
Тогда вероятность события A $$ mathrm{ P(A)=frac{v_A}{V_{Omega}} } $$ Говорят, что мерой множеств событий в трёхмерном случае является объём.

Например:
Телескоп находится на космической станции. В каждый момент времени он случайно направлен в одну из сторон и наблюдает часть неба. Пусть телескоп способен регистрировать все объекты в радиусе 10000 км. Какова вероятность, что он заметит астероид радиусом 100 км, залетевший в область регистрации?
Геометрическая вероятность в пространстве
Пространству всех событий соответствует сфера объемом: $$ mathrm{ V_{Omega}=frac{4}{3}pi R^3, R=10000 text{км} } $$ Событие A – астероид замечен – соответствует объему астероида: $$ mathrm{ v_{A}=frac{4}{3}pi R^3, R=100 text{км} } $$ Вероятность того, что астероид будет замечен: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}=frac{frac{4}{3}pi R^3}{frac{4}{3}pi R^3}=left(frac{r}{R}right)^3, P(A)=left(frac{100}{10000}right)^3=10^{-6}=0,000001 } $$ Ответ: 0,000001.

п.4. Примеры

Пример 1. Для игры в «Дартс» используется круглая мишень радиусом 40 см. Центральный круг – «десятка» – имеет радиус 4 см. Если игрок всегда попадает в мишень в любую точку с одинаковой вероятностью, какова вероятность попасть в «десятку»?

Мерой для этой задачи является площадь.
Пространство всех событий – круг радиусом R = 40 см. Его площадь (mathrm{ S_{Omega;}=pi R^2}).
Событие A – попадание в «десятку» – круг радиусом r = 4 см. Его площадь (mathrm{ s_{A}=pi r^2}).
Вероятность попадания: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{pi r^2}{pi R^2}=left(frac{r}{R}right)^2, P(A)=left(frac{4}{40}right)^2=0,01 } $$ Ответ: 0,01.

Пример 2. В правильный треугольник вписан полукруг. В треугольник случайно ставятся точки. Какова вероятность, что точка попадет в полукруг?
Пример 2
Мерой в данной задаче является площадь.
Пусть сторона треугольника a. Тогда пространство всех событий – треугольник площадью (mathrm{ S_{Omega}=frac{sqrt{3}}{4}a^2}).
Найдем радиус вписанного полукруга.
ΔCOB ~ ΔOEB – по двум углам. $$ mathrm{ frac{CO}{OE}=frac{CB}{OB}Rightarrowfrac{acdot sin60^{circ}}{r}=frac{a}{a/2}Rightarrow r=frac{a}{2}cdot sin60^{circ}=frac{sqrt{3}}{4}a } $$ Площадь вписанного полукруга: (mathrm{ s_{A}=frac{pi r^2}{2}=frac{pi}{2}left(frac{sqrt{3}}{4}aright)^2=frac{3pi}{32}a^2}).
Вероятность попасть в полукруг: $$ mathrm{ P(A)=frac{s_{A}}{S_{Omega}}=frac{frac{3pi}{32}a^2}{frac{sqrt{3}}{4}a^2}=frac{sqrt{3}}{8}pi approx 0,68 } $$ Ответ: (mathrm{ frac{sqrt{3}}{8}pi approx 0,68. })

Пример 3. На отрезке [0; 1] случайным образом выбирается точка. Найдите вероятность того, что её координата x удовлетворяет условиям:
1) x2 > 0,64
2) (left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. )

1) (mathrm{x^2geq 0,64Rightarrow (x^2-0,64)geq 0Rightarrow (x-0,8)(x+0,8)geq 0Rightarrow} left{ begin{array}{ l} mathrm{xleq -0,8} &\ mathrm{xgeq 0,8} & end{array}right. )
Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{xleq -0,8Rightarrow 0,8leq xleq 1} &\ mathrm{xgeq 0,8} & end{array}right.& end{array}right. $$ Мерой в данной задаче является длина: LΩ = 1, lA = 1 – 0,8 = 0,2
Вероятность выбора точки при данных условиях: ( mathrm{P(A)=frac{0,2}{1}=0,2} )
begin{gather*} 2) left{ begin{array}{ l} mathrm{0,3x^2leq 0,027} &\ mathrm{2x^2geq 0,08} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2leq 0,009} &\ mathrm{x^2geq 0,004} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{x^2-0,009leq 0} &\ mathrm{x^2-0,004geq 0} & end{array}right. Rightarrow left{ begin{array}{ l} mathrm{(x-0,3)(x+0,3)leq 0} &\ mathrm{(x-0,2)(x+0,2)geq 0} & end{array}right. Rightarrow \ Rightarrow left{ begin{array}{ l} mathrm{-0,3leq xleq 0,3} &\ left[ begin{array}{ l} mathrm{xleq -0,2} &\ mathrm{xgeq 0,2} & end{array}right.& end{array}right. Rightarrow left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right. end{gather*} Учитывая x ∈ [0; 1], получаем: $$ left{ begin{array}{ l} mathrm{0leq xleq 1} &\ left[ begin{array}{ l} mathrm{-0,3leq xleq -0,2} &\ mathrm{0,2leq xleq 0,3} & end{array}right.& end{array}right. Rightarrow 0,2 leq x leq 0,3 $$ Мерой в данной задаче является длина: LΩ = 1, lA = 0,3 – 0,2 = 0,1
Вероятность выбора точки при данных условиях: (mathrm{P(A)=frac{0,1}{1}=0,1})
Ответ: 1) 0,2; 2) 0,1.

Пример 4. В сито, наполненное до краёв зерном, уронили жемчужину. Сито представляет собой цилиндр радиусом 20 см и высотой 12 см.
1) Какова вероятность случайно зачерпнуть горсть зерна вместе с жемчужиной, если объём горсти 0,1 л?
2) Если после неудачной попытки, высыпать зерно из горсти обратно в сито, перемешать, и снова зачерпнуть горсть, изменится ли вероятность?
3) Если после неудачной попытки, высыпать зерно из горсти в сторону и зачерпнуть следующую горсть, изменится ли вероятность?
4) Сколько «неудачных» горстей нужно отсыпать в сторону, чтобы вероятность удачи для следующей попытки превысила 1/3?
1) Мерой для этой задачи является объём.
Пространство всех событий – все возможные точки, где может оказаться жемчужина – это цилиндрическое сито, объемом

VΩ = πR2h,   R = 20 см = 2 дм,  h = 12 см = 1,2 дм
VΩ = π · 22 · 1,2 = 4,8 π дм3 = 4,8 π л

Событие A – зачерпнуть жемчужину в горсти объемом vA = 0,1 л
Вероятность: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}}, P(A)=frac{0,1}{4,8pi} approx 0,0066 } $$ 2) Если высыпать зерно обратно из горсти и перемешать, то пространство всех событий останется тем же, VΩ = 4,8π л. Вероятность не изменится.

3) Если высыпать зерно в сторону, пространство всех событий уменьшится:

V‘Ω = VΩ – vA = (4,8π – 0,1) л

Вероятность увеличится: $$ mathrm{ P(A)=frac{v_{A}}{V_{Omega}^{‘}}, P(A)=frac{0,1}{4,8pi -0,1} approx 0,0071 } $$
4) После того, как мы отсыпаем N горстей, пространство всех событий $$ mathrm{ V_{Omega}^{”} = V_{Omega}-Nv_{A}=(4,8pi-0,1N) text{л} } $$ По условию: $$ mathrm{ P(A)frac{0,1}{4,8pi -0,1N}geq frac13 } $$ Получаем: (mathrm{4,8pi -0,1Nlt 0,3Rightarrow Ngt frac{4,8pi-0,3}{0,1}=147,8})
N = 148.
Ответ: 1) 0,0066; 2) нет; 3) увеличится, 0,0071; 4) 148.

Пример 5. Загадываются два действительных числа от 0 до 4.
1) Какова вероятность, что их сумма больше 3?
2) Какова вероятность, что их разность меньше 1?

По условию 0 ≤ x ≤ 4, 0 ≤ y ≤ 4
Мерой для этой задачи является площадь.
Пространство всех событий: квадрат 4х4, SΩ = 42 = 16.

Ответ: (mathrm{ 1) frac{23}{32}; 2) frac{7}{16}. })

Источник

Классическая
формула вероятности предполагает
конечное число всех исходов испытания.
Но часто встречаются такие испытания,
для которых число возможных исходов
бесконечно. В подобных случаях классическая
формула вероятности не применима и в
этом заключается один из недостатков
классического определения вероятности.
Например, в теории стрельбы точность
попадания равна расстоянию от центра
мишени до точки попадания и может
принимать любое значение. Если под
опытом понимать один выстрел, то в
результате такого опыта возможно
бесконечное множество исходов.

Геометрической
вероятностью
события
А называется отношение меры области g,
благоприятствующей появлению события
А, к мере всей области G,

в каждой точке которой с равной
вероятностью могут осуществляться
исходы рассматриваемого опыта:


(1.7)

Мера
– это сложное математическое понятие.
В простейшем случае это может быть длина
(для одномерных областей, например,
длина какой-нибудь кривой), площадь
(для двухмерных областей, например,
площадь какой-нибудь поверхности), объем
(для трехмерных областей, например,
объем некоторого тела в пространстве).

Пример
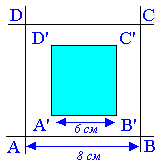
1.15. На
плоскость нанесена сетка квадратов со
стороной 8 см. Найти вероятность того,
что брошенный на плоскость круг радиуса
1 см не пересечет ни одной стороны
квадрата (событие А).

Решение.
При бросании круга его центр может
попасть с равной вероятностью в любой
из квадратов, начерченных на плоскости.
Поскольку все квадраты одина­ковы,
то, не уменьшая общности, можно рассмотреть
только один квадрат. Сделаем внутри
квадрата “рамку” шириной 1 см. Если
центр круга попадет в “рамку”, то
круг обязательно пересечет сторону
квадрата. Если же центр круга попадет
в заштрихованную область, то он не
пересечет ни одной стороны квадрата.
Таким образом, заштрихованный квадрат
является благоприятствующей областью
наступления события А, вероятность
которого нужно найти. В результате
получаем:

Геометрический
поход к вычислению вероятностей можно
использовать в некоторых случаях и для
негеометрических задач:

Пример 1.16.
Два человека А и В решили встретиться
между 9 и 10 часами. Причем каждый ждет
друг друга в течение 20 мин. Чему равна
вероятность того, что они встретятся,
если моменты прихода каждого из них в
течение указанного времени равновероятны.

Решение.
Обозначим моменты прихода лица А через
x,
а лица В
через y.
Для того
чтобы встреча состоялась, необходимо
и достаточно, чтобы

Примем
x
и
y
в качестве
декартовых
координат на плоскости xOy.
Тогда всевозможные исходы будут
изображаться точками квадрата;
благоприятствующие встрече – располагаться
в заштрихованной области (см. рис.).
Искомая вероятность равна отношению
площади заштрихованной фигуры к площади
всего квадрата:

1.9. Статистическое определение вероятности

Классическое
определение вероятности при переходе
от простейших примеров к рассмотрению
сложных задач, в особенности же задач
естественнонаучного или технического
характера, становится не применимым.
Прежде всего здесь возникает вопрос о
возможности нахождения разумного
способа выделения “равновоз­можных”
событий. Как, например, из соображений
симметрии, на которых основаны наши
суждения о равновероятности событий,
вывести вероятность распада радиоактивного
вещества за определенный промежуток
времени; или как определить вероятность
того, что родившийся ребенок окажется
мальчиком. В этих случаях, еще на заре
возникновения теории вероятностей, был
найден иной способ приближенной оценки
неизвестной вероятности случайного
события.

Относительной
частотой
появления события А называется отношение

(1.8)

где
n
– число
опытов, m
– число
появлений события А.

Длительные
наблюдения над появлением и непоявлением
события А при большом числе независимых
испытаний, производимых при одном и том
же комплексе условий, в ряде случаев
показывают, что число появлений события
А подчиняется устойчивым закономерностям.
Еще в XVII
в. Я. Бернулли
доказал (см. закон
больших чисел Бернулли),
что при
неограниченном увеличении числа опытов
относительная частота будет практически
сколь угодно мало отличаться от некоторого
постоянного числа, которое и принимается
за вероятность события в отдельном
опыте.

Статистической
вероятностью
называется относительная частота
появления события при неограниченном
увеличении числа испытаний:

(1.9)

Примером
статистической вероятности может
являться число 0,514 – средне статистическая
вероятность рождения мальчиков.
Статистическое определение вероятности
широко используется на практике, особенно
в естествознании. Здесь для определения
вероятности используются различные
методы математической статистики. Более
того, статистическое определение
вероятности немецкий математик Р. Мизес
положил в основу частотной теории
вероятностей. Однако при таком подходе
теория вероятностей будет всего лишь
прикладной наукой, в которой широко
используются математические методы.
Отметим, что статистический подход к
определению вероятности обладает рядом
недостатков. Во-первых, объективно
невозможно осуществить произвольное
число испытаний; во-вторых, статистическую
вероятность можно определить только
после опыта, по его результатам, т.е.
статистический подход не обладает
предсказательной силой.

В
заключение отметим, что между всеми
рассматриваемыми определениями
вероятности (классическим, геометрическим,
статистическим) нет принципиального
различия. Все они являются всего лишь
различными походами к определению одной
и той же объективной реальности, которая
называется вероятностью.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник


2.4.3. Функция ПЛОТНОСТИ распределения вероятностей

или дифференциальная функция распределения. Она представляет собой производную функции распределения: .

Примечание: для дискретной случайной величины такой функции не существует

В нашем примере:

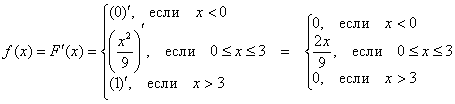
то есть, всё очень просто – берём производную от каждого куска, и порядок.

Но настоящий порядок состоит в том, что несобственный интеграл от с пределами интегрирования от «минус» до «плюс» бесконечности:

 – равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция была найдена как производная, то  – не является функцией распределения (несмотря на какие бы то ни было другие признаки).

Проверим «подлинность» наших функций. Если случайная величина  принимает значения из конечного промежутка, то всё дело сводится к вычислению определённого интеграла. В силу свойства аддитивности, делим интеграл на 3 части:

Совершенно понятно, что левый и правый интегралы равны нулю и нам осталось вычислить средний интеграл:
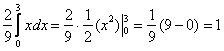, что и требовалось проверить.

С вероятностной точки зрения это означает, что случайная величина  достоверно примет одно из значений отрезка . Геометрически же это значит, что площадь между осью  и графиком  равна единице, и в данном случае речь идёт о площади треугольника .  Сторона  является фрагментом прямой  и для её построения достаточно найти точку :

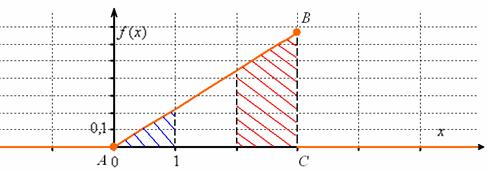
Ну вот, теперь всё наглядно – где бОльшая площадь, там и сконцентрированы более вероятные значения.

Так как функция плотности «собирает под собой» вероятности, то она неотрицательна  и её график не может располагаться ниже оси . В общем случае функция разрывна (смотрим, где «жирные» оранжевые точки!).

Теперь разберём весьма любопытный факт: поскольку действительных чисел несчётно много, то вероятность того, что случайная величина  примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадываетесь:
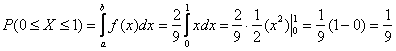 (синяя площадь на чертеже)  – вероятность того, что случайная величина примет значение из отрезка ;
 (красная площадь) – вероятность того, что случайная величина примет значение из отрезка .

По той причине, что отдельно взятые значения можно не принимать во внимание, с помощью этих же интегралов рассчитываются и вероятности по интервалам и полуинтервалам, в частности:

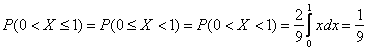
Этим же объяснятся аналогичная «вольность» с функцией .
Возможно, кто-то спросит: а зачем считать интегралы, если есть функция ?

А дело в том, что во многих задачах непрерывная случайная величина ИЗНАЧАЛЬНО задана функцией  плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию  (с помощью тех же интегралов), после чего использовать «лёгкий способ» бросить курить отыскания вероятностей. Впрочем, об этом чуть позже:

Задача 105
Непрерывная случайная величина  задана своей функцией распределения:

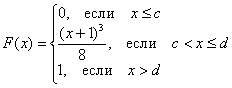
Найти значения  и функцию . Проверить, что  действительно является функцией плотности  распределения. Вычислить вероятности . Построить графики .

Тренируемся самостоятельно! Если возникнут затруднения, то внимательно перечитайте вышеизложенный материал. Краткое решение и ответ в конце книги.

Вообще, типовые задачи на непрерывную случайную величину можно разделить на 2 большие группы:

1) когда дана функция , 2) когда дана функция .

В первом случае не составляет особых трудностей отыскать функцию плотности распределения  – почти всегда производные не то что простЫ, а примитивны (в чём мы только что убедились). Но вот когда НСВ задана функцией , то нахождение функции распределения – есть более кропотливый процесс:
Задача 106
Непрерывная случайная величина  задана функцией плотности распределения:

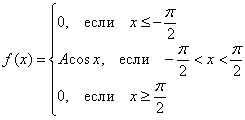
Найти значение  и составить функцию распределения вероятностей . Вычислить .
Построить графики .

Решение: найдём константу . Это классика (в подавляющем большинстве задач вам не предложат готовую функцию плотности). Используем свойство .
В данном случае:

На практике нулевые интегралы можно опускать, а константу сразу выносить за знак интеграла:
            (*)
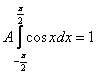Пользуясь чётностью подынтегральной функции, вычислим интеграл:
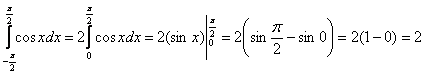 и подставим результат в уравнение (*):
, откуда выразим

Таким образом, функция плотности распределения:

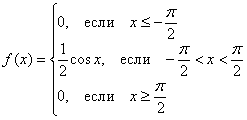
Выполним проверку, а именно, вычислим тот же самый интеграл, но уже с известной константой. Для разнообразия я не буду пользоваться чётностью:
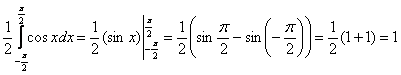, отлично.

Обратите внимание, что только при  и только при этом значении предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале , т.е. условие неотрицательности действительно выполнено. Доверяй условию, да проверяй 😉 Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.

Теперь начинается самое интересное. Функции распределения вероятностей – есть интеграл:

Так как  состоит из трёх кусков, то решение разобьётся на 3 шага:

1) На промежутке , поэтому:

2) На интервале , и мы прицепляем следующий вагончик:

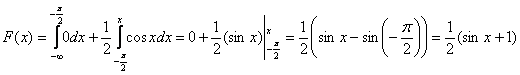
При подстановке верхнего предела интегрирования можно считать, что вместо «икс» мы подставляем «икс». Если же возник вопрос с пределом нижним, то вспоминаем график синуса либо его нечётность: .

3) И, наконец, на , и детский паровозик отправляется в путь:

Внимание! А вот в этом задании нулевые интегралы пропускать НЕ НАДО. Чтобы показать своё понимание функции распределения 😉 К тому же, они могут оказаться вовсе не нулевыми, и тогда придётся иметь дело с интегралами несобственными. И такой пример я обязательно разберу ниже.

Записываем наши достижения под единую скобку:

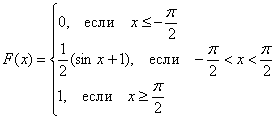
С высокой вероятностью всё правильно, но, тем не менее, устно возьмём производную: 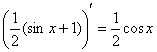, а также «прозвоним» точки «стыка»:

Правильность решения можно проконтролировать и в ходе построения графика, но, во-первых, он не всегда требуется, а во-вторых, до сего момента можно успеть «наломать дров». Ибо вероятности попадания чаще находят с помощью функции распределения:

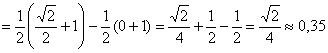 – вероятность того, что случайная величина  примет значение из промежутка

Второй способ состоит в вычислении интеграла:
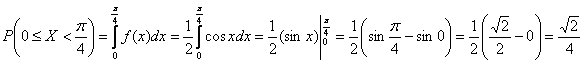что, кстати, не труднее. И проверочка заодно получилась.

Выполним чертежи. График  представляет собой косинусоиду, сжатую вдоль ординат в 2 раза. Тот редкий случай, когда функция плотности непрерывна:

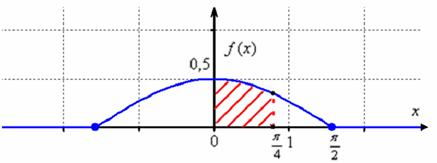
Значение  численно равно заштрихованной площади – это я специально нарисовал, чтобы напомнить вероятностный смысл плотности функции распределения. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала . Заметьте, что значения  по условию, невозможны.
Осталось изобразить функцию распределения. График  представляет собой синусоиду, сжатую в 2 раза вдоль оси ординат и сдвинутую на  вверх:

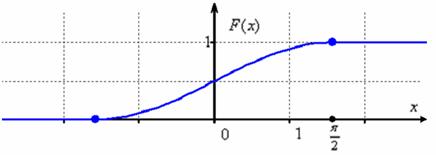
В принципе, тут можно было не заморачиваться преобразованием графиков, а найти несколько опорных точек и догадаться, как выглядит кривая (тригонометрическая таблица в помощь). Но «любительский» подход чреват тем, что график получится принципиально не точным. Так, в нашем примере в точке  существует перегиб графика функции , и велик риск неверно отобразить его выпуклость / вогнутость.

Чертежи желательно расположить так, чтобы оси ординат (вертикальные оси) лежали ровненько одна под другой. Это будет хорошим тоном.

И я так чувствую, вам уже не терпится проверить свои силы. Как водится, пример попроще:

Задача 107
Задана плотность распределения вероятностей непрерывной случайной величины :

Требуется:

1) определить коэффициент ;
2) найти функцию распределения ;
3) построить графики ;
4) найти вероятность того, что  примет значение из промежутка

и задачка поинтереснее:

Задача 108
Непрерывная случайная величина  задана плотностью распределения вероятностей:

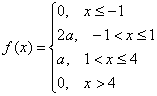
Найти значение  и построить график плотности распределения. Найти функцию распределения вероятностей  и построить её график. Вычислить вероятность .

Дерзайте! Свериться с решением можно внизу книги.

Следует отметить, что все эти задачи реально предлагают студентам-заочникам, и поэтому я не предлагаю вам ничего необычного.

И в заключение параграфа обещанные случаи с несобственными интегралами:

Задача 109
Непрерывная случайная величина  задана своей плотностью распределения:

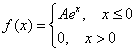
Найти коэффициент  и функцию распределения . Построить графики.

Решение: по свойству функции плотности распределения:

В данной задаче  состоит из 2 частей, поэтому:

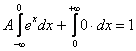
Правый интеграл равен нулю, а вот левый – есть «живой» несобственный интеграл с бесконечным нижним пределом:

Таким образом, наше уравнение превратилось в готовый результат:

и функция плотности:

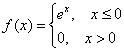
Функция , как нетрудно понять, отыскивается в 2 шага:

1) На промежутке , следовательно:
 – вот такая вот у нас замечательная экспонента. Как птица Феникс.

2) На интервале   и:
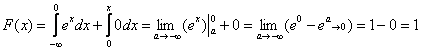, что и должно получиться.

Для построения графиков найдём пару опорных точек:  и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:

Заметьте, что теоретически случайная величина  может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при .

В соответствующей статье сайта я рассмотрел ещё более интересный пример с функцией , где случайная величина теоретически принимает вообще ВСЕ действительные значения. Но это уже несколько повышенный уровень сложности.

2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?

2.4.2. Вероятность попадания в промежуток

| Оглавление |



Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Добавить комментарий