Как найти площадь восьмиугольника вписанного в квадрат

Let us name all the points on the outer square like this:

So, AB, CD, EF, AD are side of the square of length say $mathrm{a}$ and E, F, G and H are midpoints of the sides of the square. Now consider line segments AF, GC, BH, ED. AF and GC intersect BH and ED to form another square.

The area of this square is $frac{a^2}{5}$ as proved from answers to this question. So, side of this square is $frac{a}{sqrt{5}}$. The sides of the square act as span of the octagon (S).(See octagon).

Line HC, AE, GD, FB not drawn for clarity.

Area of octagon in terms of span = $mathrm{2(sqrt{2}-1)S^2 = 2(sqrt{2}-1)frac{a^2}{5} = frac{2(sqrt{2}-1)}{5}{a^2}}$

Therefore, ratio between the area of the octagon and the area of the square = $mathrm{frac{2(sqrt{2}-1)}{5}}$

Восьмиугольник – это геометрическая фигура из мира многоугольников; восьмиугольник имеет 8 сторон и 8
углов или вершин. Правильный многоугольник представляет собой выпуклый многоугольник с равенством
всех сторон и всех углов при вершинах. Следовательно, правильный восьмиугольник – это выпуклый
восьмиугольник, с равенством 8 сторон и 8 углов при вершинах. Другое название фигуры – октагон, от
латинского octo», что означает «восемь». Иногда требуется узнать площадь геометрической фигуры по
некоторым ее известным размерам, например, с целью узнать расход материала на изготовление, заливку,
окраску; или же массу в отсутствие весов при известной толщине многоугольной плитки и плотности
материала.

Для вычисления площади октагона необходимо знать его периметр, который в данном случае равен сумме
длин его 8 сторон (восьмикратной длине одной стороны), и апофему. В планиметрии апофемой называется
длина перпендикуляра, опущенного из центра правильного многоугольника на любую из его сторон.

При известной апофеме площадь правильного многоугольника равна произведению периметра на апофему,
деленному на 2 (в пределе эта формула справедлива даже для круга, где «апофема» равна радиусу).
Поскольку периметр в рассматриваемом случае равен длине стороны, умноженной на 8, искомый параметр
найдется как произведение длины стороны на апофему, умноженный на 4.

Через длину стороны

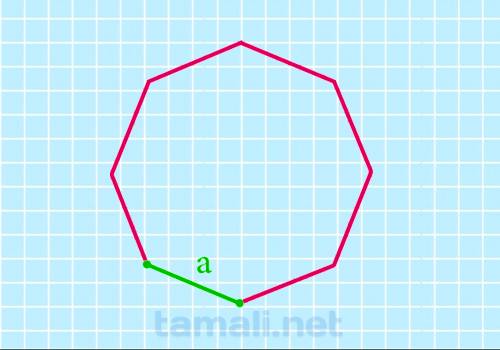
Если апофема неизвестна, ее можно узнать по длине стороны a, исходя из тригонометрических
соотношений, и тогда искомая площадь определится как

S = 2 * a² * (1 + √2)

Пример вычисления: при длине стороны a=8 м площадь равна 4,828 * 8² = 309 кв.м.

Через радиус вписанной окружности

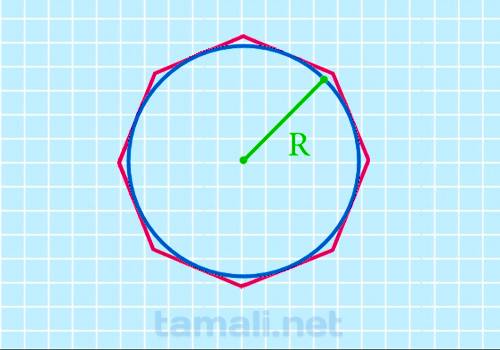
Поскольку апофема является радиусом вписанной окружности r, появляется возможность вычислить площадь
через радиус вписанной окружности:

S = 8 * r² * (√2 — 1)

Пример: при радиусе вписанной окружности 15 м площадь равна 3,314 * 15² = 746 кв.м.

Через радиус описанной окружности

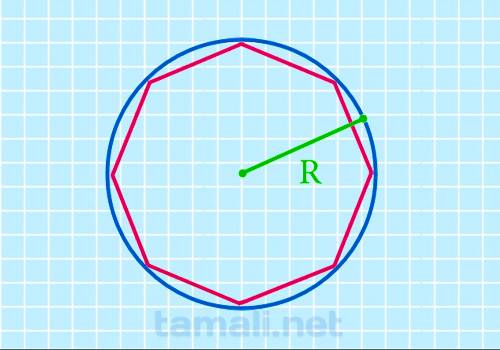
При знании лишь радиуса описанной окружности R возможно вычисление площади по формуле:

S = 2 * √2 * R²

Пример: при радиусе описанной окружности 9 м площадь равна 2,828  92 = 229 кв.м.

Свойства правильного восьмиугольника

Сумма внутренних углов любого выпуклого восьмиугольника равна 1080°, отсюда угол при его вершине
равен 1080°/8=135°. В правильном восьмиугольнике всего 20 диагоналей; длина четырех самых длинных из
них равна двум радиусам описанной окружности.

В природе восьмиугольники встречаются не так часто, как шестиугольники (поскольку восьмиугольники, в
отличие от шестиугольников, не могут заполнить плоскость), но примеры можно найти.

Распространение правильного восьмиугольника в быту и окружающей жизни

Восьмиугольная форма – распространенный архитектурный элемент дизайна. Купол мусульманского святилища
Скала в Иерусалиме в плане октагон. Подобная форма также распространена в архитектуре, например, в
соборе Святого Георгия (Аддис-Абеба), базилике Сан-Витале (Равенна, Италия), Кастель дель Монте
(Апулия, Италия), баптистерии во Флоренции, церкви Цум Фридефюрстен (Германия) и ряде норвежских
церквей. Центральное помещение Ахенского собора, Каролингская Палатинская капелла, также имеет форму
октагона.

Мистики считали, что октагон объединяет «ограниченность земного и бесконечность небесного круга»,
объединяет Бога и человека, жизнь и смерть.

Восьмиугольная планировка пола использовалась в зданиях для разделения офисов и служб здания;
например, в штаб-квартире Intelsat в Вашингтоне, офисах Callam в Канберре и офисах Octagon в
Парраматте, Австралия.

Запрещающий дорожный знак «Движение без остановки запрещено» имеет форму красного правильного
восьмиугольника с надписью STOP в России и ряде многих других стран.

Найдем строну квадрата

   см

Если из центра восьмиугольника провести отрезки соединяющие вершины, то вписанный многоугольник будет разбит на восемь одинаковых равнобедренных треугольников. Боковая торона которых будет равна радиусу описанной окружности или половине диаметра.

см

Учитывая, что отрезки делят окружность на 8 равных частей, то угол при вершине будет равен

Найдем прощать такого треугольника через стороны и угол между ними

Площадь восьмиугольника в 8 раз больше площади треугольника

Ответ: