Онлайн калькулятор площади вписанного в круг квадрата. Как узнать площадь вписанного в круг квадрата.






Вычислить площадь вписанного квадрата через:
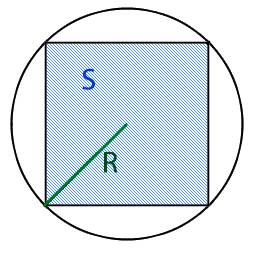
Радиус круга R:
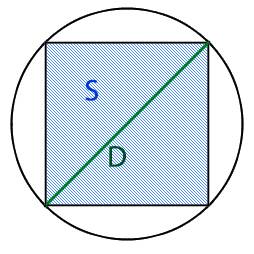
Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.
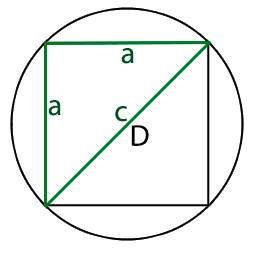
Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
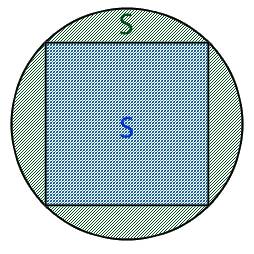
- либо площадь круга, обозначаемая буквой S,
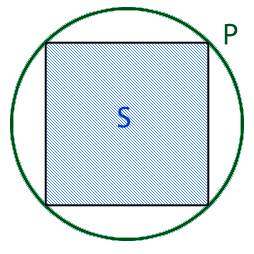
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
мы можем узнать длину сторон квадрата используя теорему Пифагора
после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.
Как определить площадь квадрата

О чем эта статья:
3 класс, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a 2 , где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d 2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r 2 , где r — это радиус вписанной окружности.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R 2 , где R — это радиус описанной окружности.
У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р 2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Воспользуемся формулой: S = d 2 : 2.
Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .
Ответ: 4050 мм 2 .
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d
Диаметр окружности равен двум радиусам:
d = 2r
Получается, что сторона равна двум радиусам:
a = 2r
Используем формулу нахождения площади квадрата через сторону:
S = a 2
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2
Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2
Квадрат вписанный в окружность
Определение
Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.
На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.

Формулы
Радиус вписанной окружности в квадрат
- Радиус вписанной окружности в квадрат, если известна сторона:
Радиус вписанной окружности в квадрат, если известен периметр:
Радиус вписанной окружности в квадрат, если известна площадь:
Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:
Радиус вписанной окружности в квадрат, если известна диагональ:
Радиус описанной окружности около квадрата
- Радиус описанной окружности около квадрата, если известна сторона:
Радиус описанной окружности около квадрата, если известен периметр:
Радиус описанной окружности около квадрата, если известнаплощадь:
Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:
Радиус описанной окружности около квадрата, если известнадиагональ:
Сторона квадрата
- Сторона квадрата вписанного в окружность, если известнаплощадь:
Сторона квадрата вписанного в окружность, если известнадиагональ:
Сторона квадрата вписанного в окружность, если известен периметр:
Площадь квадрата
- Площадь квадрата вписанного в окружность, если известна сторона:
Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:
Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:
Площадь квадрата вписанного в окружность, если известен периметр:
Площадь квадрата вписанного в окружность, если известна диагональ:
Периметр квадрата
- Периметр квадрата вписанного в окружность, если известна сторона:
Периметр квадрата вписанного в окружность, если известна площадь:
Периметр квадрата вписанного в окружность, если известенрадиус вписанной окружности:
Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:
Периметр квадрата вписанного в окружность, если известна диагональ:
Диагональ квадрата
- Диагональ квадрата вписанного в окружность, если известна сторона:
Диагональ квадрата вписанного в окружность, если известна площадь:
Диагональ квадрата вписанного в окружность, если известен периметр:
Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:
Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/ploshad-kvadrata
http://colibrus.ru/kvadrat-vpisannyy-v-okruzhnost/
[/spoiler]
При помощи нашего калькулятора вы легко сможете узнать площадь вписанного в круг квадрата.
Для того что бы найти площадь вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:
- либо площадь круга, обозначаемая буквой S,
- либо периметр круга, обозначаемый буквой P,
- либо радиус круга, обозначаемый буквой R,
- либо диаметр круга, обозначаемый буквой D.
Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой
c2 = 2a2,
Таким образом
a =
√
c2/2
Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга
D = c
1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=P/π
3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:
D=2R
Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,
c=D
мы можем узнать длину сторон квадрата используя теорему Пифагора
после того как мы получили значение длины стороны вписанного квадрата равную a, для получения его площади нам необходимо полученное значение возвести в квадрат.
S = a2
По какой формуле найти площадь квадрата, вписанного в окружность?
Венера Цвирова
Знаток
(442),
закрыт
9 лет назад
Дополнен 13 лет назад
Зная только диаметр окружности
Лучший ответ
Биржан Акинкожаев
Ученик
(176)
13 лет назад
s=2(R*2)(в квадрате, R-радиус)
Остальные ответы
klofelin1988@mail.ru
Профи
(655)
13 лет назад
S=(p−a)(p−b)(p−c)(p−d), где p=a+b+c+d деленное на 2 может так???
Paul Top
Мыслитель
(8988)
13 лет назад
диаметр окружности равен диагонали квадрата
площадь ромба (квадрат является ромбом) — это полупроизведение его диагоналей
поэтому площадь квадрата равна половине квадрата диаметра окружности
Похожие вопросы
Квадрат вписанный в окружность

Обновлено 28.02.2022
Содержание
- Определение
- Формулы
- Радиус вписанной окружности в квадрат
- Радиус описанной окружности около квадрата
- Сторона квадрата
- Площадь квадрата
- Периметр квадрата
- Диагональ квадрата
- Свойства
Определение
Квадрат, вписанный в окружность — это квадрат, который находится
внутри окружности и соприкасается с ней углами.
На рисунке 1 изображена окружность, описанная около
квадрата и окружность, вписанная в квадрат.

Формулы
Радиус вписанной окружности в квадрат
- Радиус вписанной окружности в квадрат, если известна сторона:
[ r=frac{a}{2} ]
- Радиус вписанной окружности в квадрат, если известен периметр:
[ r=frac{P}{8} ]
- Радиус вписанной окружности в квадрат, если известна площадь:
[ r=frac{sqrt S}{2} ]
- Радиус вписанной окружности в квадрат, если известен радиус описанной окружности:
[ r=frac{ R}{sqrt 2} ]
- Радиус вписанной окружности в квадрат, если известна диагональ:
[ r=frac{ d}{2sqrt 2} ]
Радиус описанной окружности около квадрата
- Радиус описанной окружности около квадрата, если известна сторона:
[ R=afrac{sqrt 2}{ 2} ]
- Радиус описанной окружности около квадрата, если известен периметр:
[ R=frac{ P}{4 sqrt 2} ]
- Радиус описанной окружности около квадрата, если известна площадь:
[ R=frac{sqrt 2S}{ 2} ]
- Радиус описанной окружности около квадрата, если известен радиус вписанной окружности:
[ R= r sqrt2 ]
- Радиус описанной окружности около квадрата, если известна диагональ:
[ R=frac{d}{2} ]
Сторона квадрата
- Сторона квадрата вписанного в окружность, если известна площадь:
[ a=sqrt S ]
- Сторона квадрата вписанного в окружность, если известна диагональ:
[ a=frac{ d}{sqrt 2} ]
- Сторона квадрата вписанного в окружность, если известен периметр:
[ a=frac{ P}{4} ]
Площадь квадрата
- Площадь квадрата вписанного в окружность, если известна сторона:
[ S=a^2 ]
- Площадь квадрата вписанного в окружность, если известен радиус вписанной окружности:
[ S=4r^2 ]
- Площадь квадрата вписанного в окружность, если известен радиус описанной окружности:
[ S=2R^2 ]
- Площадь квадрата вписанного в окружность, если известен периметр:
[ S=frac{ P^2}{ 16} ]
- Площадь квадрата вписанного в окружность, если известна диагональ:
[ S=frac{ d^2}{ 2} ]
Периметр квадрата
- Периметр квадрата вписанного в окружность, если известна сторона:
[ P=4a ]
- Периметр квадрата вписанного в окружность, если известна площадь:
[ P=4sqrt S ]
- Периметр квадрата вписанного в окружность, если известен радиус вписанной окружности:
[ P=8r ]
- Периметр квадрата вписанного в окружность, если известен радиус описанной окружности:
[ P=4Rsqrt 2 ]
- Периметр квадрата вписанного в окружность, если известна диагональ:
[ P=2dsqrt 2 ]
Диагональ квадрата
- Диагональ квадрата вписанного в окружность, если известна сторона:
[ d=asqrt 2 ]
- Диагональ квадрата вписанного в окружность, если известна площадь:
[ d=sqrt 2S ]
- Диагональ квадрата вписанного в окружность, если известен периметр:
[ d=frac{ P}{2 sqrt 2} ]
- Диагональ квадрата вписанного в окружность, если известен радиус вписанной окружности:
[ d=2rsqrt 2 ]
- Диагональ квадрата вписанного в окружность, если известен радиус описанной окружности:
[ d=2R ]
Свойства
- Все углы в квадрате прямые.
- Все стороны квадрата равны.
- Сумма всех углов квадрата 360°.
- Диагонали квадрата одновременно равны, пересекаются под прямым углом и являются биссектрисами углов.
- Точка пересечения диагоналей квадрата является центром вписанной и описанной окружности.
- Диагонали квадрата перпендикулярны, точкой пересечения делятся пополам.
- Квадрат обладает симметрией.
Как найти площадь квадрата вписанного в круг
Как найти площадь квадрата, вписанного в круг! Как мы видим из ниже переведённого скрина, то диагональ квадрата равна диаметру круга!
О площади квадрата мы тоже говорили, и возьмем оттуда нашу формулу площади.
И собственно нам останется выразить сторону квадрат через диагональ!
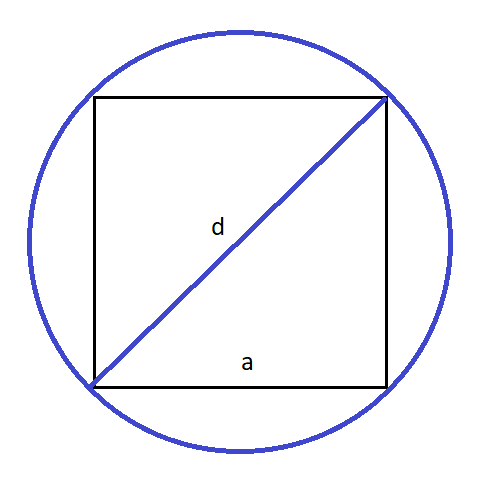
d² = а² + b² или для квадрата => d² = 2а²
Из этого неравенства надо вывести чему равна сторона а….
d² = 2а² => d²/2 = а² => а² = d²/2
Далее нам понадобится та площадь из верхней ссылки(площадь квадрата…) и в ней нам нужно заменить сторону в квадрате на верхнее выражение…
S = a²
и получим…
Чему рана площадь квадрата вписанного в круг
S = d²/2
Другими словами, площадь квадрата, вписанного в круг равна квадрату диагонали деланного на два!
Если вам нужно вывести данную формулу через радиус, то давайте сделаем это…
Как мы знаем, что диаметр равен двум радиусам:
d = 2R
Заменим верхнее в нижним и получим:
S = (2R)²/2 => S = (4R²)/2 => S = 2(R²/2)
Написать что-нибудь…
площадь круга вписанного в квадрат ,
найти площадь круга вписанного в квадрат ,
площадь квадрата вписанного в круг равна ,
площадь квадрата вписанного в круг ,
площадь квадрата вписанного в круг равна ,
формула площади круга вписанного в квадрат ,
