Как найти площадь вписанного в треугольник квадрата

Я пока вижу только два варианта вписывания квадрата в этот прямоугольный треугольник.

Первый вариант

Введём оротонормировнную систему координат и поместим C в её начало. Ось абсцисс пустим вдоль AC справа-налево, ось ординат направим просто вверх. Вектор B-C из условия имеет координаты (10; 6). Вектор p получается масштабированием вектора B-C, т.е., p=k(B-C) для некоторого k.

Выпишем координаты p=k(B-C)=(10k, 6k) по отдельности:

p_x=10k, (1)

p_y=6k. (2)

С другой стороны, понятно, что сторона квадрата равна p_y = A_x-p_x = 10-px. Подстановка в (2) даёт 6k = 10 – p_x, а подстановка (1) в получившееся выражение даёт 6k = 10 – 10k => k = 10/16.

Из (2), сторона квадрата теперь равна p_y=6*10/16, а искомая площадь квадрата равна квадрату этой стороны:

S_0 = (p_y)^2 = 3600/256 ~ 14 [кв.ед.].

Второй вариант

Система координат введена так же (см. выше). По рисунку видно, что вектор q может быть получен сложением векторов s, r-s и q-r:

q = s + (r-s) + (q-r). (3)

Также видно, что вектор q-r получается из r-s поворотом на прямой угол. Матрица поворота действуя на r-s просто меняет координаты местами и у одной координаты (в данном случае у абсциссы) меняет знак. Т.е.,

(q-r)_x = -(r-s)_y, (4)

(q-r)_y = (r-s)_x, (5)

где нижний индекс даёт проекцию на указанную ось (x — абсцисса, y — ордината).

Вектор q пропорционален вектору B:

q = h*(10,6) = (10h, 6h), (6)

для некоторого h.

Подставляя (4), (5) и (6) в (3) и записывая уравнение в скалярной форме, получаем систему:

s_x + r_x – s_x – r_y + s_y = 10h

s_y + r_y – s_y + r_x – s_x = 6h.

Приводя подобные слагаемые и подставляя известные значения s_y=0 и r_x=10, преобразуем эту систему в

r_y + 10 – s_x = 6h (7)

10 – r_y = 10h (8)

Из (8) выражаем h как h = (10-r_y)/10 и подставляем в (7), получая выражение s_x = r_y + 10 + 6(10-r_y)/10. Оно преобразуется в

s_x = 16r_y/10 + 4. (9)

Замечаем, что вектор r-s коллинеарен B и поэтому

r-s = kB, (10)

для некоторого k.

Скалярно: r_x – s_x = 10k, r_y – s_y = 6k. Отсюда сначала выражаем k как k=(10-s_x)/10, а потом r_y в виде

r_y = 6k = 6(10-s_x)/10. (11)

Подставляем (9) в (11) и приходим к

r_y = (6/10)(10 – 16r_y/10 – r) =

= (6/10)(6 – 16r_y/10) =

= 36/10 – 96r_y/100 =>

=> r_y = 36*100/(10*196) = 90/49.

Подстановка в (11) даёт k = r_y/6 = 90/(49*6) = 15/49. Подстановка в (10) даёт r-s = 15B/49. Длина равна |r-s|=15|B|/49. Искомая площадь квадрата со стороной на этом векторе равна квадрату его длины, т.е.,

S_1 = |r-s|^2 = (15^2)*|B|^2/(49^2) =

= (15^2)*(10^2 + 6^2)/(49^2) =

= (15^2)*136/(49^2) = 225*136/(49^2) =

= 30600/2401 = 12 + 1788/2401 ~ 12,7 [кв.ед.].

Ну вот такие вот площади получились: S_0 ~ 14 [кв.ед.], S_1 ~ 12,7 [кв.ед.].

Решение

Пусть — угол треугольника, противолежащий катету, равному a; x — сторона квадрата. Тогда

xtg + xctg + x = , tg = .

Следовательно,

x = = .

Ответ

.

Сегодня задачка на логику и геометрию, как в школе. Это не нужно в ИТ, но иногда нужно отвлекаться. 

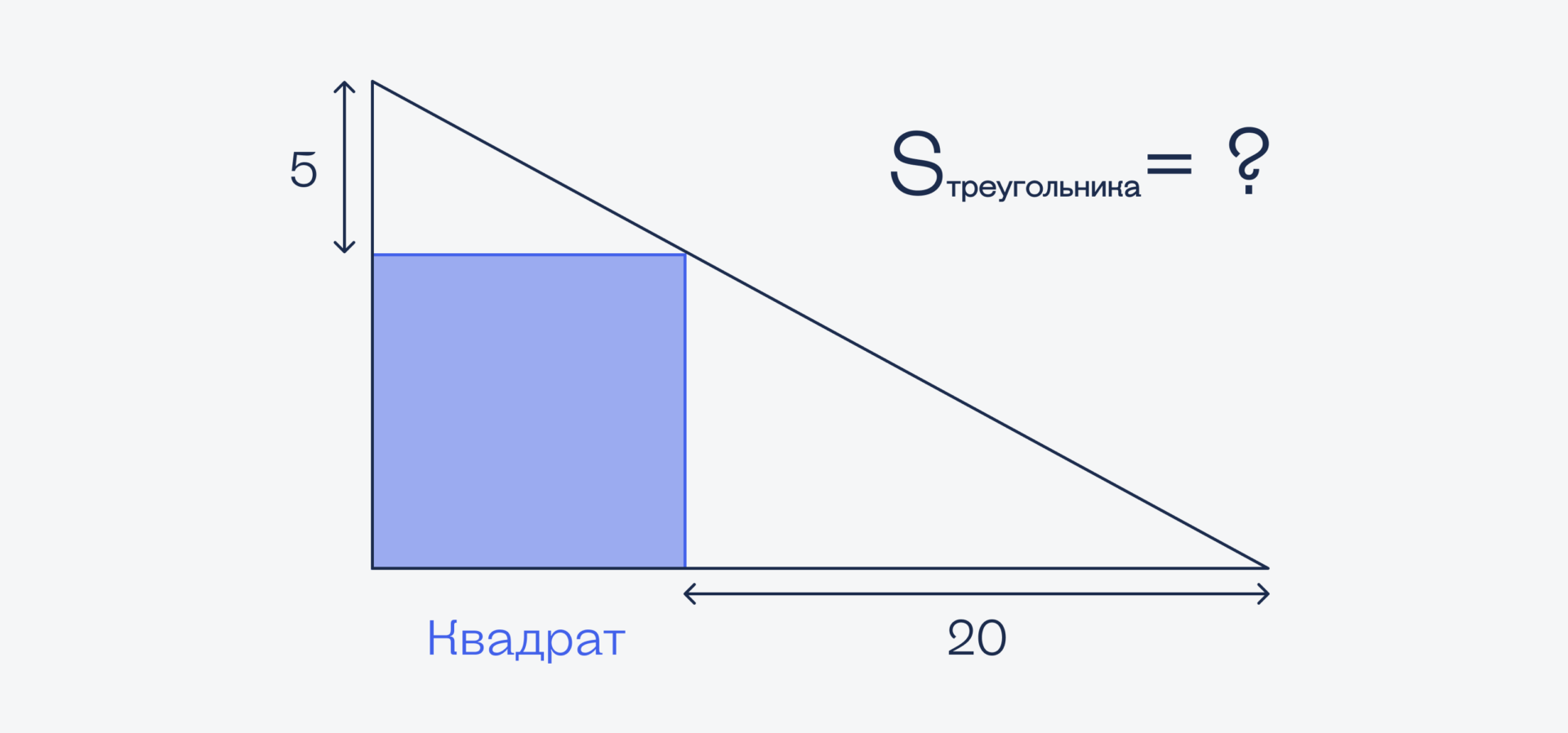
Вот картинка, тут всё понятно. Нужно найти площадь треугольника:

Решение с тригонометрией

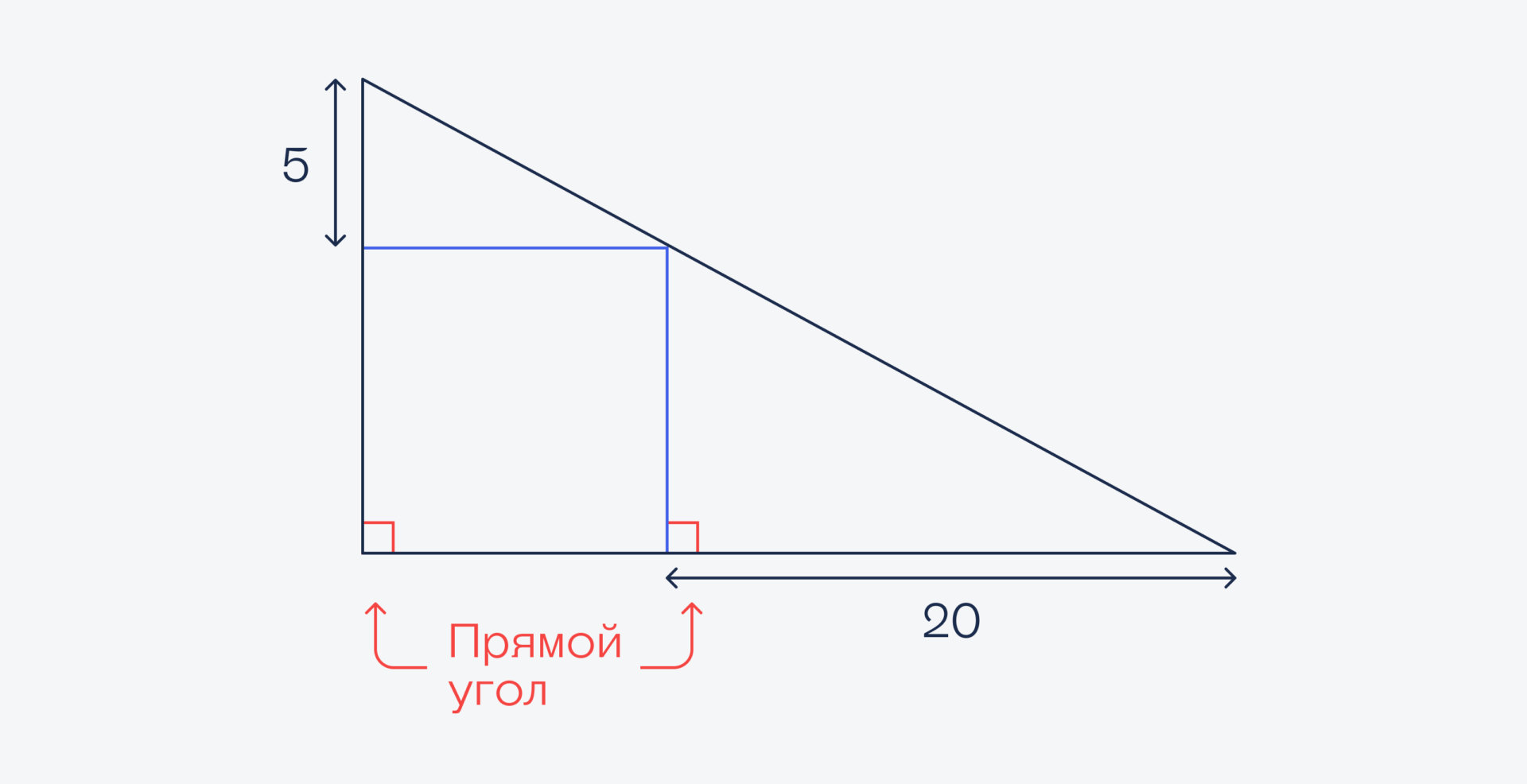
Так как у нас в треугольник вписан квадрат, это значит, что обе его стороны находятся под прямым углом к основанию треугольника:

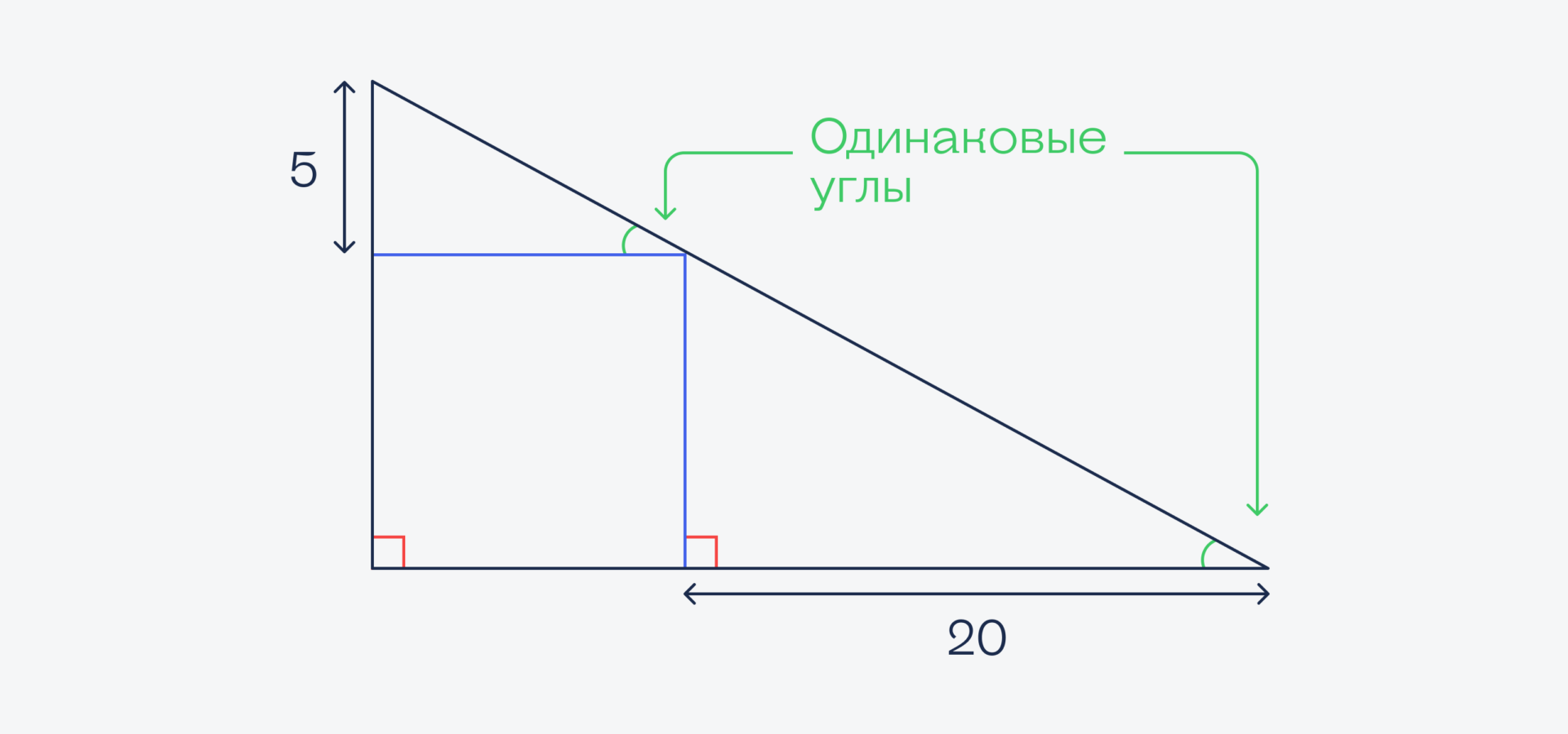
А раз так, то угол, который образуется при пересечении наклонной линии, совпадает с углом наклона этой линии к основанию:

Если у треугольников есть два одинаковых угла, то такие треугольники называются подобными. А раз они подобные, то и соотношение сторон у них будет одно и то же. Обозначим сторону квадрата за X:

Теперь построим соотношение:

5 / X = X / 20 ← решим это уравнение

X² = 5 × 20 = 100

X = 10

Зная сторону квадрата, можно легко найти площадь всего треугольника:

(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 225

Нестандартное решение без тригонометрии

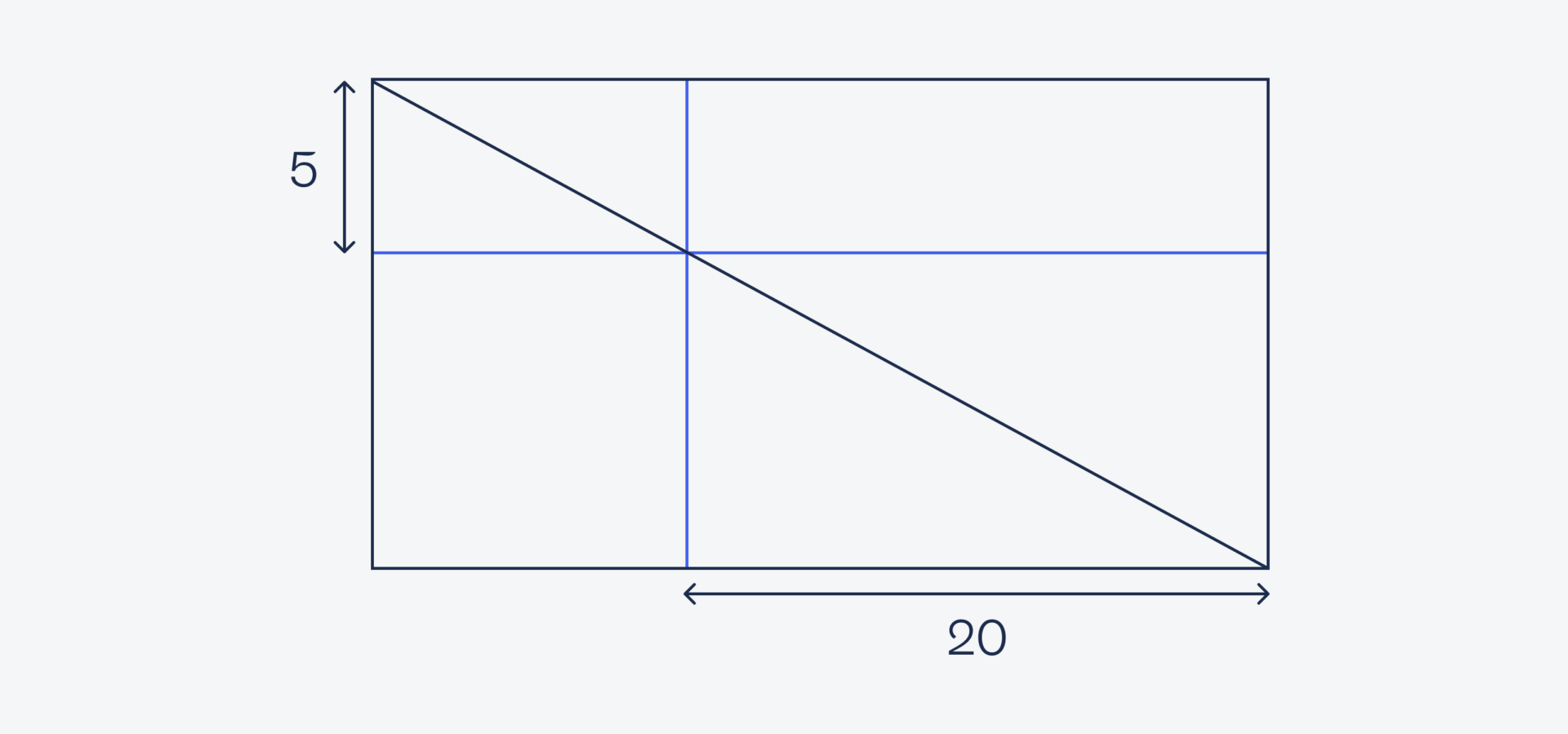
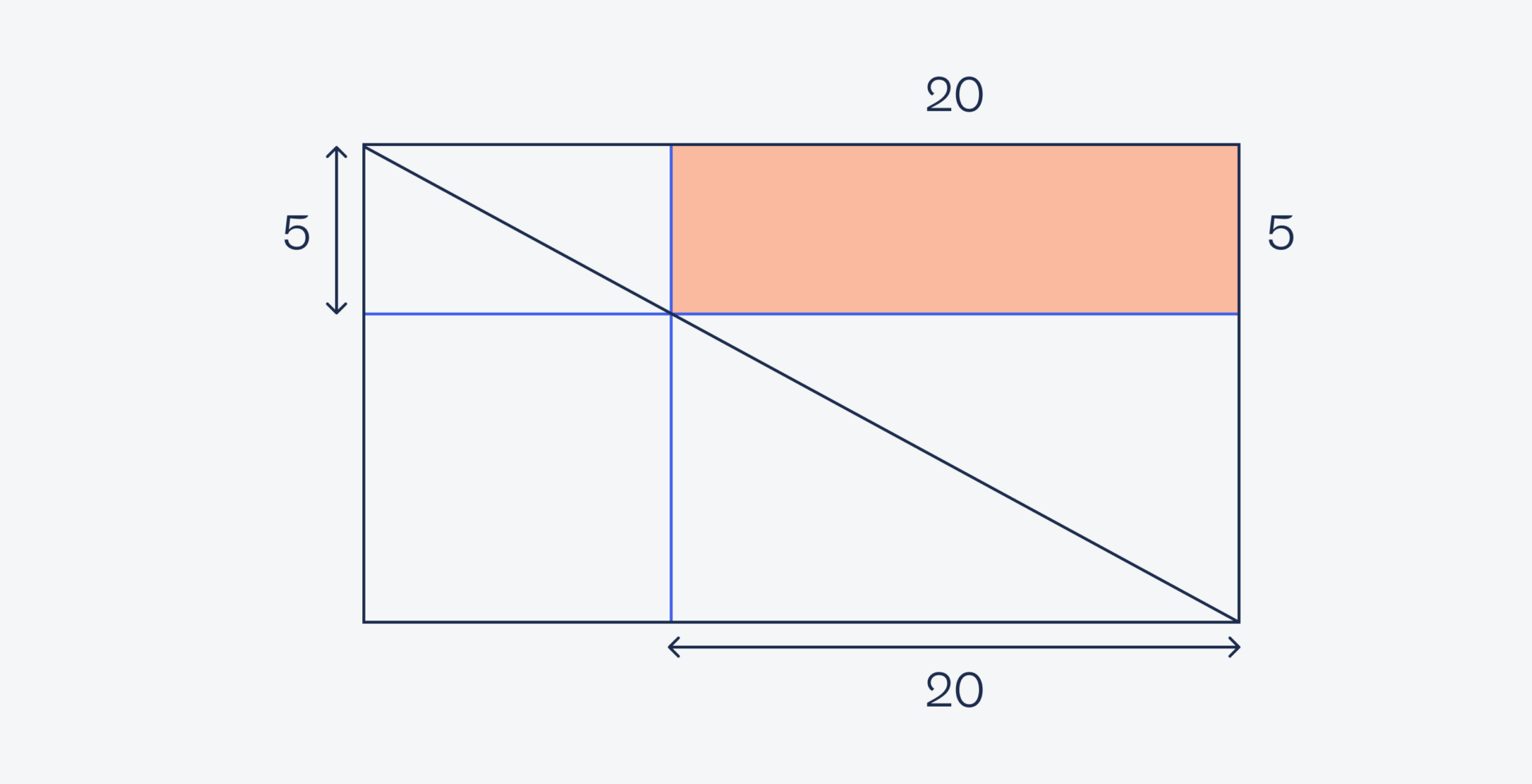
Представим, что мы ничего не знаем про тригонометрию, углы и подобие треугольников. Возьмём наш рисунок и мысленно достроим его до прямоугольника:

Так как у квадрата все углы прямые, то и синие линии у нас тоже пересекаются под прямыми углами между собой и с внешним прямоугольником. Это значит, что мы можем перенести известные размеры на оранжевый прямоугольник:

Зная длину и ширину, посчитаем его площадь — 5 × 20 = 100.

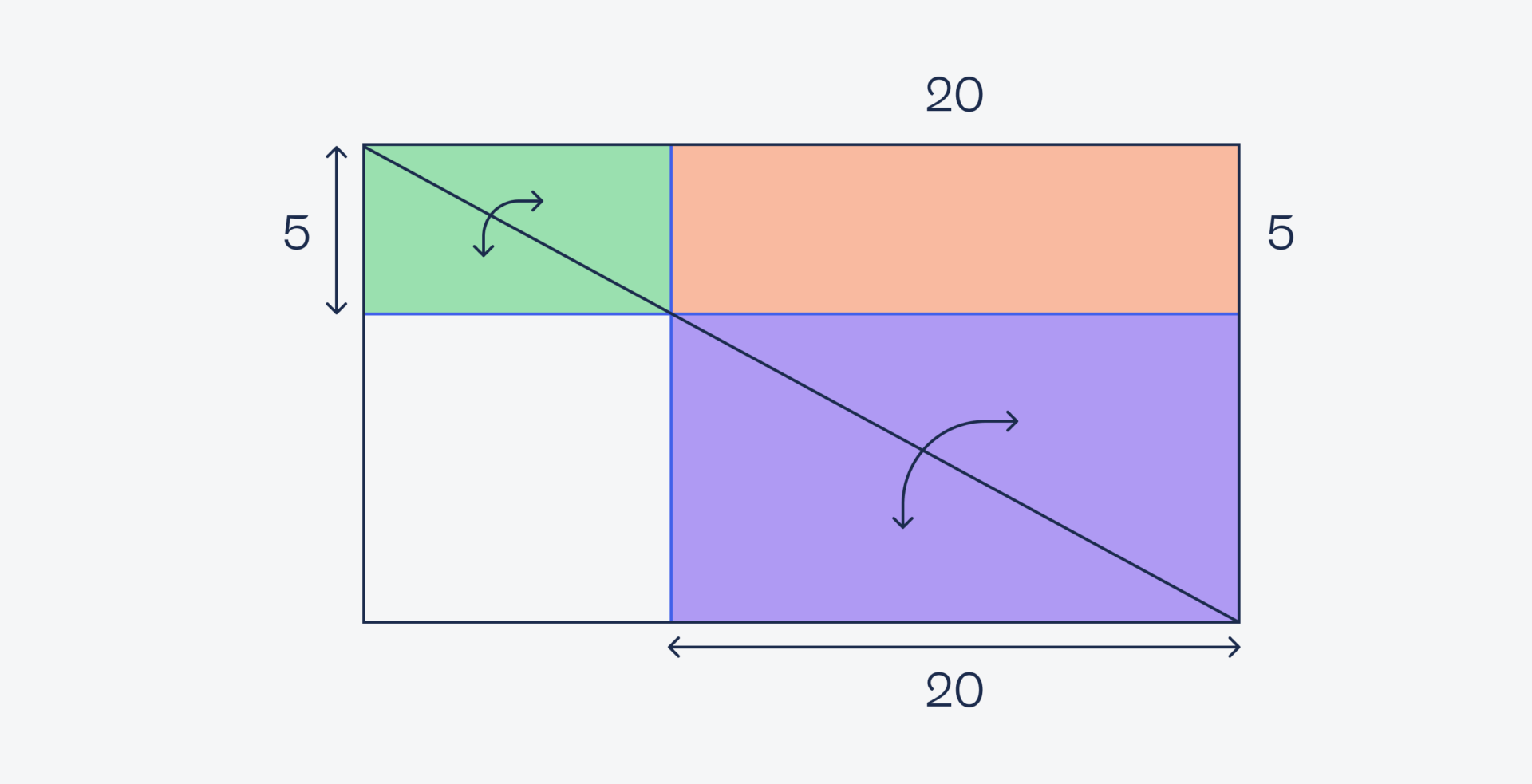
Теперь посмотрим на рисунок так: у нас есть прямоугольник, разделённый пополам по диагонали. Это значит, что площадь нижних треугольников совпадает с площадью верхних треугольников:

Но раз у нас часть площадей в верхнем и нижнем треугольнике одинаковая, их можно вычесть из обеих частей:

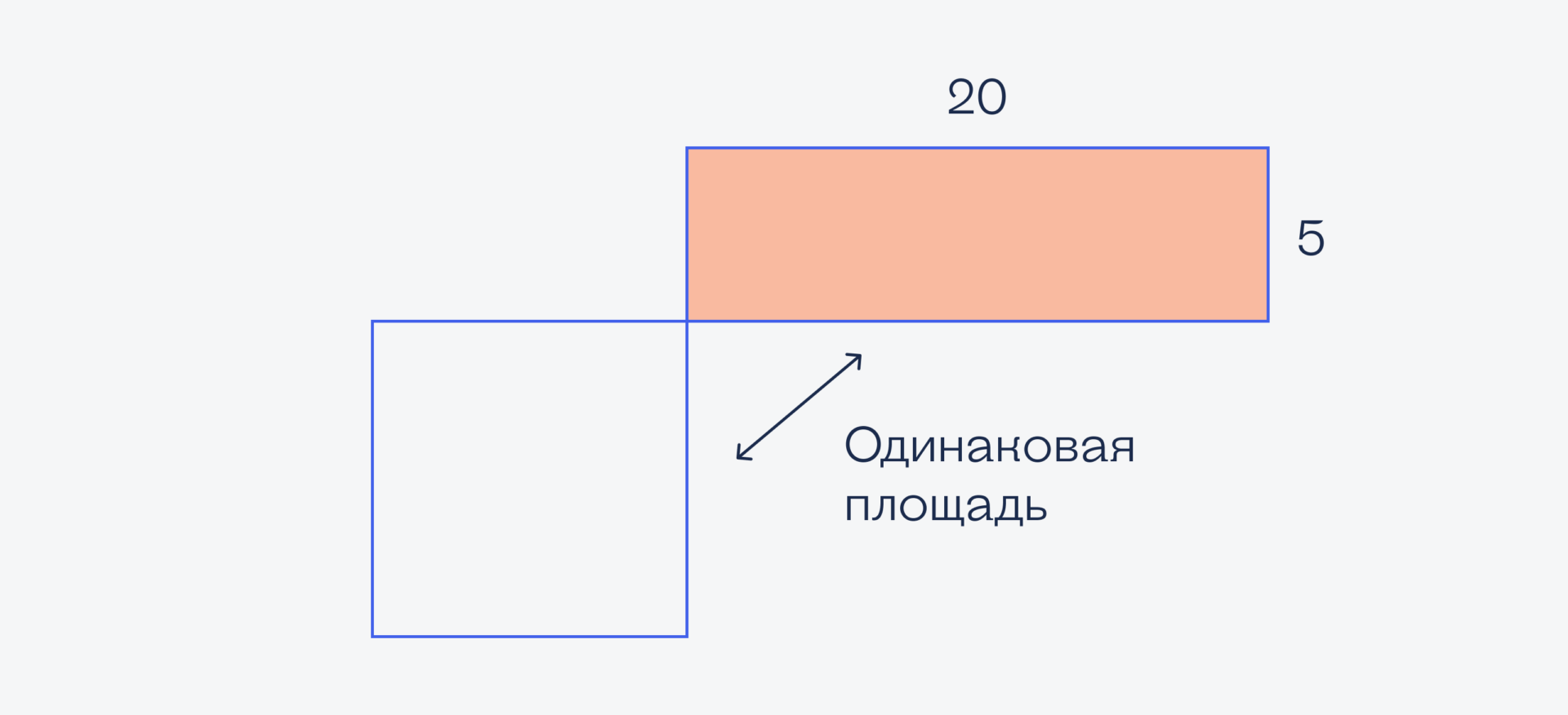
Получается, что площадь оранжевого прямоугольника совпадает с площадью квадрата. А мы знаем, что площадь прямоугольника равна 100; получается, чтобы найти сторону квадрата, нужно извлечь квадратный корень:

√100 = 10

Значит, сторона квадрата равна 10. Этого достаточно, чтобы посчитать всю площадь треугольника:

(5 + 10) × (10 + 20) / 2 = 15 × 30 / 2 = 255