Чтобы найти площадь поверхности цилиндра необходимо знать радиус его основания и высоту. Очень важно понимать, что существует две поверхности – боковая и полная. Площадь боковой поверхности включает в себя площадь поверхности цилиндра без учета площади его оснований. Полная же площадь основания цилиндра включает как площадь боковой поверхности, так и обоих оснований цилиндра.
На нашем сайте вы можете рассчитать и объем цилиндра
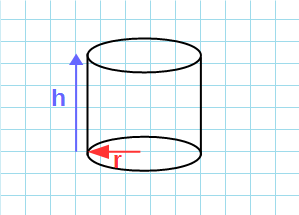
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые её пересекают.
Содержание:
- калькулятор площади поверхности цилиндра
- формула площади поверхности цилиндра
- формула площади боковой поверхности цилиндра
- примеры задач
Формула площади поверхности цилиндра
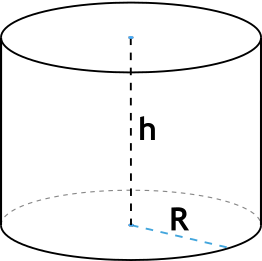
{S_{полн} = 2pi R(h+R)}
R – радиус основания цилиндра
h – высота цилиндра
Формула площади боковой поверхности цилиндра
{S_{бок} = 2pi Rh}
R – радиус основания цилиндра
h – высота цилиндра
Примеры задач на нахождение площади поверхности цилиндра
Задача 1
Найдите площадь поверхности цилиндра если его высота равна 5см а радиус 6см.
Решение
Так как необходимо найти площадь полной поверхности цилиндра, воспользуемся первой формулой. Подставим в нее значения из условия и произведем вычисления.
S_{полн} = 2pi R(h+R) = 2pi cdot 6(5+6) = 12pi cdot 11 = 132 pi : см^2 approx 414.69023 : см^2
Ответ: 132 pi : см^2 approx 414.69023 : см^2
Чтобы проверить правильность ответа можно использовать калькулятор .
Задача 2
Найдите площадь боковой поверхности цилиндра, если радиус основания равен 2см а высота 7см.
Решение
Для решения этой задачи нам потребуется вторая формула.
S_{бок} = 2pi Rh = 2pi cdot 2 cdot 7 = 28 pi : см^2 approx 87.96459 : см^2
Ответ: 28 pi : см^2 approx 87.96459 : см^2
Осталось убедиться, что задача решена верно, для этого используем калькулятор .
В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
Площадь поверхности цилиндра
4.6
Средняя оценка: 4.6
Всего получено оценок: 9395.
4.6
Средняя оценка: 4.6
Всего получено оценок: 9395.
Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.
Опыт работы учителем математики – более 33 лет.
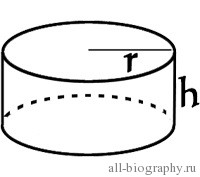У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.
Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.
Известно, что площадь окружности равна πr2. Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr2 + πr2 = 2πr2.
Боковая поверхность цилиндра
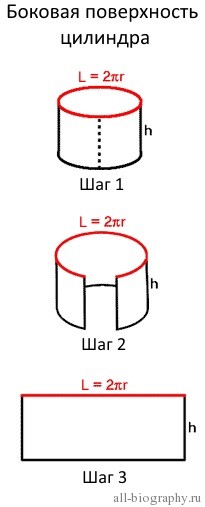Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.
Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.
Формула площади боковой поверхности цилиндра
Sбок. = 2πrh
r – радиус цилиндра, h – высота цилиндра
Площадь полной поверхности цилиндра
Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).
Формула площади полной поверхности цилиндра
S = 2πr2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра
Примеры расчета площади поверхности цилиндра
Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.
1. Радиус основания цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.
Площадь боковой поверхности рассчитывается по формуле: Sбок. = 2πrh
Sбок. = 2 * 3,14 * 2 * 3
Sбок. = 6,28 * 6
Sбок. = 37,68
Площадь боковой поверхности цилиндра равна 37,68.
2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?
Площадь полной поверхности рассчитывается по формуле: S = 2πr2 + 2πrh
S = 2 * 3,14 * 62 + 2 * 3,14 * 6 * 4
S = 2 * 3,14 * 36 + 2 * 3,14 * 24
S = 226,08 + 150,72
S = 376,8
Площадь поверхности цилиндра равна 376,8.
3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.
Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:
h = Sбок./2πr
Значение радиуса получаем из формулы: d = 2r
h = 24π / (2π * 0,5d)
h = 24π / (2π * 0,5 * 3)
h = 12 / 1,5
h = 8
Высота цилиндра равна 8.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Dark Spyro
5/5
-
Татьяна Матвиенко
5/5
-
Юрий Евдокимов
5/5
-
Михаил Чепурной
5/5
-
Дмитрий Новиков
5/5
-
Дилноза Саипова
4/5
-
Darya Simonova
5/5
-
Тамара Иванова
5/5
-
Татьяна Немчинова
5/5
-
Рамиль Сагиров
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 9395.
А какая ваша оценка?
Как рассчитать площадь цилиндра
На данной странице калькулятор поможет рассчитать площадь поверхности цилиндра онлайн. Для расчета задайте высоту и радиус.
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Боковая поверхность
Формула площадь боковой поверхности цилиндра через высоту и радиус:
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
Полная поверхность
Формула площадь полной поверхности цилиндра через высоту и радиус:
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
Цилиндр — геометрическое тело, которое можно получить при вращении прямоугольника вокруг какой-либо его стороны.
Онлайн-калькулятор площади поверхности цилиндра
На самом деле, это определение только самого простого, кругового цилиндра. Более общее определение цилиндрического тела следующее:
Цилиндром называют тело, образованное пересечением параллельных друг другу прямых и двух плоских поверхностей.
Такие прямые называются образующими данного цилиндра.
Прямая, перпендикулярная обоим основаниям, является высотой цилиндра.
Плоские поверхности называют основаниями данного цилиндра. Часто, они параллельны друг другу, но не всегда.
Виды цилиндра
Виды цилиндра зависят от того, под каким углом пересекаются образующие и основания нашего тела.
Если угол равен 90 градусам, то получим, так называемый, прямой цилиндр. У него есть ось симметрии – это перпендикуляр, соединяющий центры его оснований.
Если угол другой, то цилиндр называется наклонным.
Если форма основания – гипербола, то цилиндр гиперболический, если парабола — параболический, если эллипс — эллиптический, если круг — круговой.
Если основания цилиндра не параллельны, то он называется косым.
Формула площади поверхности цилиндра
Полная площадь поверхности цилиндра является суммой его боковой площади поверхности и площади оснований.
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}
SоснS_{text{осн}} — площадь оснований;
SбокS_{text{бок}} — площадь боковой поверхности.
При вычислении площади поверхности цилиндра важным фактором является вид цилиндра. От него зависит и конкретная формула для площади.
Формула площади поверхности кругового цилиндра
Sосн=2⋅π⋅r2S_{text{осн}}=2cdotpicdot r^2
Sбок=2⋅π⋅r⋅hS_{text{бок}}=2cdotpicdot rcdot h
rr — радиус круга (основания кругового цилиндра);
hh — высота этого цилиндра.
Сокращенно, это формулу можно записать так:
S=Sосн+Sбок=2⋅π⋅r2+2⋅π⋅r⋅h=2⋅π⋅r⋅(r+h)S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+2cdotpicdot rcdot h=2cdotpicdot rcdot(r+h)
Радиус круга, лежащего в основании прямого кругового цилиндра, имеет длину 6 (см.). Высота цилиндра – 20 (см.). Найдите полную площадь его поверхности.
Решение:
r=6r=6
h=20h=20
По формуле:
S=2⋅π⋅r⋅(r+h)=2⋅π⋅6⋅(6+20)≈979,68S=2cdotpicdot rcdot(r+h)=2cdotpicdot 6cdot(6+20)approx979,68 (см. кв.)
Ответ: 979,68 см. кв.
Формула площади поверхности наклонного кругового цилиндра
Sосн=2⋅π⋅r2S_{text{осн}}=2cdotpicdot r^2
Sбок=p⋅lS_{text{бок}}=pcdot l
rr — радиус круга (основания кругового цилиндра);
pp — периметр сечения наклонного цилиндра перпендикулярно образующей;
ll — длина образующей этого цилиндра.
Найти площадь поверхности наклонного цилиндра, если периметр pp сечения плоскости, составляющей прямой угол с образующей, равен 30 (см.), а сама образующая равна 7 (см.) Радиус окружности, лежащей в основе цилиндра в два раза меньше его образующей.
Решение:
r=l2r=frac{l}{2}
p=30p=30
l=7l=7
Найдем сначала радиус основания:
r=l2=72=3.5r=frac{l}{2}=frac{7}{2}=3.5
Тогда полная площадь:
S=Sосн+Sбок=2⋅π⋅r2+p⋅l=2⋅π⋅3.52+30⋅7≈76,93+210=286,93S=S_{text{осн}}+S_{text{бок}}=2cdotpicdot r^2+pcdot l=2cdotpicdot 3.5^2+30cdot 7approx76,93+210=286,93 (см. кв.)
Ответ: 286,93 см. кв.
На сайте Студворк предусмотрено решение контрольных работ на заказ для школьников и студентов.
