Как найти площадь всей поверхности икосаэдра

Запрос «Икосаэдр» перенаправляется сюда; см. также другие значения.

Правильный икосаэдр

(вращающаяся модель)

Тип

правильный многогранник

Комбинаторика

Элементы

20 граней
30 рёбер
12 вершин

Χ = 2

Грани

правильные треугольники

Конфигурация вершины

3.3.3.3.3

Двойственный многогранник

правильный додекаэдр

Вершинная фигура

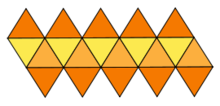
Развёртка

Классификация

Обозначения

Символ Шлефли

{3,5}

Символ Витхоффа^[en]

5 | 2 3

Диаграмма Дынкина

Группа симметрии

${displaystyle I_{h}}$

Группа вращения

Количественные данные

Длина ребра

Площадь поверхности

${displaystyle 5a^{2}{sqrt {3}}}$

Объём

${displaystyle {begin{matrix}{5 over 12}end{matrix}}(3+{sqrt {5}})a^{3}}$

Двугранный угол

${displaystyle arccos left(-{frac {sqrt {5}}{3}}right)approx 138.19^{circ }}$

Телесный угол при вершине

${displaystyle 2pi -5arcsin left({frac {2}{3}}right)}$

ср

Медиафайлы на Викискладе

Икосаэдр и его описанная сфера

Правильный икосаэдр, вписанный в сферу. Видно, что его вершины лежат в четырёх параллельных плоскостях, как доказал Папп Александрийский

Пра́вильный икоса́эдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сиденье», «основание») — правильный выпуклый многогранник, двадцатигранник^[1], одно из платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12.
Икосаэдр имеет 59 звёздчатых форм.

История[править | править код]

Евклид в предложении 16 книги XIII «Начал» занимается построением икосаэдра, получая сначала два правильных пятиугольника, лежащих в двух параллельных плоскостях — из десяти его вершин, и затем — две оставшиеся противоположные друг другу вершины^[2]^[3]^:127-131. Папп Александрийский в «Математическом собрании» занимается построением икосаэдра, вписанного в данную сферу, попутно доказывая, что двенадцать его вершин лежат в четырёх параллельных плоскостях, образуя в них четыре правильных треугольника^[3]^:315-316^[4].

Основные формулы[править | править код]

Площадь поверхности S, объём V правильного икосаэдра с длиной ребра a, а также радиусы вписанной и описанной сфер вычисляются по формулам:

Площадь:

$S=5a^{2}{sqrt 3}$

Объём:

$V={begin{matrix}{5 over 12}end{matrix}}(3+{sqrt 5})a^{3}$

Радиус вписанной сферы^[5]:

Радиус полувписанной сферы равен ${displaystyle {frac {1}{2}}{sqrt {frac {3+{sqrt {5}}}{2}}}aapprox 0{,}809a.}$ ^[5]

Радиус описанной сферы^[5]:

Свойства[править | править код]

Двугранный угол между любыми двумя смежными гранями правильного икосаэдра равен arccos(−^√5⁄₃) = 138,189685°.
Все двенадцать вершин правильного икосаэдра лежат по три в четырёх параллельных плоскостях, образуя в каждой из них правильный треугольник.
Десять вершин правильного икосаэдра лежат в двух параллельных плоскостях, образуя в них два правильных пятиугольника, а остальные две — противоположны друг другу и лежат на двух концах диаметра описанной сферы, перпендикулярного этим плоскостям. Расстояние между симметричными парами вышеупомянутых плоскостей, образованных пятью вершинами равно радиусу круга описываемого вокруг этого пятиугольника (это правило позволяет довольно легко создать 3D-модель правильного икосаэдра).
Угол между двумя соседними вершинами относительно центра тела правильного икосаэдра называют икосаэдральным углом. Он равен арккотангенсу ¹⁄₂ (arcctg ¹⁄₂ ≈ 63,434949°), или углу между диагональю и меньшей стороной прямоугольника, у которого отношение сторон равно 1:2.
Правильный икосаэдр можно вписать в куб, при этом шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба.
В правильный икосаэдр может быть вписан правильный тетраэдр так, что четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра.
Правильный икосаэдр и правильный додекаэдр являются двойственными многогранниками:
- Правильный икосаэдр можно вписать в правильный додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра.
- В правильный икосаэдр можно вписать правильный додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра.
Собрать модель правильного икосаэдра можно при помощи 20 равносторонних треугольников.
Невозможно собрать правильный икосаэдр из правильных тетраэдров, так как радиус сферы, описанной вокруг икосаэдра, соответственно и длина бокового ребра (от вершины до центра такой сборки) тетраэдра меньше ребра самого икосаэдра. Правильный икосаэдр можно разбить на 20 тетраэдров, соединив вершины икосаэдра с его центром, но эти тетраэдры не являются правильными — угол между их рёбрами при вершине, совпадающей с центром икосаэдра, равен икосаэдральному углу (≈63,434949°), а не 60°, как у правильного тетраэдра.

Усечённый икосаэдр[править | править код]

Усечённый икосаэдр — многогранник, состоящий из 12 правильных пятиугольников и 20 правильных шестиугольников. Имеет икосаэдрический тип симметрии. По сути классический футбольный мяч имеет форму не шара, а усечённого икосаэдра с выпуклыми (сферическими) гранями.

Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90.

В мире[править | править код]

Икосаэдр лучше всего из всех правильных многогранников подходит для триангуляции сферы методом рекурсивного разбиения^[6]. Поскольку он содержит наибольшее среди них количество граней, искажение получающихся треугольников по отношению к правильным минимально.
Икосаэдр применяется как игральная кость в настольных ролевых играх, и обозначается при этом d20 (dice — кости).

Тела в виде икосаэдра[править | править код]

Капсиды многих вирусов (например, бактериофаги, мимивирус).

См. также[править | править код]

Звёздчатый многогранник

Примечания[править | править код]

↑ Селиванов Д. Ф.,. Тело геометрическое // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
↑ Euclid’s Elements, Book XIII, Proposition 16. Дата обращения: 3 сентября 2014. Архивировано 30 августа 2014 года.
↑ ¹ ² Начала Евклида. Книги XI—XV. — М.—Л.: Государственное издательство технико-теоретической литературы, 1950. — Помимо перевода на русский язык сочинения Евклида это издание в комментариях содержит перевод предложений Паппа о правильных многогранниках.
↑ Оригинальный текст на древнегреческом языке с параллельным переводом на латинский язык: Pappi Alexandrini Collectionis. — 1876. — Vol. I. — P. 150—157.
↑ ¹ ² ³ Доказательство приведено в: Cobb, John W. The Icosahedron (англ.) (май 2007). Дата обращения: 3 сентября 2014. Архивировано 4 мая 2016 года.
↑ OpenGL Red Book Ch.2 Архивировано 8 января 2015 года.

Литература[править | править код]

Клейн Ф. Лекции об икосаэдре и решение уравнений пятой степени / Ф. Клейн; пер. с нем. А. Л. Городенцев, А. А. Кириллов, ред. А. Н. Тюрин. — М.: Наука, 1989. — 332 с. — ISBN 5020141976.

Источник

Икосаэдр.

Икосаэдр – один из пяти типов правильных многогранников, имеет 20 граней (треугольных), 30 ребер, 12 вершин (в каждой вершине сходятся 5 ребер).

Икосаэдр, как правильный многогранник

Основные формулы икосаэдра

Свойства икосаэдра

Икосаэдр, как правильный многогранник:

Икосаэдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сиденье», «основание») – один из пяти типов правильных многогранников, имеет 20 граней (треугольных), 30 ребер, 12 вершин (в каждой вершине сходятся 5 ребер).

Если а – длина ребра икосаэдра, то его объем V = 5/12 · a³· (3+5^1/2) ≈ 2,1817 · a³.

Икосаэдр имеет 59 звездчатых форм.

Вершины вписанного икосаэдра лежат в четырёх параллельных плоскостях.

Основные формулы икосаэдра:

Площадь поверхности S, объём V икосаэдра с длиной ребра a, а также радиусы вписанной и описанной сфер вычисляются по формулам:

Площадь поверхности икосаэдра: S = 5 · a²· 3^1/2.

Объём икосаэдра: V = 5/12 · a³ · (3+5^1/2).

Радиус вписанной сферы икосаэдра: R = 1/12 · (42+18 · (5·а)^1/2)^1/2 = 1/4 · 3^1/2 · (3+5^1/2) · а.

Радиус описанной сферы икосаэдра: R = 1/4 · (2 · (5+5^1/2))^1/2 · a.

Свойства икосаэдра:

– двугранный угол между любыми двумя смежными гранями икосаэдра равен arccos(-√5/3) = 138,189685°;

– телесный угол при вершине икосаэдра равен 2·π – 5·arcsin(2/3) ≈ 2,63455 cp (стерадиан);

– все двенадцать вершин икосаэдра лежат по три в четырёх параллельных плоскостях, образуя в каждой из них правильный треугольник;

– десять вершин икосаэдра лежат в двух параллельных плоскостях, образуя в них два правильных пятиугольника, а остальные две — противоположны друг другу и лежат на двух концах диаметра описанной сферы, перпендикулярного этим плоскостям;

– икосаэдр можно вписать в куб, при этом шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба;

– в икосаэдр может быть вписан тетраэдр, так что четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра;

– икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра;

– в икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра;

– усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90;

– собрать модель икосаэдра можно при помощи 20 равносторонних треугольников;

– невозможно собрать икосаэдр из правильных тетраэдров, так как радиус описанной сферы вокруг икосаэдра, соответственно и длина бокового ребра (от вершины до центра такой сборки) тетраэдра меньше ребра самого икосаэдра.

Источник: https://ru.wikipedia.org/wiki/Правильный_икосаэдр

Примечание: © Фото //www.pexels.com, //pixabay.com

Коэффициент востребованности
2 857

Источник

Общая площадь поверхности икосаэдра Калькулятор

Search
Дом	математика ↺
математика	Геометрия ↺
Геометрия	3D геометрия ↺
3D геометрия	Платоновы тела ↺
Платоновы тела	Икосаэдр ↺
Икосаэдр	Площадь поверхности икосаэдра ↺
Площадь поверхности икосаэдра	Общая площадь поверхности икосаэдра ↺

✖Длина ребра икосаэдра — это длина любого из ребер икосаэдра или расстояние между любой парой смежных вершин икосаэдра.ⓘ Длина ребра икосаэдра [l_e]

+10%

-10%

✖Общая площадь поверхности икосаэдра – это общее количество плоскостей, заключенных во всей поверхности икосаэдра.ⓘ Общая площадь поверхности икосаэдра [TSA]

⎘ копия

Общая площадь поверхности икосаэдра Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Длина ребра икосаэдра: 10 метр –> 10 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

866.025403784439 Квадратный метр –> Конверсия не требуется

12 Общая площадь поверхности икосаэдра Калькуляторы

10+ Площадь поверхности икосаэдра Калькуляторы

Общая площадь поверхности икосаэдра формула

Общая площадь поверхности икосаэдра = 5*sqrt(3)*Длина ребра икосаэдра^2

TSA = 5*sqrt(3)*l_e^2

Что такое икосаэдр?

Икосаэдр представляет собой симметричную и замкнутую трехмерную форму с 20 одинаковыми равносторонними треугольными гранями. Это платоново тело, имеющее 20 граней, 12 вершин и 30 ребер. В каждой вершине встречаются пять равносторонних треугольных граней, а на каждом ребре встречаются две равносторонние треугольные грани.

Что такое Платоновые тела?

В трехмерном пространстве Платоново тело представляет собой правильный выпуклый многогранник. Он строится из конгруэнтных (одинаковых по форме и размеру), правильных (все углы равны и все стороны равны) многоугольных граней с одинаковым числом граней, сходящихся в каждой вершине. Пять тел, отвечающих этому критерию, — это тетраэдр {3,3}, куб {4,3}, октаэдр {3,4}, додекаэдр {5,3}, икосаэдр {3,5}; где в {p, q} p представляет количество ребер на грани, а q представляет количество ребер, встречающихся в вершине; {p, q} — символ Шлефли.

Источник

Вы здесь:

Главная
Икосаэдр

Икосаэдр

Древние греки дали многограннику имя по числу граней. «Икоси» означает двадцать, «хедра» – означает грань (Икосаэдр – двадцатигранник).

Поэтому на вопрос – “что такое икосаэдр?”, можно дать следующее определение: “Икосаэдр это геометрическое тело из двадцати граней, каждая их которых – правильный треугольник“.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел.
Икосаэдр имеет следующие характеристики:

Тип грани – правильный треугольник;
Число сторон у грани – 3;
Общее число граней – 20;
Число рёбер, примыкающих к вершине – 5;
Общее число вершин – 12;
Общее число рёбер – 30.

Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300° (60° x 5).
Икосаэдр имеет центр симметрии – центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.

Математические характеристики икосаэдра

Икосаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы икосаэдра

где a – длина стороны.

Сфера может быть вписана внутрь икосаэдра.

Радиус вписанной сферы икосаэдра

Для наглядности площадь поверхности икосаэдра можно представить в виде площади развёртки.

Площадь поверхности можно определить как площадь одной из сторон икосаэдра (это площадь правильного треугольника) умноженной на 20. Либо воспользоваться формулой:

Объем икосаэдра определяется по следующей формуле:

Правильные многогранники

Существует всего пять правильных многогранников:

Тетраэдр
Куб (Гексаэдр)
Октаэдр
Икосаэдр
Додекаэдр

Если какое-то из этих названий звучит для тебя как древний эльфийский язык, обязательно прочитай эту статью!

Давай посмотрим, как они выглядят, и разберем основные формулы – площади поверхности, объема, радиусов вписанной и описанной сферы.

А также решим задачу №8.

О том, как рисовать пространственные фигуры на плоскости, можно прочитать в нашей статье: «Изображение пространственных фигур. Визуальный гид».

Поехали!

Правильные многогранники — подробнее

Многогранник называется правильным, если:

он выпуклый;
все его грани являются правильными многоугольниками;
в каждой его вершине сходится одинаковое число его ребер.

Пять правильных многогранников

Тетраэдр

Тетраэдр состоит из четырёх равносторонних треугольников.

Фигура имеет 4 грани, 4 вершины и 6 ребер(a).

Площадь поверхности тетраэдра:

( displaystyle S={{a}^{2}}sqrt{3})

Объем тетраэдра:

( displaystyle V=frac{{{a}^{3}}}{12}sqrt{2})

Радиус описанной вокруг тетраэдра сферы:

( displaystyle R=frac{a}{4}sqrt{6})

Радиус вписанной в тетраэдр сферы:

( displaystyle R=frac{a}{12}sqrt{6})

Куб (Гексаэдр)

Куб состоит из шести квадратов.

Фигура имеет 6 граней, 8 вершин и 12 ребер (a).

Площадь поверхности куба:

( displaystyle S=6{{a}^{2}})

Объем куба:

( displaystyle V={{a}^{3}})

Радиус описанной вокруг куба сферы:

( displaystyle R=frac{a}{2}sqrt{3})

Радиус вписанной в куб сферы:

( displaystyle r=frac{a}{2})

Октаэдр

Октаэдр составлен из восьми равносторонних треугольников.

Фигура имеет 8 граней, 6 вершин и 12 ребер (a).

Площадь поверхности октаэдра:

( displaystyle S=2{{a}^{2}}sqrt{3})

Объем октаэдра:

( displaystyle V=frac{{{a}^{3}}}{3}sqrt{2})

Радиус описанной вокруг октаэдра сферы:

( displaystyle R=frac{a}{2}sqrt{2})

Радиус вписанной в октаэдр сферы:

( displaystyle r=frac{a}{6}sqrt{6})

Икосаэдр

Икосаэдр составлен из двадцати равносторонних треугольников.

Фигура имеет 20 граней, 12 вершин и 30 ребер (a).

Площадь поверхности икосаэдра:

( displaystyle S=5{{a}^{2}}sqrt{3})

Объем икосаэдра:

( displaystyle V=frac{5{{a}^{3}}}{12}left( 3+sqrt{5} right))

Радиус описанной вокруг икосаэдра сферы:

( displaystyle R=frac{a}{4}sqrt{2left( 5+sqrt{5} right)})

Радиус вписанной в икосаэдр сферы:

( displaystyle r=frac{a}{4sqrt{3}}left( 3+sqrt{5} right))

Додекаэдр

Додекаэдр составлен из двенадцати равносторонних пятиугольников.

Фигура имеет 12 граней, 20 вершин и 30 ребер (a).

Площадь поверхности додекаэдра:

( displaystyle S=3{{a}^{2}}sqrt{5left( 5+2sqrt{5} right)})

Объем додекаэдра:

( displaystyle V=frac{{{a}^{3}}}{4}left( 15+7sqrt{5} right))

Радиус описанной вокруг додекаэдра сферы:

( displaystyle R=frac{a}{4}left( 1+sqrt{5} right)sqrt{3})

Радиус вписанной в додекаэдр сферы:

( displaystyle r=frac{a}{4}sqrt{10+frac{22}{sqrt{5}}})

Решение задачи №8 на тему «Правильные многогранники»

Задача:

В кубе ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) с ребром ( displaystyle sqrt{12}) найдите ( displaystyle A{{C}_{1}}).

Решение:

( displaystyle d=asqrt{3}),

где ( displaystyle d) – диагональ куба,( displaystyle a) – сторона куба.( displaystyle A{{C}_{1}}) – это и есть диагональ куба.

Тогда ( displaystyle A{{C}_{1}}=asqrt{3}=sqrt{12}cdot sqrt{3}=sqrt{36}=6).

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж — c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Источник

История[править | править код]

Основные формулы[править | править код]

Свойства[править | править код]

Усечённый икосаэдр[править | править код]

В мире[править | править код]

Тела в виде икосаэдра[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Икосаэдр.

Икосаэдр, как правильный многогранник:

Основные формулы икосаэдра:

Свойства икосаэдра:

Общая площадь поверхности икосаэдра Калькулятор

Общая площадь поверхности икосаэдра Решение

12 Общая площадь поверхности икосаэдра Калькуляторы

10+ Площадь поверхности икосаэдра Калькуляторы

Общая площадь поверхности икосаэдра формула

Что такое икосаэдр?

Что такое Платоновые тела?

Икосаэдр

Математические характеристики икосаэдра

Популярное

Правильные многогранники

Правильные многогранники — подробнее