В данной публикации мы рассмотрим определение и разновидности тетраэдра, а также формулы для расчета площади его поверхности (одной грани и полной) и объема. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
- Определение тетраэдра
- Виды тетраэдра
- Формулы площади и объема правильного тетраэдра
Определение тетраэдра
Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.

Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.
Развертка тетраэдра на примере правильной фигуры представлена ниже:

Основные элементы и свойства тетраэдра (к нему применимы свойства правильной пирамиды) мы рассмотрели в отдельной публикации.
Виды тетраэдра
- Равногранный тетраэдр – боковые грани фигуры равны, а основанием является правильный (равносторонний) треугольник.

- Прямоугольный тетраэдр – угол между всеми тремя ребрами при одной вершине является прямым, т.е. равным 90°.

- Правильный тетраэдр – все ребра равны, а грани, соответственно, являются равносторонними треугольниками.

- Ортоцентричный тетраэдр – все высоты, проведенные из всех вершин фигуры к противолежащим граням, пересекаются в одной точке.
Формулы площади и объема правильного тетраэдра
Площадь поверхности

![]()
Объем
![]()
Площадь поверхности тетраэдра
Площадь поверхности тел
Тетраэдром является геометрическая фигура, представляющая собой простейший многогранник с четырьмя гранями. Любая грань тетраэдра является треугольником. Кроме 4-х граней у тетраэдра имеется шесть ребер и четыре вершины. В правильном тетраэдре все ребра равны. Расчет S тетраэдра необходим при решении разных проектировочных задач, т.к. он является важным конструктивным элементом в сложных строительных и других конструкциях. Площадь поверхности тетраэдра несложно вычислить с помощью онлайн калькулятора, подставив исходные данные в приведенную ниже формулу:
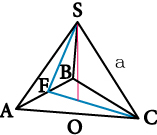
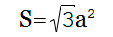
a — величина ребра тетраэдра.
Площадь тетраэдра рассчитывается как корень квадратный из произведения квадрата длины ребра на 3.
Расчет площади поверхности тетраэдра
Как найти площадь тетраэдра
Тетраэдром в стереометрии называется многогранник, который состоит из четырёх треугольных граней. Тетраэдр имеет 6 рёбер и по 4 грани и вершины. Если у тетраэдра все грани являются правильными треугольниками, то и сам тетраэдр называется правильным. Площадь полной поверхности любого многогранника, в том числе и тетраэдра можно рассчитать, зная площади его граней.

Инструкция
Чтобы найти площадь полной поверхности тетраэдра, необходимо вычислить площадь треугольника составляющего его грань.
Если треугольник равносторонний, то его площадь равна
S = √3 * 4 / a², где a – ребро тетраэдра,
тогда площадь поверхности тетраэдра находится по формуле
S = √3 * a².
В случае, если тетраэдр является прямоугольным, т.е. все плоские углы при одной из его вершин являются прямыми, то площади трёх его граней являющихся прямоугольными треугольниками можно рассчитать по формуле
S = a * b *1/2,
S = a * c *1/2,
S = b * c *1/2,
площадь третьей грани можно рассчитать по одной из общих формул для треугольников, например по формуле Герона
S = √(p * (p – d) * (p – e) * (p – f)), где p = (d + e + f)/2 – полупериметр треугольника.
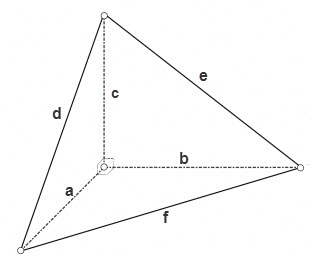
В общем случае, площадь любого тетраэдра можно рассчитать, используя формулу Герона для вычисления площадей каждой его грани.
Источники:
- площадь поверхности тетраэдра
- Найдите площадь сечения тетраэдра биссекторной плоскостью
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Площадь поверхности правильного тетраэдра
Тетраэдр — простейший многогранник, гранями которого являются четыре треугольника, треугольная пирамида. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным.

Площадь поверхности правильного тетраэдра рассчитывается по формуле:
 ,
,
где a – длина ребра.
Калькулятор площади поверхности правильного тетраэдра позволит найти площадь полной поверхности правильного тетраэдра, зная длину его ребра.
Поделиться страницей в социальных сетях:
Онлайн калькулятор площади тетраэдра может вычислить площадь боковой поверхности тетраэдра. Расчет возможен для правильного (равностороннего) тетраэдра и для прямоугольного тетраэдра.
Сделайте расчет на этом калькуляторе площади тетраэдра и получите ответ в развернутом виде а также детального пошаговое решение с выводом формул.
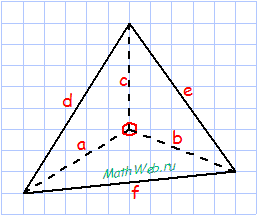
Прямоугольный тетраэдр – угол между всеми тремя ребрами при одной вершине является прямым, т.е. равным 90°
Формула площади поверхности прямоугольного тетраэдра: 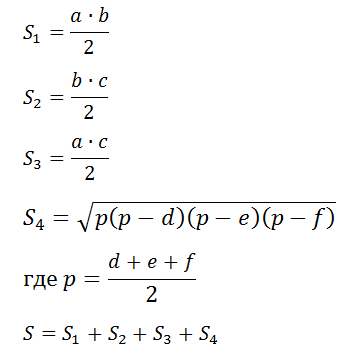
где a,b,c – стороны при угле 90°, d,e,f – стороны основания
Решение:
S1 =
=
=
= 616
S2 =
=
=
= 1144
S3 =
=
=
= 1144
p =
=
=
= 62
S4 = √p·(p-d)·(p-e)·(p-f)
= √62·(62-44)·(62-28)·(62-52)
= √62·18·34·10
= 615.987
S = S1+S2+S3+S4
= 616+1144+728+615.987
=
3103.987
Ответ: Площадь всей поверхности прямоугольного тетраэдра равна 3103.987
Тетраэдр – это разновидность пирамиды; четырехгранник, гранями которого являются треугольники.
Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Каждая грань фигуры может быть ее основанием.
