Как найти площадь всей поверхности усеченного конуса

Как найти площадь всей поверхности усеченного конуса

Как рассчитать площадь усеченного конуса

На данной странице калькулятор поможет рассчитать площадь поверхности усеченного конуса онлайн. Для расчета задайте радиусы и образующую.

Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

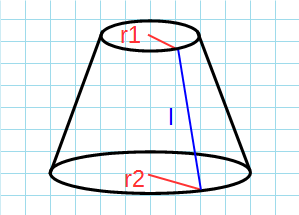
Образующая конуса – это отрезок, соединяющий вершину и границу основания.

Боковая поверхность

Площадь усеченного конуса

Формула площади боковой поверхности усеченного конуса через радиусы и образующую:

π – константа равная (3.14); r1 – радиус верхнего основания ; r2 – радиус нижнего основания; l – образующая усеченного конуса.

Полная поверхность

Площадь усеченного конуса

Формула площади полной поверхности усеченного конуса через радиусы и образующую:

π – константа равная (3.14); r1 – радиус верхнего основания ; r2 – радиус нижнего основания; l – образующая усеченного конуса.

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого усеченного кругового конуса (боковую, полную и основания), а также разберем пример решения задачи для закрепления представленного теоретического материала.

  • Формулы вычисления площади усеченного конуса

    • 1. Боковая поверхность

    • 2. Основания

    • 3. Полная площадь

  • Пример задачи

Формулы вычисления площади усеченного конуса

Усеченный конус (конический слой)

Примечание: иногда усеченный конус, также, называют коническим слоем.

1. Боковая поверхность

Чтобы найти площадь (S) боковой поверхности прямого усеченного кругового конуса, необходимо знать длину его образующей, а также радиусы двух оснований.

Sбок. = πRl + πrl = πl(R + r)

Примечание: в этой и других формулах ниже число π чаще всего округляется до 3,14.

2. Основания

Основаниями кругового усеченного конуса являются два круга, площади которых считаются таким образом:

Sосн.1 = πR 2

Sосн.2 = πr 2

Примечание: если вместо радиусов (R или r) даны соответсвующие им диаметры (d), их следует разделить на 2, чтобы получить нужные радиусы.

3. Полная площадь

Чтобы вычислить площадь полной поверхности усеченного конуса, требуется сложить площади его боковой поверхности и двух оснований.

Sполн. = πl(R + r) + πR 2 + πr 2 = π(lR + lr + R 2 + r 2)

Пример задачи

Найдите площадь поверхности усеченного конуса, если известно, что радиусы его оснований равны 6 и 11 см, а длина образующей составляет 8 см.

Решение

Все известные значения для вычисления площади нам известны, так что остается лишь подставить их в формулы, приведенные выше.

Sбок. = 3,14 ⋅ 8 см ⋅ (6 см + 11 см) = 427,04 см2

Sосн.1 = 3,14 ⋅ (11 см) 2 = 379,94 см2

Sосн.2 = 3,14 ⋅ (6 см) 2 = 113,04 см2

Sполн. = 427,04 см2 + 379,94 см2 + 113,04 см2 = 920,02 см2

Источник

Объем и площадь усеченного конуса

Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.

Радиус основания 1

см

Радиус основания 2

см

Высота

см

Размерность

Раcсчитать

Оглавление:

  • 📝 Как это работает?
  • 🤔 Частые вопросы и ответы
  • 📋 Похожие материалы
  • 📢 Поделиться и комментировать

Что считает калькулятор?

Калькулятор объема и площади усеченного конуса — это онлайн инструмент, который используется для быстрого расчета объема и площади усеченного конуса по его радиусам большего и меньшего оснований и высоте. Объем такого конуса представляет собой объем пространства, которое занимает эта фигура в трехмерном пространстве.

Калькулятор объема и площади усеченного конуса может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов и площадей таких геометрических фигур. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов и площадей, например, в архитектуре, инженерии, физике и т.д.

Где можно применить калькулятор объема и площади усеченного конуса?

Калькулятор объема и площади усеченного конуса может применяться в различных сферах, включая:

  1. Инженерия и строительство: усеченный конус может использоваться в качестве формы для создания конструкций и деталей, таких как колонны, башни, фонари, вазы и т.д. такие расчеты помогают определить необходимое количество материала для изготовления детали.
  2. Производство: усеченный конус может использоваться в качестве формы для изготовления различных изделий из металла, стекла, керамики, пластика и т.д. Расчёт его параметров помогает определить необходимое количество сырья для производства изделия.
  3. Математика: усеченный конус может быть использован для примеров и задач в математическом образовании. Расчёт объёма и площади позволяет ученикам узнать, как применять формулы для нахождения объёма и площади фигур.
  4. Машиностроение: усеченный конус может использоваться в качестве детали для различных механизмов и машин. Расчёт объёма и площади помогает определить размеры и форму детали.
  5. Архитектура и дизайн: усеченный конус может использоваться в качестве элемента декора и оформления интерьера и экстерьера зданий. Расчёт объёма и площади помогает определить оптимальный размер и форму элемента декора.

В чем преимущество усеченного конуса как геометрической фигуры?

Усеченный конус — это геометрическая фигура, у которой основаниями являются две круглые плоскости, соединенные боковой поверхностью, которая имеет форму конуса, но сечение вдоль его высоты меньше его оснований.

Преимущества этой геометрической фигуры могут включать:

  1. Усеченный конус имеет большую устойчивость, чем обычный конус, так как он имеет большую поверхность опоры на основаниях, что делает его лучшим выбором для некоторых приложений, например, при проектировании оболочек реакторов.
  2. Усеченный конус может быть более экономичным в использовании материала, чем обычный конус, так как он имеет меньшую высоту, но сохраняет ту же площадь оснований. Это может быть полезно в проектировании строительных элементов, таких как колонны или башни.
  3. Усеченный конус может иметь большую универсальность в применении, так как его форма может быть изменена путем изменения размеров его оснований и высоты. Это позволяет использовать усеченные конусы в различных областях, например, в качестве башенной опоры или формы для литья металла.
  4. Усеченный конус может иметь более эргономичную форму, что делает его удобным в использовании в некоторых приложениях, например, при проектировании мебели или автомобильных деталей.
  5. Усеченный конус может иметь более интересный внешний вид, что делает его привлекательным для использования в художественном дизайне или архитектуре.

В целом, усеченный конус является полезной геометрической фигурой, которая имеет множество преимуществ в различных областях применения.

Как вычислить объем усеченного конуса через радиусы его оснований и высоту?

Калькулятор объема и площади усеченного конуса

Для расчета объема усеченного конуса необходимо знать радиусы большего и меньшего оснований, а также высоту усеченного конуса.

Формула для расчета объема усеченного конуса:

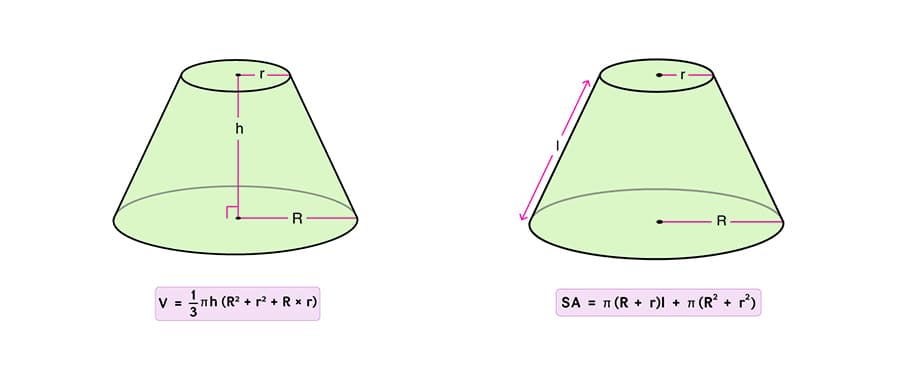
V = (1/3) * π * h * (R2 + Rr + r2)

где:

  • π – число Пи (3.14)
  • V – объем усеченного конуса
  • h – высота усеченного конуса
  • R – радиус большего основания
  • r – радиус меньшего основания

Чтобы использовать эту формулу, нужно знать значения h, R и r. Затем необходимо подставить значения в формулу и выполнить вычисления.

Пример:

Допустим, у нас есть усеченный конус с высотой 10 см, радиусом большего основания 6 см и радиусом меньшего основания 4 см. Чтобы найти объем усеченного конуса, мы можем использовать формулу:

  1. V = (1/3) * π * h * (R2 + Rr + r2)
  2. V = (1/3) * 3,14 * 10 * (6^2 + 6*4 + 4^2)
  3. V = 795,5 см3

Ответ: объем усеченного конуса равен 795,5 кубическим сантиметрам.

Как вычислить площадь усеченного конуса через радиусы его оснований и образующую?

Площадь усеченного конуса можно рассчитать с использованием следующей формулы:

S = π(r + R)ℓ + π(R2 + r2)

  • где S – площадь усеченного конуса,
  • π – математическая константа, примерно равная 3.14,
  • r1 и r2 – радиусы оснований большего и меньшего конусов соответственно,
  • и ℓ – образующая, т.е. расстояние между вершиной и основанием, вычисленная по теореме Пифагора.

Для решения задачи необходимо знать значения радиусов оснований и образующей. Если известны только высоты обоих конусов, то необходимо использовать теорему Пифагора для вычисления образующей.

После подстановки всех известных значений в формулу можно вычислить площадь усеченного конуса.

❓ Вопросы и ответы

А вот несколько ответов на часто задаваемы вопросе о шаре и его объеме.

Как пользоваться онлайн калькулятором объема и площади усеченного конуса?

Для того, чтобы использовать калькулятор объема усеченного конуса, нужно ввести значения радиусов его оснований и высоту в соответствующие поля калькулятора, затем калькулятор автоматически рассчитает объем шара. Для расчёта площади нужно проделать соответствующие действия со значениями радиусов оснований и образующей, которая вычисляется по теореме Пифагора.

Что такое усеченный конус?

Усеченный конус – это геометрическое тело, полученное из обычного конуса путем удаления верхней части тела параллельным срезом, расположенным на определенном расстоянии от вершины конуса.

Для чего нужен расчет объема усеченного конуса?

Расчет объема и площади усеченного конуса может быть полезен во многих областях, включая инженерию, архитектуру, производство и технику. Например, в производственной отрасли расчет объема и площади усеченного конуса может помочь определить количество материалов, необходимых для создания детали.

Какой материал лучше всего подходит для изготовления усеченных конусов?

Для изготовления усеченного конуса можно использовать различные материалы в зависимости от требований к конструкции. Однако, наиболее распространенными материалами для изготовления усеченных конусов являются металлы. Это может быть сталь, алюминий, медь, латунь и другие металлы. Металлические конусы обычно используются в технических приложениях, где требуется высокая прочность и устойчивость к износу.

Как вычислить образующую усеченного конуса?

Образующая конуса (l) может быть найдена с помощью теоремы Пифагора, для этого можно воспользоваться формулой: l = √((R – r)² + h²). Таким образом, чтобы вычислить образующую усеченного конуса, необходимо знать значения радиуса большего основания, радиуса меньшего основания и высоты конуса, после чего следует применить формулу, описанную выше.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

  • Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
  • Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
  • Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
  • Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
  • Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
  • Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
  • Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
  • Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
  • Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
  • Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!

Есть что добавить?

Напишите своё мнение, комментарий или предложение.

Показать комментарии

Источник

Площадь поверхности усеченного конуса

Усечённый конус или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.

Усечённый конус может быть получен вращением прямоугольной трапеции вокруг меньшей боковой стороны.

Усечённый конус

Формула площади боковой поверхности усеченного конуса: S = π l (R + r) ,

где R – радиус нижнего основания, r – радиус верхнего основания, l – образующая усеченного конуса.

Формула площади полной поверхности усеченного конуса: S = π (l R + l r + R2 + r2) ,

где R – радиус нижнего основания, r – радиус верхнего основания, l – образующая усеченного конуса.

Образующая усеченного конуса рассчитывается по формуле:

Образующая усеченного конуса ,
где R – радиус нижнего основания, r – радиус верхнего основания, h – высота усеченного конуса.

Калькулятор пощади поверхности усеченного конуса позволяет найти площадь боковой поверхности усеченного конуса и полную площадь поверхности усеченного конуса.

Поделиться страницей в социальных сетях:

Источник

Усеченный конус – это часть конуса, ограниченная между двумя параллельными основаниями перпендикулярными его оси симметрии.Основаниями конуса являются геометрические круги.
Усеченный конус
Усеченный конус может быть получен в результате вращения прямоугольной трапеции вокруг ее боковой стороны, которая является ее высотой. Границей конуса является круг радиуса R, круг радиуса r и боковая поверхность конуса. Боковую поверхность конуса описывает боковая сторона трапеции во время ее вращения.

Площадь боковой поверхности усеченного конуса через направляющую и радиусы его оснований

При нахождении площади боковую поверхность усеченного конуса целесообразней рассматривать как разность боковой поверхности конуса и боковой поверхности отсеченного конуса.
Усеченный конус
Пусть от данного конуса AMB отсекли конус A`MB`. Необходимо вычислить боковую площадь усеченного конуса AA`B`B. Известно, что радиусы его оснований AO=R, A`O`=r, образующая равна L.Обозначим MB` за x. Тогда боковая поверхность конуса A`MB` будет равна πrx. А боковая поверхность конуса AMB будет равна πR(L+x).
Тогда боковую поверхность усеченного конуса AA`B`B можно выразить через разность боковой поверхности конуса AMB и конуса A`MB`:
S_bok={pi}R(L+x)-{pi}rx={pi}(RL+Rx-rx)={pi}(RL+x(R-r))
Треугольники OMB и O`MB`– подобны по равенству углов ∠{MOB} = ∠{MO`B`} и ∠{OMB} = ∠{O`MB`}. Из подобия этих треугольников следует: R/r={L+x}/x
Воспользуемся производной пропорции. Имеем: {R-r}/r=L/x
Отсюда находим x: x={rL}/{R-r}
Подставив это выражение в формулу площади боковой поверхности, имеем: S_bok={pi}(RL+{{rL}/{R-r}} (R-r) )={pi}(RL+rL)={pi}L(R+r)
Таким образом, площадь боковой поверхности усеченного конуса равна произведению числа π на его направляющую и сумму радиусов его оснований.
Формула площади боковой поверхности усеченного конуса имеет следующий вид: S_bok={pi}L(R+r)

Иконка карандаша 24x24Пример расчета площади боковой поверхности усеченного конуса, если известны его радиус и образующая
Радиус большего основания, образующая и высота усеченного конуса равны 7, 5 и 4 см соответственно. Найдите площадь боковой поверхности конуса.
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют египетский треугольник. Это прямоугольный треугольник с соотношением сторон 3:4:5. По условию задачи образующая равна 5, а высота – 4, тогда разность радиусов основания усеченного конуса будет равна 3.
Имеем:
L=5
R=7
R=4
Формула площади боковой поверхности усеченного конуса имеет следующий вид:
S_bok={pi}L(R+r)
Подставив значения, имеем:
S_bok=5{pi}(7+4)=27{pi}

Площади боковой поверхности усеченного конуса через направляющую и средний радиус

Средний радиус усеченного конуса равен половине суммы радиусов его оснований:
R_sr={R+r}/2
R+r=2R_sr
Тогда формула площади боковой поверхности усеченного конуса может быть представлена следующим образом:
S_bok=2{pi}LR_sr
Площадь боковой поверхности усеченного конуса равна произведению длины окружности среднего сечения на его образующую.

Площади боковой поверхности усеченного конуса через радиусы его основания и угол наклона образующей к плоскости основания

Если меньшее основание ортогонально спроектировать на большее основание, то тогда проекция боковой поверхности усеченного конуса будет иметь вид кольца, площадь которого вычисляется по формуле:
S={pi}(R^2-r^2)={pi}(R-r)(R+r)
Тогда: S_bok={{pi}(R-r)(R+r)}/{cos{alpha}}

Площади боковой поверхности усеченного конуса по Архимеду

S_bok={pi}(sqrt{L(R+r)})^2
Площадь боковой поверхности усеченного конуса равна площади такого круга, радиус которого является средней пропорциональной между образующей и суммой радиусов его оснований

Полная поверхность усеченного конуса

Полная поверхность конуса – это сумма площади его боковой поверхности и площади оснований конуса:

S_poln=S_bok+S_{b.osn}+S_{m.osn}

Основаниями конуса является круги с радиусом R и r. Их площадь равна произведению числа на квадрат их радиуса:
S_{b.osn}={pi}R^2
S_{m.osn}={pi}r^2
Площадь боковой поверхности вычисляется по формуле:
S_bok={pi}L(R+r)
Тогда площадь полной поверхности усеченного конуса равна:
S_poln={pi}L(R+r)+{pi}R^2+{pi}r^2={pi}(R^2+(R+r)L+r^2)
Формула имеет следующий вид:
S_poln={pi}(R^2+(R+r)L+r^2)

Иконка карандаша 24x24Пример расчета площади полной поверхности усеченного конуса, если известны его радиус и образующая
Радиус основания усеченного конуса 1 и 7 дм, а диагонали осевого сечения взаимно перпендикулярны. Найдите площадь полную площадь усеченного конуса
Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. То есть основания трапеции равны 2 и 14 дм соответственно. Так как диагонали трапеции взаимно перпендикулярны, то высота равна полусумме ее оснований. Тогда:
h={2+14}/2=8
Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют прямоугольный треугольник.
По теореме Пифагора найдем образующую усеченного конуса:
L=sqrt{h^2+(R-r)^2}=sqrt{8^2+(7-1)^2}=sqrt{64+36}=sqrt{100}=10
Формула площади полной поверхности усеченного конуса имеет следующий вид:
S_poln={pi}(R^2+(R+r)L+r^2)
Подставив значения из условия задачи и найденные значения, имеем:
S_poln={pi}(7^2+(7+1)10+1^2)={pi}(49+80+1)=130{pi}

Источник

Добавить комментарий