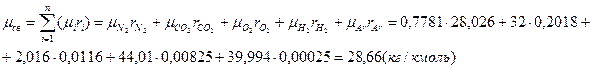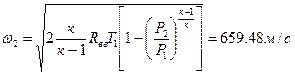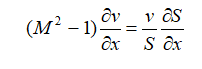3.1.1. Отношение давлений рабочего пара в выходном сечении рабочего сопла к давлению рабочего пара на входе в эжектор

3.1.2. Скорость истечения пара из рабочего сопла
Этот показатель
находят по значениям, которые приводятся
ниже
0,60 0,65
0,70 0,75 0,80 0,85 0,90 0,95
380 350 318
288 252 218 178 122
Используя
результат вычисления, полученный в п.
3.1.1, методом интерполяции находим
скорость истечения пара из рабочего
сопла w!,
которая будет равна 218 м/с. Из табл. 5
приложения, для давления Р !1
= 0,15 МПа,
определяем удельный объём пара V!
1
в выходном
сечении сопла, который равен 1,1670 м3/кг.
3.1.3. Площадь выходного сечения сопла
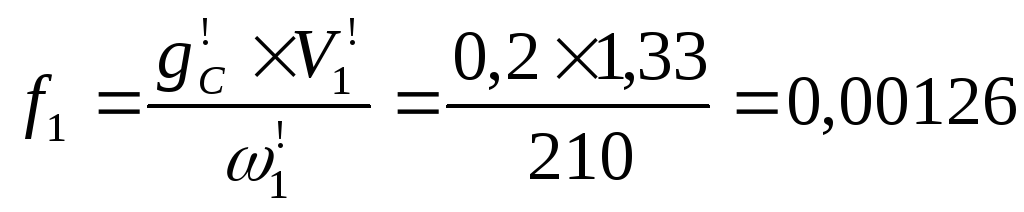
откуда диаметр
сечения 1 – 1 будет равен:
мм»40мм.
3.1.4.
Коэффициент
эжектирования
Для определения
этой величины воспользуемся рис.3,
отражающим зависимость Z
= f
(b).
Рис.3 Зависимость
Z
= f
(b)
Для значения
b
= 1,05
находим величину Z,
которая равна 3,1 и определяем коэффициент
эжектирования.
,
где Р2
= Р1!–
давление в конце камеры смешения (при
входе в диффузор – сечение 2 – 2).
3.1.5. Скорость
потока паровоздушной смеси при входе
в диффузор
м/с,
где f2–
скоростной коэффициент камеры смешения,
равный 0,975.
3.1.6. Парциальное
давление пара Рп
2 и
воздуха Рв
2 в
сечении 2 – 2

откуда Рв
2 = Р2
– Рп 2
= 0,15 – 0,121 =
0,029 МПа. По табл.5 приложения, для Рп
2 = 0,121
МПа находим t
2нас
= 104,8оС.
3.1.7. Температура
паровоздушной смеси в сечении 2 – 2
3.1.8. Удельный
объём воздуха в сечении 2 – 2
м3/кг,
где: Тсм
2 = 273 + tсм
2 = 352, 83о
К; RВ
= 29,27 кг м/кг град.
3.1.9. Объём всей
смеси в сечении 2 –2
м3/кг, тогда
3.1.10. Площадь
сечения 2 – 2
м2,
где: G
= gc!
´
(1+ U)
= 0,2 ´
(1 + 1,07) = 0,414 кг/с; h-
коэффициент, учитывающий неравномерное
распределение скоростей. Принимается
в пределах от 1,3 до 1,5.
3.1.11. Диаметр
сечения 2-2
88,1 мм»88мм.
3.2. Определение
площади сечений горловины и диффузора
(сжатие в диффузоре)
3.2.1. Показатель
адиабаты
.
Откуда К =
1,155
где К – показатель
адиабаты сжимаемой паровоздушной смеси.
КП
– показатель
адиабаты для пара, равный 1,135; КВ
– показатель
адиабаты для воздуха, равный 1,4.
3.2.2. Показатель
политропы
n
= k
+ 0,183 = 1,155
+ 0,183 = 1,338.
3.2.3. Скорость
звука в сечении 2-2
407,23м/с.
3.2.4. Число Маха
.
3.2.5. Степень
повышения давления до горловины диффузора

откуда Р3
= b!
´
Р2
= 0,548
´
0,15
= 0,0822
МПа.
3.2.6. Удельный
объём паровоздушной смеси в сечении
3-3 диффузора

3.2.7. Скорость
звука в сечении 3-3
376,67
м/с.
3.2.8. Скорость
паровоздушной смеси в сечении 3-3
м/с.
3.2.9. Площадь
сечения горловины
м2.
3.2.10. Диаметр
горловины
мм»58мм.
3.2.11. Давление
паровоздушной смеси в сечении 4-4(в конце
диффузора)
МПа.
3.2.12. Удельный
объём паровоздушной смеси в сечении
4-4(в конце диффузора)
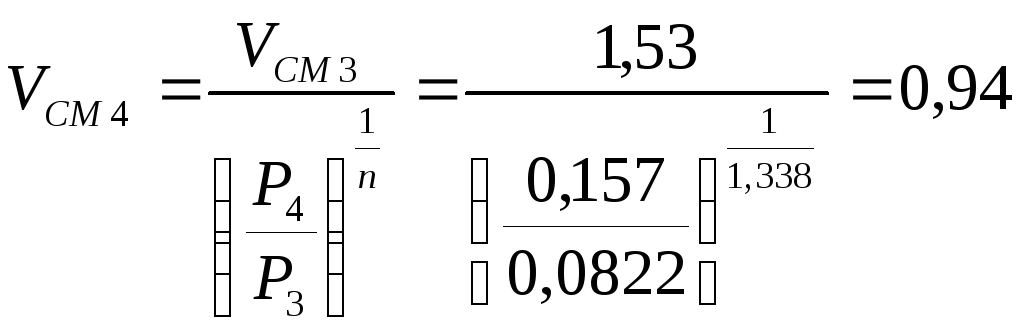
3.2.13. Площадь
выходного сечения диффузора
Для определения
этой величины примем скорость истечения
паровоздушной смеси в сечении 4 – 4,
равной 50 м/с.
м2.
3.2.14. Диаметр
выходного сопла диффузора
мм»100 мм.
3.3. Определение
осевых размеров эжектора
3.3.1. Длина
сужающейся части сопла
Принимаем диаметр
цилиндрической части входного сопла
d0
= 50 мм и угол конусности A1
в пределах от 6 до 8о.

3.3.2. Длина
сужающейся части диффузора

где А2
= А1.
3.3.3. Длина
горловины диффузора
мм
3.3.4. Длина
расходящейся части диффузора

где А3
– угол конусности расходящейся части
диффузора, равный 7 – 10о.
-
Конструктивная
часть
Рис.1.
Кассетно-формовочная установка
Кассетно-формовочная
установка (рис. 1) состоит из кассеты 1
и машины 11 для распалубки и сборки
кассет. Установка предназначена для
изготовления панелей внутренних стен
и перекрытий, применяемых в крупнопанельном
домостроении. Машина для распалубки и
сборки кассет состоит из рамы,
гидроцилиндра, системы запорных рычагов
с амортизаторами, регулировочных винтов,
гидроаппаратуры и электрооборудования.
Рама образована двумя (передней 12 и
задней 6) стойками, соединенными между
собой опорными балками 7, на которые
установлены своими катками стенки
кассетной формы. К передней стойке рамы
прикреплены кронштейны рычажной системы
гидропривода, гидроцилиндр 11 и конечные
выключатели.
При,
помощи тяг рычажная система соединена
с запорными рычагами. На задней стойке
рамы установлены регулировочные винты
для получения требуемой толщины и
правильного положения пакета при сборке.
Амортизаторы 4, шарнирно соединенные с
рычажной системой и регулировочными
винтами 5, приварены к наружным поверхностям
стационарной 3 и съемной 13 стенок
кассетной формы. Гидроцилиндр и система
рычагов 10 перемещают стенки на 850 мм.
Пульт управления и электрошкаф монтируют
рядом с кассетно-формовочной установкой
на обслуживающей площадке.
Кассетная
форма представляет собой пакет
металлических стенок и тепловых отсеков,
между которыми бортовой оснасткой
образованы формовочные отсеки. По
конструктивным признакам и назначению
стенки можно разделить на тепловые,
промежуточные и крайние (стационарные
и съемные). В собранной форме тепловые
стенки 1 и промежуточные стенки 2
чередуются. Тепловая стенка, к которой
подводится пар для подогрева бетонной
смеси при тепловой обработке, выполнена
из двух металлических листов толщиной
24 мм и швеллеров, прикрепленных по
контуру стенки. Тепловая стенка должна
быть герметичной. Крайняя тепловая
стенка 1 с внешней стороны снабжена
теплоизоляционным щитом. Промежуточные
стенки кассетной формы выполнены из
листа толщиной 24 мм.
Все
стенки формы, кроме крайней-съемной,
снабжены бортовой оснасткой в соответствии
с толщиной формуемых изделий.
На
консольных участках промежуточных
стенок с обеих сторон на’ кронштейнах
смонтированы электромеханические
вибраторы ИВ-I04, предназначенные для
вибрации стенок в процессе заполнения
кассетной формы бетонной смесью.
Вибраторы 14 установлены так, что ось их
параллельна плоскости стенок. Колебания
промежуточной стенки следует
рассматривать как вынужденные колебания
упругого бруса, размещенного на двух
шарнирно неподвижных опорах и имеющего
две консоли, к которым приложена
вынуждающая сила. Частота колебаний
стенки 1400 кол./ мин соответствует частоте
колебаний вибратора. Наиболее эффективная
вибрация наблюдается при установке
вибратора на консоли длиной
65
… 68 см. Амплитуда колебаний промежуточных
стенок 0,08 .. 0,30 мм.
В
верхней части кассетная форма снабжена
четырьмя защитными козырьками,
предотвращающими просыпание бетонной
смеси. Пар по рукавам подводится к
тепловым стенкам-отсекам от распределительных
гребенок. В тепловых отсеках установлены
перфорированные трубки, через которые
пар попадает в отсек. Для стока конденсатора
в нижней части теплового отсека
предусмотрен патрубок с краном. На
стенках установлены замки 8 для их
сцепления. Штанга замка в верхней части
соединена с эксцентриком, при повороте
которого она поднимается или опускается
и при этом соединяет или разъединяет
отсеки формы.
К
верхнему торцу каждой стенки кассеты
справа и слева приварены
кронштейны
для крепления ролико – опор 9, предназначенных
для перемещения стенок кассеты по
направляющим рамы машины при разборке
и сборке кассеты.
Изделия
изготовляют следующим образом. Отсек,
образованный крайней стационарной
стенкой и разделительным листом,
подготавливают к формованию. После
чистки поверхностей и удаления остатков
бетона устанавливают и закрепляют
закладные детали и проемообразователей
и поверхности листов смазывают.
Арматурный
каркас подается в отсек и фиксируется
в требуемом положении. Гидроцилиндром
весь пакет стенок перемешается в сторону
стационарной стенки до упора. С помощью
замков к стационарной стенке крепят
разделительную стенку, освобождая ее
от остального пакета, который тем же
гидроцилиндром отводится назад, раскрывая
следующий отсек для чистки, смазывания
и установки арматурного каркаса. Затем
гидроцилиндром подводится пакет,
оставляется следующая стенка, закрывающая
второй, подготовленный к бетонированию
отсек, а пакет отодвигается назад,
раскрывая третий отсек, и т. д. до
последнего отсека. Последней подводится
съемная стенка. Запорные рычаги сжимают
весь пакет.
Конструкция
распалубочной машины предусматривает
два автоматических механизма запирания
пакета, предохраняющих кассету от
самопроизвольного раскрытия в процессах
формования и термообработки изделий.
Первый
механизм, осуществляющий первичное
запирание пакета кассеты, работает
следующим образом. Благодаря смещению
(эксцентриситету) складных рычагов от
центрального шарнира вниз относительно
осей их крайних шарниров горизонтальная
сила от распора па кета кассеты удерживает
рычаги от самопроизвольного складывания
(при отключенном приводе насосной
станции за счет наличия вышеуказанного
эксцентриситета между осями запорных
рычагов).
Второй
механизм осуществляет вторичное
запирание па кета кассеты.
Форма
подготовлена к бетонированию. После
подачи бетонная смесь уплотняется.
Далее в тепловые отсеки формы подается
пар и в соответствии с принятым режимом
производится тепловая обработка.
Разбирается форма аналогично сборке,
но в обратном порядке. Изделия вынимают
из отсеков краном.
17
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для предотвращения
отрыва потока от стенок сопла в сверхзвуковой его части конусность расширяющегося
участка рекомендуется выбирать в пределах от 8 до 12˚. Площадь верхнего сечения
сопла выбирается из условия достижения в этом сечении давления газа, равного
давлению окружающей среды. При соблюдении этого условия сопло называется
расчетным. Скорость в выходном сечении определяется формулой (5), а площадь при
сохранении постоянного расхода, равного критическому, равна:
(15)
Важной
характеристикой потоков сжимаемого газа является число Маха , равное отношению скорости
потока к скорости звука.
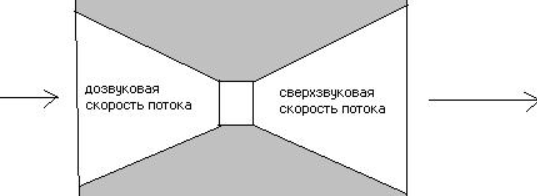
При М<1 поток
называется дозвуковым, при М>1- сверхзвуковым.
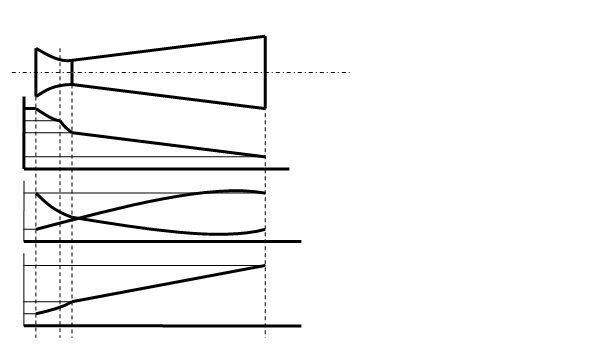
Рис2.
Истечение газа
а-комбинированное сопло; б- уменьшение давления газа по длине сопла;
в- изменение скорости
потока ω и скорости а по длине сопла; г- изменение удельного объема по длине
сопла.
На рисунке 2,а
изображена схема комбинированного сопла для получения сверхзвуковой скорости;
процесс расширения газа должен проходить без отрыва от стенок; опытами
установлено, что это условие выполняется, если угол конусности расширяющейся
части сопла β=10…12˚
На рисунке 2,б,в
изображено распределение параметров p,v, a скорости потока ω и скорости звука а по длине
сопла в процессе адиабатного расширения, давление в конце расширения равно
давлению окружающей среды. Для адиабатного процесса расширение распределения
скорости по длине сопла можно построить по формуле ,
например, для точки х (рис. 2а) скорость равна .
Располагаемая
работа lx численно равна заштрихованной площади на рис. 2б.
Площадь поперечного
сечения сопла для заданного расхода М для сечения х равна:
(2)
Расчет сопла Лаваля.
Дано:
рабочее
тело-воздух (рассматривать, как идеальный газ);
массовый секундный расход воздуха m=1,8 кг/с;
температура на входе в Сапло t1=61 0C;
давление на входе в сапло P1=3,4 МПа;
относительная влажность входящего воздуха φ=56 %;
давление
окрестностей среды P2=0,1 МПа;
коэффициент
скорости φ=0,95;
угол
раствора сопла α=11;
Требуется:
1.
Определить
термодинамические параметры и скорость воздуха на входе в минимальное сечение и
на выходе из сопла.
2.
Рассчитать геометрические
размеры сопла.
3.
Изобразить в T-S
координатах процесс адиабатного расширения воздуха при истечении из сопла.
4.
Показать качественную
картину изменения давления, скорости и объема воздуха по длине сопла.
Определяем удельную
газовую постоянную влажного воздуха.
Молекулярная масса
сухого воздуха:
Молекулярная масса
водяного пара μпара=2∙1,008+16=18,016(кг/кмоль)
Из таблицы ‘
Насыщенный водяной пар’ по t1 находим Pн.
Pн=0,020938
МПа
0,56∙0,020938=0,011725 МПа
Тогда объемная доля
водяного пара во влажном воздухе:
0,00345
Доля сухого воздуха
во влажном rсв=1-rвп=0.9965
Молекулярная масса
влажного воздуха:
28,66∙0,9965+18,016∙0,00345=28.62
кг/кмоль
290.49Дж/(кг к)
Определяем
теоретическую скорость истечения воздуха из сопла w2:
Действительная
скорость истечения:
=659,48∙0,95=626,51м/с, где
ψ- скоростной коэффициент;
Для того чтобы
определить площадь выходного сечения сопла, необходимо определить температуру
газа на выходе из сопла при адиабатическом истечении:
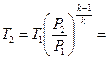
Действительная
температура воздуха на выходе из сопла:
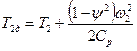
1016,715Дж/(кг К)
Определяем удельный
объем газа в выходном сечении:
0,4096 м3/кг
Определяем площадь
поперечного выходного сечения сопла:
1,18∙10-3 м2
0,039 м
= 39
мм
При достижении Р2
критического давления Р2=Ркр; Ркр=Р1βкр.
Для воздуха βкр=0,528.
Ркр в
минимальной части соплаРкр=Р1βкр=1,795
МПа
Критическая
скорость истечения в минимальном сечении сопла:
336,44м/с
Действительная
скорость
=319,62 К
Критическая
температура:
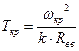
Действительная
критическая температура:
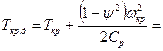
Действительный
удельный расход:
0,046 м2/кг
Площадь в минимальном
сечении сопла:
0,000259
м2
Диаметр минимального
сечения сопла:
0,018 м
dmin =18мм
Диаметр на входе в
сопло принимается d1=1,1…1,2∙dmin
d1=1,1∙dmin=19,8 мм
l1= d1=19,8 мм
Длина расширяющейся
части сопла:
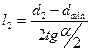
Для построения
графика адиабатного истечения воздуха из сопла определяем изменение энтропии с
учётом трения:
ΔS=S2д– S2==162,95 Дж/(кг К)
Список литературы:
1.
В.И.Кушнарев, В.И.Лебедев,
В.А.Павленко, ‘Техническая термодинамика и теплопередача’ М.: ‘Высшая школа’,
1986
Расчёт сопел современных ракетных двигателей
Время на прочтение
10 мин
Количество просмотров 52K
Введение
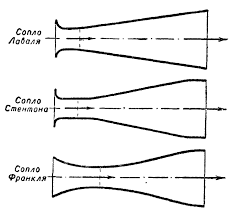
Сопло ракетного двигателя- техническое приспособление, которое служит для ускорения газового потока, проходящего по нему до скоростей, превышающих скорость звука. Основные виды профилей сопел приведены на рисунке:
По причине высокой эффективности ускорения газового потока, нашли практическое применение сопла Лаваля. Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами:
В ракетном двигателе сопло Лаваля впервые было использовано генералом М. М. Поморцевым в 1915 году. В ноябре 1915 года в Аэродинамический институт обратился генерал М. М. Поморцев с проектом боевой пневматической ракеты.
Ракета Поморцева приводилась в движение сжатым воздухом, что существенно ограничивало ее дальность, но зато делало ее бесшумной. Ракета предназначалась для стрельбы из окопов по вражеским позициям. Боеголовка оснащалась тротилом.
В ракете Поморцева было применено два интересных конструктивных решения: в двигателе имелось сопло Лаваля, а с корпусом был связан кольцевой стабилизатор. Подобные конструкции используются и в настоящее время, но уже с твёрдотопливным двигателем и системой автоматического наведения:
Однако проблемы остались старые, но уже в современном исполнении: ограниченная дальность до 3 км., наведение и удержание цели в условиях хорошей видимости, что для настоящего боя не реально, не защищённость от электромагнитных заградительных помех и, наконец, но не в последнюю очередь, высокая стоимость.
Теоретические основы
Эффективные сопла современных ракетных двигателей профилируются на основании специальных газодинамических расчётов. Основное уравнение, связывающее градиент площади сечения, градиент скорости и число Маха, следующее:
где: S – площадь сечения сопла; v – скорость газа; M – число Маха (отношение скорости газа в какой-либо точке потока к скорости звука в этой же точке).
Анализируя это соотношение, получаем, что в сопле Лаваля могут осуществляться следующие режимы течения:
1) M <1 – поток на входе дозвуковой: [1]
а) 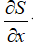
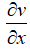
б) 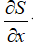
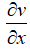
2) M>1 – поток на входе сверхзвуковой:
а) 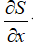
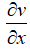
б) 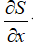
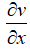
3) 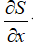
Тогда возможно либо М = 1 (поток переходит через скорость звука), либо 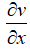
Какой из режимов реализуется на практике, зависит от перепада давлений между входом в сопло и окружающей средой.
Если давление, достигаемое в критическом сечении, превышает наружное давление, то поток на выходе из сопла будет сверхзвуковым. В противном случае он остается дозвуковым. [2]
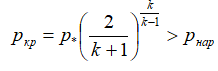
где: p* – давление торможения (давление в камере); pкр – давление в критическом сечении сопла; pнар – давление в окружающей среде; k – показатель адиабаты.
Если известны параметры в камере сгорания, то параметры в любом сечении сопла можно узнать по следующим соотношениям:
давление:
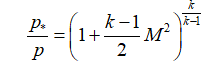
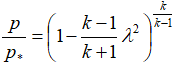
температуру:
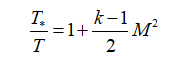
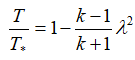
плотность:
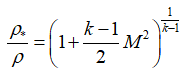
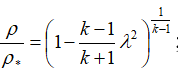
скорость:
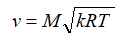
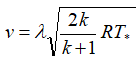
В этих формулах – λ – приведенная скорость, отношение скорости газа в данном сечении сопла к скорости звука в критическом сечении, R – удельная газовая постоянная. Индексом «*» обозначены параметры торможения (в данном случае – параметры в камере сгорания).
Постановка задачи
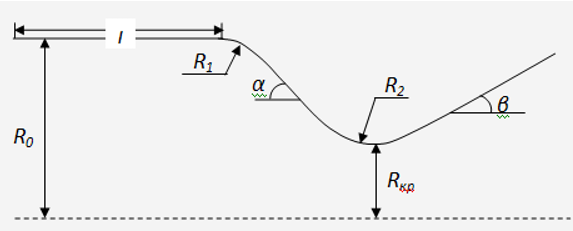
1. Рассчитать параметры течения потока газов в сопле Лаваля: для этого профиль сопла Лаваля разбивается на 150 контрольных точек – 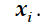
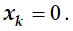
2. Расчёты выполнить средствами высокоуровневого свободно распространяемого языка программирования Python по следующей расчётной схеме и исходным данным:
Рисунок 1-Профиль сопла Лаваля
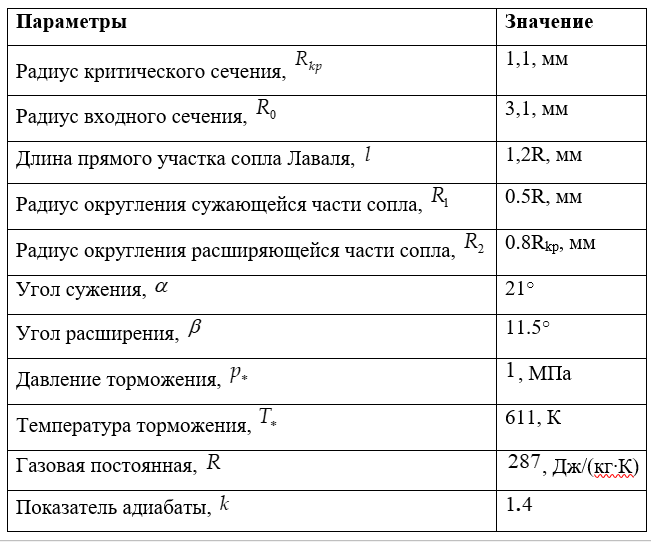
Таблица 1-Исходные данные
Приведенные исходные данные носят демонстрационный характер.
Расчёт сопла Лаваля средствами Python
Листинг для построения профиля и площади проходного сечения сопла Лаваля
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr# Радиус округления сужающейся части сопла
r2=0.8*rkr# Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):
if x0<=x<=xa:
return ya*1e-4
if xa<=x<=xc:
return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
if xc<=x<=xd:
return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
if xd<=x<=xf:
return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
if xf<=x:
return (yf+tan(radians(beta))*(x-xf))*1e-4
y=[R(x+xe) for x in np.arange(-5,5,0.01)]
x=np.arange(-5,5,0.01)
plt.figure()
plt.title('Профиль сопла ')
plt.axis([-5.0, 5.0, 0.0, 3.0*10**-4])
plt.plot(x,y,'r')
plt.grid(True)
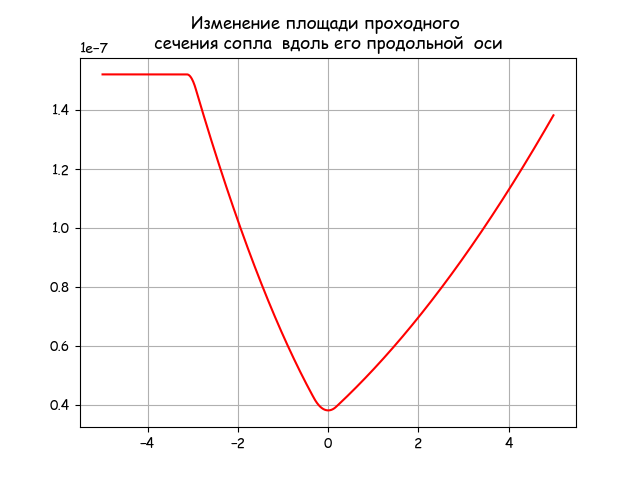
plt.figure()
plt.title('Изменение площади проходного n сечения сопла вдоль его продольной оси ')
yy=[pi*R(x+xe)**2 for x in np.arange(-5,5,0.01)]
plt.plot(x,yy,'r')
plt.grid(True)
plt.show()
Для продолжения решения задачи на Python, нужно связать λ – приведенную скорость газа с координатой x вдоль продольной оси. Для этого я воспользовался функцией fsolve из библиотеки SciPy со следующей инструкцией:
fsolve(<функция>,<стартовая точка>,xtol=1.5 · 10^8)
Привожу фрагмент программы для управления решателем с одной стартовой точкой:
def lamda(z):
m=round(Q(z),2)
if z>= 0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
return x[0]
if z<0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
return x[0]Это единственно возможное на Python решение сложного алгебраического уравнения со степенной функцией от показателя адиабаты k. Например, даже для упрощённого уравнения с использованием библиотеки SymPy, получим недопустимое время расчёта только одной точки:
from sympy import *
import time
x = symbols('x',real=True)
start = time.time()
start = time.time()
d=solve( 1.5774409656148784068*x *(1.0-0.16666666666666666667*x**2)**2.5-0.25,x)
stop = time.time()
print ("Время работы решателя:",round(stop-start,3))
print(round(d[0],3))
print(round(d[1],3))
Время работы решателя: 195.675
0.16
1.95
Листинг для вычисления газодинамической функции относительной скорости
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
from scipy.optimize import *
import time
start = time.time()
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr#Радиус округления сужающейся части сопла
r2=0.8*rkr#Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):
if x0<=x<=xa:
return ya*1e-4
if xa<=x<=xc:
return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
if xc<=x<=xd:
return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
if xd<=x<=xf:
return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
if xf<=x:
return (yf+tan(radians(beta))*(x-xf))*1e-4
def S(x):
return pi*R(x+xe)**2
xg=2*xe
n=150
RG=287 #Газовая постоянная
Tt=611 #Температура торможения
k=1.4
def tau(x):
return 1-(1/6)*x**2
def eps(x):
return (1-(1/6)*x**2)**2.5
def pip(x):
return 1-(1/6)*x**2
def Q(z):
return S(0)/S(z)
x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)]
def lamda(z):
m=round(Q(z),2)
if z>= 0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
return x[0]
if z<0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
return x[0]
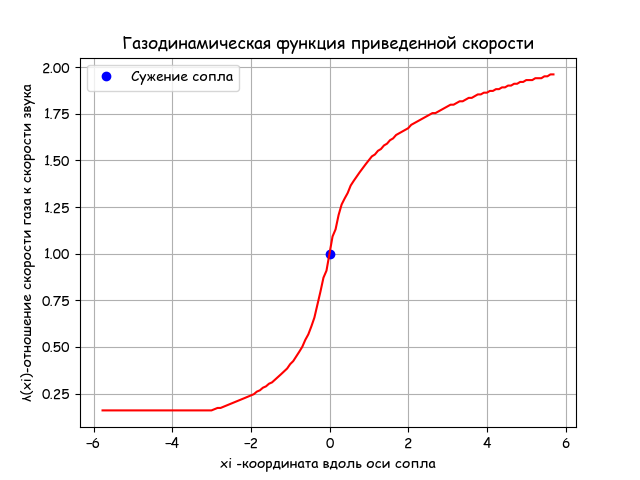
plt.title('Газодинамическая функция приведенной скорости')
y=[lamda(z) for z in x]
stop = time.time()
print ("Время работы программы:",round(stop-start,3))
plt.ylabel('λ(xi)-отношение скорости газа к скорости звука' )
plt.plot(0, 1, color='b', linestyle=' ', marker='o', label='Сужение сопла')
plt.xlabel('xi -координата вдоль оси сопла')
plt.plot(x,y,'r')
plt.legend(loc='best')
plt.grid(True)
plt.show()
Время работы программы: 0.222
Вывод:
Полученная эпюра распределения скоростей газового потока полностью соответствует изложенной выше теории. При этом, по предложенному алгоритму и библиотеке, время расчёта в 150 точках в 1000 раз меньше, чем для одной точки с использованием solve sympy.
Листинг для вычисления газодинамической функции температуры
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
from scipy.optimize import *
import time
start = time.time()
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr#Радиус округления сужающейся части сопла
r2=0.8*rkr#Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):
if x0<=x<=xa:
return ya*1e-4
if xa<=x<=xc:
return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
if xc<=x<=xd:
return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
if xd<=x<=xf:
return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
if xf<=x:
return (yf+tan(radians(beta))*(x-xf))*1e-4
def S(x):
return pi*R(x+xe)**2
xg=2*xe
n=150
RG=287 #Газовая постоянная
Tt=611 #Температура торможения
k=1.4
def tau(x):
return 1-(1/6)*x**2
def eps(x):
return (1-(1/6)*x**2)**2.5
def pip(x):
return 1-(1/6)*x**2
def Q(z):
return S(0)/S(z)
x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)]
def lamda(z):
m=round(Q(z),2)
if z>= 0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
return x[0]
if z<0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
return x[0]
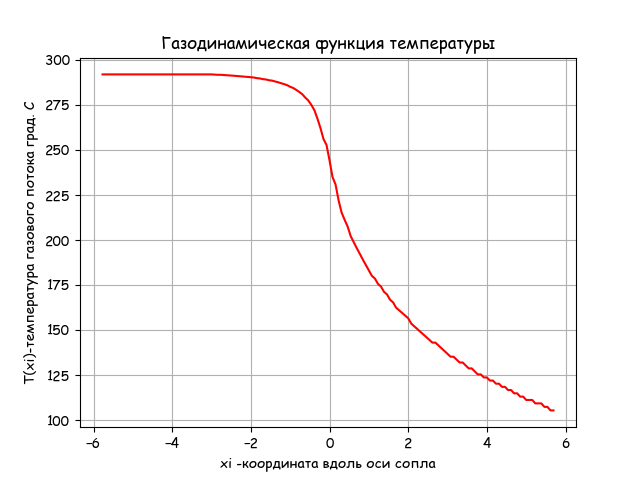
plt.title('Газодинамическая функция температуры')
t0=293
y=[ t0*tau(lamda(z)) for z in x]
stop = time.time()
print (" Время работы программы:",round(stop-start,3))
plt.ylabel('T(xi)-температура газового потока град. С' )
plt.xlabel('xi -координата вдоль оси сопла')
plt.plot(x,y,'r')
plt.grid(True)
plt.show()
Время работы программы: 0.203
Вывод
Температура на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое –0.203.
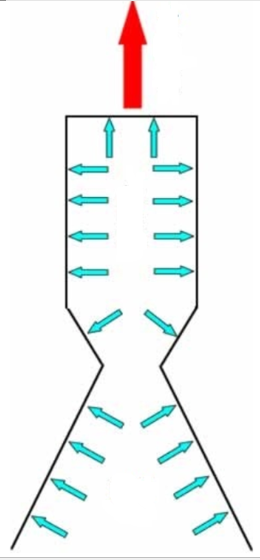
Испытательная установка:
Листинг для вычисления газодинамической функции давления
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
from scipy.optimize import *
import time
start = time.time()
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr#Радиус округления сужающейся части сопла
r2=0.8*rkr#Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):
if x0<=x<=xa:
return ya*1e-4
if xa<=x<=xc:
return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
if xc<=x<=xd:
return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
if xd<=x<=xf:
return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
if xf<=x:
return (yf+tan(radians(beta))*(x-xf))*1e-4
def S(x):
return pi*R(x+xe)**2
xg=2*xe
n=150
RG=287 #Газовая постоянная
Tt=611 #Температура торможения
k=1.4
def tau(x):
return 1-(1/6)*x**2
def eps(x):
return (1-(1/6)*x**2)**2.5
def pip(x):
return 1-(1/6)*x**2
def Q(z):
return S(0)/S(z)
x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)]
def lamda(z):
m=round(Q(z),2)
if z>= 0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
return x[0]
if z<0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
return x[0]
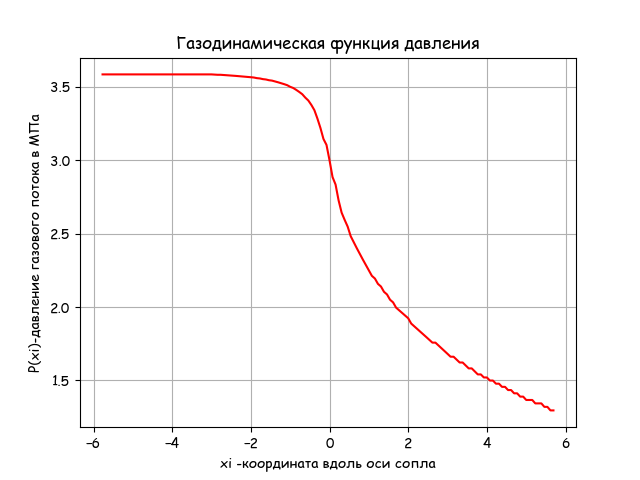
plt.title('Газодинамическая функция давления')
p0=3.6
y=[ 3.6*pip(lamda(z)) for z in x]
stop = time.time()
print ("Время работы программы:",round(stop-start,3))
plt.ylabel('P(xi)-давление газового потока в МПа' )
plt.xlabel('xi -координата вдоль оси сопла')
plt.plot(x,y,'r')
plt.grid(True)
plt.show()
Время работы программы: 0.203
Вывод
Давление на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое -0.203.
Возникновение силы тяги от действия давления газа схематично показано на рисунке:
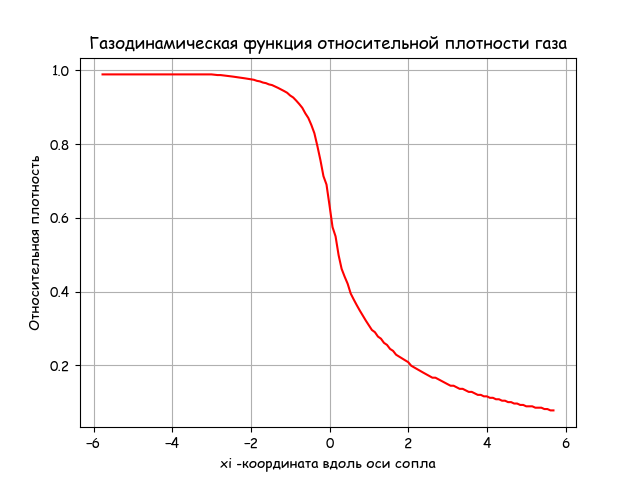
Листинг для вычисления газодинамической функции относительной плотности газа
#!/usr/bin/env python
#coding=utf8
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'fantasy'
mpl.rcParams['font.fantasy'] = 'Comic Sans MS, Arial'
import numpy as np
from math import *
from scipy.optimize import *
import time
start = time.time()
alfa=21.0#Угол сужения
beta=11.5#Угол расширения
rkr=1.1#Радиус критического сечения
R0=2*rkr
r1=0.5*rkr#Радиус округления сужающейся части сопла
r2=0.8*rkr#Радиус округления расширяющейся части сопла
ye=rkr+r2
L=1.2*R0#Длина прямого участка сопла Лаваля
x0=0
y0=R0
xa=L
ya=y0
xc1=xa
yc1=ya-r1
xc=xa+r1*cos(radians(90-alfa))
yc=yc1+r1*sin(radians(90-alfa))
yd=ye-r2*sin(radians(90-alfa))
xd=xc+(yc-yd)/tan(radians(alfa))
xc2=xd+r2*sin(radians(alfa))
xe=xc2
xf=xe+r2*cos(radians(90-beta))
yf=ye-r2*sin(radians(90-beta))
def R(x):
if x0<=x<=xa:
return ya*1e-4
if xa<=x<=xc:
return (yc1+sqrt(r1**2-(x-xc1)**2))*1e-4
if xc<=x<=xd:
return (-tan(radians(alfa))*(x-xc)+yc)*1e-4
if xd<=x<=xf:
return (ye-sqrt(r2**2-(x-xe)**2))*1e-4
if xf<=x:
return (yf+tan(radians(beta))*(x-xf))*1e-4
def S(x):
return pi*R(x+xe)**2
xg=2*xe
n=150
RG=287 #Газовая постоянная
Tt=611 #Температура торможения
k=1.4
def tau(x):
return 1-(1/6)*x**2
def eps(x):
return (1-(1/6)*x**2)**2.5
def pip(x):
return 1-(1/6)*x**2
def Q(z):
return S(0)/S(z)
x=[x0-xe+(i/n)*(xg-x0) for i in np.arange(0,n,1)]
def lamda(z):
m=round(Q(z),2)
if z>= 0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,1.5)
return x[0]
if z<0:
x=fsolve(lambda x:x*( (1-(1/6)*x**2)**2.5)/((1-(1/6))**2.5)-m,0.5)
return x[0]
plt.title('Газодинамическая функция относительной плотности газа')
y=[ eps(lamda(z)) for z in x]
stop = time.time()
print ("Время работы программы:",round(stop-start,3))
plt.ylabel('Относительная плотность' )
plt.xlabel('xi -координата вдоль оси сопла')
plt.plot(x,y,'r')
plt.grid(True)
plt.show()
Время работы программы: 0.203
Вывод
Плотность газа на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое.
Выводы
- Разработан метод решения средствами Python вещественных корней нелинейных степенных уравнений с дробными показателями степени используемых для описания газодинамических процессов. Метод основан на применении решателя fsolve из модуля scipy. optimize.
- С помощью разработанного метода, решена демонстрационная задача расчёта сопла современных ракетных двигателей с определением следующих газодинамических функций: скорости; температуры; давления; плотности реактивных газов.
Ссылки
1. А. А. Дорофеев Основы теории тепловых ракетных двигателей (Общая теория ракетных двигателей) МГТУ им. Н. Э. Баумана Москва 1999 г.
2. Ландау Л. Д., Лифшиц Е. М. Глава X. Одномерное движение сжимаемого газа. § 97. Истечение газа через сопло // Теоретическая физика. — Т. 6. Гидродинамика.
Площадь – выходное сечение – сопло
Cтраница 1
Площадь выходного сечения сопла подсчитывается по уравнению ( 8 – 30), которое, разумеется, справедливо для течения любых сред.
[1]
Поскольку площадь выходного сечения сопла нельзя сделать бесконечно большой, то такой расчетный режим не может быть реализован.
[3]
Для этого площадь выходного сечения сопла горелки изменяется путем перемещения специального конусо-ебразного сердечника-дросселя.
[4]
Относительная погрешность измерения площади выходного сечения сопла / 2 определяется точностью приборов, используемых для измерения диаметра сопла.
[5]
Давление рс считается одинаковым на всей площади выходного сечения сопла и измеряется в избыточных атмосферах.
[6]
Вторая составляющая создается давлением рабочей жидкости на площадь выходного сечения сопла. Наконец, третья составляющая обусловлена давлением рабочей жидкости в зазоре между торцом сопла и заслонкой.
[7]
Известен принцип регулирования производительности эжектора путем изменения площади выходного сечения сопла с помощью регулирующей иглы. Однако этот принцип имеет ряд существенных недостатков. При вдвигании иглы в сопло изменяется вся аэродинамическая картина работы эжектора. Для поддержания постоянного коэффициента эжекции необходима весьма сложная система соединения привода регулирующей иглы с регулирующей заслонкой в воздушном патрубке эжектора. Эжектор неустойчиво работает на малых расходах.
[8]
Одно из направлений таких разработок охватывает способы регулирования площади выходного сечения сопла.
[10]
Из этой формулы следует, что секундный расход газа является функцией площади выходного сечения сопла, начального состояния газа на входе в сопло и давления окружающей среды, в которую происходит истечение.
[11]
РН – давление в среде, куда происходит истечение, Si – площадь выходного сечения сопла.
[12]
Найти давление торможения в ресивере, откуда происходит истечение, массовый расход и площадь выходного сечения сопла, считая течение изэнтропическим и режим работы сопла Лаваля расчетным.
[13]
Скорость истечения и удельный расход газа при до-критическом перепаде давлений не зависят от площади выходного сечения сопла, а полный расход газа прямо пропорционален площади выходного сечения. Так, например, сопла, изображенные на рис. 9.5, имеющие одинаковые размеры выходного сечения и работающие при одинаковых давлениях р и рп дают одинаковые расходы газа.
[15]
Страницы:
1
2
3