Факт 1.
(bullet) Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними.
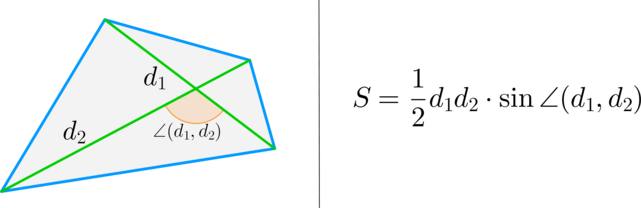
Факт 2.
(bullet) Формула Брахмагупты:
если около четырехугольника можно описать окружность, то его площадь равна [{large{S=sqrt{(p-a)(p-b)(p-c)(p-d)}}}]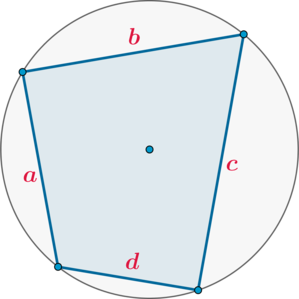 
где (a,b,c,d) – его стороны, (p) – полупериметр.
Факт 3.
(bullet) Если в четырехугольник можно вписать окружность, то его площадь равна [{large{S=pcdot r}}]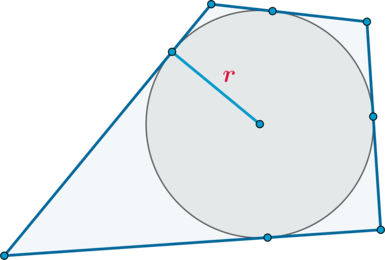 
где (p) – полупериметр, (r) – радиус вписанной окружности.
Факт 4.
(bullet) Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна [{large{S=sqrt{abcd}}}]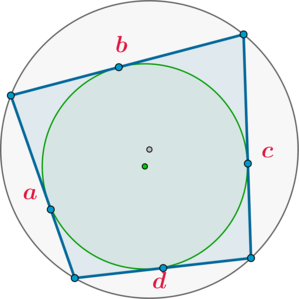 
где (a,b,c,d) – его стороны.
Выпуклый четырехугольник – это геометрическая фигура, полученная путем соединения на плоскости четырех точек, которые не должны лежать на одной прямой. При этом образованные таким образом стороны не должны пересекаться.
-
Формула вычисления площади
- По диагоналям и углу между ними
-
По четырем сторонам (формула Брахмагупты)
- По радиусу вписанной окружности и сторонам
- Пример задачи
Формула вычисления площади
По диагоналям и углу между ними
Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними.
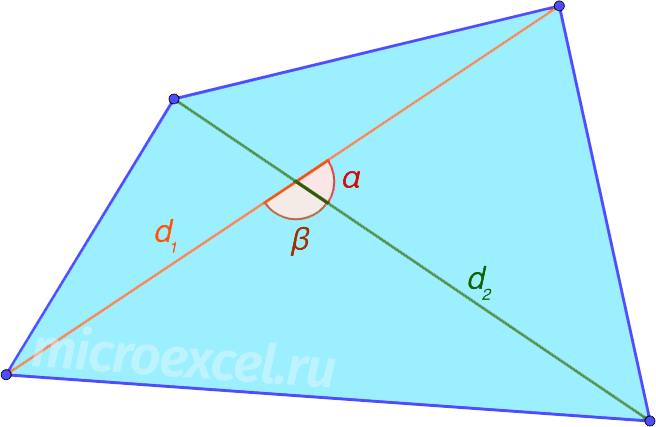
По четырем сторонам (формула Брахмагупты)
Чтобы воспользоваться формулой, необходимо знать длины всех сторон фигуры. Также вокруг четырехугольника должна быть возможность описать окружность.
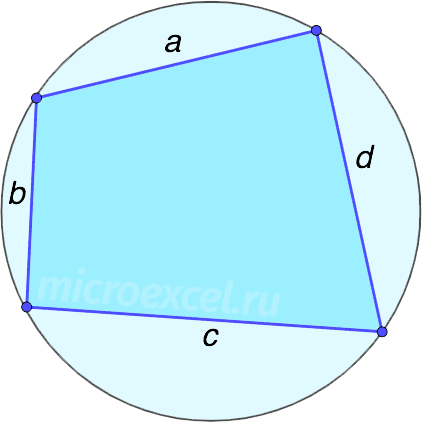
p – полупериметр, вычисляется следующим образом:
По радиусу вписанной окружности и сторонам
Если в четырехугольник можно вписать окружность, вычислить его площадь можно, воспользовавшись формулой:
S = p ⋅ r
r – радиус окружности.
Пример задачи
Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.
Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см2.
Площади четырехугольников
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
,
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник |  |
S = ab | |
 |
|||
 |
|||
| Параллелограмм |  |
||
 |
|||
 |
|||
| Квадрат |  |
S = a 2 | |
 |
S = 4r 2 | ||
 |
|||
 |
|||
| Ромб |  |
||
 |
|||
 |
|||
 |
|||
 |
|||
| Трапеция |  |
||
 |
S = m h | ||
 |
|||
 |
|||
| Дельтоид |  |
S = ab sin φ | |
 |
 |
||
 |
|||
 |
|||
| Произвольный выпуклый четырёхугольник |  |
||
| Вписанный четырёхугольник |  |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
,
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
|
|
|
|
|
|
| Параллелограмм | |
|
|
|
|
|
|
| Квадрат | |
|
S = a 2
где |
|
S = 4r 2 |
|
|
|
|
| Ромб | |
|
|
|
|
|
|
|
|
|
|
| Трапеция | |
|
|
|
|
|
|
|
|
| Дельтоид | |
|
|
|
где |
|
|
|
|
| Произвольный выпуклый четырёхугольник | |
|
|
| Вписанный четырёхугольник | |
|
| Прямоугольник |
|
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Квадрат
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
Ромб
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
Дельтоид
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
Произвольный выпуклый четырёхугольник
φ – любой из четырёх углов между ними
Вписанный четырёхугольник
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
,
что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Нахождение площади выпуклого четырехугольника: формула и пример
Выпуклый четырехугольник – это геометрическая фигура, полученная путем соединения на плоскости четырех точек, которые не должны лежать на одной прямой. При этом образованные таким образом стороны не должны пересекаться.
Формула вычисления площади
По диагоналям и углу между ними
Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними.
По четырем сторонам (формула Брахмагупты)
Чтобы воспользоваться формулой, необходимо знать длины всех сторон фигуры. Также вокруг четырехугольника должна быть возможность описать окружность.
p – полупериметр, вычисляется следующим образом:
По радиусу вписанной окружности и сторонам
Если в четырехугольник можно вписать окружность, вычислить его площадь можно, воспользовавшись формулой:
S = p ⋅ r
r – радиус окружности.
Пример задачи
Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.
Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см 2 .
Формула площади четырехугольника
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
(d1, d2 — диагонали четырёхугольника, φ — угол между ними).
Дано: ABCD — выпуклый четырёхугольник,
Диагонали выпуклого четырёхугольника ABCD делят его на 4 треугольника.
[spoiler title=”источники:”]
[/spoiler]
§3. Площади четырёхугольников
В школьном учебнике выведены следующие формулы площади параллелограмма:
`S=a*h_a=b*h_b`, (6)
`S=a*bsinvarphi` (7)
Где `a` и `b` – стороны параллелограмма, `h_a` и `h_b` – высоты к ним, `varphi` – величина угла между сторонами параллелограмма.
Докажем теорему о площади четырёхугольника.
Площадь выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними, т. е
`S=1/2d_1d_2sinalpha` (8)
где `d_1` и `d_2` – диагонали четырёхугольника, `alpha` – величина угла между ними.
`ABCD` – выпуклый четырёхугольник, диагонали которого `AC` и `BD` пересекаются в точке `O` под углом `alpha` (рис. 15). Через вершины `A` и `C` проведём прямые, параллельные диагонали `BD`, а через вершины `B` и `D` проведём прямые, параллельные диагонали `AC`. Проведённые прямые в пересечении образуют параллелограмм со сторонами, равными диагоналям `BD` и `AC`, и углом `alpha`. Площадь параллелограмма равна `AC*BD*sinalpha`, а площадь четырёхугольника `ABCD` равна, как легко видеть, половине его площади, т. е.
`S_(ABCD)=1/2AC*BD*sinalpha`.
Площадь ромба равна половине произведения его диагоналей. Это сразу следует из доказанной формулы, т. к. диагонали ромба перпендикулярны.
Найти площадь параллелограмма, стороны которого равны `a` и `b` `(a!=b)`, а угол между диагоналями равен `alpha(alpha<90^@)`.
Пусть `O` – точка пересечения диагоналей параллелограмма `ABCD` (рис. 16), `AB=a`, `AD=b`. Обозначим `BD=2x`, `AC=2y`.
Применим теорему косинусов к треугольникам`AOB` и `AOD` (заметим, что `/_AOD=180^@-alpha)`, будем иметь: `a^2=x^2+y^2-2xycosalpha`, `b^2=x^2+y^2+2xycosalpha`. По теореме 3 площадь `S` параллелограмма `ABCD` будет равна `1/2AC*BDsinalpha=2xysinalpha`. Заметим, что это выражение легко можно найти, не определяя `x` и `y` из системы. Действительно, из двух уравнений для `x` и `y` получим `b^2-a^2=4xycosalpha`. По условию `b!=a`, следовательно, `cosa!=0` и `xy=(b^2-a^2)/(4cosalpha)`. Выражаем площадь параллелограмма по формуле (8):
`S=2xysinalpha=(b^2-a^2)/2 “tg”alpha`.
Середины сторон выпуклого четырёхугольника `ABCD` являются вершинами другого четырёхугольника (четырёхугольника Вариньона). Доказать, что четырёхугольник Вариньона – параллелограмм и его площадь равна половине площади `S` четырёхугольника `ABCD`.
1. Проведём диагонали `AC` и `BD`. Середины сторон обозначим `K`, `L`, `M` и `N` (рис. 17). По определению `KL` – средняя линия треугольника `ABC`, по теореме о средней линии `KL“||“AC`, `KL=1/2AC`.
Аналогично, `NM` – средняя линия треугольника `ADC`, `NM“||“AC`, `NM=1/2AC`.
В четырёхугольнике `KLMN` противоположные стороны `KL` и `NM` равны и параллельны, по признаку `KLMN` – параллелограмм.
Если рассмотреть стороны `LM` и `KN`, то точно также установим, что `LM“||“BD“||“KN` и `LM=KN=1/2BD`.
2. Из параллельности `KL“||“AC` и `KN“||“BD` следует, что угол `LKN` параллелограмма `KLMN` равен углу между диагоналями четырёхугольника `ABCD` (обозначим угол `alpha`).
Имеем `S_(KLMN)=KL*KNsinalpha=1/2AC*1/2BDsinalpha`, а по теореме 3
`S_(ABCD)=1/2AC*BD*sinalpha`.
Из этого следует `S_(KLMN)=1/2S_(ABCD)`, ч. т. д.
Рассмотрим несколько задач, где определяется или используется площадь трапеции. Напомним,
что площадь трапеции равна произведению полусуммы оснований на её высоту, т. е.
`S=(a+b)/2h`. (9)
Найти площадь трапеции, если её основания равны `16` и `44`, а боковые стороны равны `17` и `25`.
Через вершину `C` проведём `CK“||“BA` (рис. 18). `ABCK` – параллелограмм, его противоположные стороны равны, поэтому в треугольнике `KCD` определяются все стороны: `KC=AB=25`, `CD=17`, `KD=AD-BC=28`.
По формуле Герона вычисляем площадь этого треугольника: `p=36`, `S_(KCD)=210`.
С другой стороны, `S_(KCD)=1/2KD*CF`, если `CF_|_AD`. Отсюда находим `CF=(2S_(KCD))/(KD)=15` и вычисляем площадь трапеции
`S_(ABCD)=1/2(BC+AD)CF=450`.
Отрезок длины `m`, параллельный основаниям трапеции, разбивает её на две трапеции (рис. 19). Найти отношение площадей этих трапеций, если основания трапеции равны `a` и `b` `(b < a)`.
Пусть `BC=b`, `AD=a` и `MN=m`, и `MN“||“AD`. Проведём `CE“||“BA` и `NF“||“BA`, а также `CK_|_MN` и `NP_|_AD`. Обозначим `CK=h_1`, `NP=h_2`. Далее, т. к. `CE“||“NF`, то `/_ECN=/_FND`, а из `MN“||“AD` следует `/_ENC=/_FDN`. Следовательно, треугольники `ECN` и `FND` имеют по два равных угла, они подобны. Из подобия имеем `(EN)/(FD)=(CN)/(ND)`. Прямоугольные треугольники `KCN` и `PND` также подобны и `(CK)/(NP)=(CN)/(ND)`, поэтому `(EN)/(FD)=(CK)/(NP)`, т. е. `(m-b)/(a-m)=(h_1)/(h_2)`. Если `S_1` и `S_2` – площади трапеций `MBCN` и `AMND`, то
`S_1=1/2(b+m)h_1`, `S_2=1/2(a+m)h_2`
и
`(S_1)/(S_2)=((m+b)h_1)/((a+m)h_2)=(m^2-b^2)/(a^2-m^2`.
Утверждение.
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними:
![[S = frac{1}{2}d_1 d_2 cdot sin varphi ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-87d40725483840edc5f5fddfe1fd209c_l3.png "Rendered by QuickLaTeX.com")
(d1, d2 — диагонали четырёхугольника, φ — угол между ними).
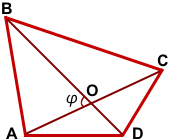Дано: ABCD — выпуклый четырёхугольник,
AC∩BD=O, AC=d1, BD=d2, ∠AOB=φ
Доказать:
![[S_{ABCD} = frac{1}{2}d_1 d_2 cdot sin varphi ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-f2a1203c040984b7b2109e689ee1c3c4_l3.png "Rendered by QuickLaTeX.com")
Доказательство:
Диагонали выпуклого четырёхугольника ABCD делят его на 4 треугольника.
Площадь каждого из треугольников равна половине произведения его сторон на синус угла между ними:
![[S_{Delta AOB} = frac{1}{2} cdot AO cdot BO cdot sin angle AOB;]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-c3138406e01fdf2d96b0e79fbbe63b24_l3.png "Rendered by QuickLaTeX.com")
![[S_{Delta BOC} = frac{1}{2} cdot BO cdot CO cdot sin angle BOC;]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-015364bb5ddb553ba204268d71a05b8b_l3.png "Rendered by QuickLaTeX.com")
![[S_{Delta COD} = frac{1}{2} cdot CO cdot DO cdot sin angle COD;]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-601ebe8b438d5c37e2c650bc3f5d0fd7_l3.png "Rendered by QuickLaTeX.com")
![[S_{Delta AOD} = frac{1}{2} cdot AO cdot DO cdot sin angle AOD.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-267f91d05721f89f18b48aba8d260dc5_l3.png "Rendered by QuickLaTeX.com")
∠BOC=180°-∠AOB=180°-φ (как смежные).
∠COD=∠AOB=φ,
∠AOD=∠BOC=180°-φ (как вертикальные).
sin (180°-φ)=sin φ.
Отсюда
![[S_{Delta AOB} = frac{1}{2} cdot AO cdot BO cdot sin varphi ;]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-6cd8fd6bb964b47abc7a5aca9eb892e2_l3.png "Rendered by QuickLaTeX.com")
![[S_{Delta BOC} = frac{1}{2} cdot BO cdot CO cdot sin varphi ;]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-053504882344c365d945b29155cbef20_l3.png "Rendered by QuickLaTeX.com")
![[S_{Delta COD} = frac{1}{2} cdot CO cdot DO cdot sin varphi ;]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-afa7b2bb3de14d87617395b99c64285f_l3.png "Rendered by QuickLaTeX.com")
![[S_{Delta AOD} = frac{1}{2} cdot AO cdot DO cdot sin varphi .]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-ba81e8e5ac001a6bc99a59a5812478c0_l3.png "Rendered by QuickLaTeX.com")
Таким образом,
![[S_{ABCD} = S_{Delta AOB} + S_{Delta BOC} + S_{Delta COD} + S_{Delta AOD} = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-ba18db460256f09c621d0ebee35a2c4a_l3.png "Rendered by QuickLaTeX.com")
![[= frac{1}{2} cdot sin varphi (AO cdot BO + BO cdot CO + CO cdot DO + AO cdot DO) = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3ff0db582c3a7593e31802b3e4b7bdf4_l3.png "Rendered by QuickLaTeX.com")
![[= frac{1}{2} cdot sin varphi ((AO cdot BO + BO cdot CO) + (CO cdot DO + AO cdot DO)) = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-31834c0a92e6a22eace5c5691386a511_l3.png "Rendered by QuickLaTeX.com")
![[= frac{1}{2} cdot sin varphi (BO(AO + CO) + DO(CO + AO)) = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-cb4645d1734076c689ef0ff45c785aa6_l3.png "Rendered by QuickLaTeX.com")
![[= frac{1}{2} cdot sin varphi (AO + CO)(BO + DO) = frac{1}{2} cdot sin varphi cdot AC cdot BD = ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-3398c6a832b972673fb812cc137b13ad_l3.png "Rendered by QuickLaTeX.com")
![[= frac{1}{2} cdot d_1 cdot d_2 cdot sin varphi .]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-2707bd74c5e88820ad784214832a18ea_l3.png "Rendered by QuickLaTeX.com")
Что и требовалось доказать.
