Как найти площадь выпуклого многоугольника

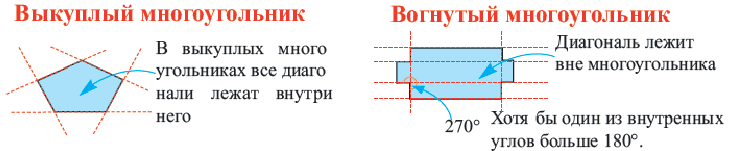
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Определения[править | править код]

Существует множество эквивалентных определений:

• многоугольник является выпуклым, если часть плоскости, им ограниченная (плоский многоугольник) является выпуклым множеством;
• многоугольник будет выпуклым, если для любых двух точек внутри него соединяющий их отрезок полностью лежит в нём;
• многоугольник, для которого продолжения сторон не пересекают других его сторон;
• многоугольник без самопересечений, каждый внутренний угол которого не более 180°;
• многоугольник, все диагонали которого полностью лежат внутри него;
• выпуклая оболочка конечного числа точек на плоскости;
• ограниченное множество, являющееся пересечением конечного числа замкнутых полуплоскостей.

Примеры[править | править код]

• Любой треугольник является выпуклым.

Площадь выпуклого многоугольника[править | править код]

, где .

Вариации и обобщения[править | править код]

• Выпуклое множество
• Аналогом выпуклого многоугольника в трёхмерном евклидовом пространстве является выпуклый многогранник.

См. также[править | править код]

• Выпуклое тело
• Выпуклая оболочка
• Симплекс

Содержание:

Изучив материал этой лекции, вы узнаете формулу, с помощью которой можно найти сумму углов выпуклого многоугольника.

• Вы расширите свои представления о такой знакомой вам величине, как площадь.
• Вы научитесь находить площадь параллелограмма, треугольника, трапеции.

Определение многоугольников

Рассмотрим фигуру, состоящую из точек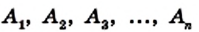

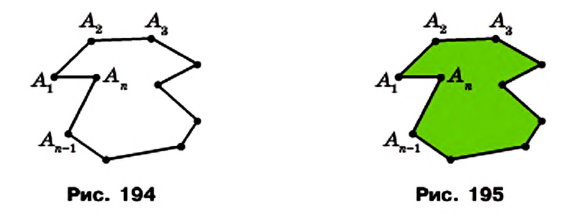
Фигура, образованная этими отрезками, ограничивает часть плоскости, выделенную на рисунке 195 зеленым цветом. Эту часть плоскости вместе с отрезками 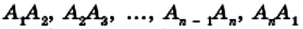 называют многоугольником. Точки 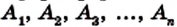называют вершинами многоугольника, а указанные выше отрезки — сторонами многоугольника.

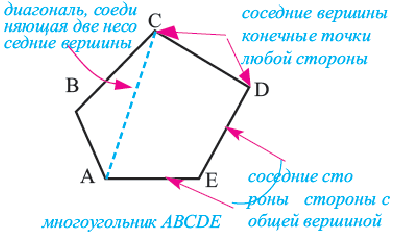
Стороны, являющиеся соседними отрезками, называют соседними сторонами многоугольника. Вершины, являющиеся концами одной стороны, называют соседними вершинами многоугольника.

Две соседние стороны многоугольника образуют угол многоугольника. Например, на рисунке 196  — углы многоугольника, а не является углом многоугольника.

Многоугольник называют по количеству его углов: треугольник, четырехугольник, пятиугольник и т. п.

Многоугольник обозначают по его вершинам. Например, на рисунке 197 изображен пятиугольник ABCDE. В обозначении многоугольника буквы, стоящие рядом, соответствуют соседним вершинам. Например, пятиугольник, изображенный на рисунке 197, можно обозначить еще и так: CDEAB, EABCD, EDCBA и т. д.

Периметром многоугольника называют сумму длин всех его сторон.

Отрезок, соединяющий несоседние вершины многоугольника, называют диагональю. Например, на рисунке 198 отрезок АЕ — диагональ шестиугольника ABCDEF.

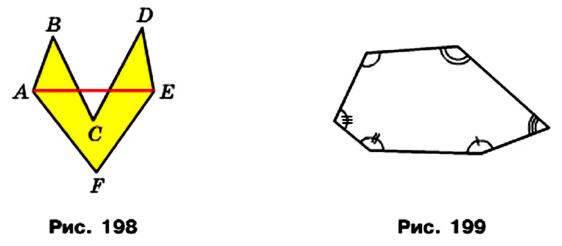
На рисунке 199 изображен многоугольник, все углы которого меньше развернутого. Такой многоугольник называют выпуклым. Из сказанного следует, что любой треугольник является выпуклым многоугольником. Заметим, что многоугольники, изображенные на рисунках 196-198, не являются выпуклыми.

Выпуклый многоугольник обладает такими свойствами:

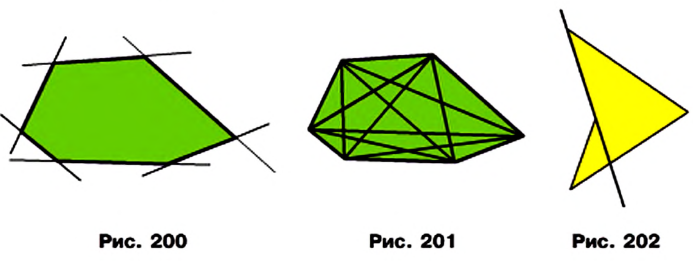
1. выпуклый многоугольник расположен в одной полуплоскости относительно любой прямой, содержащей его сторону (рис. 200);
2. выпуклый многоугольник, отличный от треугольника, содержит любую свою диагональ (рис. 201).

Если многоугольник не является выпуклым, то он такими свойствами не обладает (рис. 198, 202).

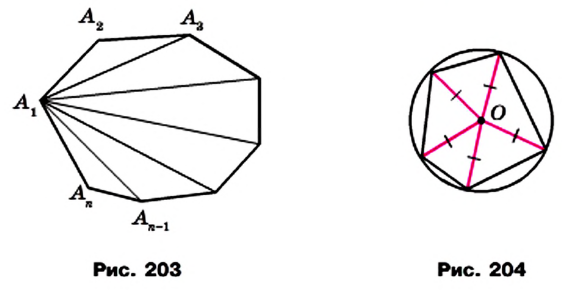
Теорема 19.1. Сумма углов выпуклого n-угольника равна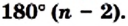

Доказательство. Для случая n = 3 теорема была доказана в 7 классе (теорема 16.1).

Пусть 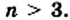 На рисунке 203 изображен выпуклый n-угольник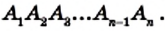

Докажем, что сумма всех его углов равна 180° (n-2).

Проведем все его диагонали, выходящие из вершины 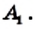Эти диагонали разбивают данный многоугольник на (n – 2) треугольника. Сумма всех углов этих треугольников равна сумме углов n-угольника. Поскольку сумма углов каждого треугольника равна 180°, то искомая сумма равна 180° (n – 2). 

Отметим, что эта теорема справедлива и для любого многоугольника, не являющегося выпуклым.

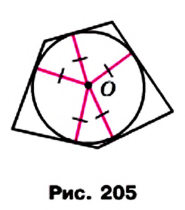
Определение. Окружность называют описанной около многоугольника, если она проходит через все его вершины.

На рисунке 204 изображена окружность, описанная около многоугольника. В этом случае также говорят, что многоугольник вписан в окружность.

Центр окружности, описанной около многоугольника, равноудален от всех его вершин. Следовательно, этот центр принадлежит серединным перпендикулярам всех сторон многоугольника, вписанного в окружность.

Около многоугольника можно описать окружность, если существует точка, равноудаленная от всех его вершин. Следовательно, если серединные перпендикуляры всех сторон многоугольника пересекаются в одной точке, то около такого многоугольника можно описать окружность.

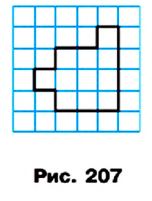
Определение. Окружность называют вписанной в многоугольник, если она касается всех его сторон.

На рисунке 205 изображена окружность, вписанная в многоугольник. В этом случае также говорят, что многоугольник описан около окружности.

Центр окружности, вписанной в многоугольник, равноудален от всех его сторон. Следовательно, этот центр принадлежит биссектрисам всех углов многоугольника, описанного около окружности.

Понятие площади многоугольника. Площадь прямоугольника

С такой величиной, как площадь, вы часто встречаетесь в повседневной жизни: площадь квартиры, площадь дачного участка, площадь поля и т. п.

Опыт подсказывает вам, что равные земельные участки имеют равные площади, что площадь квартиры равна сумме площадей всех ее помещений (комнат, кухни, коридора и т. д.).

Вы знаете, что площади земельных участков измеряют в сотках (арах) и гектарах; площади регионов и государств — в квадратных километрах; площадь квартиры — в квадратных метрах.

На этих практических знаниях о площади основывается определение площади многоугольника.

Определение. Площадью многоугольника называют положительную величину, которая обладает следующими свойствами:

1. равные многоугольники имеют равные площади;
2. если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
3. за единицу измерения площади принимают единичный квадрат, то есть квадрат со стороной, равной единице измерения длины.

Измерить площадь многоугольника — это значит сравнить его площадь с площадью единичного квадрата. В результате получают числовое значение площади данного многоугольника. Это число показывает, во сколько раз площадь данного многоугольника отличается от площади единичного квадрата.

Например, если клетку вашей тетради принять за единичный квадрат, то площадь многоугольника, изображенного на рисунке 207, будет равна 11 квадратным единицам (кратко записывают: 11 ед.²). 

Обычно для нахождения площади используют формулы, то есть вычисляют площадь многоугольника по определенным элементам (сторонам, диагоналям, высотам и т. д.). Некоторые из формул вы уже знаете. Например, вы неоднократно применяли формулу S = ab, где S — площадь прямоугольника, а и b — длины его соседних сторон.

Для доказательства этой формулы потребуется следующая лемма.
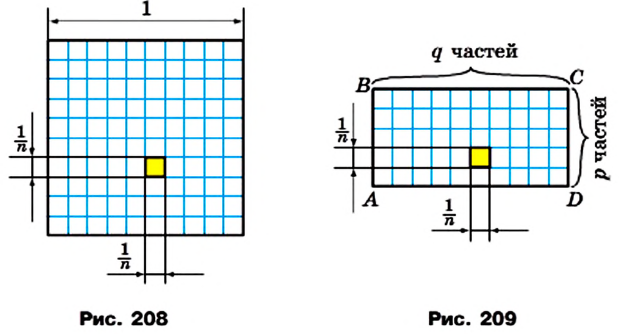
Лемма. Площадь квадрата со стороной 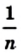ед. (n — натуральное число) равна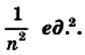

Доказательство. Рассмотрим единичный квадрат и разделим его на 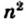равных квадратов со стороной 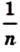(рис. 208).
Из определения площади многоугольника (свойство 1) следует, что все эти квадраты имеют равные площади. По свойству 2 сумма площадей этих квадратов равна площади единичного квадрата, то есть 1 ед.². Поэтому площадь каждого маленького квадрата равна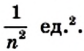

Теорема 20.1. Площадь прямоугольника равна произведению длин его соседних сторон.

Доказательство. На рисунке 209 изображен прямоугольник ABCD, длины соседних сторон которого равны a и b: АВ = а, ВС = b. Докажем для случая, когда а и b — рациональные числа, что площадь S прямоугольника вычисляют по формуле S = ab.

Числа а и b представим в виде обыкновенных дробей с одинаковыми знаменателями:
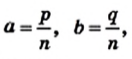 где 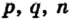– натуральные числа.
Разделим сторону АВ на р равных частей, а сторону ВС — на q равных частей. Через точки деления проведем прямые, параллельные сторонам прямоугольника. Тогда прямоугольник будет разделен на 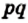равных квадратов со стороной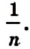 

Согласно лемме площадь каждого квадрата равна 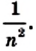Из определения площади (свойство 2) следует, что площадь прямоугольника равна сумме площадей всех квадратов, то есть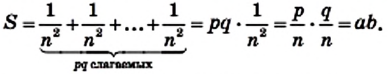
Рассмотрение случая, когда хотя бы одно из чисел а или b является иррациональным, выходит за рамки школьного курса геометрии. 

Определение. Многоугольники, имеющие равные площади, называют равновеликими.

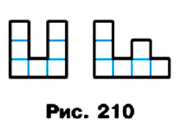
Из определения площади (свойство 1) следует, что все равные фигуры равновелики. Однако не все фигуры, имеющие равные площади, являются равными. Например, на рисунке 210 изображены два многоугольника, каждый из которых составлен из семи единичных квадратов. Эти многоугольники равновелики, но не равны.

Площадь параллелограмма

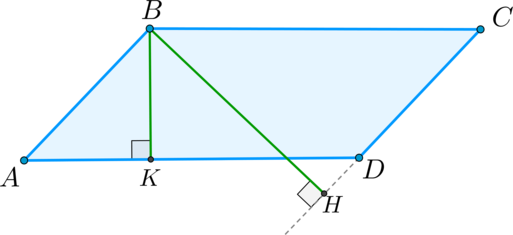
Теорема 21.1. Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.

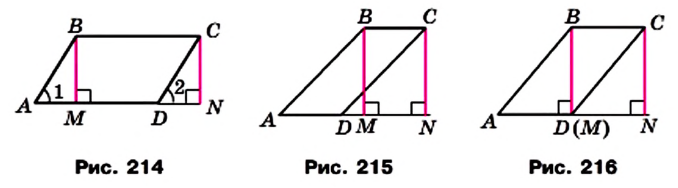
Доказательство. На рисунке 214 изображены параллелограмм ABCD, площадь которого равна S, и его высота ВМ. Докажем, что S = ВС • ВМ.

Проведем высоту CN. Легко показать (сделайте это самостоятельно), что четырехугольник MBCN — прямоугольник. Покажем, что он равновелик данному параллелограмму.

Площадь параллелограмма равна сумме площадей треугольника АВМ и трапеции MBCD. Площадь прямоугольника равна сумме площадей указанной трапеции и треугольника DCN. Однако треугольники АВМ и DCN равны по гипотенузе и острому углу (отрезки АВ и CD равны как противолежащие стороны параллелограмма, углы 1 и 2 равны как соответственные при параллельных прямых АВ и DC и секущей AD). Значит, эти треугольники равновелики. Отсюда следует, что параллелограмм ABCD и прямоугольник MBCN равновелики.

По теореме 20.1 площадь прямоугольника MBCN равна произведению длин сторон ВС и ВМ. Тогда S = ВС • ВМ, где S — площадь параллелограмма ABCD.

Для завершения доказательства надо рассмотреть случаи, когда основание М высоты ВМ не будет принадлежать стороне AD (рис. 215) или совпадет с вершиной D (рис. 216). И в этом случае параллелограмм ABCD и прямоугольник MBCN будут равновеликими. Докажите этот факт самостоятельно. 

Если обозначить длины стороны параллелограмма и проведенной к ней высоты соответственно буквами а и h, то площадь S параллелограмма вычисляют по формуле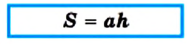 

Площадь треугольника

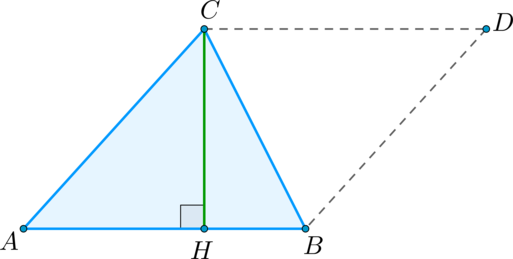
Теорема 22.1. Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.

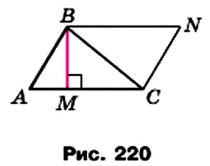
Доказательство. На рисунке 220 изображены треугольник АВС, площадь которого равна S, и его высота ВМ. Докажем, что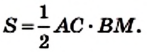
Через вершины В и С треугольника проведем прямые, параллельные сторонам АС и АВ соответственно (рис. 220). Пусть эти прямые пересекаются в точке N. Четырехугольник ABNC — параллелограмм по определению. Треугольники АВС и NCB равны (докажите это самостоятельно). Следовательно, равны и их площади. Тогда площадь треугольника АВС равна половине площади параллелограмма ABNC. Высота ВМ треугольника АВС является также высотой параллелограмма
ABNC. Отсюда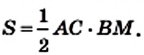

Если воспользоваться обозначениями для высот и сторон треугольника АВС, то согласно доказанной теореме имеем:

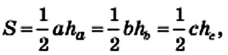
где S — площадь треугольника.   

Следствие. Площадь прямоугольного треугольника равна половине произведения его катетов.    

Докажите эту теорему самостоятельно.   

Пример №1

Докажите, что площадь ромба равна половине произведения его диагоналей.

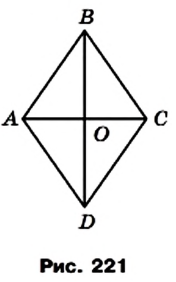
Решение:

На рисунке 221 изображен ромб ABCD, площадь которого равна S. Его диагонали АС и BD пересекаются в точке О. Докажем, что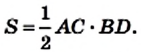
Поскольку диагонали ромба перпендикулярны, то отрезки АО и СО являются высотами треугольников BAD и BCD соответственно. Тогда можно записать:

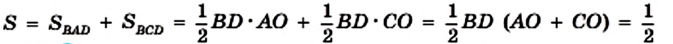
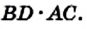
Площадь трапеции

Теорема 23.1. Площадь трапеции равна произведению полусуммы ее оснований и высоты.

Доказательство. На рисунке 224 изображена трапеция ABCD (AD||BC), площадь которой равна S. Отрезок CN — высота этой трапеции. Докажем, что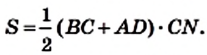

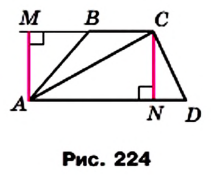
Проведем диагональ АС и высоту AM трапеции. Отрезки AM и CN являются высотами треугольников АВС и ACD соответственно.

Имеем:

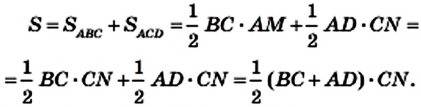
Если обозначить длины оснований трапеции и ее высоты соответственно буквами 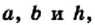то площадь S трапеции вычисляют по формуле

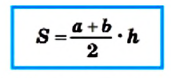
Следствие. Площадь трапеции равна произведению ее средней линии и высоты.

Равносоставленные и равновеликие многоугольники

Если некоторый многоугольник можно разрезать на части и составить из них другой многоугольник, то такие два многоугольника называют равносоставленными.

Например, если прямоугольник разрезать вдоль его диагонали (рис. 228), то получим два равных прямоугольных треугольника, из которых можно составить равнобедренный треугольник (рис. 229). Фигуры на рисунках 228 и 229 — равно составленные.

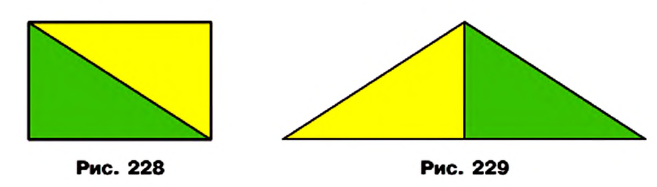
Очевидно, что равносоставленные многоугольники являются равновеликими. Этот факт применяют при доказательстве теорем и решении задач. Например, доказывая теорему 21.1, мы фактически разрезали параллелограмм на треугольник АВМ и трапецию MBCD, из которых составили прямоугольник MBCN (см. рис. 215).

Если треугольник разрезать вдоль средней линии, то из полученных треугольника и трапеции можно составить параллелограмм (рис. 230).

Легко установить (сделайте это самостоятельно), что такое разрезание треугольника приводит к еще одному доказательству теоремы о площади треугольника (теорема 22.1). Этой же цели служит разрезание треугольника на части, из которых можно составить прямоугольник (рис. 231).

Евклид в своей знаменитой книге «Начала» формулирует теорему Пифагора так:

«Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах».

Если показать, что можно разрезать квадраты, построенные на катетах, на части и составить из этих частей квадрат со стороной, равной гипотенузе, то тем самым будет доказана теорема Пифагора.

На рисунке 232 показан один из возможных способов такого разрезания. Квадраты, построенные на катетах, разрезаны на части, площади которых равны 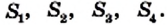 Из этих частей сложен квадрат, построенный на гипотенузе.

Из определения площади многоугольника следует, что равносоставленные многоугольники являются равновеликими. Но совсем неочевидной является такая теорема.

Теорема. Любые два равновеликих многоугольника являются равносоставленными.

Впервые этот факт доказал в 1832 г. венгерский математик Фаркаш Бойяи. Позднее немецкий математик Пауль Гервин нашел другое доказательство. Поэтому эту теорему называют теоремой Бойяи—Гервина.

Теорема Чевы

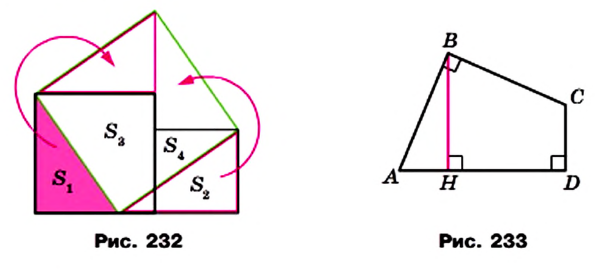
На сторонах ВС, СА и АВ треугольника АВС отметим произвольные точки (рис. 234). Каждый из отрезков АЛ,, BBV СС, называют чевианой треугольника АВС. Такое название связано с именем итальянского инженера и математика Джованни Чевы (1648-1734), открывшего удивительную теорему.

Если точки 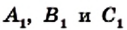выбраны так, что чевианы являются биссектрисами, либо медианами, либо высотами остроугольного треугольника, то эти чевианы пересекаются в одной точке.

Если три прямые пересекаются в одной точке, то их называют конкурентными.

Теорема Чевы дает общий критерий конкурентности произвольных трех чевиан.

Теорема. Для того чтобы, чевианы 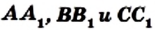треугольника АВС пересекались в одной точке, необходимо и достаточно, чтобы выполнялось равенство

Доказательство. Докажем сначала необходимое условие конкурентности: если чевианы 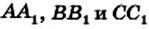пересекаются в одной точке, то выполняется равенство (*).

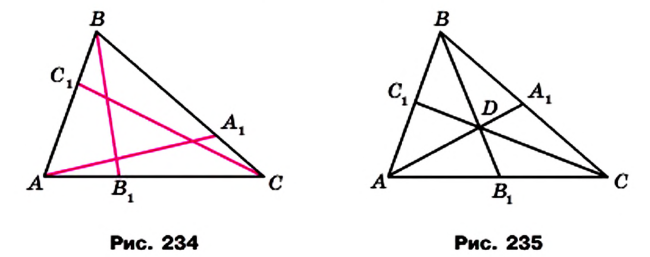
Воспользовавшись результатом ключевой задачи 757, можно записать (рис. 235):

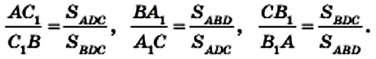
Перемножив записанные равенства, получим равенство (*).

Докажем теперь достаточное условие конкурентности: если выполняется равенство (*), то чевианы 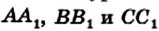пересекаются в одной точке.

Пусть чевианы 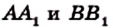пересекаются в точке D, а чевиана, проходящая через вершину С и точку D, пересекает сторону АВ в некоторой точке 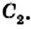Из доказанного выше можно записать:

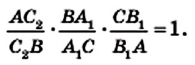
Сопоставляя это равенство с равенством (*), приходим к выводу, что 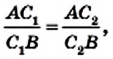 то есть точки 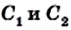делят отрезок АВ в одном и том же отношении, а значит, эти точки совпадают. Следовательно, прямая CD пересекает сторону АВ в точке

Напомню:

Сумма углов выпуклого n-угольника
Сумма углов выпуклого n-угольника равна 180° (n – 2).

Окружность, описанная около многоугольника
Окружность называют описанной около многоугольника, если она проходит через все его вершины.

Окружность, вписанная в многоугольник
Окружность называют вписанной в многоугольник, если она касается всех его сторон.

Площадь многоугольника
Площадью многоугольника называют положительную величину,
которая обладает следующими свойствами:

1. равные многоугольники имеют равные площади;
2. если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников;
3. за единицу измерения площади принимают единичный квадрат, то есть квадрат со стороной, равной единице измерения длины.

Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон.

Равновеликие многоугольники
Многоугольники, имеющие равные площади, называют равновеликими.

Площадь параллелограмма
Площадь параллелограмма равна произведению его стороны и высоты, проведенной к этой стороне.

Площадь треугольника
Площадь треугольника равна половине произведения его стороны и проведенной к ней высоты.

Площадь прямоугольного треугольника
Площадь прямоугольного треугольника равна половине произведения его катетов.

Площадь трапеции

• Площадь трапеции равна произведению полусуммы ее оснований и высоты.
• Площадь трапеции равна произведению ее средней линии и высоты.

Ломанная линия и многоугольники

Ломаная линия состоит из таких нескольких последовательно-соединенных отрезков: конец первого является началом второго, конец второго является началом третьего и т.д. Если конечная точка последнего отрезка совпадает с начальной точкой первого отрезка, то ломаная называется замкнутой. Многоугольник – это фигура, образованная замкнутой ломаной линией, в которой смежные отрезки не лежат на одной прямой, а несмежные – не пересекаются.

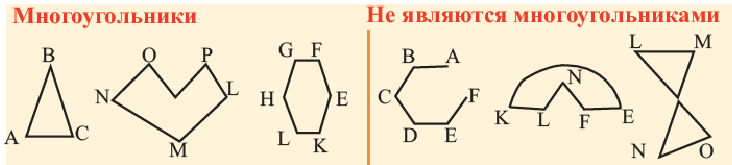
• Многоугольник – это плоская фигура.
• Стороны состоят из конечного числа отрезков.
• Многоугольник это замкнутая фигура, делящая плоскость на 2 части: внутреннюю замкнутую область и внешнюю бесконечную область.
• Многоугольник обозначают буквами, указывающими его вершины.

Многоугольники бывают выпуклые и вогнутые. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой содержащей его сторону. Если не лежит в одной полуплоскости – вогнутым.

Многоугольник называется правильным, если у него все стороны все углы конгруэнтны.

В многоугольнике количество вершин, сторон и углов одинаковые. Многоугольник с – сторонами называют еще и – угольным.

Соответственно количеству сторон, многоугольники называются треугольными, четырехугольными, пятиугольными, шестиугольными т.д. Из любой вершины выпуклого 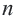– угольника выходят 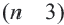диагонали.

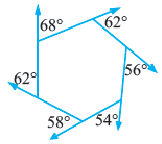
Внутренние и внешние углы многоугольника

Угол, образованный двумя сторонами, исходящими из данной вершины называется внутренним углом при данной’ вершине выпуклого многоугольника. Угол, смежный с внутренним углом многоугольника называется внешним. Сумма внутренних и внешних углов (взятых по одному при каждой вершине) многоугольника при любой вершине равна .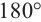

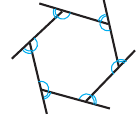
Теорема 1. Сумма внутренних углов выкуплого 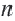– угольник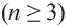а равна .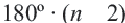

Следствие: Каждый внутренний угол правильного 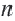– угольника равен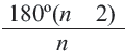

Теорема 2. Сумма внешних углов выкуплого многоугольника равен .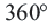

Следствие 2. Каждый внешний угол правильного 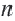– угольника равен .

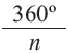Пример №2

Один из внешних углов правильного многоугольника равен .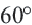

a) найдите градусную меру внутреннего угла многоугольника;

b) найдите число сторон многоугольника.

Решение: а) ;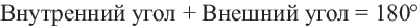

Внутренний угол:

b)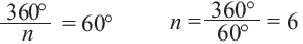

Многоугольники вписанные в окружность и описанные около окружности

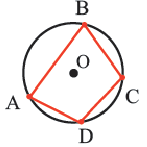
Определение 1. Многоугольник называется вписанным в окружность, если все его вершины лежат на окружности, а окружность называется описанной около многоугольника. На рисунке треугольник 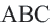вписан в окружность.

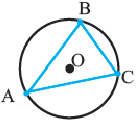
Определение 2. Многоугольник называется описанным около окружности, если все его стороны касаются окружности, а окружность называется вписанной в многоугольник. На рисунке четырехугольник описан около окружности.

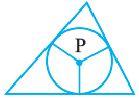
Окружность, вписанная в треугольник и описанная около нее

Теорема 1. В любой треугольник можно вписать окружность. Центром этой окружности будет точка пересечения биссектрис углов треугольника.

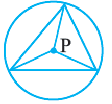
Теорема 2. Около любого треугольника можно описать окружность. Центром этой окружности будет точка пересечения серединных перпендикуляров к сторонам треугольника.

Теорема 3. Если в окружность вписан прямоугольный треугольник, то гипотенуза является диаметром этой окружности.

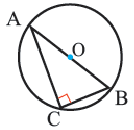
Обратная теорема. Если сторона треугольника, вписанного в окружность, является диаметром, то этот треугольник – прямоугольный.

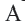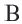Доказательство 1-ой теоремы (текстовое). Проведем биссектрисы углов и треугольника 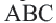и точку пересечения обозначим буквой . Произвольная точка, взятая на биссектрисе находится на одинаковом расстоянии от сторон угла. Поэтому 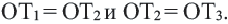Точка находится и на биссектрисе угла 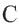(почему?). Нарисуем окружность с центром в точке и радиусом 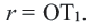Так как стороны треугольника перпендикулярны радиусам 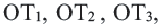то в точках 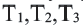они касаются окружности. А значит, эта окружность является вписанной в треугольник.

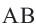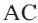Доказательство 2-ой теоремы. Через середины сторон и треугольника 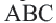проведем перпендикуляры и точку их пересечения обозначим буквой . По свойству серединного перпендикуляра к отрезку 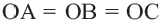. Так как 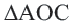равнобедренный, то точка находится и на серединном перпендикуляре стороны 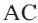. Окружность с центром в точке и радиусом 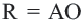, пройдя через все вершины треугольника, будет описанной около нее.

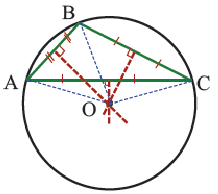
Замечание: Около данного треугольника можно описать только одну окружность. В данную окружность можно вписать бесконечное количество треугольников.

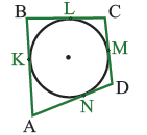
Свойства четырехугольников, вписанных в окружность и описанного около нее

В отличие от треугольников, не во всякий четырехугольник можно вписать или описать окружность.

Теорема 4. В любом описанном четырехугольнике суммы противоположных сторон равны.

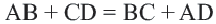
Обратная теорема. Если суммы противоположных сторон четырехугольника равны, то в этот четырехугольник можно вписать окружность.

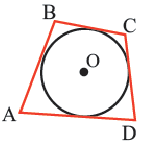
Теорема 5. Сумма двух противоположных углов четырехугольника, вписанного в окружность, равна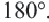

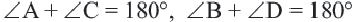
Обратная теорема. Если сумма противоположных углов четырехугольника равна 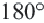, то около этого четырехугольника можно описать окружность.

Доказательство теоремы 4: Пусть точки будут точками касания сторон четырехугольника. По свойству касательных, проведенных из данной точки к окружности,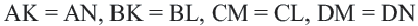

Если сложить почленно эти равенства, получим 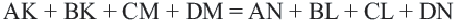или же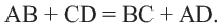

Отношение стороны треугольника, вписанного в окружность, к синусу противолежащего угла равно диаметру этой окружности: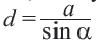

Исследуйте данное доказательство для случая, когда центр окружности расположен внутри треугольника, обсудите и напишите в тетради.

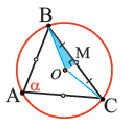
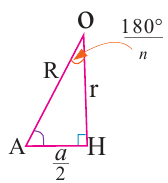
В любой правильный многоугольник можно вписать и описать окружность. Центры этих окружностей совпадут. Биссектрисы углов правильного многоугольника пересекаются в точке и образуют равнобедренные треугольники конгруэнтные показанному на рисунке (по признаку УСУ). Нарисуем окружность радиусом 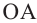с центром в точке 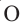. Эта окружность, пройдя через все вершины, будет описанной окружностью. 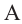окружность с радиусом , касаясь всех сторон многоугольника, будет вписанной окружностью. 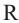– радиус окружности, описанной около правильного 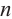-угольника, 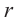-радиус вписанной окружности, 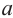-сторона правильного 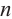-угольника, 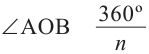– центральный угол

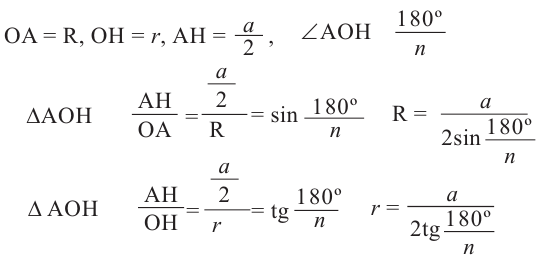
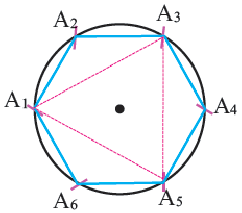
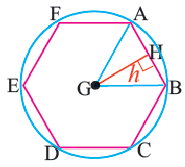
Задача на построение: Постройте правильный шестиугольник.

1. Нарисуйте отрезок , равный стороне правильного шестиугольника.

2. Циркулем нарисуйте окружность, радиус которой равен длине этого отрезка.

3. Не меняя раствора циркуля, разбейте всю окружность на части одинаковой длины и отметьте их точками.

4. Соедините последовательно отмеченные точки. Получится правильный шестиугольник, вписанный в окружность.

Если соединить попарно некоторые вершины правильного шестиугольника , например, вершины , то получится правильный треугольник. Чтобы построить правильный четырехугольник, нужно провести два взаимно перпендикулярных диаметра и последовательно соединить их концы. Если в окружность вписан правильный 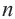– угольник, то отметив точки пересечения серединных перпендикуляров с окружностью, получим точки являющиеся вершинами правильного 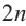-угольника.

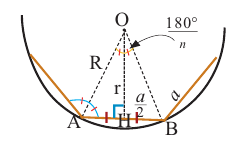
Площадь правильного многоугольника

Центр правильного многоугольника. Центр окружности, описанного около правильного многоугольника или вписанного в него, является центром правильного многоугольника. Центр правильного многоугольника находится на одинаковом расстоянии от всех вершин и всех сторон многоугольника.

Апофема правильного многоугольника. Перпендикуляр, проведенный из центра многоугольника к его стороне, называется апофемой. Апофема правильного многоугольника равна радиусу вписанной окружности.

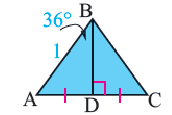
Выполните следующее упражнение по шагам и выведите формулу зависимости площади правильного многоугольника от апофемы.

1. Нарисуйте правильный пятиугольник .

2. Из центра проведите перпендикуляр, делящий сторону пополам.

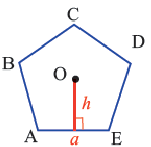
3. Соедините точки и с центром .

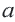4. Выразите площадь треугольника переменными и 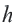. Обратите внимание какому измерению многоугольника соответствует высота треугольника.

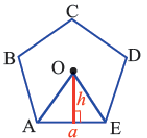
5. Соедините точки с точкой . Сравните площади полученных треугольников.

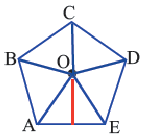
6. Обратите внимание на то, что площадь пятиугольника равна сумме площадей этих треугольников. Площадь пятиугольника:

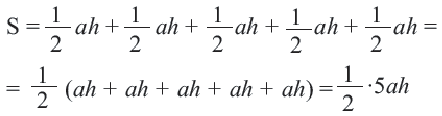7. Какому измерению соответствует выражение 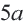? Выразите площадь пятиугольника через его периметр.

Площадь правильного многоугольника:

Соединив центр правильного 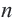-угольника с вершинами, получится 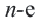количество равнобедренных конгруэнтных треугольников.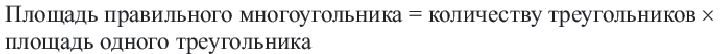

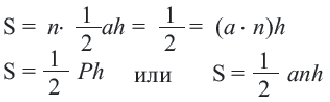
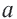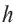-длина стороны многоугольника , -число сторон, -апофема.

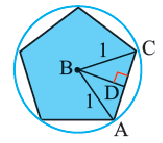
Пример №3

В окружность радиусом равным единице, вписан правильный пятиугольник. Найдите площадь пятиугольника. Решение:

Площадь многоугольника: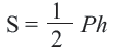

Нужно найти апофему 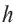и периметр .

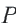Центральный угол 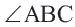равен 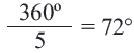. 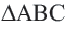– равнобедренный треугольник, а значит его высота 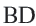является и медианой, и биссектрисой.

Тогда 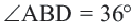. Чтобы найти стороны треугольника , воспользуемся тригонометрическими соотношениями .

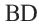– апофема пятиугольника,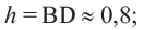

Сторона пятиугольника: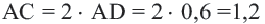

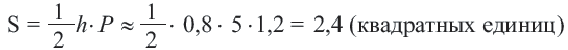
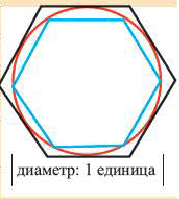
Историческое сведение. В 3-ем веке до н.э. Архимед – древнегреческий ученый, для того, чтобы определить численное значение 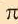, воспользовался периметрами правильных; многоугольников описанных и вписанных в окружность. Пользуясь данным способом исследуйте значение .

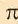1. Принимая за единицу диаметр окружности, найдите периметр вписанного шестиугольника.

2. Покажите, что длина окружности с единичным диаметром равна .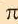

3. Нарисуйте радиус окружности. Найдите периметр описанного шестиугольника.

4. Напишите неравенство: .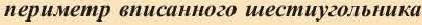

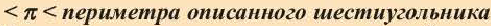Увеличив число сторон многоугольника в 2 раза и продолжая вычисления для 12-ти, а затем для 96-ти угольного многоугольника Архимед, определил, что значения 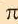больше 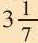, но меньше .

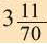Паркетирование

Паркетированием называется покрытие площади фигурами до заполнения всей пустоты.

Если сумма углов при общей вершине многоугольника равна 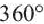, то паркетированием можно покрыть всю пустую часть площади. Паркетирование возможно при помощи правильных треугольников, ромбов (квадратов) и правильных шестиугольников. Однако, при помощи правильных пятиугольников это сделать невозможно, потому что, градусная мера одного угла равна 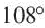, а сумма углов при общей вершине трех пятиугольников 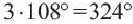, а четырех пятиугольников .

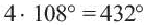Справочный материал по многоугольникам

Многоугольник и его элементы.

Сумма углов выпуклого многоугольника. многоугольник, вписанный в окружность, и многоугольник, описанный около окружности.

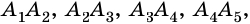
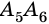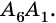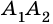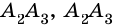Рассмотрим фигуру изображенную на рисунке 213. Она состоит из отрезков   и  При этом отрезки размещены так, что соседние отрезки ( и и и 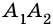) не лежат на одной прямой, а несоседние отрезки не имеют общих точек. Такую фигуру называют многоугольником. Точ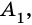ки называют вершинами многоугольника, а отрезки 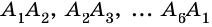– сторонами многоугольника.

Очевидно, что количество вершин многоугольника равно количеству его сторон.

Сумму длин всех сторон многоугольника называют его периметром.

Наименьшее количество вершин (сторон) у многоугольника – три. В этом случае имеем треугольник. Еще одним отдельным видом многоугольника является четырехугольник.

Многоугольник, у которого вершин, называют угольником. На рисунке 213 изображен шестиугольник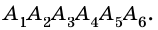 

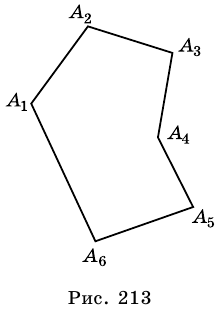
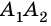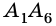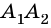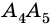Две стороны многоугольника называют соседними, если они имеют общую  вершину. Стороны многоугольника, не имеющие общей вершины, называют несоседними. Например, стороны и – соседние, a  и – несоседние (рис. 213).

Две вершины многоугольника называют соседними, если они принадлежат одной стороне, а вершины многоугольника, не принадлежащие одной стороне, называют несоседними.

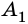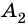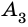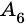Например, вершины и – соседние, и – несоседние (рис. 213).

Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. На рисунке 214 изображены диагонали многоугольника  выходящие из вершины  

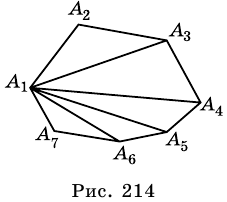
Пример №4

Сколько диагоналей имеет 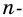угольник?

Решение:

Из каждой вершины 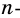угольника выходит  диагонали. Всего вершин 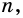 а каждая диагональ повторяется дважды, например 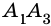и 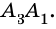Поэтому всего диагоналей у 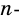угольника будет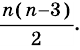 

Ответ.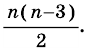

Углы, стороны которых содержат соседние стороны многоугольника, называют углами многоугольника. Пятиугольник 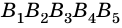имеет углы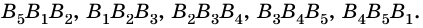

Если каждый из углов многоугольника меньше развернутого, то такой многоугольник называют выпуклым. Если хотя бы один угол многоугольника больше развернутого, то такой многоугольник называют невыпуклым.

Многоугольник 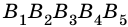 – выпуклый (рис. 215), а многоугольник – невыпуклый (рис. 216), так как угол при вершине 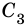больше чем 180°.

Теорема (о сумме углов выпуклого угольника). Сумма углов выпуклого угольника равна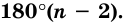

Доказательство:

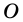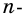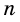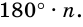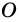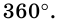Выберем во внутренней области многоугольника произвольную точку и соединим ее со всеми вершинами угольника (рис. 217). Получим треугольников, сумма всех углов которых равна  Сумма углов с вершиной в точке  равна  Сумма углов данного 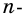угольника равна сумме углов всех треугольников, кроме углов с вершиной в точке  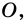то есть: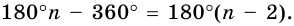

Углы выпуклого многоугольника называют еще его внутренними углами. Угол, смежный с внутренним углом многоугольника, называют внешним углом многоугольника. На рисунке 218 угол — внешний угол многоугольника 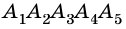– при вершине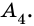

Очевидно, что каждый многоугольник имеет по два внешних угла при каждой вершине. 

Пример №5

Докажите, что сумма внешних углов выпуклого угольника, взятых по одному при каждой вершине, равна 360°.

Решение:

Сумма внутреннего и внешнего углов при каждой вершине многоугольника равна 180°. Поэтому сумма всех внутренних и внешних углов 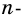угольника равна  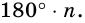Так как сумма внутренних углов равна 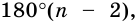то сумма внешних углов равна:

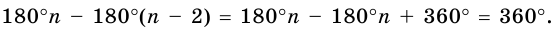
Многоугольник называют вписанным в окружность, если все его вершины лежат на окружности. Окружность при этом называют описанной около многоугольника (рис. 219). 

Около многоугольника не всегда можно описать окружность. Если же это возможно, то центром такой окружности является точка пересечения серединных перпендикуляров к сторонам многоугольника (как и в случае треугольника).

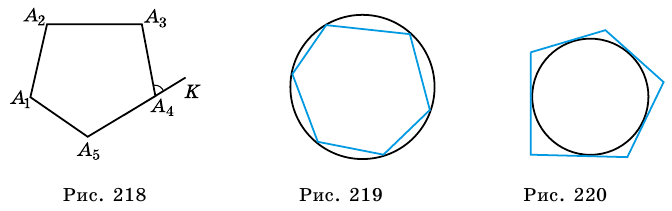
Многоугольник называют описанным около окружности, если все его стороны касаются окружности. Окружность при этом называют вписанной в многоугольник (рис. 220).

Не в каждый многоугольник можно вписать окружность. Если же это возможно, то центром такой окружности является точка пересечения биссектрис внутренних углов многоугольника (как и в случае треугольника).

Многоугольник и его свойства

Вы уже знаете, что такое треугольник и четырёхугольник. Более общим является понятие многоугольника. На рисунке 327 вы видите многоугольник ABCDEF. Он состоит из отрезков АВ, ВС, CD, DE, EFy FA, размещённых таким образом, что смежные отрезки не лежат на одной прямой, а несмежные -не имеют общих точек. Отрезки, из которых состоит многоугольник, называются его сторонами, углы, образованные смежными сторонами, – углами, а вершины этих углов – вершинами многоугольника.

В зависимости от количества вершин (углов либо сторон) многоугольник называется треугольником, четырёхугольником, пятиугольником и т. д. Многоугольник с n вершинами называется n-угольником.

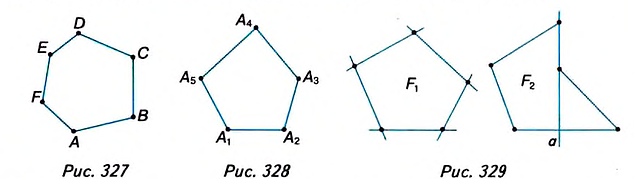
Многоугольник обозначают названиями его вершин, например шестиугольник ABCDEF (рис. 327), пятиугольник 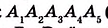(рис. 328). ? | На рисунке 329 вы видите многоугольники 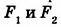. В чём их различие?

Ни одна из прямых, проходящих через стороны многоугольника не пересекает другие его стороны. Он лежит по одну сторону от любой из этих прямых. Такой многоугольник называется выпуклым. Многоугольник 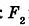не является выпуклым.

В дальнейшем мы будем рассматривать лишь выпуклые многоугольники.

Периметром многоугольника называется сумма длин всех его сторон. Его обозначают буквой Р.

Посмотрите на рисунок 330. В шестиугольнике ABCDEF отрезки AC, AD, АЕ соединяют вершину А с несоседними вершинами. Это – диагонали шестиугольника.

Диагональю n-угольника называется отрезок, который соединяет две несоседние его вершины.

Теорема (о сумме углов n-угольника).

Сумма углов n-угольника равна 180° • (n – 2).

Дано: 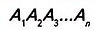— n-угольник (рис. 331), 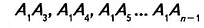— диагонали. Доказать: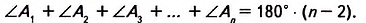

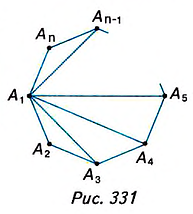
Доказательство. В заданном n-угольнике диагонали 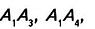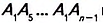выходят из одной вершины 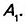Поэтому они разбивают n-угольник на n — 2 треугольников. Сумма всех углов образованных треугольников равна сумме углов данного n-угольника. Поскольку в каждом треугольнике сумма углов равна 180°, то сумма углов данного n-угольника — 180° • (n — 2).

Угол, смежный с углом многоугольника (рис. 332), называется внешним углом многоугольника.

Многоугольники могут быть вписанными в окружность (рис. 333) или описанными около окружности (рис. 334). Попытайтесь дать определения и сравните их с указанными в учебнике.

Многоугольник все вершины которого лежат на окружности, называется вписанным, в эту окружность, а окружность – описанной около этого многоугольника.

Многоугольнику все стороны которого касаются окружности, называется описанным около этой окружности, а окружность – вписанной в этот многоугольник.

Стороны вписанного многоугольника и его диагонали – это хорды окружности. Каждый его угол является вписанным углом (рис. 335).

Стороны описанного многоугольника являются касательными к окружности, а его диагонали – секущими (рис. 336).

1. Геометрическая фигура называется простой, если её можно разбить на конечное количество треугольников. Многоугольник — это простая фигура (см. рис. 330 и 331), а окружность не является простой фигурой (рис. 337). Даже вписав в окружность многоугольник с очень большим количеством сторон, мы только приблизим его контур к окружности. Поэтому в геометрии длину окружности и площадь круга находят другими методами, чем периметр и площадь многоугольника.

2. У вас может возникнуть вопрос: Всегда ли из равенства сторон многоугольника следует равенство его углов и наоборот? Нет, это свойство лишь треугольника. Вы знаете пример четырёхугольника, в котором все стороны равны, а углы — не равны. Это ромб. В прямоугольнике все углы равны, а вот стороны — нет. Среди многоугольников с большим количеством вершин также можно выделить равносторонние многоугольники, в которых не все углы равны (рис. 338), и равноугольные многоугольники, в которых не все стороны равны

Понятие площади

Многоугольник разбивает плоскость на две области – внутреннюю (рис. 345) и внешнюю (рис. 346).

Многоугольник вместе с его внутренней областью называется плоским многоугольником.

Каждый плоский многоугольник (например, многоугольник F на рис. 347) занимает часть плоскости. Если эту часть плоскости выразить некоторым числом, то получим площадь многоугольника. Далее будем говорить «площадь многоугольника», имея в виду, что многоугольник -плоский. Это относится и к другим плоским фигурам.

Площадь обозначают буквой S. Иногда указывают название фигуры, например , а для нескольких фигур – индексы, например 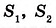и т. д.

На рисунке 348 фигуры 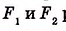равны, поскольку совмещаются наложением. Понятно, что они имеют равные площади. Можем записать: . Для измерения площади фигуры выбирают единицу измерения. Для этого используют квадрат, со стороной равной единице измерения длины. Площадь квадрата со стороной 1 см – это единица измерения площади в квадратных сантиметрах, со стороной 1 м – в квадратных метрах и т. д.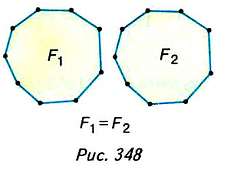

Единицы измерения площади кратко записываем так: 1 см2, а говорим: «один квадратный сантиметр». Говорить «сантиметр в квадрате» -неправильно!

Некоторые единицы измерения площади имеют специальные названия: ар (квадрат со стороной 10м), гектар (квадрат со стороной 100 м) и т. д.

На рисунке 349 вы видите квадрат ABCD со стороной 2 см. Он состоит из четырёх квадратов площадью 1 см2, поэтому его площадь равна 4 см2.

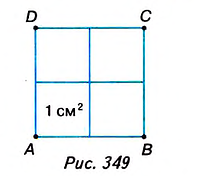
Можем записать: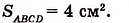

Ясно, что площадь любой фигуры выражается положительным числом. Изменится ли площадь квадрата ABCD, если за единицу измерения принять 1 мм2? Нет, площадь квадрата не изменится, но будет выражена иначе: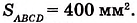

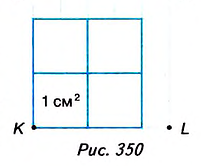
На рисунке 350 длина стороны квадрата KLMN равна 2,5 см. Он вмещает четыре квадрата площадью 1 см2 и ещё 9 маленьких квадратов площадью 0,25 см2. Поэтому 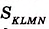= 4 + 9 • 0,25 = 6,25 (см2).

Ясно, что площадь любой фигуры равна сумме площадей частей, из которых она состоит.

Из предыдущих классов вы знаете, что площадь квадрата со стороной а можно вычислить иначе – по формуле площади квадрата:

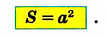
Для квадратов ABCD и KLMN получим: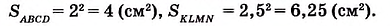

Поскольку 4 см2 < 6,25 см2, то можем записать: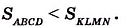

Формулу площади квадрата будем считать основной, поэтому принимаем её без доказательства. Для других фигур формулы площади нужно выводить, исходя из основных свойств площади. Сформулируем их.

Основные свойства площади

1. Площадь каждой фигуры больше нуля.
2. Равные фигуры имеют равные площади.
3. Площадь фигуры равна сумме площадей фигур, из которых она состоит.
4. Единицей измерения площади является площадь квадрата со стороной, равной единице длины.

Основные свойства площади подсказывают способ выведения формул площади.

Для того чтобы вывести формулу площади многоугольника, нужно: либо разбить его на части, формулы площадей которых известны, либо дополнить его до такой фигуры, формула площади которой известна.

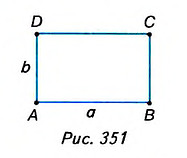
Теорема (о площади прямоугольника).

Площадь прямоугольника равна произведению его смежных сторон.

Дано: ABCD— прямоугольник (рис. 351),

AB=a,AD=b.

Доказать: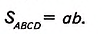

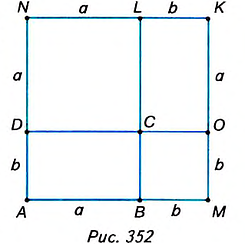
Доказательство. Достроим данный прямоугольник ABCD до квадрата AMKN со стороной о + b (рис. 352). Тогда S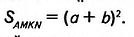

С другой стороны, квадрат AMKNcociom из двух прямоугольников ABCD и OKLC и двух квадратов ВМОС и DNLC. Поэтому, по третьему свойству площади,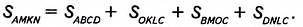

Прямоугольники ABCD и OKLC равны, поскольку равны смежные стороны а и b. Поэтому, по второму свойству площади, 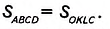Квадраты ВМОС и DNLC имеют соответственно стороны b и а, поэтому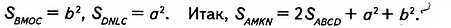

Далее получим:

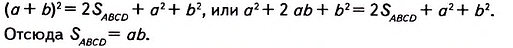
Следствие. Площадь прямоугольного треугольника с катетами а и b равна половине произведения катетов.

Действительно, диагональ АС разбивает прямоугольник ABCD со сторонами а и b (рис. 353) на два равных прямоугольных треугольника ABC и ADC с катетами а и b. Поэтому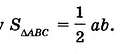

Пример №6

Докажите, что отношение площадей подобных прямоугольных треугольников равно квадрату их коэффициента подобия.

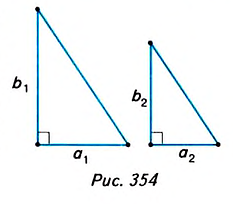
Решение:

Пусть один из заданных прямоугольных треугольников (рис. 354) имеет катеты 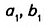и площадь 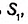, другой — катеты 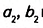и площадь 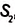, а коэффициент их подобия равен k.

Докажем, что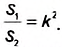

Поскольку треугольники подобны, то 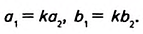Найдём площади треугольников и их отношение:

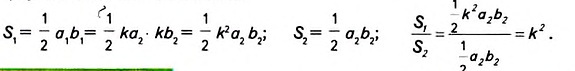
У вас может возникнуть вопрос: Как доказать, что площадь квадрата равна квадрату его стороны? Пусть сторона квадрата ABCD равна а. Возможны два случая: сторону АВ можно разбить на целое число п единичных отрезков (рис. 355); на стороне АВ можно разместить л единичных отрезков, но остаётся ещё отрезок, который короче единичного (рис. 356).

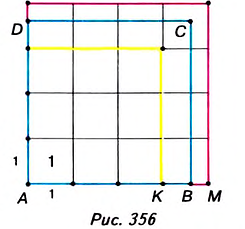
Рассмотрим первый случай (рис. 355). Разобьём сторону АВ на п единичных отрезков (на рисунке их три), тогда о — n • 1 — n. Аналогично разобьём сторону AD. Через точки деления проведём прямые, перпендикулярные АВ и AD. Эти прямые разбивают квадрат ABCD на 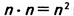равных квадратов площадью 1.

Поэтому .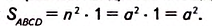

Рассмотрим второй случай (рис. 356). Пусть на отрезке АВ помещается n единичных отрезков и остаётся ещё отрезок длиной меньше 1. Это означает, что отрезок АК из п единичных отрезков меньше отрезка АВ, а отрезок AM из n + 1 единичных отрезков — больше этого отрезка. Получаем неравенство: n < а < n + 1.

Чтобы точнее оценить площадь заданного квадрата, разделим единичный отрезок на т равных частей. Тогда длина каждой части будет равна .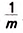

Пусть на отрезке АК их помещается 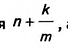, а на отрезке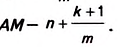

Число а будет лежать в пределах 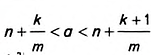а квадрат этого числа — в пределах 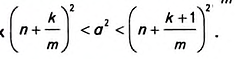Площадь квадрата со стороной АК будет равна 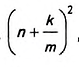, а квадрата со стороной AM – 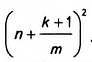Поэтому площадь квадрата ABCD будет лежать в пределах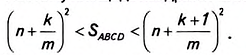

При увеличении количества точек деления число т станет как угодно большим. Площадь квадрата ABCD и квадрат числа а будут лежать в пределах, разность которых как угодно мала: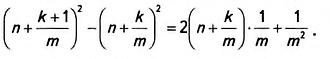

А это возможно лишь в случае, если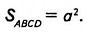

3. Символ S для обозначения площади фигуры происходит от латинского слова superficils, что означает «поверхность».

Параллелограмм и его площадь

Вы уже знаете формулы площадей трёх фигур -квадрата, прямоугольника и прямоугольного треугольника. Выведем формулу площади параллелограмма.

Теорема (о площади параллелограмма).

Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.

Дано: ABCD — параллелограмм (рис. 367), DH— высота, АВ= a, DH= .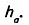

Доказать: .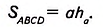

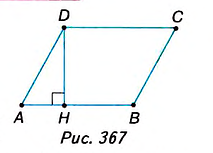
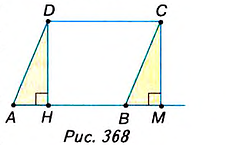
Доказательство. Проведём из вершины С высоту СМ= DH = 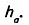(рис. 368). Получили трапецию AMCD. Рассмотрим две пары фигур, из которых она состоит: данный параллелограмм ABCD и ∆ВМС, прямоугольник HMCD и ∆AHD. По третьему свойству площади, 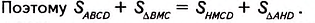∆ВМС= ∆AHD по катету и гипотенузе: СМ= DH как высоты, проведённые к одной стороне АВ параллелограмма, AD — ВС как противоположные стороны параллелограмма. Поэтому, согласно второму свойству площади , 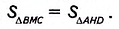. Следовательно, 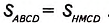. Для прямоугольника HMCD имеем: 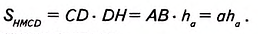Согласно доказанному, площадь данного параллелограмма ABCD равна площади прямоугольника HMCD, поэтому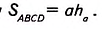

Пример №7

В параллелограмме стороны равны 8 см и 6,4 см, а высота, проведённая к большей стороне, — 6 см. Найдите высоту параллелограмма, проведённую к меньшей его стороне.

Решение:

Пусть ABCD— данный параллелограмм (рис. 369), в котором ab =6,4 см, ВС — 8 см, DM= 6 см.

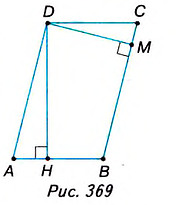
Требуется найти высоту DH.

Площадь параллелограмма ABCD можно выразить двумя способами: либо как произведение стороны ВС на высоту DAf, либо как произведение стороны АВ на высоту DH.

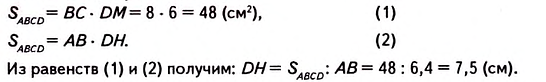
Для того чтобы найти длину неизвестной стороны или высоту параллелограмма, выразите площадь двумя способами: через одну из двух смежных сторон параллелограмма и высоту, проведённую к ней, и через другую смежную сторону и соответствующую ей высоту. Составьте и решите уравнение относительно искомой величины.

Можно ли найти площадь ромба по стороне и высоте, проведённой к ней? Можно, поскольку ромб – частный вид параллелограмма.

Вы знаете, как находить площадь прямоугольного треугольника по его катетам. Воспользуемся этим, чтобы вывести ещё одну формулу площади ромба.

Теорема (о площади ромба по его диагоналям).

Площадь ромба равна половине произведения его диагоналей.

Дано: ABCD – ромб (рис. 370), АС и BD — диагонали,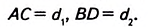

Доказать: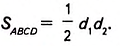

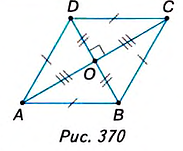
Доказательство. В ромбе ABCD все стороны равны. Его диагонали АС и BD взаимно перпендикулярны и в точке пересечения делятся пополам. Поэтому они разбивают ромб на четыре равных прямоугольных треугольника ABO, СВО, CDO и ADO с катетами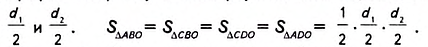

Поскольку площадь ромба равна сумме площадей этих треугольников, то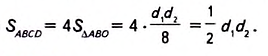

Следствие. Площадь квадрата равна половине квадрата его диагонали.

Утверждение следует из того, что квадрат – это частный вид ромба и имеет равные диагонали, пусть d. Следовательно,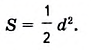

1. У вас может возникнуть вопрос: Зависит ли формула площади параллелограмма ABCD от расположения высоты DH (рис. 368)? Нет, не зависит. В расположении точки H возможны три случая. Один из них рассмотрен в учебнике. Ещё два случая: точка Н находится либо в вершине В параллелограмма (рис. 371), либо на продолжении его стороны АВ (рис. 372).

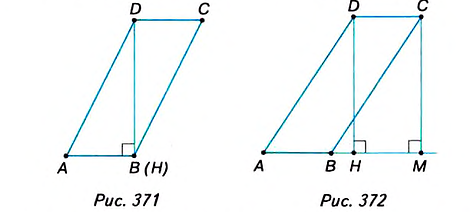
Во втором случае (рис. 371) параллелограмм ABCDсостоит из двух равных прямоугольных треугольников ABD u CDB, поэтому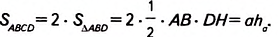

В третьем случае (рис. 372) доказательство аналогично изложенному в учебнике. Проведите это самостоятельно.

2. Для фигур, имеющих равные площади, используют специальное название — равновеликие. Например, параллелограмм ABCD и прямоугольник HMCD на рисунке 372 являются равновеликими. Понятно, что два равных многоугольника всегда равновелики, но не любые два равновеликих многоугольника равны.

Два многоугольника называются равносоставленными, если их можно разбить на одинаковое количество попарно равных многоугольников, в частности треугольников. Таковы, например, параллелограмм ABCD и прямоугольник

HMCD на рисунке 368, поскольку каждый состоит из общей для них трапеции и равных прямоугольных треугольников ADH и ВСМ.

Между равновеликими и равносоставленными фигурами существует такая связь: равносоставленные многоугольники являются равновеликими (из определения о равносоставленных многоугольниках); равновеликие многоугольники являются равносоставленными. Последнее утверждение известно, как «теорема Больяи — Гервина», доказанная в XIX в. Интересно, что Фаркаш Больяи (1775 — 1856, Венгрия), доказавший теорему, был отцом Яноша Больяи (1802 — 1860) — одного из творцов неевклидовой геометрии. Янош Больяи.

Треугольник и его площадь

Вы уже знаете, как вычислить площадь прямоугольного треугольника по его катетам. Возникает вопрос: Как найти площадь любого треугольника по его стороне и высоте, проведённой к этой стороне?

Теорема (о площади треугольника).

Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне.

Дано: 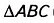(рис. 380), ‘ АН— высота, ВС= а, АН—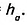

Доказать: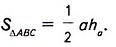

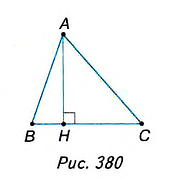
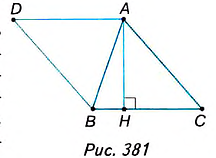
Доказательство. На стороне АВ заданного треугольника ABC построим равный ему треугольник BAD (рис. 381). Образованный четырёхугольник ADBC— параллелограмм, поскольку, по построению, AD = ВС, BD = АС. В нём сторона ВС= а, высота АН=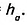, поэтому 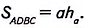. Поскольку параллелограмм состоит из двух равных треугольников ABC и BAD, то площадь треугольника ABC равна половине площади параллелограмма ADBC.

Следовательно: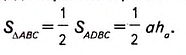

Пример №8

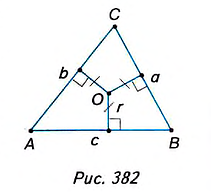
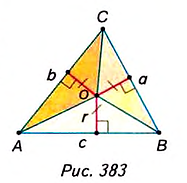
Докажите, что площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.

Решение:

Пусть ABC — данный треугольник (рис. 382), в котором ВС= а, АС— b, АВ= с, 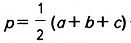— полу периметр, точка О— центр вписанной окружности, г — радиус вписанной окружности.

Докажем, что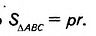

Соединим отрезками вершины треугольника ABC с центром О вписанной в него окружности (рис. 383). Получаем три треугольника — ВОС, АОС и АОВ. В каждом из них радиус вписанной окружности r является высотой, проведённой к стороне, равной соответственно a, b или с.

Поэтому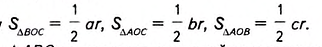 Площадь 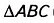равна сумме площадей этих треугольников. Следовательно, 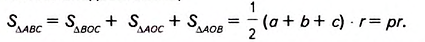Для того, чтобы найти площадь треугольника (четырехугольника) можно воспользоваться способом сложения площадей его частей. При этом иногда нужны дополнительные построения, чтобы образовались вспомогательные треугольники, площади которых можно найти по условию задачи.

1. Способы вычисления площади треугольника (а также прямоугольника и трапеции) были известны ещё в Древнем Египте. Сведения об этом дошли до нас на папирусах. Среди них наиболее известные — папирус Ринда (около 1800 г. до н. э.), содержащий 84 задачи с решениями (страница из этого папируса на рис. 384), и так называемый московский папирус (около 1600 г. до н. э.), он содержит 25 задач с решениями. Чтобы найти площадь треугольника, древние египтяне основание треугольника делили пополам и умножали на высоту. А для определения площади равнобедренного треугольника использовали полупроизведение его боковых сторон.

2. Геометрические расчёты по точным формулам проводились и в древнем Вавилоне. Сведения сохранились на клинописных табличках (образец вы видите на рис. 385). Дошедшие до нас тексты свидетельствуют, что вавилоняне знали и использовали в практических задачах пропорциональность параллельных отрезков. Например, они умели вычислять длину отрезков AW, СМ и ВМ (рис. 386) в треугольнике ABC по его стороне АС= 30, разности S, — S2 = 42 площадей трапеции и треугольника, на которые разбивается данный треугольник параллельной прямой MN, и разности ВМ — СМ = 20. Сейчас для решения этой задачи нам пришлось бы составлять систему уравнений.

Трапеция и её площадь

Вы знаете, чтобы вывести формулы площадей прямоугольника, параллелограмма или треугольника, надо составить из этих фигур такие, площади которых умеете находить. Воспользуемся этим способом и выведем формулу площади трапеции.

Теорема (о площади трапеции).

Площадь трапеции равна произведению полусуммы её оснований на высоту.

Дано: ABCD— трапеция (рис. 397),

AB и CD – основания, СН— высота, АВ=о, CD=b, CH=h. а + b

Доказать: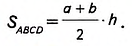

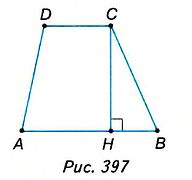
Доказательство. Проведём в трапеции диагональ АС (рис. 398). Она разбивает трапецию на два треугольника ABC и ADC. Высота h трапеции является высотой треугольника ABC, проведённой к стороне АВ = а, и равна высоте треугольника ADC, проведённой к стороне CD = b. Площадь трапеции равна сумме площадей этих треугольников, поэтому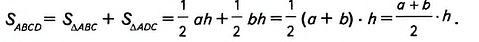

Пример №9

Диагонали АС и BD трапеции ABCD пересекаются в точке О (рис. 399). Докажите, что треугольники AOD и ВОС имеют равные площади.

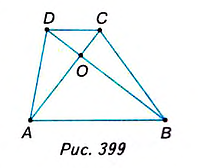
Решение:

Рассмотрим треугольники ABD и ABC. В них сторона АВ— общая, а высоты, проведённые к этой стороне, равны высоте трапеции. Поэтому 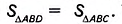Треугольник ABD состоит из треугольников АОВ и AOD, а треугольник АВС-из треугольников AOBw ВОС. Отсюда получим:

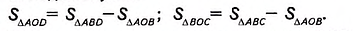
Следовательно, площади треугольников AOD и ВОС равны как разности равных площадей.

Для того чтобы установить, что неравные фигуры имеют равные площади, нужно доказать, что площади этих фигур равны либо сумме равных площадей, либо разности равных площадей.

1. У вас может возникнуть вопрос: Существует ли трапеция, средняя линия которой делит её площадь пополам?

Существование фигуры с заданными свойствами можно доказать, если привести пример такой фигуры. Однако не всегда этот путь — самый простой. История свидетельствует о том, что иногда на поиски примера, подтверждающего существование некоторого математического объекта, учёные затрачивали многие годы. Чтобы упростить поиск, проводят предварительные аналитические расчёты. Именно это мы и сделаем, чтобы ответить на поставленный вопрос. Пусть трапеция ABCD (рис. 400) имеет основания а и b и высоту h. Средняя линия MN разбивает её на две трапеции с равными высотами 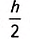(докажите этo самостоятельно). Обозначим площади этих трапеций 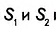и выразим их через основания данной трапеции и её высоту:

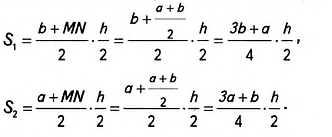
Найдём отношение площадей 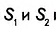После сокращений получим: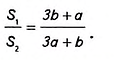

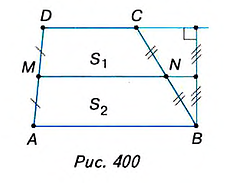
Равенство площадей 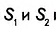возможно только в случае, если 3b + а = За + b, то есть при а= b. А такой трапеции не существует.

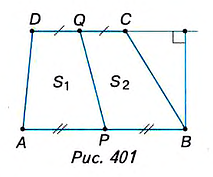
Интересно, что отрезок, соединяющий середины оснований трапеции (иногда его называют второй средней линией трапеции), делит площадь трапеции пополам. Докажите это самостоятельно, используя рисунок 401.

2. Изучая четырёхугольники, вы узнали о дельтоиде (рис. 402). Этот четырёхугольник, как и ромб, имеет взаимно перпендикулярные диагонали. Существуют трапеции со взаимно перпендикулярными диагоналями (рис. 403), а также произвольные четырёхугольники с аналогичным свойством (рис. 404). И ромб, и дельтоид, и указанная трапеция являются частными видами четырёхугольников со взаимно перпендикулярными диагоналями.

Докажите самостоятельно, что площадь четырехугольника со взаимно перпендикулярными диагоналями равна половине произведения этих диагоналей. Эта формула справедлива и для ромба, и для дельтоида, и для трапеции.

[{Large{text{Основные факты о площади}}}]

Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной (1) см, (1) мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см(^2), мм(^2) соответственно.

Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.

Свойства площади

1. Площадь любого многоугольника — величина положительная.

2. Равные многоугольники имеют равные площади.

3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

4. Площадь квадрата со стороной (a) равна (a^2).
 

[{Large{text{Площадь прямоугольника и параллелограмма}}}]

Теорема: площадь прямоугольника

Площадь прямоугольника со сторонами (a) и (b) равна (S=ab).

Доказательство

Данный квадрат состоит из прямоугольника (ABCD), еще одного равного ему прямоугольника и двух квадратов со сторонами (a) и (b). Таким образом,

(begin{multline*} S_{a+b}=2S_{text{пр-к}}+S_a+S_b Leftrightarrow
(a+b)^2=2S_{text{пр-к}}+a^2+b^2 Leftrightarrow\
a^2+2ab+b^2=2S_{text{пр-к}}+a^2+b^2 Rightarrow
S_{text{пр-к}}=ab end{multline*})

Определение

Теорема: площадь параллелограмма

Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.

Доказательство

Тогда (AB’C’D) – прямоугольник, следовательно, (S_{AB’C’D}=AB’cdot
AD).

Заметим, что прямоугольные треугольники (ABB’) и (DCC’) равны. Таким образом,

[{Large{text{Площадь треугольника}}}]

Определение

Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.

Теорема

Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.

Доказательство

Теорема

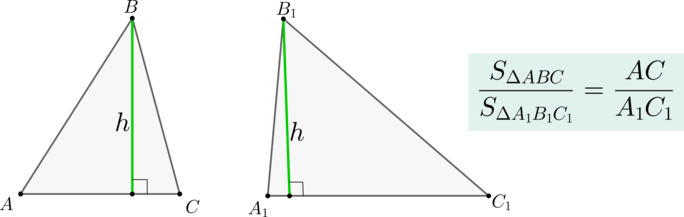
Следствие

Медиана треугольника делит его на два треугольника, равных по площади.

Теорема

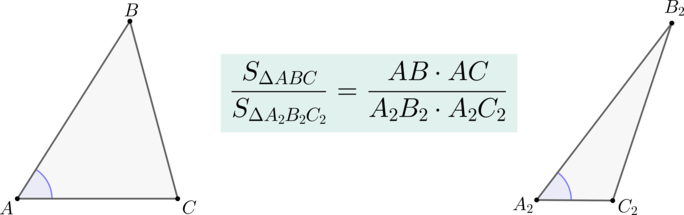
Доказательство

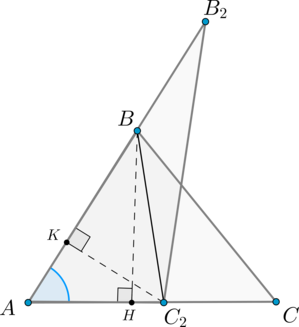
Проведем высоты (BH) и (C_2K).

Треугольники (AB_2C_2) и (ABC_2) имеют одинаковую высоту (C_2K), следовательно: [dfrac{S_{AB_2C_2}}{S_{ABC_2}}=dfrac{AB_2}{AB}]

Треугольники (ABC_2) и (ABC) имеют одинаковую высоту (BH), следовательно: [dfrac{S_{ABC_2}}{S_{ABC}}=dfrac{AC_2}{AC}]

Перемножая последние два равенства, получим: [dfrac{S_{AB_2C_2}}{S_{ABC}}=dfrac{AB_2cdot AC_2}{ABcdot AC} qquad text{ или
} qquad dfrac{S_{A_2B_2C_2}}{S_{ABC}}=dfrac{A_2B_2cdot
A_2C_2}{ABcdot AC}]

Теорема Пифагора

Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.

Теорема

Площадь прямоугольного треугольника равна половине произведения катетов.

Теорема: формула Герона

[{Large{text{Площадь ромба и трапеции}}}]

Замечание

Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.

Теорема

Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.

Доказательство

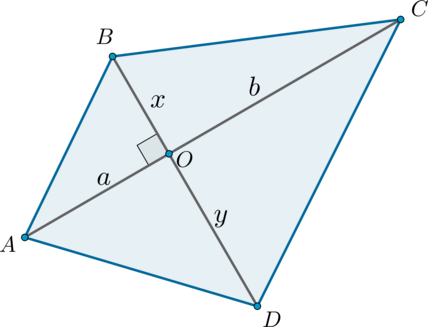
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:

(begin{multline*}
S_{ABCD}=frac12ax+frac12xb+frac12by+frac12ay=frac12(ax+xb+by+ay)=\
frac12((a+b)x+(a+b)y)=frac12(a+b)(x+y)end{multline*})

Следствие: площадь ромба

Площадь ромба равна половине произведения его диагоналей: [S_{text{ромб}}=dfrac12 d_1cdot d_2]

Определение

Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.

Теорема: площадь трапеции

Площадь трапеции равна произведению полусуммы оснований на высоту.

Доказательство

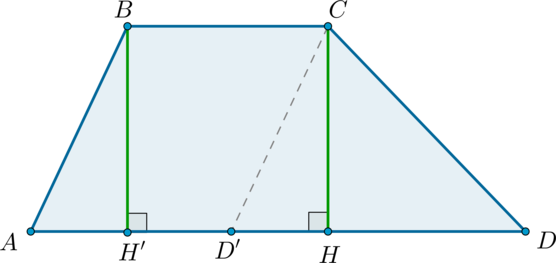
Тогда (ABCD’) – параллелограмм.

Проведем также (BH’perp AD, CHperp AD) ((BH’=CH) – высоты трапеции).

Тогда (S_{ABCD’}=BH’cdot AD’=BH’cdot BC, quad S_{CDD’}=dfrac12CHcdot D’D)

Т.к. трапеция состоит из параллелограмма (ABCD’) и треугольника (CDD’), то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:

[S_{ABCD}=S_{ABCD’}+S_{CDD’}=BH’cdot BC+dfrac12CHcdot
D’D=dfrac12CHleft(2BC+D’Dright)=] [=dfrac12
CHleft(BC+AD’+D’Dright)=dfrac12 CHleft(BC+ADright)]

Министерство образования и науки РБ

Кижингинский районный отдел образования

МБОУ «Могсохонская средняя
общеобразовательная школа

им. Дамдинжапова Ц-Д.Ж.»

Научно-практическая конференция «Шаг в
будущее»

Секция «Геометрия»

Научно-исследовательская работа

на тему:

«Вычисление площадей многоугольников
различными способами»

Выполнил: ученик 9 класса

Санданов Иван

Научный руководитель:
учитель математики Батомункуева В.С.

2019 г.

Оглавление

Введение

Основная часть

1. Теоретическая часть

1.1. Из истории возникновения понятия “Площадь”

1.2. Способы вычисления площади фигуры на клетчатой бумаге

2. Практическая часть

2.1. Три способа вычисления площади выпуклого
многоугольника

2.2. Три способа вычисления площади невыпуклого
многоугольника

2.3. Результаты эксперимента, проведенного в 9 классе

Заключение

Список литературы

Введение

В повседневной жизни мы
часто встречаемся с понятием площади. Мы говорим: площадь квартиры, площадь
садового участка и т.д. На уроках математики мы научились вычислять площади
различных многоугольников, мы знаем формулы для вычисления площади квадратов,
прямоугольников, параллелограммов, ромбов, трапеций, треугольников.

Так как на уроке мы
обычно выполняем решение в тетради, то я обратил внимание, что вычислить
площадь многоугольников помогают клетки, изображенные в тетради. Просматривая
различную информацию в интернете,  я натолкнулся на формулу, которая позволяет
вычислить площадь фигуры, изображённой на клетчатой бумаге по её узлам.
Впоследствии мне захотелось изучить различные способы для вычисления площадей
многоугольников на клетчатой бумаге и сравнить их.

Гипотеза: формула Пика удобна и менее затратна по времени для вычисления
площади геометрической фигуры, изображенной на клетчатой бумаге.

Актуальность выбранной
темы: использование различных
способов вычисления площади фигур на клетчатой бумаге усиливает интерес
учащихся к математике и содействует развитию математических способностей
школьников.

Цель
работы: исследовать различные
способы вычисления площадей фигур на клетчатой бумаге, сравнить полученные
результаты.

Задачи
исследования:

1.    изучить  теоретический материал по исследуемой теме;

2.    вычислить площади различных многоугольников на клетчатой бумаге
различными способами и сравнить их;

3.    провести эксперимент в 9 классе, показывающий каким из
предложенных способов учащиеся лучше вычисляют площадь многоугольников, какой
способ им больше нравится;

4.    проанализировать и систематизировать полученную информацию.

Объект
исследования: задачи  на вычисление
площади различных фигур на клетчатой бумаге.

Предмет
исследования: способы вычисления площади фигур
на клетчатой бумаге.

Методы
и исследования:  моделирование,
сравнение, обобщение, аналогии, анализ и классификация информации.

Практическая
значимость исследования: результаты
исследования могут быть использованы на уроках геометрии, в жизни при
вычислении различных площадей (здания, участка земли т.д.), а также при
подготовке к ОГЭ.

Основная
часть

1. Теоретическая
часть

1.1.
Из истории возникновения понятия “Площадь”

Измерение площадей
является одним из самых древних разделов геометрии. В частности, название
“геометрия” означает “землемерие”, т.е. связано именно с измерением площадей.
Основы этой науки были заложены в Древнем Египте, где после каждого разлива
Нила приходилось заново производить разметку участков, покрытых плодоносным
илом, т. е. вычислять их площади.

Вавилоняне, так же как и египтяне
измеряли большей частью простейшие фигуры, встречающиеся при межевании земель, возведении
стен и насыпей, строительстве плотин и каналов и т.п.

Сохранилось немало планов
земельных угодий, разделенных на прямоугольники, трапеции и треугольники, а также
планов различных строений, свидетельствующих, что вавилонский землемер или архитектор
должен был хорошо чертить и проводить геометрические расчеты.

Многие ученые решали
проблему вычисления площади фигуры. В историю с понятием площади вошли имена
Евклида, Архимеда, Пифагора, Герона Александрийского, Рене Декарта, Пьера
Ферма, Георга Пика и др. Ими открыто большое количество различных формул и
способов для вычисления площади фигуры.

1.2.
Способы вычисления площади фигуры на клетчатой бумаге

При изучении вычисления
площадей многоугольников на клетчатой бумаге я заметил, что все задачи строятся
на понятии узла. Узел напоминает узел в рыболовной сетке – пересечение
горизонтальных и вертикальных линий.

Рисунок 1 – Рыболовная сеть

Рассмотрим
вычисление площади одной и той же фигуры тремя способами  и сравним результат
вычисления.

2. Практическая
часть

2.1. Три способа вычисления площади выпуклого
многоугольника

Разбиение. Смысл данного способа состоит в том, что многоугольник разрезается
на прямоугольники и (или) прямоугольные треугольники с вершинами в узлах сетки.

Рисунок 2 –
вычисление площади выпуклого многоугольника методом разбиения

Тогда площадь фигуры
можно сосчитать по формуле:

S_ф
= S₁
+ S₂
+ S₃
+ S₄=
4 + 1,5 + 1+1 = 7,5.

Рисунок 3 – Вычисление площади
выпуклого  многоугольника методом дополнения до прямоугольника

Дополнение до
прямоугольника. Смысл данного способа –
это дополнение многоугольника до прямоугольника так, чтобы его стороны проходили через вершины четырехугольника, а затем вычитание лишних частей. Получим, что площадь фигуры
равна:

S_ф
= S_пр
 – (S₁ + S₂+S₃) = 12 – (1,5 + 1+2) =
7,5.

Формула Пика. Любая фигура изображенная
на листе бумаги делит его на внутреннюю область  и внешнюю, а еще есть
граничные точки многоугольника. Нас интересуют внутренние узлы и узлы, которые
лежат на границе многоугольника. Тогда формула выглядит так  

где В – количество внутренних узлов;

Г – количество узлов на границе
многоугольника.    

Эта формула получила название формула Пика
в честь австрийского математика Георга Пика которая появилась в его
восьмистраничной работе 1899 года, опубликованной в Праге.

Используя рисунок  В= 5, Г = 7, получаем

Вычисляя
площадь выпуклого многоугольника тремя способами, я получил один и тот же
результат.                                                                                                        

2.2. Три способа вычисления площади невыпуклого
многоугольника

Далее я вычислил площадь
невыпуклого многоугольника этими тремя способами.

Рисунок 5 –
Вычисление площади невыпуклого многоугольника методом разбиения

По способу разбиения
площадь фигуры можно сосчитать по формуле:

S_ф
= S₁
+ S₂=
2+2=4

Рисунок 6 –
Вычисление площади невыпуклого многоугольника методом дополнения до
прямоугольника

Достраивая многоугольник до
прямоугольника, и отсекая лишние части,  найдем площадь фигуры

S_ф = S – (S₁ + S₂
+ S₃) = 12 – (2 + 3 + 3) = 12 – 8 = 4.

Рисунок 7 – Вычисление площади
невыпуклого многоугольника по формуле Пика

При подсчете внутренних узлов
многоугольника и узлов, лежащих на границе получим, что

В = 3; Г = 4;
S = 3 + 4/2 – 1 = 4.

И опять я получил один и
тот же результат.

Сравнив результаты я
сделал вывод, что вычисление площади по формуле Пика более удобно и менее
затратно по времени.

 

2.3.
Результаты эксперимента, проведенного в 9 классе

Сделав сравнительный анализ, я провел
эксперимент в  своем  классе с целью развития познавательной активности на
уроках геометрии и выявления математических знаний у учащихся при вычислении
площади фигур. Мной был проведен элемент урока в 9 классе. Я предложил своим
одноклассникам вычислить площадь многоугольника двумя способами: по формуле
площадей многоугольников и по формуле Пика (Приложение 2).

Ребята с интересом отнеслись к моему
заданию, но не у всех получились одинаковые результаты. Хотя формула Пика и
легка при вычислении площади, у многих сложность возникла при нахождении узлов
на границе фигуры и внутри нее.

Заключение

Изучив различные источники, выяснилось, что существует различные способы
вычисления фигур по клеткам, но для меня были интересны и понятны три:
разбиение, дополнение до прямоугольника  и
вычисления по формуле Пика.

Моя гипотеза
– о том, что если геометрическая фигура
изображена на клетчатой бумаге, то ее площадь можно вычислить различными
способами и убедиться, что результаты вычислений будут одинаковыми,  подтвердилась. Рассмотрев все три способа, я пришел к выводу, что формула Пика
интересна своей простотой. Формулу Пика изучают по школьной программе во многих
странах Европы.

Проведя эксперимент в 9  классе я обратил внимание, что вычислять
площадь многоугольников по клеткам  ребятам интересно, но не хватает практики,
одного занятия недостаточно. Нужно закреплять навык вычисления площадей.

 Задачи на клетчатой бумаге встречаются в заданиях ОГЭ, поэтому я считаю, что такие задания нужно включать в элемент урока, так как
это  поможет им при подготовке к экзаменам.

Список литературы

1.                 
Атанасян Л. С. Геометрия 7-9, учебник. –
М.Просвещение,2009.

2.                 
Жарковская Н. М., Рисс Е. А. Геометрия
клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25.

3.                 
 История математики с
древнейших времен до начала XIX столетия, под редакцией Ю.П. Юшкевича.,
издательство Наука., М., 1970г

4.
Смирнова И. М., Смирнов В. А. Геометрия на клетчатой бумаге. – М.: Чистые
пруды, 2009.

Интернет
ресурсы:

http://www.pppa.ru/additional/01geodesy/06/02topo.php

http://ru.wikihow.com http://knowledge.allbest.ru/mathematics/3c0b65635b3bd68b4c43b89521306d27_0.html

http://argonavt.narod.ru/Kenpark.html

http://infourok.ru/issledovatelskaya-rabota-vichislenie-ploschadi-mnogougolnika-na-kletchatoy-bumage-910671.html

https://docviewer.yandex.ru

Приложение 1.

В 6 из 10 заданий учащиеся лучше справились по формуле Пика,

В 1 задании результаты оказались одинаковыми.

80 % учащихся ответили, что им больше понравилось вычислять
площадь по формуле Пика.

Всего: 10 учащихся