Как найти площадь выпуклого шестиугольника

Шестиугольник — многоугольник, у которого есть шесть сторон и шесть углов. В правильном заданном
многоугольном геометрическом объекте все стороны равняются друг другу, а углы формируют шесть
равносторонних треугольников.

Площадь правильной фигуры с шестью углами — положительная величина некоторой области плоскости,
занимаемой данным многоугольным геометрическим объектом.

Выделяют ряд методов нахождения площади этого многоугольника, зависимо от его типа.

Через длину стороны

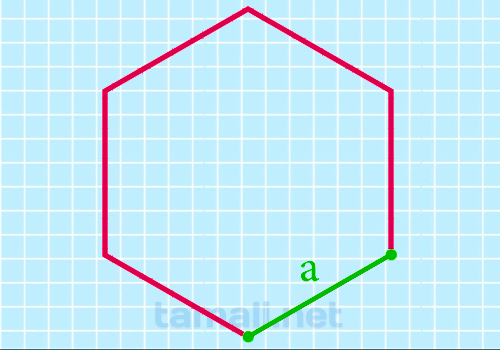
По той причине, что выпуклый шестиугольник включает в себя шесть равносторонних треугольников, тогда
формула нахождения требуемой величины через длину стороны выглядит следующим образом:

S = (3√3*a²)/2

где a — это продолжительность стороны.

Рассмотрим пример. Пусть длина стороны эквивалентна 8. Тогда, согласно этой формуле, заданную
характеристику замкнутого выпуклого шестиугольника будет примерно равна 166.

Всё достаточно
просто, если сторона заранее известна. Если же эта величина нам не дана, но известен периметр или
апофема — высота одного из шести равносторонних треугольников — тогда длину стороны можно
высчитать.

В случае, если известен периметр, его необходимо поделить на шесть, таким образом получается длина
стороны. К примеру, если периметр равен 36, то, поделив 36 на 6, получается 6 — это и есть
протяжённость стороны.

Если известна лишь апофема, тогда можно посчитать длину стороны, подставив апофему в формулу b = x√3 и умножив ответ на 2. Всё это потому, что апофема — это сторона
x√3 составляемого ей треугольника с углами 30, 60 и 90 градусов. К примеру, если апофема 11√3, то
x = 11, а протяжённость стороны будет эквивалентна 22.

Через периметр

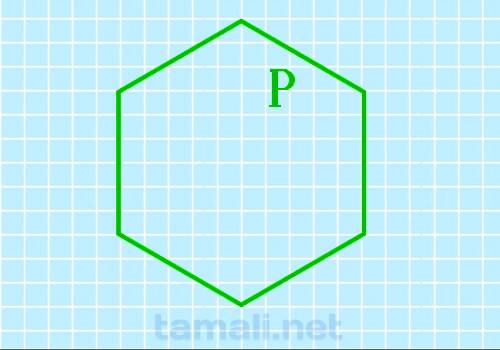
Если при изучении правильной фигуры с шестью углами нам известен только его периметр, несложно
рассчитать площадь этой фигуры по такой формуле:

S = (3√3*(p/6)²)/2

где p — это периметр фигуры.

Допустим, если периметр будет равняться 24, тогда площадь будет примерно эквивалентна 42. Если в
качестве периметра возьмём число 50, тогда площадь фигуры окажется 180.

Через длинную диагональ

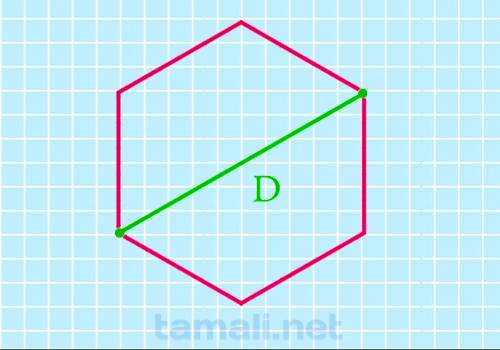
Длинная или большая диагональ шестиугольника — это диаметр описанной вокруг него плоской кривой, как
правило, она равняется двум его сторонам.

Используем такое выражение для подсчёта площади подобного правильного многоугольного геометрического
объекта через длинную диагональ этого множества точек:

S = (3√3*D²)/8

где D — это длинный отрезок, соединяющий несмежные вершины.

К примеру, если D = 6, тогда заданная характеристика замкнутого выпуклого
многоугольника будет приблизительно равна 23. Если в качестве длинной диагонали возьмём 8, тогда
величина будет примерно эквивалентна 42.

Через короткую диагональ

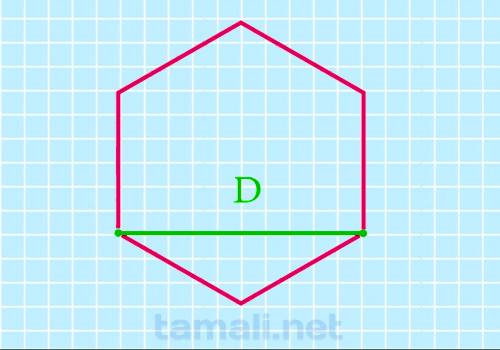
Меньшая или короткая диагональ правильного шестиугольника в √3 раз длиннее его стороны, также она
образует с ней прямой угол.

Если известна короткая диагональ такого выпуклого многоугольника, то с её помощью можно найти площадь
этой фигуры следующим образом:

S = (√3*D²)/2

где D — это протяжённость короткого отрезка, соединяющего несмежные
вершины.

К примеру, если длина такой диагонали будет равна 14, тогда необходимая характеристика фигуры будет
примерно равняться 170. Если же в качестве D мы возьмём 2, тогда величина
окажется всего лишь 3.

Через радиус описанной окружности

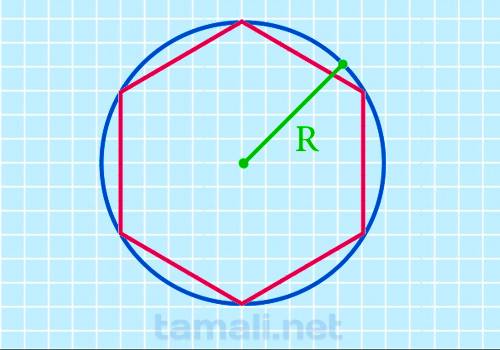
Шестиугольник считается правильным многоугольником, ведь все его стороны и углы эквивалентны друг
другу. Соответственно, около такого многоугольника можно описать окружность.

Чтобы найти площадь выпуклого многоугольника через радиус описанной окружности, необходимо
воспользоваться такой формулой:

S = (3√3*R²)/2

где R — это отрезок, соединяющий центр и любую точку описанной замкнутой
плоской кривой.

К примеру, если отрезок, соединяющий центр и любую точку, равняется 5, тогда заданная характеристика
замкнутой фигуры будет примерно равна 65. Если же в качестве радиуса возьмём число 12,
соответственно, заданная характеристика замкнутой фигуры получится примерно 374.

Через радиус вписанной окружности

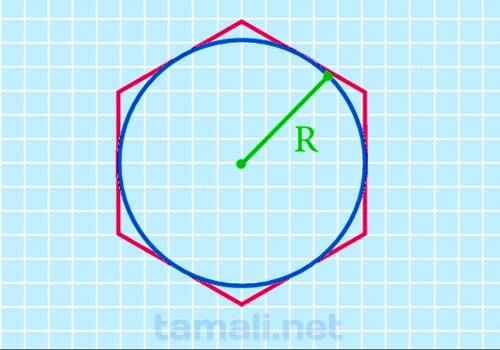
Шестиугольник считается правильным многоугольником, ведь все его стороны и углы равны друг другу.
Соответственно, во всякий шестиугольник можно вписать окружность.

Формула для расчёта площади следующего выпуклой фигуры с шестью углами через радиус вписанной
окружности будет выглядеть следующим образом:

S = √3*r²

где r — это отрезок, соединяющий центр и любую точку вписанной замкнутой
плоской кривой.

К примеру, если этот отрезок, соединяющий центр и любую точку, равен 14, тогда необходимая величина
этого множества точек будет примерно равна 679. Если в качестве отрезка, соединяющего центр и любую
точку, возьмем 4, тогда площадь будет приблизительно равна 55.

Что такое правильный шестиугольник

Этот многоугольный геометрический объект имеет определённые свойства:

• Каждый угол этой фигуры равняется 120 градусам;
• Вокруг правильного шестиугольника можно описать окружность, причем единственную, а её радиус
  равняется его стороне;
• Большие диагонали такого выпуклого многоугольника разделяют его на шесть равносторонних
  треугольников, высота каждого равняется радиусу вписанной в выпуклый многоугольник окружности;
• Центры вписанной и описанной окружностей около подобного выпуклого многоугольника — это точка
  пересечения больших диагоналей этого множества точек.

Эта фигура очень часто встречается в природе, технике и культуре. К примеру:

• Пчелиные соты изображают разделение плоскости на выпуклые шестиугольники;
• Некоторые сложные молекулы углерода имеют гексагональную кристаллическую решётку;
• Сечение гайки и большинства карандашей описывается таким выпуклым многоугольником;
• Гексаграмма — это шестиконечная звезда, сформированная двумя правильными треугольниками. Также
  её называют звездой Давида, она считается символом иудаизма.

Как найти площадь шестиугольника

Шестиугольник – это многоугольник, имеющий 6 сторон и 6 углов. В зависимости от того, правильный шестиугольник или нет, существует несколько методов нахождения его площади. Мы рассмотрим все.

1

Как найти площадь правильного шестиугольника

Формулы для вычисления площади правильного шестиугольника – выпуклого многоугольника с шестью одинаковыми сторонами.

Дана длина стороны:

• Формула площади: S = (3√3*a²)/2
• Если длина стороны a известна, то подставив её в формулу, мы легко найдём площадь фигуры.
• В противном случае длину стороны можно найти через периметр и апофему.
• Если задан периметр, то мы просто делим его на 6 и получаем длину одной стороны. Например, если периметр равен 24, то длина стороны будет равняться 24/6 = 4.
• Апофема – перпендикуляр, проведённый из центра к одной из сторон. Чтобы найти длину одной стороны, подставляем длину апофемы в формулу а = 2*m/√3. То есть, если апофема m = 2√3, то длина стороны а = 2*2√3/√3 = 4.

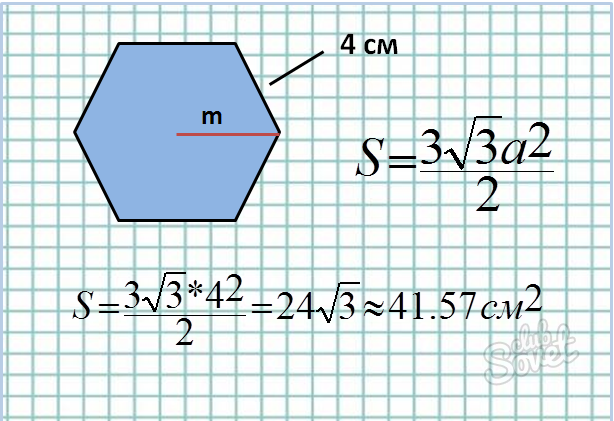
Дана апофема:

• Формула площади: S = 1/2*p*m, где p – периметр, m – апофема.
• Найдём через апофему периметр шестиугольника. В предыдущем пункте мы научились находить длину одной стороны через апофему: а = 2*m/√3. Осталось только этот результат умножить на 6. Получаем формулу периметра: p = 12*m/√3.

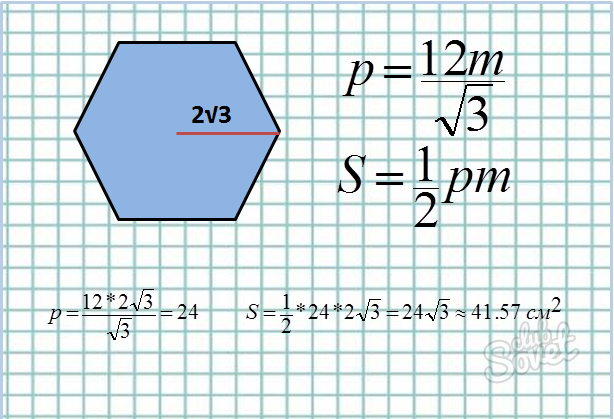
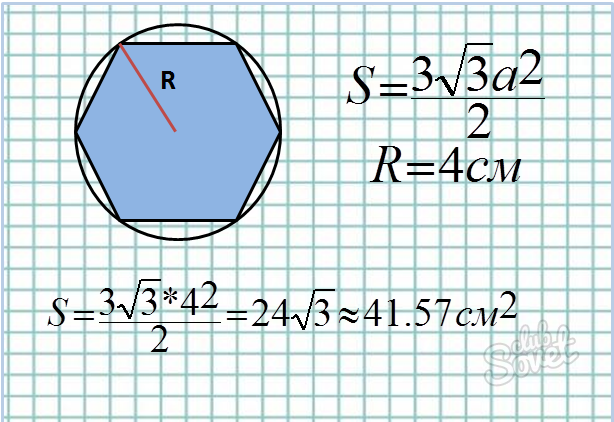
Дан радиус описанной окружности:

• Радиус описанной вокруг правильного шестиугольника окружности равен стороне этого шестиугольника.
  Формула площади: S = (3√3*a²)/2

Дан радиус вписанной окружности:

• Формула площади: S = 3√3*r², где r = √3*a/2 (a – одна из сторон многоугольника).

2

 Как найти площадь неправильного шестиугольника

Формулы для вычисления площади неправильного шестиугольника – многоугольника, стороны которого не равны между собой.

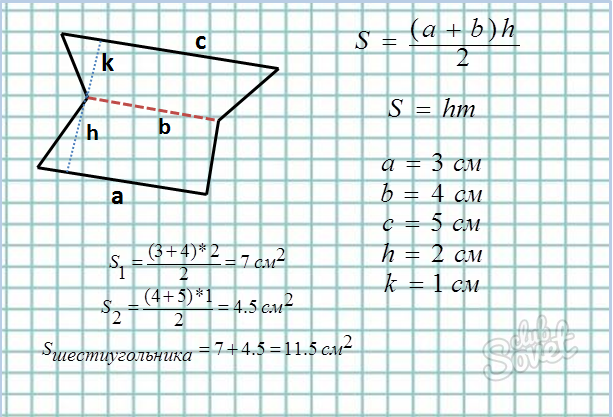
Метод трапеции:

• Делим шестиугольник на произвольные трапеции, вычисляем площадь каждой из них и складываем.
• Основные формулы площади трапеции: S = 1/2*(a + b)*h, где a и b – основания трапеции, h – высота.
  S = h*m, где h – высота, m – средняя линия.

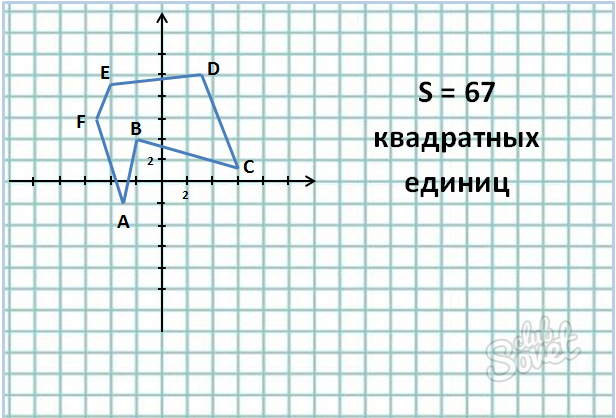
Известны координаты вершин шестиугольника:

• Для начала запишем координаты точек, причём, располагая их не в хаотичном порядке, а последовательно друг за другом. Например:
  A: (-3, -2)
  B: (-1, 4)
  C: (6, 1)
  D: (3, 10)
  E: (-4, 9)
  F: (-5, 6)
• Далее, внимательно, умножаем координату x каждой точки на координату y следующей точки:
  -3*4 = -12
  -1*1 = -1
  6*10 = 60
  3*9 = 27
  -4*6 = -24
  -5*(-2) = 10
  Результаты складываем:
  -12 – 1 + 60 + 27 – 24 + 10 = 60
  Далее умножаем координату y каждой точки на координату x следующей точки.
  -2*(-1) = 2
  4*6 = 24
  1*3 = 3
  10*(-4) = -40
  9*(-5) = -45
  6*(-3) = -18
  Результаты складываем:
  2 + 24 + 3 – 40 – 45 – 18 = -74
  Из первого результата вычитаем второй:
  60 -(-74) = 60 + 74 = 134
  Полученное число делим на два:
  134/2 = 67
  Ответ: 67 квадратных единиц.

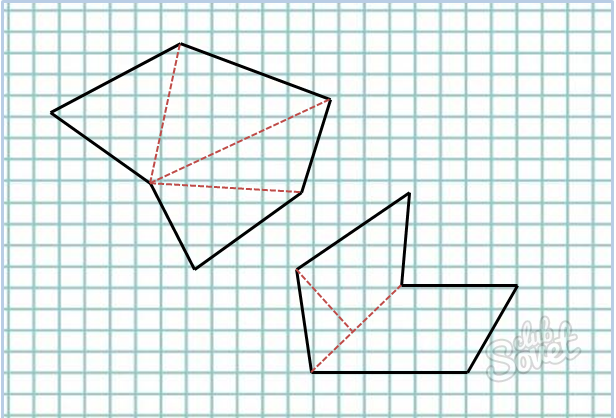
• Также для нахождения площади шестиугольника вы можете разбить его на треугольники, квадраты, прямоугольники, параллелограммы и так далее. Найти площади составляющих его фигур и сложить.

Итак, методы нахождения площади шестиугольника на все случаи жизни изучены. Теперь вперёд, применять полученные знания! Удачи!

От теории к практике

Свойства шестиугольника очень активно используются как в природе, так и в различных областях деятельности человека. В первую очередь это касается болтов и гаек — шляпки первых и вторые представляют собой ничто иное, как правильный шестигранник, если не брать в расчет фаски. Размер гаечных ключей соответствует диаметру вписанной окружности — то есть расстоянию между противоположными гранями.

Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:

Выпускается и бетонная плитка для мощения.

https://youtube.com/watch?v=dXAWHtYgFyQ

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

180°(n-2),

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:

1. чертится прямая линия и на ней ставится точка;
2. из этой точки строится окружность (она является ее центром);
3. из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
4. после этого отрезками последовательно соединяются все точки на первой окружности.

При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

1. диаметр описанной окружности;
2. диаметр вписанной окружности;
3. площадь;
4. периметр.

Описанная окружность и возможность построения

Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

S=3(2r/√3)²(√3)/2=r²(2√3)

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

1. Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
2. Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
3. Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

1. Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
2. Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
3. Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
4. Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

r₂=а/2

Площадь нового шестиугольника можно посчитать так:

S=(3(√3)/2)(а(√3)/3)²=а(√3)/2

Площадь неправильного шестиугольника

Существует несколько вариантов определения площади
неправильного шестиугольника:

• Метод трапеции.
• Метод расчета площади неправильных многоугольников при
  помощи оси координат.
• Метод разбивания шестиугольника на другие фигуры.

В зависимости от исходных данных, которые вам будут
известны, подбирается подходящий метод.

Метод трапеции

Площадь шестиугольника, имеющего произвольную
(неправильную) форму, рассчитывается методом трапеции, суть которого состоит в
разделении шестиугольника на отдельные трапеции и последующим вычислением
площади каждой из них.

Метод с осями
координат

Кроме этого, площадь неправильного шестиугольника можно рассчитать
при помощи метода расчета площади неправильных многоугольников. Рассмотрим его
на следующем примере:

Вычисление будем выполнять методом использования
координат вершин многоугольника:

1. На этом этапе следует сделать таблицу и записать
   координаты вершин x и y. Выбираем вершины в
   последовательном порядке по направлению против часовой стрелки, завершив конец
   списка повторной записью координаты первой вершины:

1. Теперь следует умножить значения координаты х 1-й вершины
   на y 2-й
   вершины и продолжить таким образом умножение далее. Затем необходимо сложить
   полученные результаты. В нашем случае получилось 82:

1. Последовательно умножаем значения координат y1-й
   вершины на значения координат х 2-й вершины. Суммируем полученные результаты. В
   нашем случае получилось 38:

1. Вычитаем сумму, которую получили на четвертом этапе из
   суммы, которая получилась на третьем этапе: 82 – (-38) = 120

1. Теперь необходимо разделить результат, который был
   получен на предыдущем этапе и найдем площадь нашей фигуры: S= 120/2 = 60
   см²

Метод разбивания
шестиугольника на другие фигуры

Каждый многоугольник можно разделить на несколько других
фигур. Это могут быть треугольники, трапеции, прямоугольники. Исходя из
известных данных, пользуясь формулами определения площадей перечисленных фигур,
последовательно вычисляются их площади и затем суммируются.

Некоторые неправильные шестиугольники состоят из двух
параллелограммов. Для определения площади параллелограмма следует умножить его
длину на ширину и затем сложить две уже известные площади.

Видео о том, как найти площадь многоугольника

https://youtube.com/watch?v=N8kcd6smUy4

Площадь равностороннего шестиугольника

Равносторонний шестиугольник имеет шесть равных сторон и
является правильным шестиугольником.

Площадь равностороннего шестиугольника равняется 6
площадям треугольников, на которые разбита правильная шестиугольная фигура.

Все треугольники в шестиугольнике правильной формы равны,
поэтому для нахождения площади такого шестиугольника достаточно будет знать
площадь хотя бы одного треугольника.

Для нахождения площади равностороннего шестиугольника
используется, конечно же, формула площади правильного шестиугольника, описанная
выше.

А Вы знали, как найти площадь шестиугольника? Как думаете, где эти знания пригодятся Вам в жизни? Поделитесь своим мнением в .

Шестиугольник, выпуклый и невыпуклый шестиугольник:

Шестиугольник – это многоугольник с шестью углами.

Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.

Шестиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый шестиугольник

  Рис. 2. Невыпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

.

Чем он отличается от неправильного?

Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.

В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.

В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.

Похожее

• Пчелиные соты становятся шестиугольными без помощи пчёл

  Регулярный ячеистый рисунок можно сделать, если ячейки будут треугольными, квадратными или шестиугольными. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска. Впервые такую «экономность» пчёл заметили в IV веке н. э., и тогда же было высказано предположение, что пчёлы при постройке сотов «руководствуются математическим планом». Однако, полагают исследователи из Кардиффского университета, инженерная слава пчёл сильно преувеличена: правильная геометрическая форма шестигранных ячеек сотов возникает из-за, действующих на них физических сил, а насекомые тут лишь помощники.
• Почему стекло прозрачное?
  Марк Медовник

• Рождённые из кристаллов?
  Николай Юшкин
  По своей структуре простейшие биосистемы и углеводородные кристаллы необыкновенно похожи. Если такой минерал дополнить компонентами белка, то мы получим реальный протоорганизм. Именно так видит начало начал кристаллизационная концепция происхождения жизни.

• Споры о структуре воды
  Маленков Г. Г.
  Споры о структуре воды вот уже не одно десятилетие волнуют как научную общественность, так и людей, с наукой не связанных. Этот интерес не случаен: структуре воды порой приписывают целебные свойства, причём многие уверены, что этой структурой можно управлять каким-то физическим методом либо просто силой духа. А каково мнение учёных, которые не одно десятилетие занимаются изучением тайн воды в жидком и твёрдом состоянии?

• Мед и медолечение
  Стоймир Младенов

  Используя опыт других исследователей и результаты собственных экспериментальных и клиническо-экспериментальных исследований, автор в пределах своих возможностей указывает на лечебные свойства пчелиного меда и на методы его применения в медицине. Желая придать этому труду более законченный вид, и чтобы читатель получил более целостное представление о хозяйственном и медицинском значении пчел, в книге кратко будут рассмотрены и другие продукты пчеловодства, неразрывно связанные с жизнью пчел, а именно: пчелиный яд, пчелиное маточное молочко, цветочная пыльца, воск и прополис, а также и отношение науки к этим продуктам.

• Каустики на плоскости и в пространстве

  Каустики — это вездесущие оптические поверхности и кривые, возникающие при отражении и преломлении света. Каустики можно описать как линии или поверхности, вдоль которых концентрируются световые лучи.

• Как работает транзистор?
  Они повсюду: в каждом электроприборе, начиная с телевизора и заканчивая старыми тамагочами. Мы не знаем о них практически ничего, ведь воспринимаем их как данность. Но без них мир бы полностью изменился. Полупроводники. О том, что это такое и как они работают.

• Полет шмеля оказался устойчив к турбулентности

  Международный коллектив ученых выяснил, насколько легко приходится шмелям летать в сильно ветреную погоду. Оказалось, что даже в условиях значительной турбулентности особый механизм создания подъемной силы позволяет насекомым оставаться на лету с минимальными дополнительными затратами энергии.

• Открыт механизм самоорганизации нанокристаллов карбонатов и силикатов в биоморфные структуры
  Елена Наймарк

  Испанские ученые открыли механизм, который может приводить к спонтанному образованию кристаллов карбонатов и силикатов очень сложной и необычной формы. Эти кристаллические новообразования напоминают биоморфы — неорганические структуры, полученные при участии живых организмов. А механизм, приводящий к такой мимикрии, на удивление прост — это всего лишь самопроизвольные колебания pH раствора карбонатов и силикатов на границе формирующегося твердого кристалла и жидкой среды.

• Ледяные узоры высокого давления
  Комаров С. М.

Далее >>>

Определение

Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.

Замечание

Т.к. сумма всех углов (n)–угольника равна (180^circ(n-2)), то каждый угол правильного (n)–угольника равен [alpha_n=dfrac{n-2}n cdot 180^circ]

Пример

Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac {4-2}4cdot 180^circ=90^circ);

каждый угол правильного шестиугольника равен (dfrac{6-2}6cdot
180^circ=120^circ).

Теоремы

1. Около любого правильного многоугольника можно описать окружность, и притом только одну.

2. В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствия

1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.

2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.

Теорема

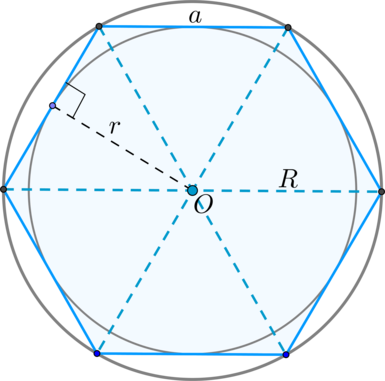
Свойства правильного шестиугольника

1. Сторона равна радиусу описанной окружности: (a=R).

2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.

3. Все углы правильного шестиугольника равны (120^circ).

4. Площадь правильного шестиугольника со стороной (a) равна (dfrac{3sqrt{3}}{2}a^2).

5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.

6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).

Замечание

В общем случае правильный (n)-угольник инвариантен относительно поворота на угол (dfrac{360^circ}{n}).

A hexagon is a closed two-dimension geometrical shape. It has six sides of the same or different lengths, six vertices, and six interior angles. In the regular hexagon, all the interior angles are of 120° and exterior angles are of 60°. A regular hexagon has 9 diagonals and can be split into six equilateral triangles. Hexagon is of four types:

• Regular Hexagon: The hexagon having all sides of equal length and with an interior angle 120° is known as a regular hexagon. The diagonals of regular hexagons are equal. They intersect at the center of the hexagon. 
• Irregular Hexagon: The hexagon with unequal sides is said to be an irregular hexagon. In an irregular hexagon, all the internal angles are not equal to 120° but their sum is equal to 720°.
• Convex Hexagon: The hexagon having all the vertices pointed outward is known as a convex hexagon. It can be a regular or irregular hexagon and the interior angles are less than 180°.
• Concave Hexagon: The hexagon in which at least one vertex points inward is known as the Concave Hexagon. In this, at least one interior angle is greater than 180°.

Area of a Hexagon

As we know the hexagon is a geometrical shape and has six sides and vertices. So the area of a hexagon(regular hexagon) is 

Area of Hexagon =  3√3/2 x²

Here, x is known as the length of its sides. Here we use a regular hexagon so the length of all the sides is equal.

Derivation for the formula:

As we know a hexagon contains six triangles with a center point as a common vertex. Its area can be found by considering the six times the area of an equilateral triangle.

So the area of hexagon = 6 * Area of triangle

As we know the area of triangle  =  1/2 * base * height

where, the base is going to be the one of the side of triangle i.e., a (let)

Now we calculate height using pythagoras theorem

From the above fig. the vertical line drawn from one of the vertex to the center of base gives the height.

height² = a² – (a/2)² (from pythagoras theorem)

             = √3a²/2

Area of triangle  = 1/2 * a * √3a/2

                            = √3a²/4

Area of hexagon = 6 * Area of  triangle

                             = 6 * √3/4 * x²

                             = 3√3/2 * x²

One can consider, the area of triangle =  1/2 *  a *  b * sin ∅ , 

where a is the side of the triangle, b is the side of the triangle and ∅ included angle between the two sides a and b

In equilateral triangle, a = b = x (let) and ∅ = 60° 

So the area of equilateral triangle = 1/2 *  x *  x * sin 60°

                                                         = 1/2*  x ² * √3/2 [ sin 60° = √3/2 ]

                                                         = √3/4 * x²

Hence the area of hexagon = 6 * Area of Equilateral triangle

                                              = 6 * √3/4 * x²

                                              = 3√3/2 * x²

There isn’t a peculiar method to calculate the area of a regular hexagon. It is calculated by breaking down the regular hexagon into triangles and quadrilaterals and summing up their individual areas at last.

Area of the hexagon with apothem

We can also calculate the area of a hexagon with apothem. Apothem is a line segment that is drawn from the center and perpendicular to the sides of the hexagon. So the area is 

Area of Hexagon = 1/2 x perimeter(hexagon) x apothem

Or we can say

Area of hexagon = 1/2  x 6y x a = 3ya

Here, a is known as apothem and y is known as the length of the sides 

Sample Question

Question 1. Find the area of a hexagon whose side length is 3cm.

Solution:

Given the side of hexagon as 3cm i.e., a = 3cm

Area of hexagon  = 3√3/2 a²

                                      = 3√3/2 (3 * 3)

                             = 27 √3/2 cm²

Question 2. Find the area of the hexagon with a side length of 2√3 cm.

Solution:

Given the side of hexagon as 3cm i.e., a = 3cm

Area of hexagon  = 3√3/2 a²

                             = 3√3/2(2√3 * 2√3)

                             = 18√3 cm²

Question 3. Find the area of a hexagon whose side length is 6cm.

Solution:

Given the side of hexagon as 3cm i.e., a = 6cm

Area of hexagon  = 3√3/2 a²

                             = 3√3/2(6 * 6)

                             = 54 √3 cm²

Question 4. Find the area of the hexagon with a side length of 2√6 cm.

Solution:

Given the side of hexagon as 3cm i.e., a = 2√6cm

Area of hexagon  = 3√3/2 a²

                            = 3√3/2(2√6 * 2√6)

                            = 36√3 cm²

Last Updated :
29 Jan, 2022

Like Article

Save Article