Как найти площадь заданной четырьмя уравнениями

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми и и графиком функции . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция неотрицательна на отрезке и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

где — площадь внутренней ступенчатой фигуры, —площадь внешней ступенчатой фигуры, и . С другой стороны, по определению интеграла можно записать:

Таким образом, числа и разделяют одни и те же числовые множества: . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции , сверху графиком функции , а слева и справа прямыми (рис. 30), то ее площадь выражается формулой

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами .

Пусть теперь функция непрерывна на отрезке и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке функции , которая на принимает только неотрицательные значения. По доказанному выше

Как мы видим, в рассматриваемом случае интеграл дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке в конечном числе точек, то значение интеграла дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой , осью абсцисс и прямыми (рис. 33).

Решение. Имеем: (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы и отрезком прямой (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

Пример 3. Найти площадь фигуры, ограниченной графиками функций (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника и прямоугольного треугольника

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Записав уравнение кривой в виде , найдем точки пересечения ее с осью , положив . Учитывая сказанное, найдем площадь половины петли:

Воспользовавшись формулой из таблицы при , получим:

Значит, окончательно имеем:

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая задана в параметрической форме

где функция монотонна на отрезке , причем , и имеет на этом отрезке непрерывную производную. Так как , то по формуле замены переменной под знаком определенного интеграла получаем:

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

Пример 5. Вычислить площадь эллипса, заданного параметрически

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке соответствует значение , а точке — значение . Поэтому

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами и , выходящими из точки , и непрерывной кривой (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть — полярное уравнение кривой , а и — углы между полярной осью и лучами и соответственно. При этом пусть функция непрерывна на .

Разобьем данный сектор на частей лучами

и рассмотрим k-й частичный сектор (рис. 39). Пусть — наименьшее значение функции в , a — наибольшее значение функции в этом отрезке.

Построим два круговых сектора с радиусами и . Обозначим через величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна , а площадь внешней фигуры равна — . Эти выражения являются нижней и верхней суммами Дарбу и для интеграла . Так как функция непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого найдется такое разбиение отрезка , что . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

В то же время по определению определенного интеграла

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

Пример 6. Вычислить площадь, ограниченную одним лепестком розы (рис. 40).

Вычисление площади фигуры, ограниченной параметрически заданной кривой

Когда мы выясняли геометрический смысл определенного интеграла, у нас получилась формула, с помощью которой можно найти площадь криволинейной трапеции, ограниченной осью абсцисс, прямыми x = a , x = b , а также непрерывной (неотрицательной или неположительной) функцией y = f ( x ) . Иногда удобнее задавать функцию, ограничивающую фигуру, в параметрическом виде, т.е. выражать функциональную зависимость через параметр t . В рамках данного материала мы покажем, как можно найти площадь фигуры, если она ограничена параметрически заданной кривой.

После объяснения теории и выведения формулы мы разберем несколько характерных примеров на нахождение площади таких фигур.

Основная формула для вычисления

Допустим, что у нас имеется криволинейная трапеция, границами которой являются прямые x = a , x = b , ось O x и параметрически заданная кривая x = φ ( t ) y = ψ ( t ) , а функции x = φ ( t ) и y = ψ ( t ) являются непрерывными на интервале α ; β , α β , x = φ ( t ) будет непрерывно возрастать на нем и φ ( α ) = a , φ ( β ) = b .

Чтобы вычислить площадь трапеции при таких условиях, нужно использовать формулу S ( G ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t .

Мы вывели ее из формулы площади криволинейной трапеции S ( G ) = ∫ a b f ( x ) d x методом подстановки x = φ ( t ) y = ψ ( t ) :

S ( G ) = ∫ a b f ( x ) d x = ∫ α β ψ ( t ) d ( φ ( t ) ) = ∫ α β ψ ( t ) · φ ‘ ( t ) d t

Учитывая монотонное убывание функции x = φ ( t ) на интервале β ; α , β α , нужная формула принимает вид S ( G ) = – ∫ β α ψ ( t ) · φ ‘ ( t ) d t .

Если функция x = φ ( t ) не относится к основным элементарным, то нам понадобится вспомнить основные правила возрастания и убывания функции на интервале, чтобы определить, будет ли она возрастающей или убывающей.

Решение задач на вычисление площади фигуры, которая ограничена параметрически заданной кривой

В этом пункте мы разберем несколько задач на применение формулы, выведенной выше.

Условие: найдите площадь фигуры, которую образует линия, заданная уравнениями вида x = 2 cos t y = 3 sin t .

Решение

У нас есть параметрически заданная линия. Графически ее можно отобразить в виде эллипса с двумя полуосями 2 и 3 . См на иллюстрацию:

Попробуем найти площадь 1 4 полученной фигуры, которая занимает первый квадрант. Область находится в интервале x ∈ a ; b = 0 ; 2 . Далее умножим полученное значение на 4 и найдем площадь целой фигуры.

Вот ход наших вычислений:

x = φ ( t ) = 2 cos t y = ψ ( t ) = 3 sin t φ α = a ⇔ 2 cos α = 0 ⇔ α = π 2 + πk , k ∈ Z , φ β = b ⇔ 2 cos β = 2 ⇔ β = 2 πk , k ∈ Z

При k , равном 0 , мы получим интервал β ; α = 0 ; π 2 . Функция x = φ ( t ) = 2 cos t на нем будет монотонно убывать (подробнее см. статью об основных элементарных функциях и их свойствах). Значит, можно применить формулу вычисления площади и найти определенный интеграл, используя формулу Ньютона-Лейбница:

– ∫ 0 π 2 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π 2 sin 2 t d t = 3 ∫ 0 π 2 ( 1 – cos ( 2 t ) d t = = 3 · t – sin ( 2 t ) 2 0 π 2 = 3 · π 2 – sin 2 · π 2 2 – 0 – sin 2 · 0 2 = 3 π 2

Значит, площадь фигуры, заданной исходной кривой, будет равна S ( G ) = 4 · 3 π 2 = 6 π .

Ответ: S ( G ) = 6 π

Уточним, что при решении задачи выше можно было взять не только четверть эллипса, но и его половину – верхнюю или нижнюю. Одна половина будет расположена на интервале x ∈ a ; b = – 2 ; 2 . В этом случае у нас бы получилось:

φ ( α ) = a ⇔ 2 cos α = – 2 ⇔ α = π + π k , k ∈ Z , φ ( β ) = b ⇔ 2 cos β = 2 ⇔ β = 2 π k , k ∈ Z

Таким образом, при k равном 0 , мы получили β ; α = 0 ; π . Функция x = φ ( t ) = 2 cos t на этом интервале будет монотонно убывать.

После этого вычисляем площадь половины эллипса:

– ∫ 0 π 3 sin t · 2 cos t ‘ d t = 6 ∫ 0 π sin 2 t d t = 3 ∫ 0 π ( 1 – cos ( 2 t ) d t = = 3 · t – sin ( 2 t ) 2 0 π = 3 · π – sin 2 · π 2 – 0 – sin 2 · 0 2 = 3 π

Важно отметить, что можно взять только верхнюю или нижнюю часть, а правую или левую нельзя.

Можно составить параметрическое уравнение данного эллипса, центр которого будет расположен в начале координат. Оно будет иметь вид x = a · cos t y = b · sin t . Действуя так же, как и в примере выше, получим формулу для вычисления площади эллипса S э л и п с а = πab .

Задать окружность, центр которой расположен в начале координат, можно с помощью уравнения x = R · cos t y = R · sin t , где t является параметром, а R – радиусом данной окружности. Если мы сразу воспользуемся формулой площади эллипса, то то у нас получится формула, с помощью которой можно вычислить площадь круга с радиусом R : S к р у г а = πR 2 .

Разберем еще одну задачу.

Условие: найдите, чему будет равна площадь фигуры, которая ограничена параметрически заданной кривой x = 3 cos 3 t y = 2 sin 3 t .

Решение

Сразу уточним, что данная кривая имеет вид вытянутой астроиды. Обычно астроида выражается с помощью уравнения вида x = a · cos 3 t y = a · sin 3 t .

Теперь разберем подробно, как построить такую кривую. Выполним построение по отдельным точкам. Это самый распространенный метод, который применим для большинства задач. Более сложные примеры требуют проведения дифференциального исчисления, чтобы выявить параметрически заданную функцию.

У нас x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t .

Данные функции являются определенными для всех действительных значений t . Для sin и cos известно, что они являются периодическими и их период составляет 2 пи. Вычислив значения функций x = φ ( t ) = 3 cos 3 t , y = ψ ( t ) = 2 sin 3 t для некоторых t = t 0 ∈ 0 ; 2 π π 8 , π 4 , 3 π 8 , π 2 , . . . , 15 π 8 , получим точки x 0 ; y 0 = ( φ ( t 0 ) ; ψ ( t 0 ) ) .

Составим таблицу итоговых значений:

t 0	0	π 8	π 4	3 π 8	π 2	5 π 8	3 π 4	7 π 8	π
x 0 = φ ( t 0 )	3	2 . 36	1 . 06	0 . 16	0	– 0 . 16	– 1 . 06	– 2 . 36	– 3
y 0 = ψ ( t 0 )	0	0 . 11	0 . 70	1 . 57	2	1 . 57	0 . 70	0 . 11	0

t 0	9 π 8	5 π 4	11 π 8	3 π 2	13 π 8	7 π 4	15 π 8	2 π
x 0 = φ ( t 0 )	– 2 . 36	– 1 . 06	– 0 . 16	0	0 . 16	1 . 06	2 . 36	3
y 0 = ψ ( t 0 )	– 0 . 11	– 0 . 70	– 1 . 57	– 2	– 1 . 57	– 0 . 70	– 0 . 11	0

После этого отметим нужные точки на плоскости и соединим их одной линией.

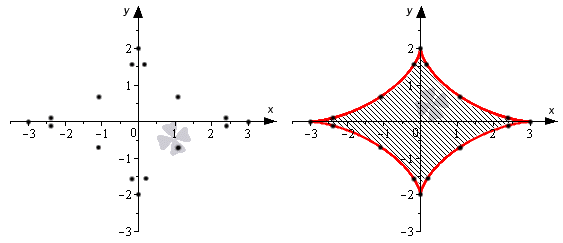
Теперь нам надо найти площадь той части фигуры, что находится в первой координатной четверти. Для нее x ∈ a ; b = 0 ; 3 :

φ ( α ) = a ⇔ 3 cos 3 t = 0 ⇔ α = π 2 + πk , k ∈ Z , φ ( β ) = b ⇔ 3 cos 3 t = 3 ⇔ β = 2 πk , k ∈ Z

Если k равен 0 , то у нас получится интервал β ; α = 0 ; π 2 , и функция x = φ ( t ) = 3 cos 3 t на нем будет монотонно убывать. Теперь берем формулу площади и считаем:

– ∫ 0 π 2 2 sin 3 t · 3 cos 3 t ‘ d t = 18 ∫ 0 π 2 sin 4 t · cos 2 t d t = = 18 ∫ 0 π 2 sin 4 t · ( 1 – sin 2 t ) d t = 18 ∫ 0 π 2 sin 4 t d t – ∫ 0 π 2 sin 6 t d t

У нас получились определенные интегралы, которые можно вычислить с помощью формулы Ньютона-Лейбница. Первообразные для этой формулы можно найти, используя рекуррентную формулу J n ( x ) = – cos x · sin n – 1 ( x ) n + n – 1 n J n – 2 ( x ) , где J n ( x ) = ∫ sin n x d x .

∫ sin 4 t d t = – cos t · sin 3 t 4 + 3 4 ∫ sin 2 t d t = = – cos t · sin 3 t 4 + 3 4 – cos t · sin t 2 + 1 2 ∫ sin 0 t d t = = – cos t · sin 3 t 4 – 3 cos t · sin t 8 + 3 8 t + C ⇒ ∫ 0 π 2 sin 4 t d t = – cos t · sin 3 t 4 – 3 cos t · sin t 8 + 3 8 t 0 π 2 = 3 π 16 ∫ sin 6 t d t = – cos t · sin 5 t 6 + 5 6 ∫ sin 4 t d t ⇒ ∫ 0 π 2 sin 6 t d t = – cos t · sin 5 t 6 0 π 2 + 5 6 ∫ 0 π 2 sin 4 t d t = 5 6 · 3 π 16 = 15 π 96

Мы вычислили площадь четверти фигуры. Она равна 18 ∫ 0 π 2 sin 4 t d t – ∫ 0 π 2 sin 6 t d t = 18 3 π 16 – 15 π 96 = 9 π 16 .

Если мы умножим это значение на 4 , получим площадь всей фигуры – 9 π 4 .

Точно таким же образом мы можем доказать, что площадь астроиды, заданной уравнениями x = a · cos 3 t y = a · sin 3 t , можно найти по формуле S а с т р о и д ы = 3 πa 2 8 , а площадь фигуры, которая ограничена линией x = a · cos 3 t y = b · sin 3 t , считается по формуле S = 3 πab 8 .

Вычисление площадей плоских областей

Вычисление площадей плоских областей

1. Услуги проектирования
2. Двойной интеграл
3. Вычисление площадей плоских областей

Вычисление площадей плоских областей

В соответствии с свойством Интеграл от единичной функции $s(D)=iintlimits_D < dxdy >$.

Найти площадь области , лежащей внутри кривых $left( < x^2+y^2 >right)^2=a^2left( < x^2-y^2 >right),;x^2+y^2=asqrt 2 left( < sqrt < x^2+y^2 >-x >right)$.

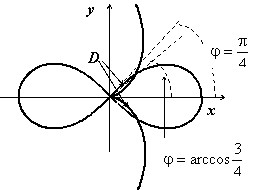
Решение:

Построить эти кривые можно только в полярных координатах; первое уравнение приводится к виду $r=asqrt < cos 2varphi >$, это – лемниската Бернулли; второе – к виду $r=asqrt 2 left( < 1-cos varphi >right)$ – это кардиоида. Решая уравнение $asqrt < cos 2varphi >=asqrt 2 left( < 1-cos varphi >right)$, находим, что точка их пересечения лежит на луче $varphi =arccos (3/4)$.$mathbf < textit < D >> $состоит из двух лунок одинаковой площади; вычислим площадь верхней. При $0leqslant varphi leqslant arccos (3/4)$эта лунка ограничена кардиоидой; при $arccos (3/4)leqslant varphi leqslant pi /4$ – лемнискатой, поэтому $s(D)=iintlimits_D < dxdy >=iintlimits_ < D_ < r,varphi >> < rdrdvarphi >=intlimits_0^ < arccos (3/4) > < dvarphi intlimits_0^ < asqrt 2 (1-cos varphi ) > < rdr >> +intlimits_ < arccos (3/4) >^ < pi /4 > < dvarphi intlimits_0^ < asqrt < 2cos 2varphi >> < rdr >> = \ = intlimits_0^ < arccos (3/4) > < dvarphi cdot left. < frac < r^2 > < 2 >>right|_0^ < asqrt 2 (1-cos varphi ) >> +intlimits_ < arccos (3/4) >^ < pi /4 > < dvarphi cdot left. < frac < r^2 > < 2 >>right|_0^ < asqrt < 2cos 2varphi >> > = \ = a^2intlimits_0^ < arccos (3/4) > < (1-cos varphi )^2dvarphi >+a^2intlimits_ < arccos (3/4) >^ < pi /4 > < cos 2varphi dvarphi >= a^2left. < left( < frac < 3 > < 2 >varphi -2sin varphi +frac < sin 2varphi > < 4 >>right) >right|_0^ < arccos (3/4) >+frac < a^2 > < 2 >left. < sin 2varphi >right|_ < arccos (3/4) >^ < pi /4 >= \ =a^2left( < frac < 3 > < 2 >arccos (3/4)-2sin arccos (3/4)+frac < sin (2arccos (3/4)) > < 4 >>right)+frac < a^2 > < 2 >left( < 1-sin (2arccos (3/4)) >right) = \ = a^2left( < frac < 3 > < 2 >arccos (3/4)-2sqrt < 1-(3/4)^2 >+frac < 1 > < 4 >cdot 2cdot sqrt < 1-(3/4)^2 >cdot frac < 3 > < 4 >>right)+frac < a^2 > < 2 >left( < 1-2cdot sqrt < 1-(3/4)^2 >cdot frac < 3 > < 4 >>right)= \ =frac < a^2 > < 2 >left( < 1-frac < 19sqrt 7 > < 16 >>right)+frac < 3 > < 2 >a^2arccos (3/4) $

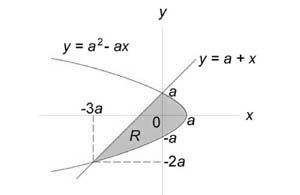
Вычислить площадь области (R,) ограниченной линиями ( < y^2 >= < a^2 >- ax,) (y = a + x.)

Решение:

Площадь области типа (I)

(A = largeintlimits_a^bnormalsize < largeintlimits_ < gleft( x right) >^ < fleft( x right) >normalsize < dydx >> )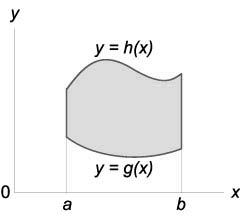

Площадь области типа (II)

(A = largeintlimits_c^dnormalsize < largeintlimits_ < pleft( y right) >^ < qleft( y right) >normalsize < dxdy >> )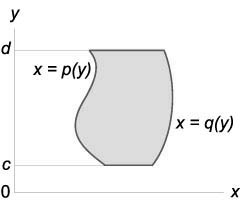

Следовательно, координаты точек пересечения равны $ < x_1 >= 0,;; < y_1 >= a + 0 = a,$ $ < x_2 >= – 3a,;; < y_2 >= a – 3a = – 2a.$ Область (R) представлена на рисунке.

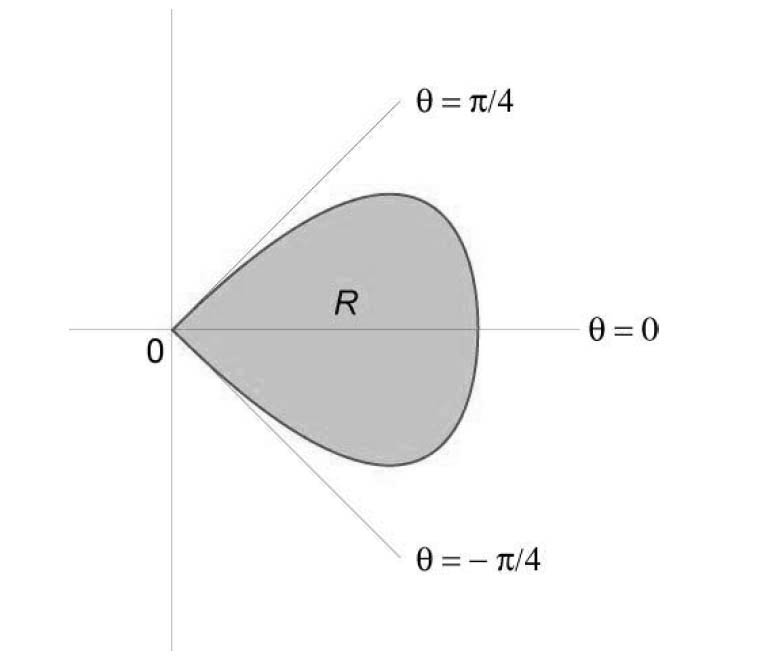
Найти площадь лепестка розы, заданной уравнением (r = cos 2theta.)

Решение:

Рассмотрим лепесток в секторе ( – largefrac < pi > < 4 >normalsize le theta le largefrac < pi > < 4 >normalsize). Область интегрирования имеет вид (R = left[< left( < r,theta >right)|;0 le r le cos 2theta , – largefrac < pi > < 4 >normalsize le theta le largefrac < pi > < 4 >normalsize >right].)

Далее:

Решение задач с помощью алгебры высказываний

Гармонические поля

Введение

Класс Te . Теорема о замкнутости Te

Поверхностный интеграл первого рода и его свойства

Критерий полноты <формулировка>. Лемма о несамодвойственной функции

Критерий полноты

Дифференциальные характеристики векторного поля

Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина

Скалярное поле, производная по направлению, градиент

Вычисление криволинейного интеграла первого рода. Плоский случай

Механические приложения двойного интеграла

Вычисление поверхностного интеграла второго рода

Критерий полноты <формулировка>. Лемма о нелинейной функции

Огравление $Rightarrow $

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/vychislenie-ploschadi-figury-ogranichennoj-paramet/

http://3dstroyproekt.ru/dvojnoj-integral/vychislenie-ploshhadej-ploskih-oblastej

[/spoiler]

Вычислить площадь фигуры, ограниченной линиями

Расчет площади фигуры является, пожалуй, одной из самых сложных задач теории площадей. В школьной геометрии учат находить области базовых геометрических фигур, таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т. д. Однако часто приходится иметь дело с вычислением площадей более сложных форм. Именно при решении таких задач очень удобно использовать интегральное исчисление.

Пример 1.

Найти площадьфигуры,офаниченной линиями Построить чертеж.

Решение:

Найдем точки пересечения параболы и прямой. Приравняем правые части уравнений, задающих функции, и решим полученное уравнение

Фигура, площадь которой нужно найти, изображена на рисунке. Используя приведенную формулу, получим

Ответ: площадь фигуры равна 13,5 кв. ед.

Вычисление площадей плоских фигур в полярной системе координат

Пусть плоская фигура ограничена линией и лучами

тогда ее площадь можно найти по формуле

Если же фигура ограничена линиями и лучами как на рисунке, то площадь фигуры равна

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Пример 2.

Найти площадь фигуры, ограниченной линией, заданной в полярной системе координат уравнением

Решение:

Ответ: площадь данной фигуры 9,5л кв. ед.

Пример З.

Найти площадь фигуры, ограниченной линиями, заданными в полярной системе координат

Решение:

Фигура, площадь которой требуется найти, показана на рисунке.

Найдем точки пересечения окружности и кардиоиды. Решая совместно данные уравнения, получим точки

По рисунку видно, что фигура симметрична. Вычислим площадь половины фигуры, учитывая, что она в свою очередь разделена на части и (см. рисунок).

Ответ: площадь фигуры

Возможно вам будут полезны данные страницы:

Пример 4.3.

Найти площадь фигуры, ограниченной линиями

Решение:

Из чертежа (см. рис. 7) видно, что искомая площадь криволинейного треугольника равна разности двух площадей: каждая из которых находится по геометрическому смыслу определенного интеграла. Решая систему

получаем, что точка В пересечения прямой и кривой имеет координаты (2;4)

Тогда Окончательно,

Данная задача может быть также решена другим способом. По определению определенного интеграла

Если на то интеграл численно равен площади

криволинейной трапеции, ограниченной кривой и прямыми

Другими словами, в данном случае площадь вычисляется посредством проецирования криволинейной трапеции на ось ординат). Теперь возвращаясь к задаче нашего примера, можем записать:

Если криволинейная трапеция ограничена кривой, заданной в параметрическими уравнениями

прямыми и и отрезком оси то ее площадь вычисляется по формуле где и определяются из равенства

Пример 4.5.

1. Вычислить площадь фигуры, ограниченной линиями: и

Решение:

Решая систему уравнений, находим абсциссы точек пересечения эллипса и параболы Каждое из уравнений разрешаем относительно и учетом симметрии области получаем:

Для вычисления первого интеграла применяем подстановку

Второй интеграл вычисляется непосредственно.

Ответ:

Пример 4.6

Вычислить площадь области, ограниченной эллипсом

Решение:

В силу симметричности эллипса относительно координатных осей вычислим часть области, лежащей в первой четверти, кода и следовательно По формуле а) вычисления площади находим

Пример 4.7

Вычислить площадь области, ограниченной лемнискатой

Решение:

Принимая во внимание симметрию линии относительно полярной оси, получаем:

Пример 4.8

Вычислить площадь фигуры, ограниченной прямыми и кривыми

Решение:

Так как максимум функции достигается в точке и равен а функция на отрезке то

Пример 4.9

Вычислить площадь фигуры, лежащей в первом квадранте, ограниченной линиями и осью

Решение:

Функция

составной график которой ограничивает трапецию сверху, является непрерывной на промежутке

Площадь криволинейной трапеции равна

Пример 5.0

Найти площадь астроиды

Решение:

Запишем уравнение астроиды в параметрическом виде

Здесь удобнее вычислить сначала Отсюда

Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.

Определение.

Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).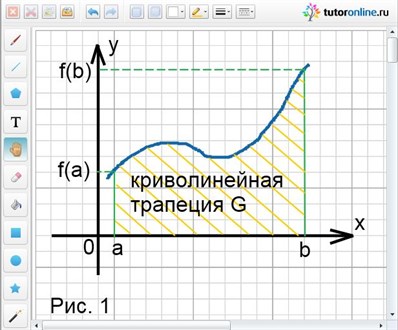

Определенный интеграл ʃ_а^b f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.

То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл  ʃ_а^b f(x)dx.

Таким образом, S(G) = ʃ_а^b f(x)dx.

В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃ_а^b f(x)dx.

Пример 1.

Вычислить площадь фигуры, ограниченной линиями у = х³; у = 1; х = 2.

Решение.

Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.

Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.

Используя формулу S = ʃ_а^b f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:

{у = х³,
{у = 1.

Таким образом, имеем х₁ = 1 – нижний предел и х = 2 – верхний предел.

Итак, S = S_DACE – S_DABE = ʃ₁² x³ dx – 1 = x⁴/4|₁² – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).

Ответ: 11/4 кв. ед.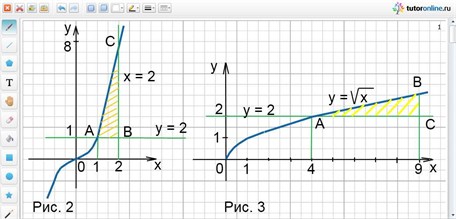

Пример 2.

Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.

Решение.

Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции

у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.

Искомая площадь равна S = ʃ_а^b(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:

{у = √х,
{у = 2.

Таким образом, имеем, что х = 4 = а – это нижний предел.

Итак, S = ∫₄⁹ (√x – 2)dx = ∫₄⁹ √x dx –∫₄⁹ 2dx = 2/3 x√х|₄⁹ – 2х|₄⁹ = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).

Ответ: S = 2 2/3 кв. ед.

Пример 3.

Вычислить площадь фигуры, ограниченной линиями у = х³ – 4х; у = 0; х ≥ 0.

Решение.

Построим график функции у = х³ – 4х при х ≥ 0. Для этого найдем производную у’:

y’ = 3x² – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.

Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции у_min = -16/(3√3) ≈ -3.

Определим точки пересечения графика с осями координат:

если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;

если у = 0, то х³ – 4х = 0 или х(х² – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х₁ = 0, х₂ = 2, х₃ = -2 (не подходит, т.к. х ≥ 0).

Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.

Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.

Так как функция у = х³ – 4х принимает на (0; 2) отрицательное значение, то

S = |ʃ₀² (x³ – 4x)dx|.

Имеем: ʃ₀² (x³ – 4х)dx =(x⁴/4 – 4х²/2)|₀²= -4, откуда S = 4 кв. ед.

Ответ: S = 4 кв. ед.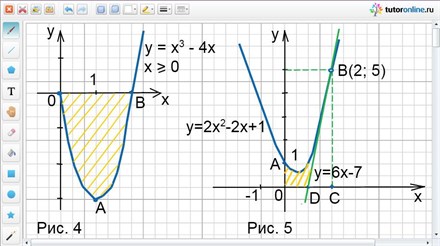

Пример 4.

Найти площадь фигуры, ограниченной параболой у = 2х² – 2х + 1, прямыми  х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х₀ = 2.

Решение.

Сначала составим уравнение касательной к параболе у = 2х² – 2х + 1 в точке с абсциссой х₀ = 2.

Так как производная y’ = 4x – 2, то при х₀ = 2 получим k = y’(2) = 6.

Найдем ординату точки касания: у₀ = 2 · 2² – 2 · 2 + 1 = 5.

Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.

Построим фигуру, ограниченную линиями:

у = 2х² – 2х + 1, у = 0, х = 0, у = 6х – 7.

Г_у =  2х² – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение  2х² – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:

x_b = -b/2a;

x_b = 2/4 = 1/2;

y_b = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).

Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.

Имеем: S_ОAВD = S_OABC – S_ADBC.

Найдем координаты точки D из условия:

6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.

Площадь треугольника DBC найдем по формуле S_ADBC = 1/2 · DC · BC. Таким образом,

S_ADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.

Далее:

S_OABC = ʃ₀²(2x² – 2х + 1)dx = (2x³/3 – 2х²/2 + х)|₀² = 10/3 (кв. ед.).

Окончательно получим: S_ОAВD = S_OABC – S_ADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).

Ответ: S = 1 1/4 кв. ед.

Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Вычисление площади поверхности

Пример 1

Пусть в пространстве задана кусочно-гладкая поверхность $sigma $, однозначно проектирующаяся в область $mathbf { textit { D } } $ на плоскости $mathbf { textit { Оху } } $. Пусть эта поверхность задаётся уравнением $sigma :;z=f(x,y),;(x,y)in D$. Тогда площадь этой поверхности выражается формулой

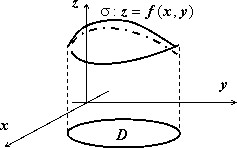
$ s(sigma )=iintlimits_D { sqrt { 1+left( { frac { partial f } { partial x } }right)^2+left( { frac { partial f } { partial y } }right)^2 } dxdy } . $

Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } $ = 2$mathbf { textit { ax } } $ из сферы $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } $ = 4$mathbf { textit { a } } ^ { 2 } $ .

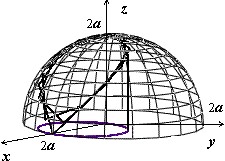
Решение:

На рисунке изображён верхний из этих лепестков. Уравнение поверхности $z=sqrt { 4a^2-x^2-y^2 } ,$ вычисляем производные $frac { partial z } { partial x } =-frac { x } { sqrt { 4a^2-x^2-y^2 } } , quad frac { partial z } { partial y } =-frac { y } { sqrt { 4a^2-x^2-y^2 } } ,$ и $s(sigma )=iintlimits_D { sqrt { 1+frac { x^2+y^2 } { 4a^2-x^2-y^2 } dxdy } } =2aiintlimits_D { frac { dxdy } { sqrt { 4a^2-x^2-y^2 } } } $.

Область $mathbf { textit { D } } $ – сдвинутый на $mathbf { textit { а } } $ единиц по оси $mathbf { textit { Ох } } $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $mathbf { textit { Оху } } $ и $mathbf { textit { Охz } } $:

$s(sigma )=4cdot 2aiintlimits_ { D_ { r,varphi } } { frac { rdrdvarphi } { sqrt { 4a^2-r^2 } } } =8aintlimits_0^ { pi /2 } { dvarphi intlimits_0^ { 2acos varphi } { left( { 4a^2-r^2 }right)^ { -1/2 } rdr } } =-8aintlimits_0^ { pi /2 } { dvarphi left. { left( { 4a^2-r^2 }right)^ { 1/2 } }right|_0^ { 2acos varphi } } = \ =8aintlimits_0^ { pi /2 } { left[ { 2a-2asqrt { 1-cos ^2varphi } }right]dvarphi } =16a^2left. { left( { varphi +cos varphi }right) }right|_0^ { pi /2 } =16a^2left( { pi /2-1 }right)$.

Пример 2

Вычислить площадь cферы радиуса (a.)

Решение:

Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ { { x^2 } + { y^2 } + { z^2 } = { a^2 } } ;; { text { или } ;;z = sqrt { { a^2 } – { x^2 } – { y^2 } } . } $

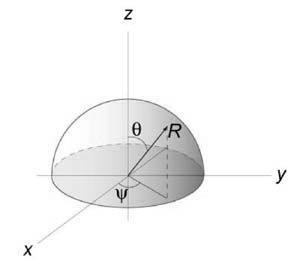
Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } .$

Найдем частные производные. $ { frac { { partial z } } { { partial x } } } = { frac { partial } { { partial x } } sqrt { { a^2 } – { x^2 } – { y^2 } } } = { frac { { – { 2 } x } } { { { 2 } sqrt { { a^2 } – { x^2 } – { y^2 } } } } } = { – frac { x } { z } , } $ $ { frac { { partial z } } { { partial y } } } = { frac { partial } { { partial y } } sqrt { { a^2 } – { x^2 } – { y^2 } } } = { frac { { – { 2 } y } } { { { 2 } sqrt { { a^2 } – { x^2 } – { y^2 } } } } } = { – frac { y } { z } . } $

Подставляя найденные производные, получаем $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } } = { iintlimits_R { sqrt { 1 + frac { { { x^2 } } } { { { z^2 } } } + frac { { { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { sqrt { frac { { { z^2 } + { x^2 } + { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { frac { a } { z } dxdy } . } $

Преобразуем двойной интеграл в полярные координаты. $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { frac { a } { z } dxdy } } = { intlimits_0^ { 2pi } { intlimits_0^a { frac { a } { { sqrt { { a^2 } – { r^2 } } } } rdrdtheta } } } = { aintlimits_0^ { 2pi } { dtheta } intlimits_0^a { frac { { rdr } } { { sqrt { { a^2 } – { r^2 } } } } } } = { – 2pi aintlimits_0^a { frac { { dleft( { { a^2 } – { r^2 } }right) } } { { 2sqrt { { a^2 } – { r^2 } } } } } } = { – 2pi aleft. { left( { sqrt { { a^2 } – { r^2 } } }right) }right|_ { r = 0 } ^a } = { – 2pi aleft( { 0 – a }right) = 2pi { a^2 } . } $

Площадь поверхности полной сферы, соответственно, равна $S = 2 { S_ { largefrac { 1 } { 2 } normalsize } } = 4pi { a^2 } .$