Как найти площадь закрашенной части окружности

Задача B5: площадь закрашенного сектора

В этом уроке мы разберем еще одну задачу B5 на площади секторов из ЕГЭ по математике, однако будьте очень внимательны: на первый взгляд все считается очень просто. Но в самом конце решения многие ученики допускают очень обидную ошибку. Сейчас вы поймете, о чем идет речь. Итак, задача:

Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S /π.

Как решать такую задачу? В первую очередь, поскольку речь идет о площади сектора, нам нужно знать формулу площади круга:

где R — радиус круга. Следовательно, для решения нам потребуется найти этот самый радиус. В данной задаче все очень просто: проводим вертикальный радиус и считаем клеточки.

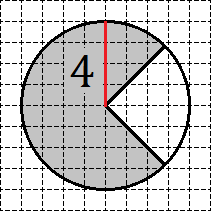
Отсюда сразу получаем, что радиус R = 4. Таким образом, площадь круга S равна:

Обратите внимание: нам очень повезло с радиусом. Потому что в настоящих задачах далеко не всегда верхняя точка окружности лежит в узлах координатной сетки. Однако где-то на окружности обязательно найдется точка с целочисленными координатами, которая точно будет лежать в узле сетки. Вот ее и надо использовать для вычисления радиуса. Давайте посмотрим, каким образом.

Для этого нам потребуется отдельная сетка. Отметим на ней центр окружности (точку O ) и некую гипотетическую точку A , которая должна лежать на нашей окружности. Допустим, это будет выглядеть следующим образом:

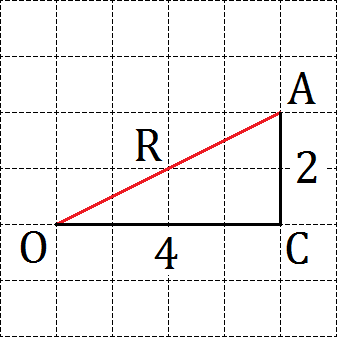
Тогда отрезок OA будет радиусом этой окружности. Как его найти? Достроим до прямоугольного треугольника наш отрезок. Если двигаться вдоль линий координатной сетки, мы получим прямоугольный треугольник OAC с прямым углом C . Разумеется, полученная таким образом точка C не будет лежать на окружности — она лежит где-то внутри. Но этого нам и не требуется. Главное, что мы легко можем найти катеты: OC = 4, AC = 2.

Тогда мы можем найти радиус R (он же — отрезок OA ) по теореме Пифагора:

R 2 = 4 2 + 2 2 = 16 + 4 = 20

И тогда получилось бы, что вместо 16π площадь всего круга равнялась бы 20π. В остальном решение было бы полностью аналогичным, поэтому возвращаемся к нашей исходной задаче. Мы только что нашли площадь круга, а нам надо найти площадь сектора. Давайте схематично перерисуем круг и разделим его на 8 равных частей, как пиццу (стандартная практика в задачах B5). Затем закрашиваем на получившемся рисунке те сектора, которые на исходном чертеже также были закрашены:

Получаем, что закрашенных кусочков было k = 6, а всего их изначально n = 8. Поскольку все части равные, мы можем найти площадь каждого маленького сектора, разделив общую площадь круга на 8:

А поскольку в закрашенном секторе таких кусочков k = 6, то искомая площадь будет равна

S = 6 · S _sec = 6 · 2π = 12π

Но в задаче B5 от нас требуется найти не просто площадь сектора, а величину S /π. Поэтому выполняем последний шаг. Подставляем и получаем:

Это и есть ответ. Так в чем же главная ошибка учеников, которые решают подобные задачи? Дело в том, что многие начинают считать площадь меньшего из секторов, изображенных на рисунке. Однако этот сектор не закрашен. В результате при правильных по существу расчетах многие ученики получают неправильный ответ. Согласитесь, обидная ошибка?

Поэтому рекомендация следующая: внимательно читайте условие задачи B5! Если требуется найти площадь закрашенного сектора, то именно закрашенный сектор и нужно искать. Даже если на чертеже он занимает большую часть круга. А если требуется найти площадь незакрашенного сектора, то об этом обязательно будет указано в условии. Поэтому прежде чем записывать ответ, еще раз проверьте, что от вас требуется: закрашенный сектор или незакрашенный? И тогда дополнительный балл на ЕГЭ по математике вам гарантирован.:)

Круг на клетчатой бумаге

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Так как центральный угол, соответствующий данному сектору, равен 90º, то

2) На клетчатой бумаге изображён круг.

Какова площадь круга, если площадь заштрихованного сектора равна 17?

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

5) На клетчатой бумаге изображен круг площадью 96.

Найдите площадь заштрихованного сектора.

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

Рассмотрим треугольник ABC.

Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) Центральный угол равен 30+45=75°,

площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

10) Центральный угол равен 180-30=150°,

площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

11) Центральный угол равен 60-45=15°,

площадь заштрихованного сектора составляет 1/24 площади круга

12) Центральный угол равен 15+90=105°

Как найти площадь закрашенной части окружности

На клетчатой бумаге с размером клетки 1 × 1 изображён вписанный в окружность угол ABC. Найдите его градусную величину.

Аналоги к заданию № 27890: 26237 27891 509571 Все

На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого см. Поэтому

см 2 .

Хотелось бы более “научного” доказательства. Аргумент “это видно” не достаточен, так как всем видно разное. Спасибо!

На рисунке ВИДНО, что они равны. Или задайте прямые уравнениями и и найдите угол между ними. Но то, что уравнения именно такие, тоже ВИДНО по рисунку. Задания на работу с рисунками предполагают считывание информации с рисунка.

На клетчатой бумаге с размером клетки 1 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.

Треугольник прямоугольный, значит, радиус описанной вокруг него окружности равен половине гипотенузы.

[spoiler title=”источники:”]

http://ege.sdamgia.ru/test?theme=123

[/spoiler]

Первым шагом выполним несколько дополнительных построений:

1) построим полную окружность с центром О и радиусом АВ

2) продолжим отрезки ЕС и ВС до пересечения с окружностью, достроим радиус АО до диаметра AG

Далее вычислим значения некоторых углов:

1) Из Δ ВСО: ∠BCO=180° – (∠СВО+∠СОВ)= 180° – (30°+105°)=45°

2) ∠ACF=∠BCO=45° (вертикальные)

3) ∠ECA=180° – (∠BCO+∠ECB)=180° – (45°+90°)=45°

Ищем значение дуги ВЕ:

1)⌒EA = ⌒AF

2) ⌒ BG = 180°-105°=75°

3) (⌒ BG+⌒AF)/2=∠ACF ⇒ (75°+⌒AF)/2=45°⇒⌒AF=15°

4) ⌒EA = ⌒AF=15°

4) ⌒ BE= ⌒BA-⌒EA=105°-15°=90°

Площадь закрашенной части состоит из площади сегмента ВЕ и площади прямоугольного треугольника ВCЕ.

Площадь сегмента (R=OB=12):

S= πR²/4-S(BOE)=πR²/4 – 72=144π/4-72=36π-72

Площадь треугольника ВCЕ:

Δ ВCE: прямоугольный, ВЕ=12√2, ∠СВЕ=45°-30°=15°

S = 1/2 ⋅ BE²sin15°cos15° = 1/2 ⋅(12√2)²sin15°cos15° =

= 1/2 ⋅144⋅2⋅sin15°cos15°=1/2 ⋅144⋅sin30° =1/2⋅144⋅1/2=36

Площадь закрашенной части:

(36π-72) + 36= 36π – 36 = 36(π-1)

Ответ: Б

СПАСИБО ВСЕМ ЗА РЕШЕНИЯ 🍁🧡 И АКТИВНОСТЬ!

3 октября 2013

В этом уроке мы разберем еще одну задачу B5 на площади секторов из ЕГЭ по математике, однако будьте очень внимательны: на первый взгляд все считается очень просто. Но в самом конце решения многие ученики допускают очень обидную ошибку. Сейчас вы поймете, о чем идет речь. Итак, задача:

Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как решать такую задачу? В первую очередь, поскольку речь идет о площади сектора, нам нужно знать формулу площади круга:

S = πR²

где R — радиус круга. Следовательно, для решения нам потребуется найти этот самый радиус. В данной задаче все очень просто: проводим вертикальный радиус и считаем клеточки.

Отсюда сразу получаем, что радиус R = 4. Таким образом, площадь круга S равна:

S = π · 4² = 16π

Обратите внимание: нам очень повезло с радиусом. Потому что в настоящих задачах далеко не всегда верхняя точка окружности лежит в узлах координатной сетки. Однако где-то на окружности обязательно найдется точка с целочисленными координатами, которая точно будет лежать в узле сетки. Вот ее и надо использовать для вычисления радиуса. Давайте посмотрим, каким образом.

Для этого нам потребуется отдельная сетка. Отметим на ней центр окружности (точку O) и некую гипотетическую точку A, которая должна лежать на нашей окружности. Допустим, это будет выглядеть следующим образом:

Тогда отрезок OA будет радиусом этой окружности. Как его найти? Достроим до прямоугольного треугольника наш отрезок. Если двигаться вдоль линий координатной сетки, мы получим прямоугольный треугольник OAC с прямым углом C. Разумеется, полученная таким образом точка C не будет лежать на окружности — она лежит где-то внутри. Но этого нам и не требуется. Главное, что мы легко можем найти катеты: OC = 4, AC = 2.

Тогда мы можем найти радиус R (он же — отрезок OA) по теореме Пифагора:

R² = 4² + 2² = 16 + 4 = 20

И тогда получилось бы, что вместо 16π площадь всего круга равнялась бы 20π. В остальном решение было бы полностью аналогичным, поэтому возвращаемся к нашей исходной задаче. Мы только что нашли площадь круга, а нам надо найти площадь сектора. Давайте схематично перерисуем круг и разделим его на 8 равных частей, как пиццу (стандартная практика в задачах B5). Затем закрашиваем на получившемся рисунке те сектора, которые на исходном чертеже также были закрашены:

Получаем, что закрашенных кусочков было k = 6, а всего их изначально n = 8. Поскольку все части равные, мы можем найти площадь каждого маленького сектора, разделив общую площадь круга на 8:

S_sec = 16π/8 = 2π

А поскольку в закрашенном секторе таких кусочков k = 6, то искомая площадь будет равна

S = 6 · S_sec = 6 · 2π = 12π

Но в задаче B5 от нас требуется найти не просто площадь сектора, а величину S/π. Поэтому выполняем последний шаг. Подставляем и получаем:

12π : π = 12

Это и есть ответ. Так в чем же главная ошибка учеников, которые решают подобные задачи? Дело в том, что многие начинают считать площадь меньшего из секторов, изображенных на рисунке. Однако этот сектор не закрашен. В результате при правильных по существу расчетах многие ученики получают неправильный ответ. Согласитесь, обидная ошибка?

Поэтому рекомендация следующая: внимательно читайте условие задачи B5! Если требуется найти площадь закрашенного сектора, то именно закрашенный сектор и нужно искать. Даже если на чертеже он занимает большую часть круга. А если требуется найти площадь незакрашенного сектора, то об этом обязательно будет указано в условии. Поэтому прежде чем записывать ответ, еще раз проверьте, что от вас требуется: закрашенный сектор или незакрашенный? И тогда дополнительный балл на ЕГЭ по математике вам гарантирован.:)

Смотрите также:

1. Задача B5: площадь кольца
2. Задача B5: площадь сектора
3. Как сдать ЕГЭ по математике
4. Метод коэффициентов, часть 1
5. Задача B5: метод узлов
6. Сфера, описанная вокруг куба

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой.  90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

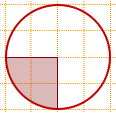
1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Решение:

Так как центральный угол, соответствующий данному сектору, равен 90º, то

S_{сектора}=S_круга:4=60:4=15.

Обратная задача.

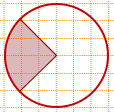2) На клетчатой бумаге изображён круг.

Какова площадь круга, если площадь заштрихованного сектора равна 17?

Решение:

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

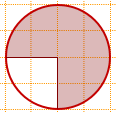3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

Решение:

Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

S_круга=S_{сектора}:(3/4)=21: (3/4)=21·4:3=28.

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Решение:

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

S_круга=S_{сектора}:(1/8)=11: (1/8)=11·8=88.

5) На клетчатой бумаге изображен круг площадью 96.

Найдите площадь заштрихованного сектора.

Решение:

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{незакрашенного сектора}=S_круга:8=96:8=12.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

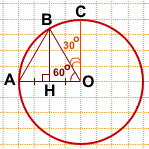Рассмотрим треугольник ABC.

Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

∠BOC=∠AOC-∠AOB=90°-60°=30°.

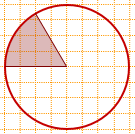6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

Решение:

Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

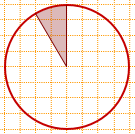7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

Решение:

Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

S_круга=S_{сектора}:(1/12)=24: (1/12)=24·12=288.

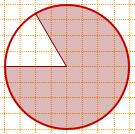8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

Решение:

Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

S_круга=S_{сектора}:(5/6)=60: (5/6)=60·6:5=72°.

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) 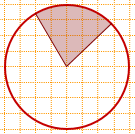Центральный угол равен 30+45=75°,

площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

S_{сектора}=S_круга·(5/24)=S_круга:24·5,

S_круга=S_{сектора}:(5/24)=S_круга: 5·24.

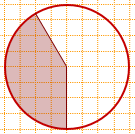10) Центральный угол равен 180-30=150°,

площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

S_{сектора}=S_круга·(5/12),

S_круга=S_{сектора}:(5/12).

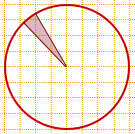11) Центральный угол равен 60-45=15°,

площадь заштрихованного сектора составляет 1/24 площади круга

и т.д.

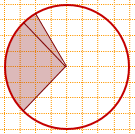12) Центральный угол равен 15+90=105°

(либо 180-30-45=105°),

площадь заштрихованного сектора составляет

1/24+1/4=7/24 и т.д.

Сайты, меню, вход, новости