Как найти площадь закрашенной фигуры полукруга

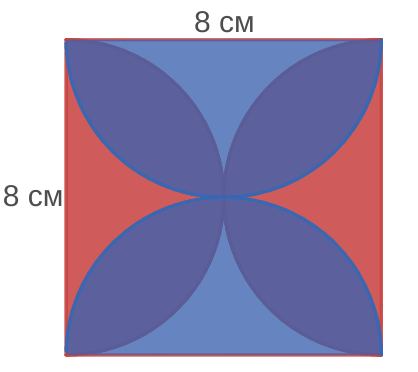
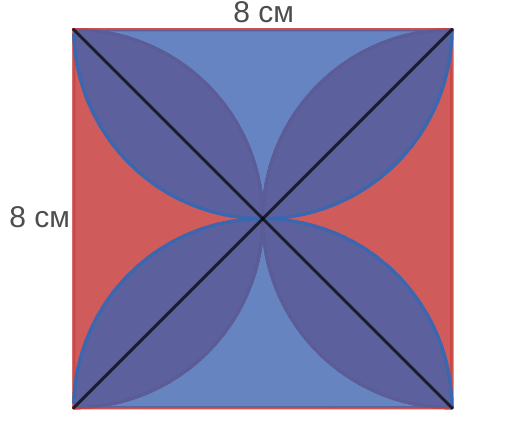
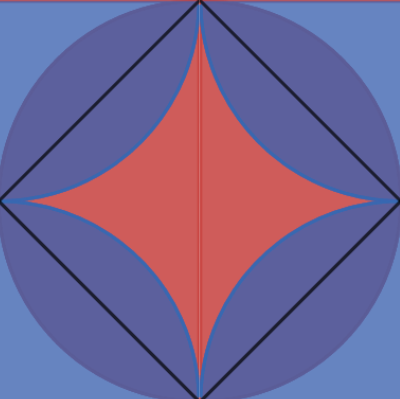
Вычислите площадь закрашенной фигуры, изображенной на рисунке 45.

Задача B5: площадь закрашенного сектора

В этом уроке мы разберем еще одну задачу B5 на площади секторов из ЕГЭ по математике, однако будьте очень внимательны: на первый взгляд все считается очень просто. Но в самом конце решения многие ученики допускают очень обидную ошибку. Сейчас вы поймете, о чем идет речь. Итак, задача:

Задача. Найдите площадь S закрашенного сектора, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S /π.

Как решать такую задачу? В первую очередь, поскольку речь идет о площади сектора, нам нужно знать формулу площади круга:

где R — радиус круга. Следовательно, для решения нам потребуется найти этот самый радиус. В данной задаче все очень просто: проводим вертикальный радиус и считаем клеточки.

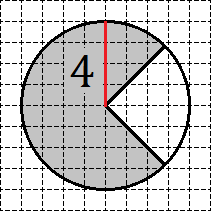
Отсюда сразу получаем, что радиус R = 4. Таким образом, площадь круга S равна:

Обратите внимание: нам очень повезло с радиусом. Потому что в настоящих задачах далеко не всегда верхняя точка окружности лежит в узлах координатной сетки. Однако где-то на окружности обязательно найдется точка с целочисленными координатами, которая точно будет лежать в узле сетки. Вот ее и надо использовать для вычисления радиуса. Давайте посмотрим, каким образом.

Для этого нам потребуется отдельная сетка. Отметим на ней центр окружности (точку O ) и некую гипотетическую точку A , которая должна лежать на нашей окружности. Допустим, это будет выглядеть следующим образом:

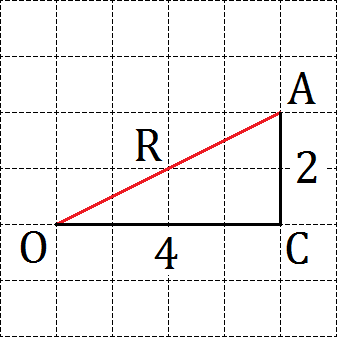
Тогда отрезок OA будет радиусом этой окружности. Как его найти? Достроим до прямоугольного треугольника наш отрезок. Если двигаться вдоль линий координатной сетки, мы получим прямоугольный треугольник OAC с прямым углом C . Разумеется, полученная таким образом точка C не будет лежать на окружности — она лежит где-то внутри. Но этого нам и не требуется. Главное, что мы легко можем найти катеты: OC = 4, AC = 2.

Тогда мы можем найти радиус R (он же — отрезок OA ) по теореме Пифагора:

R 2 = 4 2 + 2 2 = 16 + 4 = 20

И тогда получилось бы, что вместо 16π площадь всего круга равнялась бы 20π. В остальном решение было бы полностью аналогичным, поэтому возвращаемся к нашей исходной задаче. Мы только что нашли площадь круга, а нам надо найти площадь сектора. Давайте схематично перерисуем круг и разделим его на 8 равных частей, как пиццу (стандартная практика в задачах B5). Затем закрашиваем на получившемся рисунке те сектора, которые на исходном чертеже также были закрашены:

Получаем, что закрашенных кусочков было k = 6, а всего их изначально n = 8. Поскольку все части равные, мы можем найти площадь каждого маленького сектора, разделив общую площадь круга на 8:

А поскольку в закрашенном секторе таких кусочков k = 6, то искомая площадь будет равна

S = 6 · S _sec = 6 · 2π = 12π

Но в задаче B5 от нас требуется найти не просто площадь сектора, а величину S /π. Поэтому выполняем последний шаг. Подставляем и получаем:

Это и есть ответ. Так в чем же главная ошибка учеников, которые решают подобные задачи? Дело в том, что многие начинают считать площадь меньшего из секторов, изображенных на рисунке. Однако этот сектор не закрашен. В результате при правильных по существу расчетах многие ученики получают неправильный ответ. Согласитесь, обидная ошибка?

Поэтому рекомендация следующая: внимательно читайте условие задачи B5! Если требуется найти площадь закрашенного сектора, то именно закрашенный сектор и нужно искать. Даже если на чертеже он занимает большую часть круга. А если требуется найти площадь незакрашенного сектора, то об этом обязательно будет указано в условии. Поэтому прежде чем записывать ответ, еще раз проверьте, что от вас требуется: закрашенный сектор или незакрашенный? И тогда дополнительный балл на ЕГЭ по математике вам гарантирован.:)

Круг на клетчатой бумаге

Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.

Для решения обеих задач надо определить величину соответствующего ему центрального угла.

Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.

Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.

Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).

Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).

1) На клетчатой бумаге изображён круг площадью 60.

Найти площадь заштрихованного сектора.

Так как центральный угол, соответствующий данному сектору, равен 90º, то

2) На клетчатой бумаге изображён круг.

Какова площадь круга, если площадь заштрихованного сектора равна 17?

Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.

Следовательно, площадь сектора составляет 1/4 от площади круга: S_круга=S_{сектора}:(1/4)=17·4=68.

3) Найти площадь круга, если площадь заштрихованного сектора равна 21.

Площадь заштрихованного сектора составляет 3/4 площади круга.

Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:

4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?

Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).

Так как 45° составляет от 360° 1/8 часть, то

5) На клетчатой бумаге изображен круг площадью 96.

Найдите площадь заштрихованного сектора.

Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.

S_{закрашенного сектора}=S_{незакрашенного сектора}-S_круга=96-12=84.

А как определить на клетчатой бумаге центральные углы в 60° и 30°?

Можно рассуждать следующим образом.

Рассмотрим треугольник ABC.

Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.

Но AO=BO (как радиусы).

Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.

6) Найти площадь заштрихованного сектора, если площадь круга равна 30.

Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и S_{сектора}=S_круга:6=30:6=5.

7) Найти площадь круга, если площадь заштрихованного сектора равна 24.

Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.

8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.

Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.

Следовательно, на площадь закрашенной части приходится 5/6 круга:

В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.

9) Центральный угол равен 30+45=75°,

площадь заштрихованного сектора составляет

1/12+1/8=5/24 площади круга, то есть

10) Центральный угол равен 180-30=150°,

площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,

11) Центральный угол равен 60-45=15°,

площадь заштрихованного сектора составляет 1/24 площади круга

12) Центральный угол равен 15+90=105°

Как найти площадь закрашенной части окружности

На клетчатой бумаге с размером клетки 1 × 1 изображён вписанный в окружность угол ABC. Найдите его градусную величину.

Аналоги к заданию № 27890: 26237 27891 509571 Все

На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

Отрежем от закрашенной фигуры сектор, отмеченный синим цветом, и добавим к ней сектор, выделенный красным цветом. Указанные секторы равны, поэтому площадь фигуры не изменилась. Следовательно, она равна трём четвертям площади круга, радиус которого см. Поэтому

см 2 .

Хотелось бы более “научного” доказательства. Аргумент “это видно” не достаточен, так как всем видно разное. Спасибо!

На рисунке ВИДНО, что они равны. Или задайте прямые уравнениями и и найдите угол между ними. Но то, что уравнения именно такие, тоже ВИДНО по рисунку. Задания на работу с рисунками предполагают считывание информации с рисунка.

На клетчатой бумаге с размером клетки 1 1 изображён прямоугольный треугольник. Найдите радиус окружности, описанной около этого треугольника.

Треугольник прямоугольный, значит, радиус описанной вокруг него окружности равен половине гипотенузы.

[spoiler title=”источники:”]

http://ege.sdamgia.ru/test?theme=123

[/spoiler]

Есть много задач на нахождение площадей фигур, полученных в результате разнообразных пересечений и наложений многоугольников и окружностей. Такие задачи очень интересно решать, если включить воображение, мысленно достраивая исходные рисунки до полных фигур, применяя соображения симметрии, используя идеи поворота или проводя дополнительные построения.

Решение задач на площади полученные в результате разнообразных пересечений многоугольников и окружностей

Рассмотрим один пример такой задачи.

Задача 1

Найди площадь незакрашенной части квадрата.

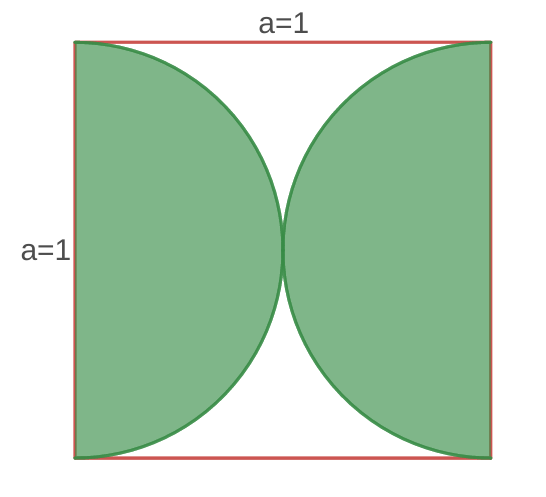
“Разрежем” рисунок на две одинаковые части вертикальной осью симметрии и переставим их. Получим квадрат и вписанный в него зеленый круг.

Тогда площадь незакрашенной части квадрата равна площадь квадрата минус площадь круга с радиусом 0.5.

 Задача 2

Еще один пример:

Найди площадь закрашенной фиолетовым цветом фигуры См. исходный рис. слева).

 

Как можно быстро решить такую задачу?

1. Проведем диагонали исходного квадрата, получим второй рис. 
2. “Разрежем” его на две одинаковые части вертикальной осью симметрии и переставим их. Работать будем с третьим рисунком.
3. Из площади получившегося после преобразования картинки круга (с радиусом 4), вписанного в большой квадрат,  вычтем площадь малого квадрата (он обведен на 3-м рисунке черным).
4. Полученную площадь удвоим.
5. Искомая площадь равна примерно 36,5 кв. см. Точнее площадь даст формула.

Коллекция Фигуры и формы

 Такие вот вызовы можно найти на Pinterest

Формы и фигуры с помощью аналитических записей

Отдельная задача – “нарисовать” такие чертежи с помощью аналитических записей в Desmos.

Такой рисунок в качестве заставки к активности создал с помощью функций и неравенств ученик 11 класса TKVG Валерий Чернов.

Использованы уравнение и неравенство окружности, квадратичные функции, заданные на отрезке, неравенства с модулем.

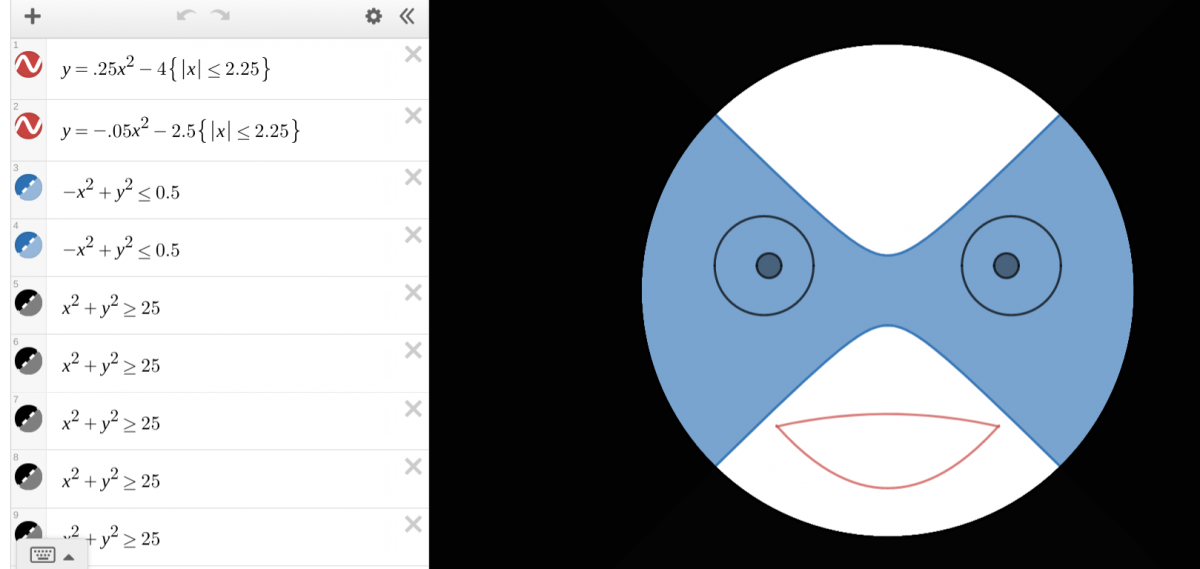
Вообще тема “рисования” окружностями и кругами очень интересна для освоение учениками именно с использованием Desmos.

Впервые уравнение окружности для необычных задач мной было использовано в этой статье!

Уроки в Desmos продолжаются… Повесь ягоду на ветку!

Вот тот самый апплет

Добавь на ветки ягоды! 

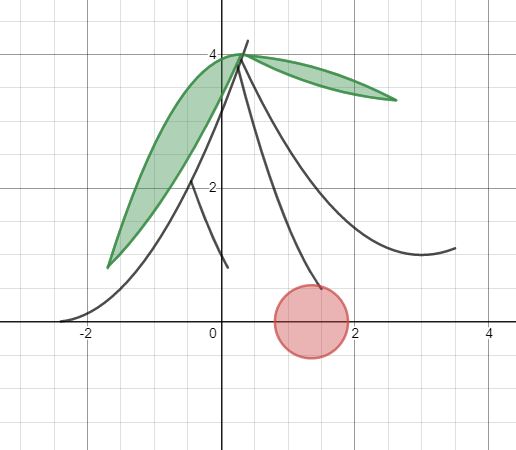
Упражнения на уравнение и неравенство окружности: круг и полукруг

Круг и полукруг

Фигура 5

Рассмотрим еще несколько задач на создание таких во рисунков с использованием в аналитических записях уравнения окружности…

Фигура 1

Фигура 2

Фигура 3

Квадрат создается с помощью знакомых уже таблиц и полигонов

Чтобы внутри квадрата “нарисовать” два полукруга, зададим их с помощью записей: неравенства окружности и неравенства для обозначения области его задания

Для “прорисовки” кругового сектора начнем с создания угла, сделаем это при помощи двух отрезков

Для того, чтобы “нарисовать” сектор и “закрасить” его черным, прибегнем к записям неравенствами

Еще одна задача: требуется создать довольно сложную картинку, состоящую из нескольких закрашенных разными цветами областей. Начнем с закрашенного квадрата (полигон), сложного цвета добиваемся последовательным “наложением” цветов: красного и синего.

Пересечение двух полукругов даст требуемый фиолетовый цвет.

Продолжение следует…

Обновление на 25.11.19

Продолжаются уроки математики с использованием активностей в TeacherDesmos, разработанных учениками нашей гимназии.
В 8б прошел урок математики по сценарию, предложенному Валерием Черновым, учеником G2.2.

Предложенные задания, вызвали интерес у ребят. В течение урока они обсуждали и предлагали разные варианты решения задач.
Сегодня этот же урок был проведен в том же классе, где учится сам Валерий, естественно, он был главным экспертом по этой теме.

Публикации по теме

• Идеи заданий с подвижными отрезками
• Виртуальный геоборд своими руками
• От бумаги к цифре: утренние ремиксы
• Мондриан как артефакт
• Ремикс-проект начинается с рамы
• Клетчатая Ёлка и новогодние ремиксы
• Математическая задача как вызов. Уроки в Desmos
• Инструкция: как создать “объект в зеркале” в среде Desmos
• Курс Desmos-математики стартовал!
• Математики больше не плачут, они анализируют проблемы
• Polygon: от подвижных геометрических фигур до картин
• Страсть к кругам и окружностям
• Задачи на оптимизацию — с помощью ползунков Desmos
• Списки? А для чего они нужны? Потренируемся?
• О “Розе ветров” и других визуализациях-ремиксах в Desmos
• По следам курса Desmos-математики: бери и делай!

Содержание:

1.      Модуль
1: Основные формулы площадей.

2.      Модуль
2: Методы нахождения площадей.

3.      Модуль
3: Задачи с решением.

4.      Модуль
4: Задачи для закрепления.

5.      Модуль
5: Задачи для самостоятельной работы и зачета.

Модуль
1. Теоретическая часть

1.1.Основные
определения и формулы для площадей фигур.

 Прямоугольник.

Прямоугольником
называется четырехугольник, у которого все углы равны. Все углы в
прямоугольнике прямые, т.е. составляют 90°.Площадь прямоугольника равна
произведению его сторон .

Квадрат.

Квадратом
называется параллелограмм с
прямыми углами и равными сторонами. Квадрат есть частный вид прямоугольника, а
также частный вид ромба. См. также площадь ромба.
Площадь квадрата равна квадрату длины его стороны. Или половине квадрата
диагонали.

;     

Трапеция.

Трапецией называется
четырехугольник, у которого две стороны параллельны, а две другие не
параллельны. Площадь трапеции равна произведению полусуммы ее
оснований на высоту.

 Площадь трапеции равна произведению её средней
линии на высоту. 

Параллелограмм.

Параллелограммом называется
четырехугольник, у которого противоположные стороны попарно
параллельны. Площадь параллелограмма равна произведению его
основания  на высоту.

Площадь параллелограмма равна произведению двух соседних его
сторон на синус угла между ними.  

Правильный многоугольник.

Для
того чтобы вычислить площадь правильного многоугольника его разбивают
на равные треугольники с общей вершиной в центре вписанной окружности. А
площадь правильного многоугольника равна произведению его полупериметра
на радиус вписанной окружности правильного
многоугольника.

Выпуклый четырёхугольник.

 Площадь выпуклого четырёхугольника равна половине произведения
его диагоналей на синус угла между ними.  

 Площадь четырёхугольника, вписанного в окружность, равна корню
квадратному из произведения разностей полупериметра этого четырёхугольника и
всех его сторон

Ромб.

Ромбом называется параллелограмм с
равными сторонами. Квадрат есть частный вид ромба. У квадрата диагонали равны.
См. также площадь квадрата. Площадь
ромба равна половине произведения его диагоналей.

 Площадь ромба равна произведению
квадрата его стороны на синус одного из его углов.  

Сектор.

Сектор
круга, окружности — это часть круга, окружности ограниченная
дугой и двумя радиусами, проведенными к концам дуги. Площадь сектора
круга равна произведению половины длины дуги
сектора  на радиус круга.

 Площадь кругового сектора равна произведению площади единичного
сектора (сектор, соответствующий центральному углу с мерой равной единице) на
меру центрального угла, соответствующего данному сектору ( формулы для случаев градусной и радианной мер центральных
углов).

Окружность.

Окружность есть
геометрическое место точек плоскости, равноудаленных от одной ее точки. Равные
отрезки, соединяющие центр с точками окружности, называются радиусами. Круг
есть часть плоскости, лежащая внутри окружности. Площадь круга равна
произведению полуокружности на радиус.

Площадь
сегмента круга, окружности.

Сегмент круга, окружности — это
часть круга, окружности,
ограниченная дугой и стягивающей ее хордой.

Площадь сегмента круга, окружности
находится, как разность площади сектора и площади равнобедренного треугольника выраженную через угол.

Площадь кольца.

Площадь
кольца через радиусы находится как произведение числаπ на разность
квадратов внешнего и внутреннего радиусов кольца.

Площадь кольца через
диаметры находится как произведение одной четвертой числа π на
разность квадратов внешнего и внутреннего диаметров кольца.

 Площадь кругового кольца равна удвоенному произведению числа
“пи”, среднего радиуса кольца и его ширины. 

Площадь сектора кольца.

Сектор
кольца — это часть круга, окружности ограниченная дугами разных радиусов и
двумя линиями радиусами, проведенными к концам дуги большего радиуса.

Площадь сектора кольца вычисляется
как разность площадей большего и меньшего секторов круга.

Площадь сектора кольца если угол в
градусах, вычисляется как произведение числа π на отношение угла
сектора к углу полной окружности 360° и на разность квадратов большего и
меньшего радиусов.

Площадь треугольника.

Треугольник образуется
соединением отрезками трех точек, не лежащих на одной прямой. При этом точки
называются вершинами треугольника, а отрезки – его сторонами. Площадь
треугольника равна произведению половины основания треугольника на его
высоту.

Площадь треугольника по формуле
Герона равна корню из произведения разностей полупериметра треугольника
(p) и каждой из его сторон.

Если
известно две стороны треугольника и угол
между ними, то площадь данного треугольника вычисляется, как половина
произведения этих сторон умноженная на синус угла между ними.

Если
один из углов прямой, то треугольник – прямоугольный. Площадь прямоугольного
треугольника равна половине произведения катетов треугольника.

Площадь равнобедренного треугольника
вычисляется по классической формуле площади
треугольника — произведение половины
основания треугольника на его высоту. Высоту мы подставим в эту формулу
из формулы высоты равнобедренного
треугольника.

 Площадь
равностороннего треугольника вычисляется по классической формуле площади
треугольника — произведение половины
основания треугольника на его высоту. Высоту мы подставим в эту формулу
из формулы высоты равностороннего
треугольника

Площадь треугольника равна отношению произведения
квадрата его стороны на синусы прилежащих углов к удвоенному синусу
противолежащего угла. 

Площадь треугольника равна отношению произведения
квадрата его высоты на синус угла, из вершины которого проведена эта высота, к
удвоенному произведению синусов двух других углов.

 Площадь треугольника равна произведению квадрата
его полупериметра на тангенсы половин всех углов треугольника. 

 Площадь
треугольника равна отношению произведения всех его сторон к четырём радиусам,
описанной около него окружности. 

 Площадь треугольника равна удвоенному
произведению квадрата радиуса, описанной около него окружности, и синусов всех
его углов.

 Площадь треугольника (многоугольника) равна
произведению его полупериметра и радиуса окружности, вписанной в этот
треугольник (многоугольник). 

 Площадь треугольника равна произведению квадрата
радиуса вписанной окружности на котангенсы половин всех углов треугольника.

Шар и сфера.

 Шаровой,
или сферической поверхностью (иногда просто сферой) называется геометрическое
место точек пространства, равноудаленных от одной точки – центра шара. Площадь
поверхности сферы равна учетверенной площади большого круга:

Куб.

Прямоугольный параллелепипед,
все грани которого – квадраты, называется кубом. Все ребра куба равны,
а площадь поверхности куба равна сумме площадей шести его граней, т.е.площади квадрата со
стороной H умноженной на шесть. Площадь поверхности куба равна.

Конус.

Круглый конус может
быть получен вращением прямоугольного треугольника вокруг
одного из его катетов, поэтому круглый конус называют также конусом вращения.

Боковая площадь поверхности круглого
конуса равна произведению половины окружности основания на образующую.

Цилиндр.

Цилиндрической
поверхностью называется поверхность, образуемая прямой, сохраняющей одно и тоже
направление и пересекающей направляющую линию. Цилиндр —
круговой если в основании его лежит круг. Площадь боковой поверхности круглого
цилиндра равна произведению длины окружности основания
на высоту.

Прямоугольный параллелепипед.

Параллелепипедом
называется призма, основание которой параллелограмм. Параллелепипед
имеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые
грани которого — прямоугольники, называется прямым. Прямой параллелепипед у
которого все шесть граней прямоугольники, называется
прямоугольным. Площадь поверхности прямоугольного
параллелепипеда равна удвоенной сумме площадей трех граней этого
параллелепипеда.

Усеченный конус.

Усеченный
конус получится, если в конусе провести сечение, параллельное основанию.
Тело ограниченное этим сечением, основанием и боковой поверхностью конуса
называется усеченным конусом. Боковая площадь поверхности усеченного
конуса вычисляется по формуле.

Шаровой сегмент.

Часть
шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или
сферическим сегментом. Основанием шарового сегмента называется круг ABCD.
Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра,
восстановленного из центра N основания до пересечения с поверхностью
шара. Точка M называется вершиной шарового сегмента. Площадь
поверхности шарового сегмента равняется произведению его высоты на
окружность большого круга шара.

Шаровой
слой.

 Шаровой слой — это часть шара,
заключенная между двумя секущими параллельными плоскостями. Шаровой пояс или Шаровая
зона — это кривая поверхность шарового слоя. Круги ABC и DEF это основания
шарового пояса. Расстояние между основаниями это высота шарового слоя. Кривая
поверхность шарового слоя равна произведению его высоты на окружность
большого круга шара.

Шаровой сектор.

Шаровой
сектор — это часть шара, ограниченная кривой поверхностью шарового
сегмента и конической поверхностью основанием которой служит основание
сегмента, а вершиной — центр шара. Поверхность шарового сектора складывается из
кривых поверхностей шарового сегмента и конуса. Зная радиус основания сегмента
и конуса r при помощи теоремы Пифагора и прямоугольного треугольника
получим высоты сегмента и конуса:

1.2.Справочные
таблицы «Площади плоских фигур, площади поверхности и объема тел вращения»

Модуль
2.  Методы нахождения площади плоских фигур.

Рассмотрим несколько способов нахождения
площади плоских фигур:

·        
формула Пика,

·        
метод обводки.

1.1 
Формула Пика.

Формула, при помощи которой можно находить площадь фигуры
построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник,
многоугольник). Об этой формуле обычно рассказывается применительно к
нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и
вершинах)

N – количество узлов внутри  треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём
площадь треугольника:                     Отметим узлы:

                      

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Пример 1. Найдём площадь параллелограмма:            
Отметим узлы:

               

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Пример 2. Найдём площадь трапеции:                      Отметим
узлы:

                      

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Пример 3. Найдём площадь многоугольника:                     
Отметим узлы:

          

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма,
треугольника проще и быстрее по соответствующим формулам площадей этих фигур.
Но знайте, что можно  это делать и таким образом.  А вот когда дан многоугольник, у которого пять и более углов эта
формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их
площади. При помощи формулы Пика такие задачи решаются за минуту. Например,
найдём площадь фигуры:

                               

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

1.2 Метод обводки.

1. Достроить
   искомую фигуру до прямоугольника.
2. Найти
   площадь всех получившихся дополнительных фигур и площадь самого
   прямоугольника.
3. Из
   площади прямоугольника вычесть сумму площадей всех лишних фигур.

Бывает,
что не так-то просто рассчитать, сколько клеток в нужном отрезке. Вот смотри, треугольник:

Вроде бы даже прямоугольный и S=12⋅abS=​2​​1​​⋅ab, но чему
тут равно aa, и чему
равно bb? Как узнать?
Применим для полной ясности оба способа

I способ.

Найдем  по
теореме Пифагора из ΔADC а  по
теореме Пифагора из ΔBCE.
На  листе в клетку легко посчитать длину катетов.

Итак:

Значит, 

Теперь 

 Значит, 

Подставляем в формулу:

Значит, 

II способ 

Нужно окружить нашу фигуру прямоугольником. Вот
так:

Получился
один (нужный) треугольник внутри и три ненужных треугольника снаружи. Но
площади этих ненужных треугольников легко считаются на листе в клетку. Посчитаем
их, а потом просто вычтем из целого прямоугольника.

Итак,                             

Почему же этот способ лучше? Потому что он работает
и для любых фигур. К примеру, нужно посчитать площадь такой фигуры:

Окружаем
ее прямоугольником и снова получаем одну нужную, но сложную площадь и много
ненужных, но простых.

А теперь чтобы найти
площадь  просто находим площадь прямоугольника и вычитаем из него оставшуюся
площадь фигур на клетчатой бумаге.

 

Значит, 

Вот и ответ: 

Модуль
3: Задачи с решением.

1.      Найдите площадь четырёхугольника, изображённого
на клетчатой бумаге 
с размером клетки 1 см * 1 см. Ответ
дайте в квадратных сантиметрах.

Решение:
Разобьём четырёхугольник
диагональю РС на два треугольника. Диагональ эта хороша тем, что идёт под
углом 45° к горизонту. Проведём через точки А и В прямые, параллельные диагонали.

Если на верхней прямой взять любую точку Т, то площадь треугольника РТС окажется равной площади треугольника РАС, т.к. основание РС у них общее,
а высоты, проведённые к РС, равны. Такие же рассуждения
о точке К.

Таким образом, если удачно разместить точки Т и К, как на рисунке
выше, то 

S_ACBP = S_PAC + S_PBC = S_PTC + S_PKC = S_TKP = 0,5·6·3 = 9

Ответ: 9

Возможны и другие варианты
расположения точек Т и
К:

2.      Найдите
площадь фигуры, изображенной на рисунке, считая стороны квадратных клеток
равными единице.

Решение:

Отрежем у данной фигуры все полукруглые части (выпуклости),
которые выходят за рамки квадрата 4·4, и аккуратно упакуем их
на свободные в квадрате места.
Площадь данной причудливой фигуры просто равна площади квадрата 4·4 =
16.
Ответ: 16

3.     
Найдите площадь четырехугольника, изображенного на клетчатой
бумаге с размером клетки 1 см * 1 см. Ответ дайте в квадратных сантиметрах.

Решение:

Опишем около неё прямоугольник.

Из площади прямоугольника (в данном случае это квадрат) вычтем
площади полученных простых фигур:

Ответ: 4,5

4.      Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки
1см×1см. Ответ дайте в квадратных сантиметрах.

5.      Найдите
площадь треугольника, изображенного на клетчатой бумаге с размером клетки
1см×1см. Ответ дайте в квадратных сантиметрах.

6.      На
клетчатой бумаге нарисован круг площадью 93. Найдите площадь заштрихованного
сектора.

7.      На
клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 9.
Найдите площадь заштрихованной фигуры.

8.      Найдите
(в см²) площадь S
фигуры, изображенной на клетчатой бумаге с размером
клетки 1см×1см. В ответе запишите S/π.

9.      Найдите
площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
1см×1см. Ответ дайте в квадратных сантиметрах.

Модуль
4. Задачи для закрепления.

1.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток равными 1.

2.
Найдите площадь треугольника ABC,
считая стороны квадратных клеток равными 1.

3.
Найдите площадь прямоугольника ABCD,
считая стороны квадратных клеток равными 1.

4.
Найдите площадь ромба ABCD,
считая стороны квадратных клеток равными 1.

5.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток равными 1.

6.
Найдите площадь трапеции ABCD,
считая стороны квадратных клеток равными 1.

7.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток равными 1.

8.
Найдите площадь четырехугольника ABCD,
считая стороны квадратных клеток равными 1.

9.
Найдите площадь S сектора,
считая стороны квадратных клеток равными 1. В ответе укажите .

10.
Найдите площадь S кольца,
считая стороны квадратных клеток равными 1. В ответе укажите .

11.  Найдите площадь треугольника, вершины которого имеют
координаты (1, 1), (4,4), (5, 1).

12.
Найдите площадь четырехугольника, вершины которого имеют координаты (1, 0), (0,
2), (4, 4), (5, 2).

13. Найдите площадь S круга,
изображенного на рисунке. В ответе укажите . Размер каждой клетки 1
см ×1 см. Ответ дайте в квадратных сантиметрах.

14. Найдите площадь S круга,
описанного около прямоугольника ABCD. Размер каждой клетки на чертеже
равен 1см *1см. В ответе укажите   (в кв. см).

15. В ромб ABCD, площадь которого
равна  , вписан круг. Найдите
площадь круга, если размер каждой клетки на чертеже равен 1см *1см.

16.Найдите площадь S круга,
описанного около прямоугольника ABCD. Размер каждой клетки на чертеже
равен 1см *1см. В ответе укажите  (в кв. см).

17. Найдите площадь круга, описанного
около прямоугольного треугольника АВС. Размер каждой клетки на чертеже
равен 1см *1см. В ответе укажите  ( в кв. см).

18. Найдите площадь круга, описанного
около прямоугольного треугольника АВС. Размер каждой клетки на чертеже
равен 1см*1см. В ответе укажите  (в кв. см).

19. Найдите площадь S круга,
описанного около четырехугольника, изображенного на рисунке. В ответе укажите  . Размер каждой клетки 1
см × 1 см. Ответ дайте в сантиметрах.

20. Найдите площадь S круга,
описанного около четырехугольника, изображенного на рисунке. В ответе укажите  .  Размер каждой клетки 1
см × 1 см. Ответ дайте в сантиметрах.

21. Найдите площадь S круга,
изображенного на рисунке. В ответе укажите . Размер каждой клетки 1
см ×1 см. Ответ дайте в квадратных сантиметрах.

22. Найдите площадь S сектора. В
ответе укажите . Размер каждой клетки 1
см ×1 см. Ответ дайте в квадратных сантиметрах.

23. Найдите площадь S заштрихованной
части кругового сектора АОВ. Размер каждой клетки на чертеже равен 1см *1см.
В ответе укажите  (в кв. см).

24.Найдите площадь круга, описанного около
прямоугольника АВСD. Размер каждой клетки на чертеже равен 1см 1см.
В ответе укажите  (в кв. см).

25. Два одинаковых круга касаются друг
друга и сторон прямоугольника ABCD. Найдите площадь одного круга, если площадь
прямоугольника равна  .

26. Две одинаковых окружности касаются
друг друга и сторон прямоугольника ABCD. Найдите периметр прямоугольника, если
длина каждой окружности равна 3,6

27. Диаметр полукруга совпадает со
стороной прямоугольника ABCD, а 3 другие стороны прямоугольника касаются
полукруга. Найдите длину полуокружности, если периметр прямоугольника равен .

 

Модуль
5. Задачи для самостоятельных и зачетных работ.

1.       На клет­ча­той
бу­ма­ге с клет­ка­ми раз­ме­ром 1 см  1 см
изоб­ра­же­на фи­гу­ра (см. ри­су­нок). Най­ди­те ее пло­щадь в квад­рат­ных
сан­ти­мет­рах.

2.      Най­ди­те пло­щадь квад­ра­та ABCD, счи­тая сто­ро­ны квад­рат­ных
кле­ток рав­ны­ми 1.

3.      Най­ди­те пло­щадь квад­ра­та, вер­ши­ны ко­то­ро­го
имеют ко­ор­ди­на­ты (4;3), (10;3), (10;9), (4;9).

4.      Во сколь­ко раз пло­щадь квад­ра­та, опи­сан­но­го
около окруж­но­сти, боль­ше пло­ща­ди квад­ра­та, впи­сан­но­го в эту окруж­ность?

5.      В пря­мо­уголь­ни­ке рас­сто­я­ние от точки пе­ре­се­че­ния
диа­го­на­лей до мень­шей сто­ро­ны на 1 боль­ше, чем рас­сто­я­ние от нее до
боль­шей сто­ро­ны. Пе­ри­метр пря­мо­уголь­ни­ка равен 28. Най­ди­те мень­шую
сто­ро­ну пря­мо­уголь­ни­ка.

6.      На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1
см  1 см изоб­ра­жен па­рал­ле­ло­грамм (см. ри­су­нок).
Най­ди­те его пло­щадь в квад­рат­ных сан­ти­мет­рах.

7.      Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных
сан­ти­мет­рах.

8.      Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных
сан­ти­мет­рах.

9.      Най­ди­те пе­ри­метр че­ты­рех­уголь­ни­ка , если сто­ро­ны квад­рат­ных кле­ток равны .

10.  На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1
см  1 см изоб­ра­же­на тра­пе­ция (см. ри­су­нок).
Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

11.  На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1
см  1 см изоб­ра­же­на тра­пе­ция (см. ри­су­нок).
Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

12.  Най­ди­те пло­щадь тра­пе­ции, вер­ши­ны ко­то­рой
имеют ко­ор­ди­на­ты (1;1), (10;1), (8;6), (5;6).

13.  Най­ди­те вы­со­ту тра­пе­ции , опу­щен­ную из вер­ши­ны , если сто­ро­ны квад­рат­ных кле­ток равны .

14.  На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром
1 см  1 см изоб­ра­же­на фи­гу­ра (см. ри­су­нок).
Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

15. 
Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка,
вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты (8;0), (10;8), (2;10), (0;2).

16.    Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных
сан­ти­мет­рах.

17.  Най­ди­те
пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром
клет­ки 1 см  1
см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

18.   Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

19. 
Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на
клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1
см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

20.   Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го
на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах

21.   На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1 изоб­ражён
тре­уголь­ник. Най­ди­те ра­ди­ус опи­са­ной около него окруж­но­сти.

22.   На клет­ча­той бу­ма­ге на­ри­со­ва­ны два круга. Пло­щадь
внут­рен­не­го круга равна 11. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

23. 
Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, вер­ши­ны
ко­то­ро­го имеют ко­ор­ди­на­ты (1;7), (8;2), (8;4), (1;9).

24.   Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры на ко­ор­ди­нат­ной
плос­ко­сти.

25.  Точки O(0;
0), A(10; 0), B(8; 6), C(2; 6) яв­ля­ют­ся вер­ши­на­ми
тра­пе­ции. Най­ди­те длину ее сред­ней линии DE.

26.  Най­ди­те (в см²) пло­щадь S за­кра­шен­ной фи­гу­ры,
изоб­ра­жен­ной на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см  1 см (см. рис.). В от­ве­те за­пи­ши­те .

27.   Най­ди­те пло­щадь сек­то­ра круга ра­ди­у­са , цен­траль­ный угол ко­то­ро­го равен 90°

28.  .  Най­ди­те
цен­траль­ный угол сек­то­ра круга ра­ди­у­са , пло­щадь ко­то­ро­го равна . Ответ дайте в гра­ду­сах.

29.  На клет­ча­той бу­ма­ге на­ри­со­ва­но два круга. Пло­щадь
внут­рен­не­го круга равна 1. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

30.  На клет­ча­той бу­ма­ге на­ри­со­ва­но два круга. Пло­щадь
внут­рен­не­го круга равна 9. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

Зачет

№1

Найдите площадь окрашенной фигуры,
изображенной на чертеже. Размер каждой клетки равен 1см *1см.
Ответ дайте в квадратных сантиметрах.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

№2

Найдите площадь окрашенной фигуры,
изображенной на чертеже. Размер каждой клетки равен 1см *1см.
Ответ дайте в квадратных сантиметрах.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

№3

В детском саду дети делали аппликации
родителям в подарок. Найдите площадь аппликации (окрашенной фигуры),
изображенной на чертеже. Размер каждой клетки равен 1см*1см.
Ответ дайте в квадратных сантиметрах.

1.

2.

3.

4.

5.

№4  В детском саду дети делали фото- рамки
родителям в подарок. Найдите площадь фото-рамки (окрашенной фигуры),
изображенной на чертеже. Размер каждой клетки равен 1см *1см.
Ответ дайте в квадратных сантиметрах.

6.

7.

8.

9.

10