СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Поиск
?
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 9 1–9
Добавить в вариант
Тип 7 № 323079
i
На рисунке изображён график функции y = f(x). Функция
— одна из первообразных функции y = f(x). Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Видеокурс
·
Помощь
Тип 7 № 323080
i
На рисунке изображён график некоторой функции y = f(x). Функция
— одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323080: 323383 323475 323477 … Все
Решение
·
3 комментария
·
Видеокурс
·
Помощь
Тип 7 № 323283
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323373
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323375
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323379
i
На рисунке изображён график функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323079: 323283 323373 323375 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323383
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323080: 323383 323475 323477 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323475
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323080: 323383 323475 323477 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Тип 7 № 323477
i
На рисунке изображён график некоторой функции
Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
Аналоги к заданию № 323080: 323383 323475 323477 … Все
Решение
·
Прототип задания
·
Видеокурс
·
Помощь
Всего: 9 1–9
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Тема 7.
Взаимосвязь функции и ее производной
7
.
08
Первообразная и площадь под кривой
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
взаимосвязь функции и ее производной
Решаем задачи
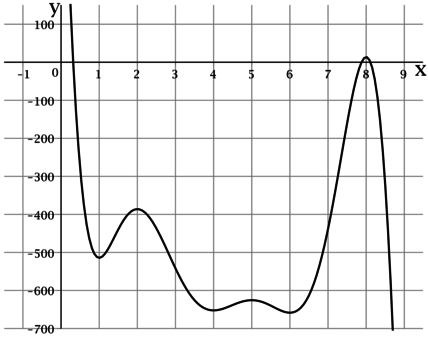
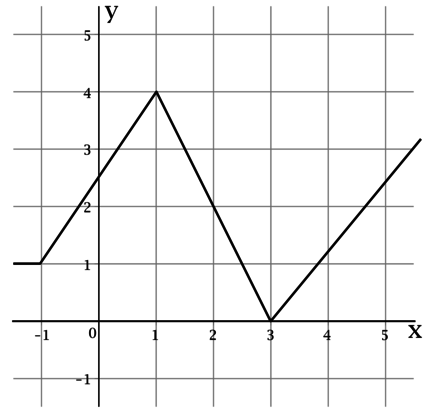
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой на
интервале Пользуясь рисунком, определите количество решений уравнения
на отрезке
Показать ответ и решение
Так как — одна из первообразных функции
то
Производная равна нулю в точках, в которых касательная к графику функции
расположена горизонтально.
Таких точек на отрезке ровно 6.
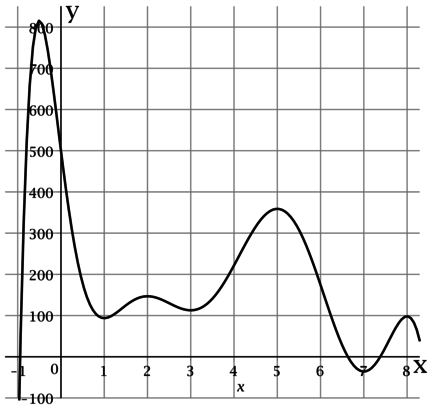
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой
на интервале Определите по рисунку количество решений уравнения
на отрезке
Показать ответ и решение
По определению первообразной Тогда имеем:
Отсюда получаем
Показать ответ и решение
По определению первообразной Тогда имеем:
Отсюда получаем
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой
на интервале Определите по рисунку количество решений уравнения
на отрезке
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой
на интервале Определите по рисунку количество решений уравнения
на отрезке
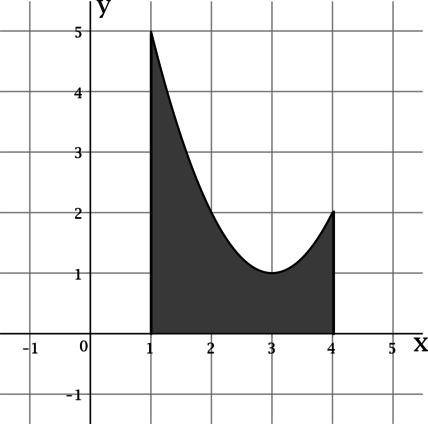
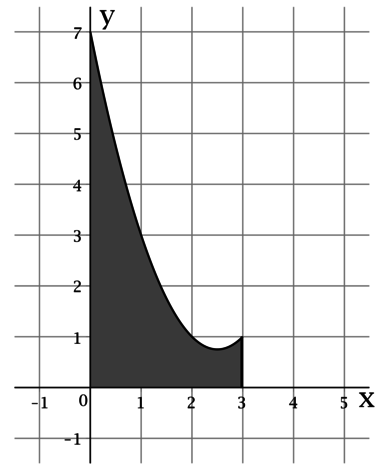
На рисунке изображён график некоторой функции Функция
— одна из первообразных
функции Найдите площадь закрашенной фигуры.
Показать ответ и решение
Нам нужно найти площади под графиком функции на отрезке
Такая площадь равна интегралу
По
формуле Ньютона-Лейбница имеем:
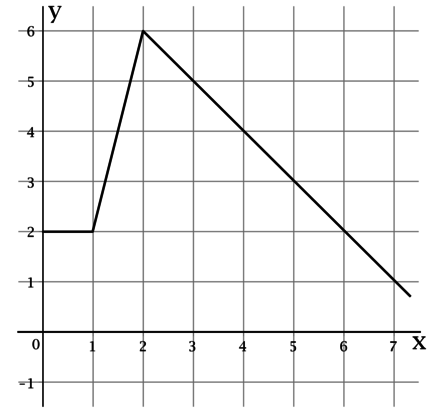
На рисунке изображён график функции Пользуясь рисунком, вычислите
где
— одна из
первообразных функции
Показать ответ и решение
По формуле Ньютона-Лейбница имеем:
Заметим, что такой интеграл равен площади под графиком функции на отрезке
Значит, нам
нужно найти площадь выделенной фигуры, состоящей из прямоугольного треугольника и двух прямоугольников:
Тогда имеем:
На рисунке изображён график функции Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
На рисунке изображён график функции Вычислите по рисунку
где
— одна из первообразных
функции
На рисунке изображён график функции Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
На рисунке изображён график функции Вычислите по рисунку
где
— одна из первообразных
функции
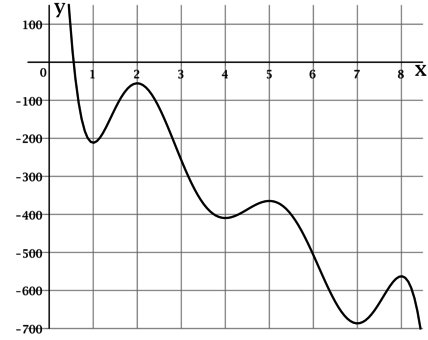
На рисунке изображён график функции — одной из первообразных
функции определённой на интервале
Найдите количество решений
уравнения на отрезке
Показать ответ и решение
По определение первообразной то есть решением уравнения
будут точки экстремума функции
которые помечены на графике.
Получим семь точек.
| Урок 1 | Геометрический смысл производной | – |
|---|---|---|
| Задание 1 | Справочный материал: геометрический смысл производной | |
| Задание 2 | Прямая y = 7x – 5 параллельна касательной к графику функции. Найти абсциссу точки касания – Предварительный просмотр | |
| Задание 3 | Прямая ?=−4?−11 является касательной к графику квадратичной функции. Найти абсциссу точки касания | |
| Задание 4 | Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней. | |
| Задание 5 | На рисунке изображен график производной функции . Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = – 2x – 11 или совпадает с ней. | |
| Задание 6 | Как найти значение производной в данной точке, если к графику функции проведена касательная | |
| Задание 7 | Найдите значение производной функции в точке ?_0=8. | |
| Задание 8 | На рисунке изображен график производной функции f(x) | |
| Урок 2 | Признаки возрастания и убывания функции. Точки экстремума. | – |
| Задание 1 | Справочный материал: признаки возрастания и убывания функции, точки экстремума | |
| Задание 2 | В какой точке отрезка функция принимает наибольшее значение | |
| Задание 3 | В какой точке отрезка функция принимает наименьшее значение | |
| Задание 4 | Найдите сумму точек экстремума | |
| Задание 5 | Найти количество точек максимума функции по графику производной | |
| Задание 6 | Найти сумму целых целых точек на промежутках возрастания функции по графику производной | |
| Задание 7 | Найти длину наибольшего промежутка возрастания функции | |
| Задание 8 | Определите количество целых точек, в которых производная функции положительна. | |
| Задание 9 | Определите количество целых точек, в которых производная функции f(x) отрицательна. | |
| Задание 10 | Найти количество точек минимума функции по графику производной | |
| Задание 11 | Найти количество точек максимума функции по графику производной | |
| Задание 12 | По графику производной найти точку экстремума функции | |
| Задание 13 | По графику производной найти количество точек экстремума | |
| Задание 14 | В скольких точках производная функции отрицательна? | |
| Задание 15 | В скольких точках производная функции положительна? | |
| Задание 16 | По графику производной определить, в скольких точках функция возрастает | |
| Задание 17 | По графику производной определить, в скольких точках функция убывает | |
| Задание 18 | Определить по графику функции, в какой точке значение производной наибольшее | |
| Задание 19 | Определить по графику функции, в какой точке значение производной наименьшее | |
| Урок 3 | Физический смысл производной | – |
| Задание 1 | Физический смысл производной | |
| Задание 2 | По уравнению координаты найти скорость точки | |
| Задание 3 | По уравнению координаты найти время движения точки | |
| Задание 4 | Сколько раз скорость точки обращалась в ноль | |
| Урок 4 | Первообразная | – |
| Задание 1 | По графику y=F(x) найти количество решений уравнения f(x)=0 | |
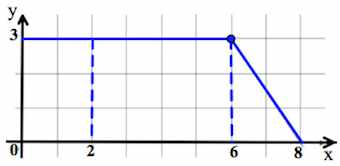
| Задание 2 | Пользуясь рисунком, вычислите F(8)-F(2) | |
| Задание 3 | По графику функции найти площадь закрашенной фигуры. |
10
Авг 2013
Категория: 07 Производная, ПО
07. Первообразная
2013-08-10
2022-09-11
Задача 1. На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите
, где
— одна из первообразных функции
.
Решение: + показать
Задача 2. На рисунке изображён график некоторой функции . Функция
— одна из первообразных функции
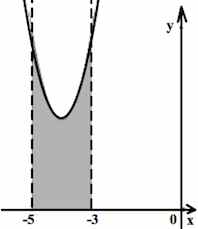
. Найдите площадь закрашенной фигуры.
Решение: + показать
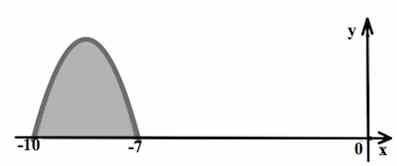
Задача 3. На рисунке изображён график некоторой функции . Функция
— одна из первообразных функции
. Найдите площадь закрашенной фигуры.
Решение: + показать
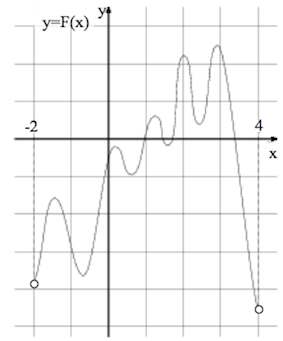
Задача 4. На рисунке изображён график функции – одной из первообразных некоторой функции
, определённой на интервале
. Пользуясь рисунком, определите количество решений уравнения
на отрезке
.
Решение: + показать

Вы можете пройти тест «Первообразная»
Автор: egeMax |
комментариев 7
Решение:
Площадь под графиком функции f(x) на отрезке [a; b] равна разности первообразных:
S = F(b) – F(a)
Нам необходимо найти площадь закрашенной фигуры на отрезке [-8; -6], то есть a = -8; b = -6. Значит S = F(-6) – F(-8).
Найдем F(-8):
F(-8) = (-8)3 + 21⋅(-8)2 +151⋅(-8) – 1
F(-8) = – 512 + 21⋅64 – 151⋅8 – 1
F(-8) = – 512 + 1344 – 1208 – 1
F(-8) = – 513 + 136
F(-8) = -377
Найдем F(-6):
F(-6) = (-6)3 + 21⋅(-6)2 +151⋅(-6) – 1
F(-6) = – 216 + 21⋅36 – 151⋅6 – 1
F(-6) = – 216 + 756 – 906 – 1
F(-6) = – 217 – 150
F(-6) = -367
Тогда площадь закрашенной фигуры равна:
S = F(-6) – F(-8) = -367 – (-377) = -367 + 377 = 10
Ответ: 10