Найдите площадь закрашенной фигуры на координатной плоскости (см. рис.).
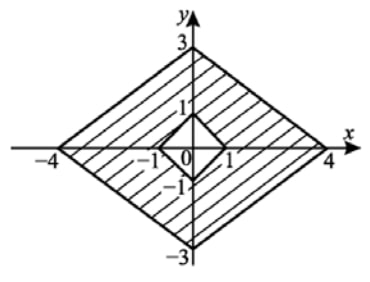
Решение:
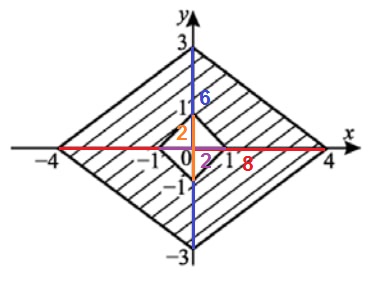
Найдём площадь большего ромба с диагоналями 6 и 8:
S_{1}=frac{1}{2}cdot d_{1}cdot d_{2}=frac{1}{2}cdot 6cdot 8=24
Найдём площадь меньшего ромба с диагоналями 2 и 2:
S_{2}=frac{1}{2}cdot d_{1}cdot d_{2}=frac{1}{2}cdot 2cdot 2=2
Найдём площадь закрашенной фигуры:
S = S1 – S2 = 24 – 2 = 22
Ответ: 22.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 15228 Найдите площадь закрашенной фигуры на…
Условие
![]()
slava191
22.04.2017
Найдите площадь закрашенной фигуры на координатной плоскости.
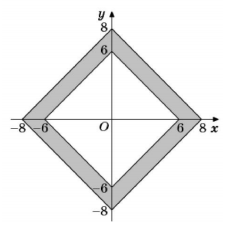
математика 10-11 класс
3862
Решение
![]()
MargaritaPyrkina
22.04.2017
★
S(закраш)=S(внешнего ромба)-S(внутреннего ромба)
S(внешнего ромба)=0,5*16*16=128 (половина произведения диагоналей)
S(внутреннего ромба)=0,5*12*12=72
S(закраш)=128-72=56
Ответ: 56
Ошибки в решение (1)
Написать комментарий
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач
Присоединяйся в ВК
16-9=7 разность площадей первого и второго ромба (первый закрашенный участок)
4-1=3 разность площадей третьего и четвертого ромба (второй закрашенный участок)
7+3=10 сумма площадей двух закрашенных участков — площадь закрашенной фигуры
Отмена
Вячеслав Хаммадиев
Отвечено 30 сентября 2019
-
Комментариев (0)
Добавить
Отмена
Найдите площадь закрашенной фигуры на координатной плоскости
- Категория: Задачи по планиметрии
Найдите площадь закрашенной фигуры на координатной плоскости.
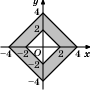
Решение:
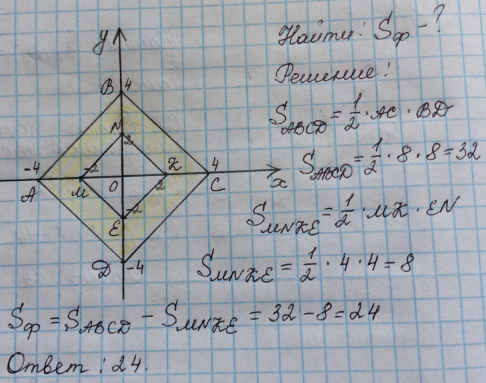
Ответ: 24.
