Как найти площадь закрашенной фигуры треугольника - Сайт, где вы сможете решить свои вопросы

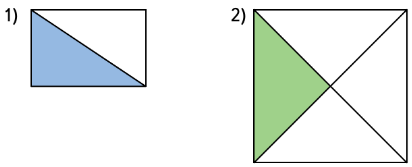
Найди способ вычисления площади закрашенного треугольника. Выполни вычисления.

reshalka.com

ГДЗ учебник по математике 3 класс (часть 1) Рудницкая. Произведение трех и более множителей. Номер №27

Решение

Задание выполняется по следующему плану.
1) Измеряем длины сторон прямоугольника и квадрата.
2) Вычисляем площадь каждой фигуры.
3) Значение площади прямоугольника делим пополам, а значение площади квадрата делим на 4.

Решение:
1) 3 * 2 =
6

− площадь всего прямоугольника.
2) 6 : 2 =
3

− площадь закрашенного треугольника.
Ответ:
3

Решение:
1) 4 * 4 =
16

− площадь всего квадрата.
2) 16 : 4 =
4

− площадь закрашенного треугольника.
Ответ:
4

Источник

В едином государственном экзамене по математике в части B есть задача, где нужно вычислить площадь закрашенной фигуры. Несмотря на свою простоту, в этой задаче часто допускают ошибки. В этой статье вы узнаете, как решить задачу части В, зная всего лишь одну формулу (площадь прямоугольного треугольника равна половине произведения катетов).

Пример 1

Простейшая задача ЕГЭ, которую многие не могут решить

Площадь красного квадрата = 6 х 6 = 36.

Площадь фигуры 1 = (6 х 1) / 2 = 3.

Площадь фигуры 2 = (4 х 1) / 2 = 2

Площадь фигуры 3 = 1 х 1 = 1

Площадь фигуры 4 = (3 х 1) / 2 = 1,5

Площадь фигуры 5 = (2 х 6) / 2 = 6

Площадь закрашенной фигуры = 36 – (3 + 2 + 1 + 1,5 + 6) = 36 – 13,5 = 22,5

Пример 2

Площадь закрашенного треугольника в прямоугольнике 1 = (6 х 4) / 2 = 12

Площадь закрашенного треугольника в прямоугольнике 2 = (6 х 2) / 2 = 6

Площадь закрашенной фигуры = 12 + 6 = 18

Пример 3

Площадь красного прямоугольника = (7 – 3) х (9 – 1) = 4 х 8 = 32

Площадь фигуры 1 = (7 – 3) х (3 -1) / 2 = 4 х 2 / 2 = 4

Площадь фигуры 3 = (7 – 3) х (9 – 5) / 2 = 4 х 4 / 2 = 8

Площадь закрашенной фигуры (фигуры 2) = 32 – 4 – 8 = 20

Пример 4

Площадь закрашенной фигуры = (10 – 4) х (9 -1) = 6 х 8 = 48

Пример 5

Диагональ большого квадрата = 16

Диагональ малого (внутреннего) квадрата = 8

Площадь большого квадрата = 1 / 2 * 16² = 1/2 * 256 = 128

Площадь малого квадрата = 1 / 2 * 8² = 1/2 * 64 = 32

Площадь закрашенной фигуры = 128 – 32 = 96

Если забыли как найти площадь квадрата, зная диагональ, то можно разложить эту фигуру на прямые треугольники и вычислить площадь, как в примерах выше.

Понравилась статья? Ставь лайк и подписывайся на Математику. Впереди много интересного.

Источник

Подскажите пожалуйста ” Как найти площадь закрашенного треугольника” (Фото есть)

Знаток

(488),
закрыт

11 лет назад

Светлана Носова

Оракул

(75361)

11 лет назад

Общая площадь 4-х угольника 6*7=42.
Теперь вычислим площади 3-х угольников, кот. отсекают закрашенный.

1) 6*4/2=12
2)3*4/2=6
3)2*7/2=7
Сложим: 12+6+7=25
Узнаем площадь закрашенного 3-ка: 42-25=17 (квадратов).

Naumenko

Высший разум

(856099)

11 лет назад

посчитать клеточки – длины сторон 2-х соседних – прямоугольника и вычислить его площадь.
таким же образом найти длины катетов 3-х прямоугольных тр-ков и найти половину произведения их – это будут площади незакрашенных частей.

из площади всего прямоугольника вычесть площадь трех тр-ков – вот и ответ.

Сергей Нуждин

Просветленный

(43192)

11 лет назад

Выше даны точные ответы. А если надо приближённый – то алгоритм такой:
Считаем сумму всех целых квадратов внутри треугольника и добавляем половину суммы нецелых квадратов

Целых квадратов 8
Нецелых 18

Итого 8+18/2=17 квадратов

Что совпадает с ответом Светланы ))

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Все категории

Фотография и видеосъемка
Знания
Другое
Гороскопы, магия, гадания
Общество и политика
Образование
Путешествия и туризм
Искусство и культура
Города и страны
Строительство и ремонт
Работа и карьера
Спорт
Стиль и красота
Юридическая консультация
Компьютеры и интернет
Товары и услуги
Темы для взрослых
Семья и дом
Животные и растения
Еда и кулинария
Здоровье и медицина
Авто и мото
Бизнес и финансы
Философия, непознанное
Досуг и развлечения
Знакомства, любовь, отношения
Наука и техника

Найди способ вычисления площади закрашенного треугольника, выполни вычисления,
1) Длина – 3см, ширина – 2см. Треугольник закрашен половину квадрата. 2) Квадрат – длина 4см, ширина 4см. Квадрат поделен на 4 части прямоугольника. Нужно найти 1 его часть закрашенную.

1 ответ:

0

0

1) S=ab (площадь прямоугольника равна длина умноженная на ширину)
    3×2=6 (см²) – площадь прямоугольника
    6:2=3 (см²) – площадь треугольника
2) 4×4=16 (см²) – площадь квадрата
   16:4 = 4 (см²) – площадь закрашенной части ( 1/4 квадрата)

ГДЗ учебник по математике 3 класс (часть 1) Рудницкая. Произведение трех и более множителей. Номер №27

Решение

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Понравилась статья? Ставь лайк и подписывайся на Математику. Впереди много интересного.

Подскажите пожалуйста ” Как найти площадь закрашенного треугольника” (Фото есть)

Вам также может понравиться

Как найти марсианскую руду

Как найти жену без детей

Как найти баланс лыжи

Добавить комментарий Отменить ответ