Как найти площадь замкнутой фигуры

Вычислить площадь фигуры, ограниченной линиями

Вычислить
площадь фигуры, ограниченной линиями .

Решение.

Находим
точки пересечения заданных линий. Для
этого решаем систему уравнений:

Для
нахождения абсцисс точек пересечения
заданных линий решаем уравнение:

   
или
   .

Находим: x₁ =
-2, x₂ =
4.

Итак,
данные линии, представляющие собой
параболу и прямую, пересекаются в
точках A(-2;
0), B(4;
6).

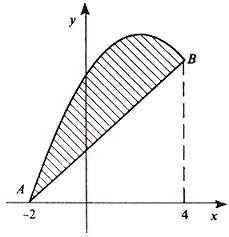
Эти
линии образуют замкнутую фигуру, площадь
которой вычисляем по указанной выше
формуле:

По
формуле Ньютона-Лейбница находим:

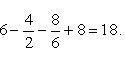
Найти
площадь области, ограниченной эллипсом .

Решение.

Из
уравнения эллипса для I
квадранта имеем .
Отсюда
по формуле  получаем

Применим
подстановку x = a sin t, dx = a cos t
dt.
Новые пределы интегрирования t = α и t = β определяются
из уравнений 0 = a sin t, a = a sin t.
Можно положить α =
0 и β = π/2.

Находим
одну четвертую искомой площади

Отсюда S = πab.

Найти
площадь фигуры, ограниченной линиями y =
–x² + x +
4 и y =
–x +
1.

Решение.

Найдем
точки пересечения линий y =
–x² + x +
4, y =
–x +
1, приравнивая ординаты линий: –x² + x +
4 = –x +
1 или x² –
2x –
3 = 0. Находим корни x₁ =
-1, x₂ =
3 и соответствующие им ординаты y₁ =
2, y₂ =
-2.

По
формуле площади фигуры получаем

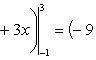
Определить
площадь, ограниченную параболой y = x² +
1 и прямой x + y =
3.

Решение.

Решая
систему уравнений

находим
абсциссы точек пересечения x₁ =
-2 и x₂ =
1.

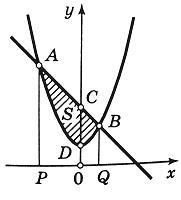
Полагая y₂ =
3 – x и y₁ = x² +
1, на основании формулы  получаем

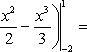
Вычислить
площадь, заключенную внутри лемнискаты
Бернулли r² = a²cos
2φ.

Решение.

В
полярной системе координат площадь
фигуры, ограниченной дугой кривой r = f(φ)
и двумя полярными радиусами φ₁ = ʅ и φ₂ = ʆ,
выразится интегралом

В
силу симметрии кривой определяем сначала
одну четвертую искомой площади

Следовательно,
вся площадь равна S = a².

Вычислить
длину дуги астроиды x^2/3 + y^2/3 = a^2/3.

Решение.

Запишем
уравнение астроиды в виде

(x^1/3)² +
(y^1/3)² =
(a^1/3)².

Положим x^1/3 = a^1/3cos t, y^1/3 = a^1/3sin t.

Отсюда
получаем параметрические уравнения
астроиды

x = a cos³t,     y = a sin³t,     (*)

где
0 ≤ t ≤
2π.

Ввиду
симметрии кривой (*) достаточно найти
одну четвертую часть длины дуги L,
соответствующую изменению параметра t от
0 до π/2.

Получаем

dx =
-3a cos²t sin t
dt,     dy =
3a sin²t cos t
dt.

Отсюда
находим

Интегрируя
полученное выражение в пределах от 0
до π/2,
получаем

Отсюда L =
6a.

Найти
площадь, ограниченную спиралью
Архимеда r = aφ и
двумя радиусами-векторами, которые
соответствуют полярным углам φ₁и φ₂ (φ₁ < φ₂).

Решение.

Площадь,
ограниченная кривой r = f(φ)
вычисляется по формуле ,
где α и β –
пределы изменения полярного угла.

Таким
образом, получаем

     (*)

Из
(*) следует, что площадь, ограниченная
полярной осью и первым витком спирали
Архимеда (φ₁ =
0; φ₂ =
2π):

Аналогичным
образом находим площадь, ограниченную
полярной осью и вторым витком спирали
Архимеда (φ₁ =
2π; φ₂ =
4π):

Искомая
площадь равна разности этих площадей

Вычислить
объем тела, полученного вращением вокруг
оси Ox фигуры,
ограниченной параболами y = x² и x = y².

Решение.

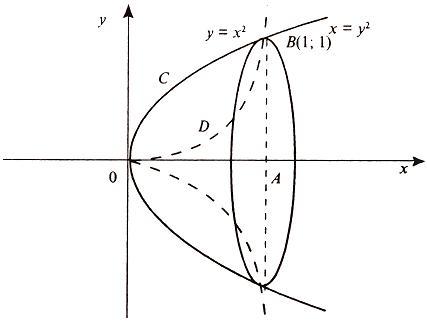
Решим
систему уравнений

и
получим x₁ =
0, x₂ =
1, y₁ =
0, y₂ =
1, откуда точки пересечения кривых O(0;
0), B(1;
1). Как видно на рисунке, искомый объем
тела вращения равен разности двух
объемов, образованных вращением вокруг
оси Ox криволинейных
трапеций OCBA и ODBA:

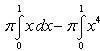
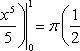
Вычислить
площадь, ограниченную осью Ox и
синусоидой y =
sin x на
отрезках: а) [0, π];
б) [0, 2π].

Решение.

а)
На отрезке [0, π]
функция sin x сохраняет
знак, и поэтому по формуле ,
полагая y =
sin x,
находим

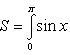
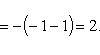
б)
На отрезке [0, 2π],
функция sin x меняет
знак. Для корректного решения задачи,
необходимо отрезок [0, 2π]
разделить на два [0, π]
и [π,
2π],
в каждом из которых функция сохраняет
знак.

По
правилу знаков, на отрезке [π,
2π]
площадь берется со знаком минус.

В
итоге, искомая площадь равна

Определить
объем тела, ограниченного поверхностью,
полученной от вращения эллипса  вокруг
большой оси a.

Решение.

Учитывая,
что эллипс симметричен относительно
осей координат, то достаточно найти
объем, образованный вращением вокруг
оси Oxплощади OAB,
равной одной четверти площади эллипса,
и полученный результат удвоить.

Обозначим
объем тела вращения через V_x;
тогда на основании формулы  имеем ,
где 0 и a –
абсциссы точек B и A.
Из уравнения эллипса находим .
Отсюда

Таким
образом, искомый объем равен .
(При вращении эллипса вокруг малой
оси b,
объем тела равен )

Найти
площадь, ограниченную параболами y² =
2px и x² =
2py.

Решение.

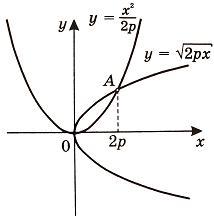
Сначала
найдем координаты точек пересечения
парабол, чтобы определить отрезок
интегрирования. Преобразуя исходные
уравнения, получаем  и .
Приравнивая эти значения, получим  или x⁴ –
8p³x =
0.

Отсюда

x⁴ –
8p³x = x(x³ –
8p³)
= x(x –
2p)(x² +
2px +
4p²)
= 0.

Находим
корни уравнений:

Учитывая
то факт, что точка A пересечения
парабол находится в первой четверти,
то пределы интегрирования x =
0 и x =
2p.

Искомую
площадь находим по формуле

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.

Определение.

Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).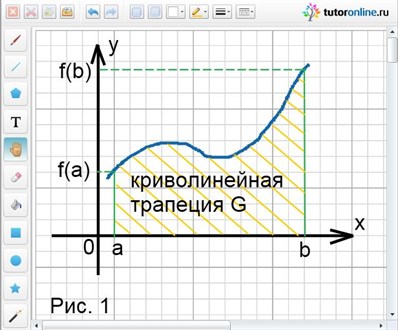

Определенный интеграл ʃ_а^b f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.

То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл  ʃ_а^b f(x)dx.

Таким образом, S(G) = ʃ_а^b f(x)dx.

В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃ_а^b f(x)dx.

Пример 1.

Вычислить площадь фигуры, ограниченной линиями у = х³; у = 1; х = 2.

Решение.

Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.

Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.

Используя формулу S = ʃ_а^b f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:

{у = х³,
{у = 1.

Таким образом, имеем х₁ = 1 – нижний предел и х = 2 – верхний предел.

Итак, S = S_DACE – S_DABE = ʃ₁² x³ dx – 1 = x⁴/4|₁² – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).

Ответ: 11/4 кв. ед.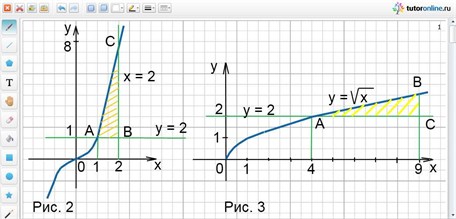

Пример 2.

Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.

Решение.

Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции

у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.

Искомая площадь равна S = ʃ_а^b(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:

{у = √х,
{у = 2.

Таким образом, имеем, что х = 4 = а – это нижний предел.

Итак, S = ∫₄⁹ (√x – 2)dx = ∫₄⁹ √x dx –∫₄⁹ 2dx = 2/3 x√х|₄⁹ – 2х|₄⁹ = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).

Ответ: S = 2 2/3 кв. ед.

Пример 3.

Вычислить площадь фигуры, ограниченной линиями у = х³ – 4х; у = 0; х ≥ 0.

Решение.

Построим график функции у = х³ – 4х при х ≥ 0. Для этого найдем производную у’:

y’ = 3x² – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.

Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции у_min = -16/(3√3) ≈ -3.

Определим точки пересечения графика с осями координат:

если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;

если у = 0, то х³ – 4х = 0 или х(х² – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х₁ = 0, х₂ = 2, х₃ = -2 (не подходит, т.к. х ≥ 0).

Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.

Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.

Так как функция у = х³ – 4х принимает на (0; 2) отрицательное значение, то

S = |ʃ₀² (x³ – 4x)dx|.

Имеем: ʃ₀² (x³ – 4х)dx =(x⁴/4 – 4х²/2)|₀²= -4, откуда S = 4 кв. ед.

Ответ: S = 4 кв. ед.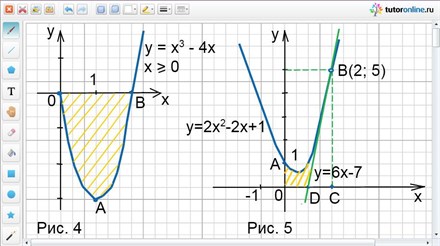

Пример 4.

Найти площадь фигуры, ограниченной параболой у = 2х² – 2х + 1, прямыми  х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х₀ = 2.

Решение.

Сначала составим уравнение касательной к параболе у = 2х² – 2х + 1 в точке с абсциссой х₀ = 2.

Так как производная y’ = 4x – 2, то при х₀ = 2 получим k = y’(2) = 6.

Найдем ординату точки касания: у₀ = 2 · 2² – 2 · 2 + 1 = 5.

Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.

Построим фигуру, ограниченную линиями:

у = 2х² – 2х + 1, у = 0, х = 0, у = 6х – 7.

Г_у =  2х² – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение  2х² – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:

x_b = -b/2a;

x_b = 2/4 = 1/2;

y_b = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).

Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.

Имеем: S_ОAВD = S_OABC – S_ADBC.

Найдем координаты точки D из условия:

6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.

Площадь треугольника DBC найдем по формуле S_ADBC = 1/2 · DC · BC. Таким образом,

S_ADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.

Далее:

S_OABC = ʃ₀²(2x² – 2х + 1)dx = (2x³/3 – 2х²/2 + х)|₀² = 10/3 (кв. ед.).

Окончательно получим: S_ОAВD = S_OABC – S_ADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).

Ответ: S = 1 1/4 кв. ед.

Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.



Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:

Пример 10
Вычислить площадь фигуры, ограниченной линиями .

И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.

В нашей задаче: прямая  определяет ось , прямые  параллельны оси  и парабола  симметрична относительно оси , для неё находим несколько опорных точек:

Искомую фигуру желательно штриховать:

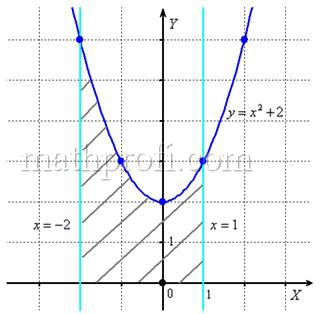
Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке   график функции  расположен над осью , поэтому искомая площадь:

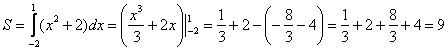
Ответ:

После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.

И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.

Пример 11
Вычислить площадь фигуры, ограниченной линиями  и осью

Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :

Пример 12
Вычислить площадь фигуры, ограниченной линиями ,  и координатными осями.

Решение: найдём несколько опорных точек для построения экспоненты:

и выполним чертёж, получая фигуру площадью около двух клеток:

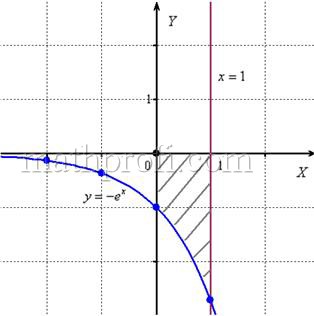
Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле: .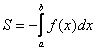
В данном случае: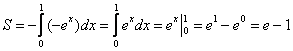

Ответ:  – ну что же, очень и очень похоже на правду.

На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:

Пример 13
Найти площадь плоской фигуры, ограниченной линиями , .

Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы  и прямой , поскольку здесь будут находиться пределы интегрирования.  Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:

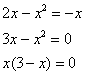
таким образом:

Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».

С прямой  всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
 – именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:

Выполним чертеж:

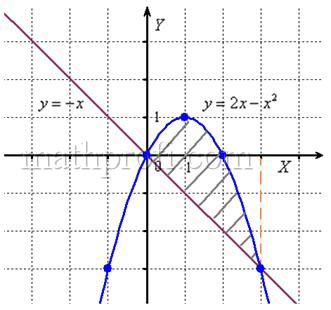
А теперь рабочая формула: если на отрезке  некоторая непрерывная функция  больше либо равна непрерывной функции , то площадь фигуры, ограниченной графиками этих функций и отрезками прямых , можно найти по формуле:

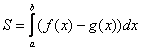
Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.

В нашем примере очевидно, что на отрезке  парабола располагается выше прямой, а поэтому из  нужно вычесть

Завершение решения может выглядеть так:

На отрезке : , по соответствующей формуле:

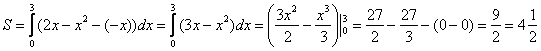
Ответ:

Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 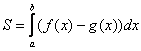. Поскольку ось  задаётся уравнением , то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу 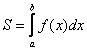 либо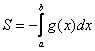

А сейчас пара типовых задач для самостоятельного решения

Пример 14
Найти площадь фигур, ограниченных линиями:

а) , .

б) , ,

Решение с чертежами и краткими комментариями в конце книги

В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:

Пример 15
Вычислить площадь фигуры, ограниченной линиями

Решение: выполним бесхитростный чертёж,

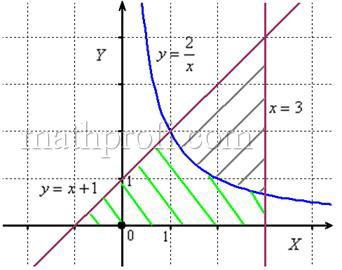
хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую  можно недочертить до оси , и тогда мы вовсе не увидим нужную фигуру.

Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:

1) на отрезке  над осью  расположен график прямой ;
2) на отрезке  над осью  расположен график гиперболы .

Совершенно понятно, что площади можно (и нужно) сложить:

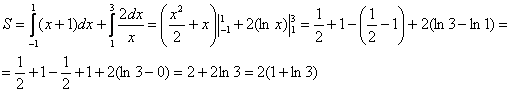
Ответ:

И познавательный пример для самостоятельного решения:

Пример 16
Вычислить площадь фигуры, ограниченной линиями , ,  и координатными осями.

Итак, систематизируем важные моменты этой задачи:

На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс  зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.

Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.

Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой  и прямой , где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:

и находим его корни:
 – нижний предел интегрирования,  – верхний предел.

Во-вторых, не всегда понятен «внешний вид» линии, и функция  (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html

После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.

Составляем определённый интеграл или несколько интегралов по формуле 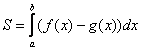, все основные вариации мы разобрали выше.

Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.

Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!

1.9. Объём тела вращения

1.7. Геометрический смысл определённого интеграла

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми и и графиком функции . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция неотрицательна на отрезке и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

где — площадь внутренней ступенчатой фигуры, —площадь внешней ступенчатой фигуры, и . С другой стороны, по определению интеграла можно записать:

Таким образом, числа и разделяют одни и те же числовые множества: . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции , сверху графиком функции , а слева и справа прямыми (рис. 30), то ее площадь выражается формулой

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами .

Пусть теперь функция непрерывна на отрезке и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке функции , которая на принимает только неотрицательные значения. По доказанному выше

. Но

Значит,

Как мы видим, в рассматриваемом случае интеграл дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке в конечном числе точек, то значение интеграла дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

---

Пример 1. Найти площадь фигуры, ограниченной кривой , осью абсцисс и прямыми (рис. 33).

Решение. Имеем: (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы и отрезком прямой (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

Пример 3. Найти площадь фигуры, ограниченной графиками функций (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника и прямоугольного треугольника

---

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Записав уравнение кривой в виде , найдем точки пересечения ее с осью , положив . Учитывая сказанное, найдем площадь половины петли:

Воспользовавшись формулой из таблицы при , получим:

Значит, окончательно имеем:

---

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая задана в параметрической форме

где функция монотонна на отрезке , причем , и имеет на этом отрезке непрерывную производную. Так как , то по формуле замены переменной под знаком определенного интеграла получаем:

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

---

Пример 5. Вычислить площадь эллипса, заданного параметрически

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке соответствует значение , а точке — значение . Поэтому

---

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами и , выходящими из точки , и непрерывной кривой (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть — полярное уравнение кривой , а и — углы между полярной осью и лучами и соответственно. При этом пусть функция непрерывна на .

Разобьем данный сектор на частей лучами

и рассмотрим k-й частичный сектор (рис. 39). Пусть — наименьшее значение функции в , a — наибольшее значение функции в этом отрезке.

Построим два круговых сектора с радиусами и . Обозначим через величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна , а площадь внешней фигуры равна — . Эти выражения являются нижней и верхней суммами Дарбу и для интеграла . Так как функция непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого найдется такое разбиение отрезка , что . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

В то же время по определению определенного интеграла

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

---

Пример 6. Вычислить площадь, ограниченную одним лепестком розы (рис. 40).

Решение. Значениям и соответствует Поэтому

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.