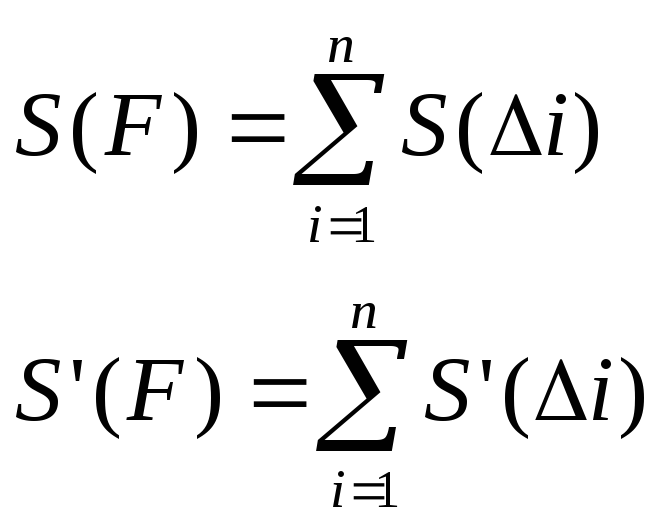Лек ция 16
Площадь
многоугольника в евклидовой геометрии.
Теоремы существования измерения площади
фигуры.
Теорема
единственности.
Определение
16.1. Ломаной
называется фигура, состоящая n-1
отрезков
–
звеньев ломаной.
Определение
16.2. Ломаная
называется простой, если смежные звенья
(А1А2
и А2А3,
А3А4
и А4А5)
не лежат на одной прямой и несмежные
звенья не имеют общих точек.
Определение
16.3. Ломаная
называется замкнутой, если ее концы
совпадают (.
Определение
16.4. Объединение
замкнутой ломаной и её внутренней
области называется многоугольником.
Замкнутая ломаная, ограничивающая
многоугольник, является его границей.
Определение
16.5. Многоугольник
называется ориентированным, если указан
порядок обхода его вершин, т.е.
.
Пусть
.
Введем на многоугольниках
ориентации
так, чтобы общие вершины
и
,
и
следовали друг за другом в одном и том
же порядке. В этом случае говорят, что
ориентации этих многоугольников
согласованы и
.
Пусть
–
евклидова плоскость, М
– множество всех многоугольников данной
плоскости,
–
единичный вектор, перпендикулярный
плоскости
,
и
– произвольные векторы, параллельные
плоскости
.
Смешанное
произведение
обозначим
.
Выберем на плоскости
ортонормированный базис
так, чтобы
.
Если в данном
базисе
Пусть
ориентированный n-угольник,
а точка О – произвольная точка
.
Определение
16.6. Число
,
где
и
называется характеристикой многоугольника
F.
Если в прямоугольной
системе координат
плоскости
вершины многоугольника
имеют координаты
где
i=
1,2…n,
то характеристику многоугольника можно
записать в виде:
()
Свойства
характеристики многоугольника
1). Характеристика
многоугольника
не зависит от выбора точки О на плоскости
;
2). Если
,
то
>
и
>
;
3). Если
– произвольный многоугольник, то
,
поэтому
>0
;
4). При замене
ориентации многоугольника характеристика
меняет знак на противоположный, но
абсолютная величина характеристики не
меняется.
5). Любой многоугольник
можно ориентировать так, чтобы его
характеристика была положительной.
Рассмотрим множество
М
всех многоугольников на евклидовой
плоскости. Говорят, что установлено
измерение площадей многоугольников
если определено отображение:
,
удовлетворяет следующим аксиомам:
1). Если
,то
;
2). Если
F=F1+F2,
то
S(F)=S(F1)+S(F2);
3). Если S(P0)=1.
где Р0
– квадрат, построенный на единичном
отрезке как на стороне.
Определение
16.7. Положительное
число S(F)
называется мерой или площадью
многоугольника F,
а квадрат P0–
единичный квадрат.
Теорема 16.8.
(теорема существования) Отображение
по закону
удовлетворяет аксиомам 1, 2, 3 измерения
площадей.
Доказательство:
-
Докажем, что если
F=F’,
то S(F)=
S(F’)
.
Так как F=F’,
то существует движение, которое
многоугольник
переводит в многоугольник
.
Данное движение может быть заданно
двумя ортонормированными реперами
и
.
Если
–
вершины многоугольника
в репере
,
то
–
вершины многоугольника
в репере
.
Поэтому по формуле ()
получаем
,
а значит, S(F)=
S(F’).
2) Докажем что если
F=F1+F2
, то S(F)=
S(F1)+
S(F2)
многоугольник.
Многоугольник F
ориентирован так, чтобы
>0.
Введем на F1
и F2
ориентации,
согласованные с ориентацией многоугольника
.
Тогда
.
Докажем, что
.
Пусть М0……Мк
– ломаная, которая разбивает многоугольник
F
на многоугольники F1
и F2,
а
– радиус–векторы вершин этой ломаной,
радиус-векторы
вершин многоугольника А1….Аn.
Сложив эти равенства
и учитывая второе свойство характеристики,
имеем
Так
как точка М0
– точка
отрезка А1Аn,
то
,
поэтому
.
Аналогично
.
Значит,
=
S(F)=
S(F1)+
S(F2)
3) Пусть
– квадрат, построенный на единичном
отрезке. В системе координат
его вершины имеют координаты О(0,0),
А1(1,0),
А2(0,1),
А3(1,1).
Высчитав
характеристику, имеем:
.
Для её доказательства
теоремы единственности необходимо
следующие теоремы.
Теорема 16.9.
Если
– отображение, удовлетворяющее аксиомам
1,2,3, то
,
где
– прямоугольник, стороны которые равны
и
.
Теорема 16.10.
Если
– отображение, удовлетворяющее аксиомам
1,2,3, то
,
где Р–
треугольник,
–
одна из его сторон, а
–
соответствующая высота.
Теорема 16.11.
(теорема
единственности площади)
Если выбран
единичный отрезок, то существует не
более одного отображения
удовлетворяющего аксиомам 1,2,3.
Доказательство:
(методом от противного).
1). Пусть существуют
два отображения
и
которые удовлетворяют аксиомам 1,2,3, при
одном и том же выборе единичного отрезка.
2). Возьмем
произвольный многоугольник F
и разложим
его на конечное множество треугольников:
.
По аксиоме 2 имеем:
при
.
Полученное равенство справедливо для
любого многоугольника, следовательно,
допущение неверно и , значит, отображения
.
Следствие16.11.1.
При любом способе разложения многоугольника
на конечное множество треугольников
сумма площадей этих треугольников одна
и та же.
Следствие 16.11.2.
Если вершины многоугольника А1…Аn
в прямоугольной
системе координат заданы своими
координатами, то
Определение
16.12. Два
многоугольника называются равновеликими,
если их площади равны.
Определение
16.13. Два
многоугольника называются равносоставленными,
если их можно разложить на одно и то же
число равных многоугольников.
Если 2 многоугольника
равносоставлены, то они и равновелики.
Соседние файлы в папке вопрос 13
- #
- #
Площадь многоугольника
На чтение 2 мин Просмотров 3.2к. Опубликовано 22 января, 2021
Одна из прикладных задач, которые решает геометрия — вычисление площадей многоугольников. Это необходимо строителям, земледельцам, конструкторам, летчикам, геологам. Даже в повседневной жизни знание формул, показывающих, как узнать площадь многоугольника, часто выручает при ремонте квартиры или дома.
Сначала определимся, что такое многоугольник, и что такое площадь. В геометрии многоугольником называют фигуру на плоскости, образованную замкнутой ломаной линией с количеством звеньев более 2-х. Это все известные и неизвестные нам фигуры, начиная от треугольника — квадрат, трапеция, ромб, шестиугольник, восьмиугольник и т.д. Готовые формулы, как найти площадь многоугольника созданы практически для каждой правильной фигуры с конечным количеством сторон. А вот что делать с неправильными?
Площади самых распространенных многоугольников можно найти по готовым формулам:
Правильным многоугольником называется фигура, у которой все стороны равны, а смежные углы одинаковые. Площадь — часть плоскости, в которой лежит фигура, заключенная между ее сторонами. Если многоугольник нарисован в тетради в клеточку, то площадь — это количество квадратиков внутри фигуры. За единицу площади принят квадратный метр (м2), или квадратный сантиметр (см2), в зависимости от размеров многоугольника.
- Квадратный метр — площадь квадрата со сторонами длиной в 1 м;
- Квадратный сантиметр — площадь квадрата со стороной 1 см.
- В одном м2 помещается 10000 см2;
- 1 см2 = 1 ∙ 10-4 см.
Площадь многоугольника не обязательно равна целому числу квадратных единиц. Если у вас получится площадь, например, 22, 3 см2, расстраиваться не нужно. Есть еще квадратные миллиметры и более мелкие единицы.
Универсальный способ вычисления площади правильного многоугольника
Чтобы не запоминать десятки готовых формул, можно выучить только одну — как найти площадь многоугольника через периметр. Способ этот простой и не требует большого объема вычислений. Для работы нужны только линейка и карандаш.
Площади многоугольников на координатной сетке
5 февраля 2011
Многоугольники на координатной сетке — это самые простые задачи B5. Существует сразу несколько методов решения таких задачи, в том числе универсальный, описанный ниже. Для начала определимся с терминологией:
Многоугольник — фигура на плоскости, ограниченная замкнутой ломаной.
Большинство многоугольников, встречающихся в ЕГЭ, являются выпуклыми, т.е. не имеют внутренних углов размером больше 180°, а все вершины многоугольника лежат в узлах координатной сетки. Кроме того, ломаная, ограничивающая многоугольник, не имеет самопересечений. Все это значительно упрощает задачу.
Для решения всех задач этого типа достаточно выполнить четыре простых шага:
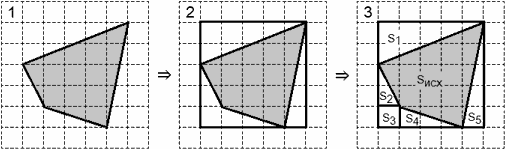
- Описать вокруг многоугольника прямоугольник, стороны которого параллельны осям координат (линиям сетки). При этом желательно, чтобы на каждой стороне прямоугольника присутствовала хотя бы одна вершина исходной фигуры;
- Разбить внутреннее пространство прямоугольника, не занятое исходной фигурой, на квадраты и треугольники. Лучше, если все линии разбиения будут параллельны осям координат;
- Найти площадь каждого элемента разбиения. Сложив эти площади, получим площадь всего разбиения;
- Наконец, из площади прямоугольника вычесть площадь разбиения — это и будет площадью исходной фигуры.
Несмотря на большое количество элементов разбиения, вычисление его площади — достаточно тривиальная задача.
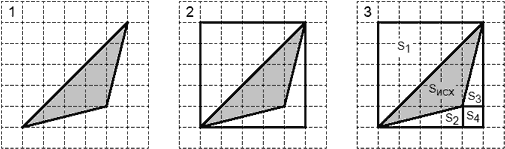
Проиллюстрируем каждый шаг решения:
Последним шагом найдем площадь исходной фигуры: Sисх = S − (S1 + S2 + S3 + S4 + S5), где S — площадь описанного прямоугольника. Осталось вычислить площадь большого прямоугольника и элементов разбиения. Эти несложные расчеты предлагается выполнить читателю в качестве упражнения.
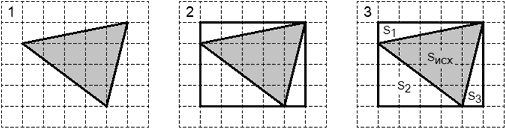
Задача. Найти площадь треугольника ABC, изображенного на рисунке:

Обозначение треугольника можно опустить, поскольку оно нам не потребуется. Приведем первые три шага:
Итак, Sисх = S − (S1 + S2 + S3), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения:
S1 = ½ · 1 · 5 = 2,5; S2 = ½ · 3 · 4 = 6; S3 = ½ · 1 · 4 = 2; S = 5 · 4 = 20.
Наконец, найдем площадь треугольника: Sисх = 20 − (2,5 + 6 + 2) = 9,5.
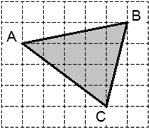
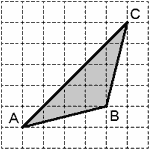
Задача. Найти площадь треугольника ABC, изображенного на рисунке:

Снова выполняем первые три шага. Заметим, что угол ABC — тупой, поэтому в разбиении присутствует квадрат. Имеем:
Очевидно, Sисх = S − (S1 + S2 + S3 + S4), где S — площадь описанного прямоугольника. Найдем площадь элементов разбиения:
S1 = ½ · 5 · 5 = 12,5; S2 = ½ · 4 · 1 = 2; S3 = ½ · 1 · 4 = 2; S4 = 1 · 1 = 1; S = 5 · 5 = 25.
Площадь треугольника: Sисх = 25 − (12,5 + 2 + 2 + 1) = 7,5.
Смотрите также:
- Задача B5: вычисление площади методом обводки
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- Системы линейных уравнений: основные понятия
- Тест к уроку «Знаки тригонометрических функций» (1 вариант)
- Координаты вершин правильного тетраэдра
- Задача B2 про комиссию в терминале