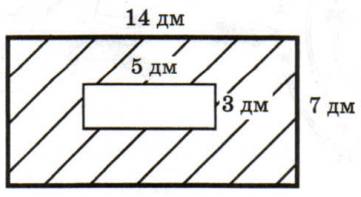
Найди площадь заштрихованной фигуры:

reshalka.com
ГДЗ учебник по математике 3 класс Петерсон. Часть 2. Урок 3. Номер №5
Решение
1) 14 * 7 = 98
(
д
м
2
)
− общая площадь большого прямоугольника;
×
14
7
¯
98
2) 5 * 3 = 15
(
д
м
2
)
− площадь маленького прямоугольника;
3) 98 − 15 = 83
(
д
м
2
)
− площадь заштрихованной фигуры.
Ответ: 83
д
м
2
Будучи школьником, когда ещё не было этих ваших интернетов, а я готовился к поступлению, мне позарез нужны были хорошие задачники и учебники, где всё коротко и по делу. И мало кто мог посоветовать что-то стоящее. Если у вас та же проблема, то рекомендую Галицкого по алгебре, Гордина по геометрии.
А ещё есть замечательный автор — Эдуард Николаевич Балаян. Он создал ни одну хорошую книгу для школьников. В том числе и для подготовки к олимпиадам. Полезно порешать и тем, кто претендует на 100 баллов по ЕГЭ. Причем начинать заниматься можно уже с 7 класса.
Сегодня хочу показать одну из последних задач для 9 класса из его книги “Геометрия. Задачи на готовых чертежах для подготовки к ГИА и ЕГЭ” (для 7-9 классов). Нам нужно найти площадь заштрихованной фигуры. Все данные на рисунке.
Всё, что у нас есть — равносторонний треугольник со стороной 15. Найти надо площадь заштрихованного трёхлистника.
Почти никто из девятиклассников эту задачу не решил за отведенное время. В школьных учебниках такие редко встречаются. А задача интересная и в приницпе несложная, надо только немного подумать, что-то достроить и все решится почти само. Сложных формул здесь нет.
Для тех, кто уже всё решил, вот ответ для сверки: S=75•(π-1,5√3)=112,5√3. Тех, кто не понимает, как получился этот ответ, приглашаю читать дальше.
Решение
Раз у нас равносторонний треугольник, понятно, что дуги окружностей одинаковые и наш трехлистник полностью симметричен относительно любой из высот треугольника. А ещё вспоминаем о том, что высоты в треугольнике пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины. Эта точка, к слову, является точкой пересечения всех трех дуг и по совместительству центром описанной возле треугольника окружности. Добавьте к этому формулу площади круга S=π•R² и получите всё, что нужно знать для решения этой задачи.
Пусть сторона правильного треугольника а=15. Тогда радиус окружности, описанной вокруг треугольника равен R=a/√3, а её площадь равна Sокр=π•a²/3. А площадь самого треугольника (эта формула дается в школе как самостоятельная, но её несложно вывести) равна S▲=(a²•√3)/4.
Теперь самое время заметить, что круг состоит из треугольника и трех жёлтых фрагментов за его пределами. Sокр=S▲+Sж, откуда Sж=Sокр-S▲.
Но если мы раскрасим три эти фрагмента в разные цвета и “загнем” внутрь треугольника, обнаружится, что их площадь в сумме (Sж) дает площадь треугольника (S▲) плюс площадь искомого трехлистника (S). Sж=S▲+S. Откуда искомая площадь S=Sж-S▲.
Учитывая ранее выведенное равенство Sж=Sокр-S▲, получаем, что искомая площадь находится через площадь описанной окружности и площадь треугольника S=Sокр-2•S▲=π•a²/3 – (a²•√3)/2 = π•15²/3 – 15²√3/2 = 15²/6•(2π-3√3) = 37,5•(2π-3√3) = 70•(π-1,5√3) = 112,5√3.
Как вам задача? Если понравилась, то, где найти похожие, вы знаете. Можете не благодарить, поставьте лайк, подпишитесь на канал и велком на мои каналы в Ютубе, Инстаграме и ТикТоке.
Ещё интересно: Где искать репетитора ребенку и как развить у него логику и нестандартное мышление
Задача про яблоки, которая вынесла почти всех
Легендарная задача, которая сбила с толку половину моих одноклассников и до сих путает учеников и родителей
Для начала добавим точки G и H на чертёж, чтобы потом было проще объяснить процесс решения:

Теперь площадь закрашенной фигуры AGCE можно найти, как разность площади целого прямоугольника ABCD и площадей трёх фигур, которые остались не закрашенными, а именно прямоугольной трапеции ABHG, прямоугольного треугольника CGH и прямоугольного треугольника CDE ( впрочем, возможны и другие варианты трапеций и треугольников ).
Площадь прямоугольника ABCD равна произведению длин его сторон:
S(ABCD) = AB * AD = ( AF + BF ) * ( AE + DE ) =
= ( 3 + 2 ) * ( 2 + 2 ) = 5 * 4 = 20 см²
Площадь прямоугольной трапеции ABHG равна половине произведения суммы длин её оснований и её же высоты:
S(ABHG) = ( AB + GH ) * BH / 2 =
= ( AF + FB + FB ) * AE / 2 =
= ( 3 + 2 + 2 ) * 2 / 2 = 7 см²
Площадь прямоугольного треугольника CGH равна половине произведения его катетов CH и GH:
S(CGH) = CH * GH / 2 =
= ED * FB / 2 = 2 * 2 / 2 = 2 см²
Площадь прямоугольного треугольника CDE равна половине произведения его катетов ED и CD:
S(CDE) = ED * DC / 2 =
= ED * ( AF + FB ) / 2 =
= 2 * ( 3 + 2 ) / 2 = 5 см²
Ну, и наконец можно найти площадь закрашенной фигуры AGCE:
S(AGCE) = S(ABCD) – S(ABHG) -S(CGH) – S(CDE) =
= 20 – 7 – 2 – 5 = 6 см²
Ответ: площадь закрашенной фигуры равна В) 6 см²
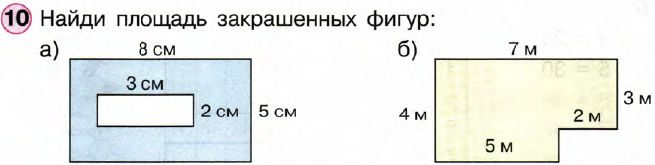
Нам нужно найти площадь закрашенных фигур, но мы умеем находить площадь только прямоугольника.
Поэтому, надо что-то придумать, т.е. как-то упростить это задание.
Как же поступить? На самом деле – все просто!
А) даны 2 прямоугольника: один большой — голубой, другой маленький – белый.
Причем маленький наложили на большой.
Если представим – на что похоже – на стену с окошком.
Надо найти площадь стены без окошка.
Итак:
1) сначала найдем площадь большого (голубого) прямоугольника, который был сначала, т.е. площадь стены:
8 х 5 = 40 (см2)
2) найдем площадь «окошка»:
3 х 2 = 6 (см2)
3) теперь из стены «вырежем» окошко:
40 – 6 = 36 (см2)
Т.о. площадь стены без окошка – это и есть площадь закрашенной фигуры.
Ответ: площадь закрашенной фигуры 36 см2.
Б) дан шестиугольник, его площадь мы найти сразу не можем.
Это задание можно выполнить разными способами.
1 способ.
1) Дорисуем наш шестиугольник до прямоугольника.
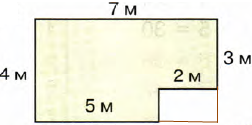
Найдем площадь полученного прямоугольника:
4 х 7 = 28 (м2)
2) теперь найдем площадь дорисованного прямоугольника:
Длина дорисованного – 2 см, ширину можем найти:
а) 4 – 3 = 1 (м)
б) находим площадь:
2 х 1 = 2 (м2)
3) чтобы найти первоначальную фигуру, надо от нового отрезать пририсованный, значит:
28 – 2 = 26 (м2) площадь шестиугольника.
2 способ.
Мы умеем находить площадь прямоугольника, поэтому разделим наш шестиугольник на прямоугольники – их будет два: левый и правый.
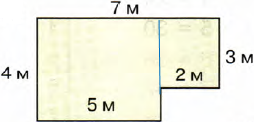
1) найдем площадь левого прямоугольника:
5 х 4 = 20 (м2)
2) находим площадь правого прямоугольника:
2 х 3 = 6 (м2)
3) находим площадь шестиугольника:
20 + 6 = 26 (м2)
3 способ.
Разделим наш шестиугольник на прямоугольники по-другому – их будет два: верхний и нижний.
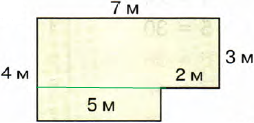
1) найдем площадь верхнего прямоугольника:
3 х 7 = 21 (м2)
2) находим площадь нижнего прямоугольника:
а) чтобы найти площадь, надо узнать ширину:
4 – 3 = 1 (м)
б) находим площадь:
5 х 1 = 5 (м2)
3) находим площадь шестиугольника:
21 + 5 = 26 (м2)
Ответ: 26 м2 площадь шестиугольника.
Похожие статьи
3 октября 2013
В этом коротком уроке мы научимся считать площади фигур без координатной сетки. Здесь не будет никаких клеточек, никаких пересечений и узлов. Будет только система координат и несколько отмеченных чисел.
Как решать такие задачи? В первую очередь, следует отметить, что у нас все-таки есть линии разметки, а точнее проекции точек на оси координат. И именно они потребуются нам для решения задачи. Причем схема будет даже чуть проще, чем при вычислении площадей методом обводки на координатной сетке. Взгляните на задачу:
Задача B5. Найдите площадь треугольника, изображенного на рисунке.
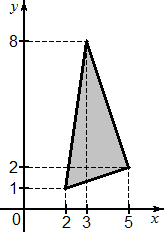
Итак, первый шаг: чертим описанный прямоугольник. Для этого продолжаем линии разметки таким образом, чтобы получилась замкнутая фигура. Это и будет искомый описанный прямоугольник, причем вершины искомой фигуры будут высекать на сторонах этого прямоугольника отдельные отрезки. А значит нам снова нужна формула площади треугольника:
S = 0,5ab
где a и b — катеты (разумеется, речь идет только о прямоугольном треугольнике). А так же пригодится площадь прямоугольника:
S = ab
где a и b — смежные стороны.
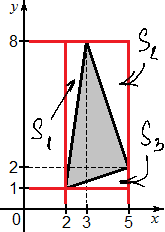
В нашем случае таких треугольников получилось три. Обозначим их S1, S2 и S3. Чтобы сосчитать их площади, нужно сначала найти длину каждого катета. Например, наибольший катер в треугольнике S1 равен a = 8 − 1 = 7, а меньший катет b = 3 − 2 = 1.
Обратите внимание: мы всегда вычитаем из большей абсциссы меньшую, а также из большей ординаты меньшую. Для треугольника S2 верхний катет будет равен a = 5 − 3 = 2, а боковой катет равен b = 8 − 2 = 6. Наконец, для треугольника S3 больший катет будет равен a = 5 − 2 = 3, а меньший катет равен b = 2 − 1 = 1.
Находим площади полученных треугольников:
S1 = 0,5 · 1 · 7 = 3,5;
S2 = 0,5 · 2 · 6 = 6;
S3 = 0,5 · 1 · 3 = 1,5.
Кроме того, нам нужно найти общую площадь описанного прямоугольника. Его стороны равны 7 и 3, а значит площадь равна:
S0 = 7 · 3 = 21.
Осталось выполнить последний шаг. Чтобы найти площадь закрашенной фигуры, нужно из общей площади вычесть площадь дополнительных треугольников, которые мы получили, когда описывали прямоугольник. Получим:
S = S0 − (S1 + S2 + S3) = 21 − (3,5 + 6 + 1,5) = 21 − 11 = 10
Это и является ответом. Площадь закрашенного треугольника равна 10. Как видите, общая схема решения и объем вычислений ничем не отличается от стандартных задач B5 из ЕГЭ по математике, в которых присутствует координатная сетка. Достаточно небольшой тренировки — и вы будете решать эти задачи почти устно.
Смотрите также:
- Задача B5: площадь фигур с вершиной в начале координат

- Опасные ошибки в задачах на площади

- Тест к уроку «Что такое логарифм» (средний)

- Тест к уроку «Площади многоугольников без координатной сетки» (средний)

- Упрощаем решение задач с помощью замены переменной

- Задача B4: расчет времени в пути

