![]()
Условие задачи:
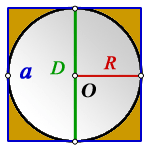
Окружность вписана в квадрат. Найти площадь закрашенной области, если сторона квадрата равна 2 м.
Дано:
Сторона квадрата, a = 2 м
Пояснение к рисунку:
O – центр окружности
R – радиус окружности
D – диаметр окружности
Найти площадь закрашенной области: S
Решение
Площадь искомой области можно выразить как разницу между площадью квадрата и площадью круга

Площадь квадрата

Площадь круга
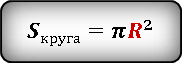
Неизвестен радиус окружности. Из рисунка видно, что сторона квадрата равна диаметру окружности и соответственно удвоенному радиусу
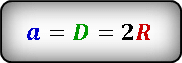
Выразим радиус окружности через сторону квадрата и подставив значение, получим радиус окружности.
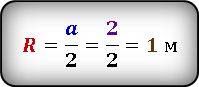
Формула площади искомой области на основании выкладок выше, будет выглядеть следующим образом.

Подставив уже известные значения стороны квадрата и радиуса окружности, получаем.
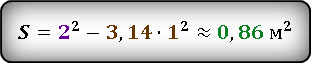
Ответ:

![]() Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Если в уже полученное выражение подставить формулу площади круга выраженную через сторону квадрата и преобразовав, получим следующую формулу, в которой площадь закрашенной области, будет сразу выражена через сторону квадрата.
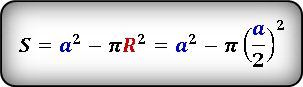
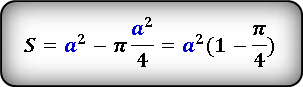
Проверим, подставив наше значение.
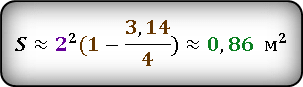
Калькулятор для расчета площади закрашенной области
![]()
- Подробности
-
Опубликовано: 14 сентября 2017
-
Обновлено: 16 октября 2017
Я могу ошибаться, но, по-моему, эта задача пришла в российский интернет из Китая. Кажется, я встречал её на каком-то форуме и там говорилось, что её дают китайским второклассникам. У нас программа несколько другая, поэтому нашим второклассникам я такое давать не решился, но дал пятиклассникам (со всей предысторией про китайцев).
А некоторые из них задали эту задачку своим родителям. Реакция одного из родителей была такой: “Это что правда решают во втором классе?”. Да, решают. Правда, не у нас. Хотя в задаче нет ничего сложного.
В оригинале нам просто дают вот такой рисунок и просят найти заштрихованную площадь.
У детей, как показывает практика, вопросов по рисунку не возникает. Зато у взрослых их хоть отбавляй. Квадрат ли это? А на равные ли прямоугольники разделен квадрат? Поэтому давайте уточним: на рисунке изображен квадрат, в котором проведена диагональ и который разделен на четыре одинаковых вертикальных прямоугольника.
Решать можно по-разному, но не забываем, что это всего лишь второй класс, так что, пожалуйста, без интегралов)
Решение
Сейчас покажу логику, которой по идее должны руководствоваться второклашки, и вы поймете, что задача устная. Просто разделим квадрат на четыре горизонтальных одинаковых прямоугольника. Получится, что большой квадрат состоит из 16 маленьких квадратиков. Площадь каждого маленького квадратика равна единице. Ну и теперь уже нет никаких проблем с вычислением заштрихованной площади. 0,5+0,5+1,5=2,5.
Второклассникам решил такое не давать, потому что с дробями они ещё не знакомы, хотя, что такое половина, понимают и в принципе решить могли бы. Как вам задачка? Сами догадались, как решать? Если у вас был другой вариант решения, пишите в комментариях.
Ещё интересно: Задача из Массачусетского технологического про три пароля. В СССР такие решали в 7 классе
Найти площадь заштрихованной фигуры. Задача для 9 класса, которая не по зубам большинству школьников
Где искать репетитора ребенку и как развить у него логику и нестандартное мышление
Задача: окружность вписана в квадрат , определить площадь закрашенной области
Условие задачи:
Окружность вписана в квадрат. Найти площадь закрашенной области, если сторона квадрата равна 2 м.
Дано:
Сторона квадрата, a = 2 м
Пояснение к рисунку:
O – центр окружности
R – радиус окружности
D – диаметр окружности
Найти площадь закрашенной области: S
Площадь искомой области можно выразить как разницу между площадью квадрата и площадью круга
Неизвестен радиус окружности. Из рисунка видно, что сторона квадрата равна диаметру окружности и соответственно удвоенному радиусу
Выразим радиус окружности через сторону квадрата и подставив значение, получим радиус окружности.
Формула площади искомой области на основании выкладок выше, будет выглядеть следующим образом.
Подставив уже известные значения стороны квадрата и радиуса окружности, получаем.
Ответ:
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Если в уже полученное выражение подставить формулу площади круга выраженную через сторону квадрата и преобразовав, получим следующую формулу, в которой площадь закрашенной области, будет сразу выражена через сторону квадрата.
В квадрат вписана окружность?
Информатика | 10 – 11 классы
В квадрат вписана окружность.
Определите площадь заштрихованной части фигуры, если известен радиус окружности.


s : = sqr(r) * (4 – Pi) / 2 ;

РЕШИТЕ ЗАДАЧУ НА ЯЗЫКЕ ПАСКАЛЬ?
РЕШИТЕ ЗАДАЧУ НА ЯЗЫКЕ ПАСКАЛЬ!
Даны радиусы большой и малой окружности r1, r2.
Найти S заштрихованной фигуры СМОТРИТЕ В ВЛОЖЕНИЯ ФОТО.

Составить алгоритм нахождения площади и длины окружности если известен радиус?
Составить алгоритм нахождения площади и длины окружности если известен радиус.
Составить алгоритм нахождения площади и длины окружности если известен диаметр.
Составить в виде блог – схемы.

Как найти площадь заштрихованной части фигуры?
Как найти площадь заштрихованной части фигуры?

Составить программу для решения следующей задачи : Найти площадь кольца, если заданы радиус внешней окружности и радиус внутренней окружности?
Составить программу для решения следующей задачи : Найти площадь кольца, если заданы радиус внешней окружности и радиус внутренней окружности.

1. Дана сторона равностороннего треугольника?
1. Дана сторона равностороннего треугольника.
Найти площадь этого треугольника и радиусы вписанной и описанной окружностей.

Даны сторона квадрата и радиус окружности?
Даны сторона квадрата и радиус окружности.
Составить программу определяющую у какой фигуры площадь больше.

Вычислить площадь круга и длинну окружности если известен радиус?
Вычислить площадь круга и длинну окружности если известен радиус.

В Pascal ABC?
Найдите радиус окружности если известна площадь окружности.

Определить фигуру с наибольшей площадью : квадрат со стороной a, равносторонний треугольник со стороной b, окружность с радиусом R?
Определить фигуру с наибольшей площадью : квадрат со стороной a, равносторонний треугольник со стороной b, окружность с радиусом R.

С клавиатуры введи радиус окружности?
С клавиатуры введи радиус окружности.
Определи е что больше длина окружности или её S.
Вы зашли на страницу вопроса В квадрат вписана окружность?, который относится к категории Информатика. По уровню сложности вопрос соответствует учебной программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

10 ^ 17 = 100 000 000 000 000 000 (100 квадроллионов) Если у нас 1 000 000 вычеслителей, то в секунду выполняется 1 000 000 операций. Значит операции выполнятся через 100 000 000 000 000 000 / 1 000 000 сек 100 000 000 000 сек 100 000 000 000 / 60 м..

Ответ : 1)Хранение информации во внутренней памяти( мозг человека)Во внешней памяти (тетрадь, флешка)2)Передача информации (источник информации приемник информации)Каналы передачи : информации звуковые волны, почтовая связь, телефонные линии. При пе..

Ровно в два раза, разве нет? 128 : 64 = 2.

1. 3 раза набираем 3 литра в А и сливаем в С. Итого в С получится 9 литров 2. Набираем 3 литра в А и сливаем 1 литр в С. Итого 2 литра в А, 10 литров в С 3. Сливаем 2 литра из А в В 4. Набираем 3 литра в А и сливаем в В Готово : ).

Мама – 4 байт мыла – 4 байт раму – 4 байт итого будет – 12 байт.

Var f1, f2 : text ; a, i, k : integer ; begin assign(f1, ‘input. Txt’) ; reset(f1) ; assign(f2, ‘output. Txt’) ; rewrite(f2) ; readln(f1, a) ; k : = 0 ; for i : = 2 to round(sqrt(a)) do if a mod i = 0 then k : = k + 1 ; if k = 0 then writeln(f2, a.

/ / PascalABC. NET 3. 3, сборка 1562 от 02. 11. 2017 var x, y : int64 ; Begin Readln(x, y) ; Writeln(min(x * 2, y + 20), ‘ ‘, max(x * 2, y + 20)) ; end.

Х = 5 у = 14 5 * 2 = 10 14 + 20 = 34 порядок возрастания : 10, 34.

#include using namespace std ; int main() < int n, max, min, pos1, pos2, mem, sum ; cin >> n ; pos1 = 0 ; pos2 = 0 ; int * A = new int[n] ; for (int i = 0 ; i > A[i] ; > min = A[0] ; max = A[0] ; for (int i = 0 ; i Срочно надо сдать?
Как определить площадь квадрата

О чем эта статья:
3 класс, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Формула нахождения площади квадрата
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.
Если известна длина стороны
Умножаем ее на то же число или возводим в квадрат.
S = a × a = a 2 , где S — площадь, a — сторона.
Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.
Если нам дана диагональ
Возводим ее в квадрат и делим на два.
S = d 2 : 2, где d — диагональ.
Если известен радиус вписанной окружности
Умножаем его квадрат на четыре.
S = 4 × r 2 , где r — это радиус вписанной окружности.
Если у нас есть радиус описанной окружности
Возведем его в квадрат и умножим на два.
S = 2 × R 2 , где R — это радиус описанной окружности.
У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!
Если есть периметр
Мы должны возвести его в квадрат и разделить на 16.
S = Р 2 : 16, где Р — это периметр.
Периметр любого четырехугольника равен сумме длин всех его сторон.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
S квадрата. Решение задач
Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!
Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.
Воспользуемся формулой: S = d 2 : 2.
Подставим в формулу значение диагонали: S = 90 2 : 2 = 4050 мм 2 .
Ответ: 4050 мм 2 .
Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.
Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d
Диаметр окружности равен двум радиусам:
d = 2r
Получается, что сторона равна двум радиусам:
a = 2r
Используем формулу нахождения площади квадрата через сторону:
S = a 2
Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2
Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2
[spoiler title=”источники:”]
http://informatika.my-dict.ru/q/1227729_v-kvadrat-vpisana-okruznost/
http://skysmart.ru/articles/mathematic/ploshad-kvadrata
[/spoiler]
Первый способ:
Всё поле разделено на квадраты со стороной 1 см. То есть площадь такого квадрата 1 кв. см.
Чтобы узнать площадь заштрихованной фигуры, достаточно посчитать количество заштрихованных
квадратов. В первой фигуре их всего 21, значит площадь заштрихованной фигуры 21
кв. см. Площадь второй фигуры попробуй сам вычислить точно так же.
Второй способ несколько длинней:
Мы видим квадрат со стороной 5
см.
Еще мы видим два не заштрихованных прямоугольника с сторонами 1 кв. см и 2 кв. см.
5х5=25 (кв. см) – площадь этого квадрата.
1х2=2 (кв. см) – площадь каждого не заштрихованного прямоугольника.
2х2=4 (кв. см) – площадь всей не заштрихованной части квадрата
Теперь чтобы найти площадь заштрихованной фигуры, нужно от площади квадрата
отнять площадь его не заштрихованной части.
25-4=21 (кв. см).
Площадь второй фигуры попробуй сам вычислить точно так же, с той лишь разницей,
что там изначально дан прямоугольник со сторонами 5 см и 7 см.
The area of the shaded region is the difference between two geometrical shapes which are combined together. By subtracting the area of the smaller geometrical shape from the area of the larger geometrical shape, we will get the area of the shaded region. Or subtract the area of the unshaded region from the area of the entire region that is also called an area of the shaded region.
Area of the shaded region = Area of the large geometrical shape (entire region) – area of the small geometrical shape (shaded region).
Do Refer:
- Area of a Square
- Areas of Irregular Figures
- Area of a Polygon
Follow the below steps and know the process to find out the Area of the Shaded Region. We have given clear details along with the solved examples below.
- Firstly, find out the area of the large geometrical shape or outer region.
- Then, find the area of the small geometrical shape or inner region of the image.
- Finally, subtract an area of the small geometrical shape (entire region) from the large area of the small geometrical shape (shaded region).
- The resultant value is considered as the area of the shaded region.
Area of the Shaded Region Examples
Problem 1.
A regular hexagon is inscribed in a circle with a radius of 21cm. Find out the area of the shaded region?

Solution:
As per the given information,
Hexagon is inscribed in a circle.
Radius of the circle = 21cm.
Area of the circle = A=πr².
Substituting the radius (r) value in the above equation, we will get
A = π(21)².
A = 22 / 7(21 * 21).
A = 22(3*21).
A = 1386.
Area of the circle (A) = 1386 cm².
Area of the hexagon = 3√3/ 2 r².
Substitute the radius value in the above equation, we will get
A = 3√3/ 2 (21)².
A = 3√3/ 2 (441).
A = 1145.75
The area of the hexagon is equal to 1145 cm².
Area of the shaded region = Area of the large geometrical shape – Area of the small geometrical shape.
Area of the shaded region = 1386 – 1145 = 241 cm².
Therefore, the area of the shaded region is equal to 241 cm².
Problem 2.
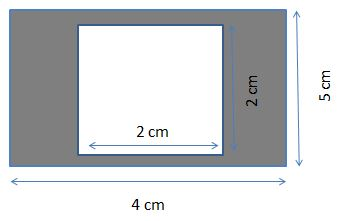
The square is inscribed in a rectangle. The side of the square is 2cm. The length and breadth of the rectangle is 4cm and 5cm. Find out the area of the shaded region?
Solution:
As per the given details,
The Square is inscribed in a rectangle.
Side of the square a = 2cm.
Length of the rectangle (l) = 4cm and breadth of the rectangle (b) =5cm.
Area of the square (A) = a²
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (2)² = 4cm².
Area of the rectangle (A) = l * b
Substitute the length and breadth values in the above equation, we will get
Area of the rectangle (A) = 4cm * 5cm = 20 cm².
Area of the shaded region = Area of the large geometrical shape – area of the small geometrical shape.
Area of the shaded region = 20 – 4 = 16 cm².
Therefore, the Area of the shaded region is equal to 16cm².
Problem 3.
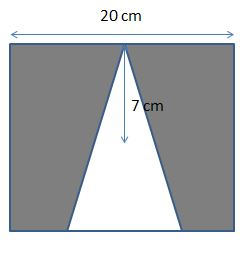
A Triangle is inscribed in a Square. The side of the square is 20cm and the radius of the triangle is 7cm. Calculate the area of the shaded region?
Solution:
As per the given information,
A triangle is inscribed in a square.
Side of the square (a) = 20cm.
Radius of the triangle (r) = 7cm.
Area of the square (A) = a².
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (20)² = 400cm².
Area of the triangle (A)=πr².
Substitute the radius value in the above equation. Then we will get,
A = 22 / 7 (7)².
A = 22 * 7 =154.
The area of the triangle is equal to 154 cm².
Area of the shaded region = Area of the large geometrical shape – area of the small geometrical shape.
Area of the shaded region = 400 – 154 = 246 cm².
Therefore, the Area of the shaded region is equal to 246 cm².
Problem 4.
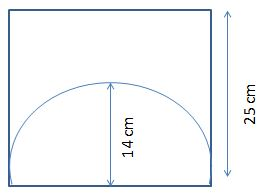
A semi-circle is inscribed in a square with a radius of 14cm. The side of the square is 25cm. Calculate the area of the shaded region?
Solution:
As per the given details,
A semi-circle is inscribed in a square.
Radius of the semi-circle (r) = 14cm.
Side of the square (a) = 25cm.
Area of the square (A) = a².
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (25)² = 625 cm².
Area of the Semi – circle (A) = πr² / 2.
Substitute the radius of the semi-circle in the above equation, we will get
A = 22 / 7 (14)² / 2.
A = 22 / 7 (14 * 14) / 2.
A = 22 (2 * 14) / 2.
A = 22 * 14 = 308.
The area of the semi-circle is equal to 308 cm².
Area of the shaded region = Area of the large geometrical shape – Area of the small geometrical shape.
Area of the shaded region = 625 – 308 = 317 cm².
So, the Area of the shaded region is equal to 317 cm².
FAQs on finding the Area of a Shaded Region
1. What is the Area of the Shaded Region?
It is the difference between the area of the outer region and the inner region.
2. How to find the Area of the Shaded Region?
There are three steps to find the area of the shaded region. They are
i. Calculate the area of the outer region.
ii. Calculate the area of the inner region.
iii. Subtract the area of the inner region from the outer region.
3. What is the Formula for the Area of the Shaded Region?
The formula for the area of the shaded region is
Area of the shaded region = Area of the large geometrical shape (entire region) – area of the small geometrical shape (shaded region).
