Как найти площадь заштрихованной фигуры по клеткам - Сайт, где вы сможете решить свои вопросы

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

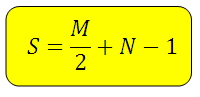
М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:

Отметим узлы:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Рассмотрим подход оговоренный в статье “Площадь четырёхугольника. Универсальный способ“.

Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5

В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Площадь круга равна произведению числа displaystyle pi на квадрат радиуса:
$displaystyle S=pi R^{2}.$
Задача 1. Найдите площадь круга, считая стороны клеток равными 1 (см. рис. 1). В ответе укажите $displaystyle frac{S}{pi }$ .

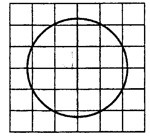
Рис.1

Решение.
Площадь круга равна произведению числа displaystyle pi на квадрат радиуса. Найдём радиус. Из центра проведём радиус . В треугольнике OAB сторона — гипотенуза, катеты равны 1 и 2 (см. рис. 2).

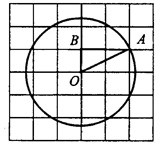
Рис.2

Найдём гипотенузу по теореме Пифагора. $displaystyle OA=sqrt{1^{2}+2^{2}}=sqrt{5}.$
Площадь круга $displaystyle S=pi (sqrt{5})^{2}=5pi .; frac{S}{pi }=frac{5pi }{pi }=5.$
Ответ: 5.
Задача 2. На клетчатой бумаге нарисовано два круга (см. рис. 3). Площадь внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.

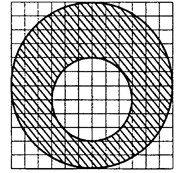
Рис.3

Решение.
Радиус внутреннего круга — 3 клетки, его площадь равна $displaystyle pi R^{2}=3$ . Радиус внешнего круга — 6 клеток, то есть , поэтому его площадь равна $displaystyle pi (2R^{2})=3cdot 4=12.$ Площадь заштрихованной фигуры равна разности 12 — 3 = 9.
Ответ: 9.
Площадь сектора с углом displaystyle alpha градусов равна $displaystyle frac{pi R^{2}alpha }{360^{circ}}.$
Задача 3. Найдите площадь сектора с углом 18 градусов и радиусом 4. В ответе укажите $displaystyle frac{S}{pi }$ .
Решение.
Посчитаем площадь сектора по формуле $displaystyle S=frac{pi R^{2}alpha }{360}=frac{pi cdot 4^{2}cdot 18}{360}=0,8pi cdot frac{S}{pi }=0,8.$
Ответ: 0,8.
Задача 4. Найдите площадь заштрихованного сектора, считая стороны клеток равными 1 (см. рис. 4). В ответе укажите $displaystyle frac{S}{pi }$ .

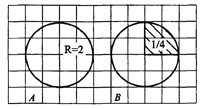
Рис.4

Решение.
На рисунке 4A) площадь круга с радиусом = 2 равна $displaystyle pi R^{2}=pi cdot 2^{2}=4pi .$
На рисунке 4В) площадь сектора составляет $displaystyle frac{1}{4}$ от площади круга (если круг разделить на 4 равные части, то одна из них как раз и будет равна заданному сектору), то есть
$displaystyle frac{pi R^{2}}{4}=frac{pi cdot 2^{2}}{4}=pi.$
Можно было решать задачу по-другому. Площадь сектора равна площади круга, делённой на 4.
displaystyle S:4=4pi :4=pi.
Ответ: 1.
Задача 5. Найдите площадь заштрихованных секторов на рисунках C и D, считая стороны клеток равными 1 (см. рис. 5).

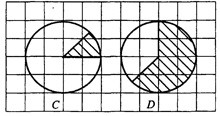
Рис.5

В ответе укажите $displaystyle frac{S}{pi }$ .
Решение. Посчитаем, какая часть круга закрашена. Проведя дополнительные линии (см. рис. 6), видим, что сектор на рисунке 6C) составляет – часть круга, а сектор на рисунке 6D) составляет
$displaystyle frac{5}{8}$ частей круга (круг разделён на 8 равных частей, и закрашено 5 таких частей).
Находим площади секторов на рисунках 6C) и 6D).

Рис.6

1-й способ.
Поделим площадь круга на 8, получим площадь сектора на рисунке 6C), потом умножим эту площадь на 5, получим площадь сектора на рисунке 6D).
$displaystyle S_{C}=4pi :8=0,5pi ;; frac{S}{pi }=0,5;; S_{D}=4pi :8cdot 5=2,5pi ;frac{S}{pi }=2,5.$
Ответ: 0,5 и 2,5.
2-й способ. Найдём площадь $displaystyle frac{1}{8}$ круга.
$displaystyle S_{C}=frac{1}{8}cdot 4pi =0,5pi ;; frac{S}{pi }=0,5;; S_{D}=frac{5}{8}cdot 4pi =2,5pi ;; frac{S}{pi }=2,5.$
Ответ: 0,5 и 2,5.

Источник

Почему бы просто не считать клеточки?

Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.

Вот, например, трапеция:

Посчитаем клеточки: их всего 46, верно?

Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе ( 36+frac{10}{2} = 41)

trapetsiya ploshad po polnym i nepolnym kletochkam

Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…

Как всё это учитывать?

Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.

А жёлтые сколько занимают? Постарайтесь ответить сами.

Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.

Итак, 2 жёлтых куска = 1 клетка.

Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.

Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это ( 36+frac{6}{2}=39) клетки.

Итого клеток: ( 1 + 2 + 39 = 42).

Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.

Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).

Вычислите площадь простых фигур тремя способами

Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.

Вычислите площадь произвольных фигур по формуле Пика

Вычислите самостоятельно площади фигур с помощью формулы Пика:

Посчитайте площадь корабля и котика по формуле Пика

Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!

ploshad teorema pika po kletochkam zadacha 8

ploshad teorema pika po kletochkam zadacha 9

Фигуры с отверстиями — посчитайте площади двумя способами

Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?

Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?

Проверим на простом примере: это квадрат ( 4times 4), и в нём вырезан прямоугольник ( 1times 2), значит, его площадь ( 16-2=14).

А теперь по точкам. На границах (включая внутренние) ( Г = 22). Внутри ( В = 3). Тогда площадь по формуле Пика

( S = frac{22}{2} + 3 -1 = 13.)

Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.

Сосчитай сам и проверь.

Что получилось?

У меня снова на 1 меньше.

Так может быть просто формулу немного «подкрутить»? Нет!

Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.

Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.

Площадь поверхности пирамиды

Для пирамиды тоже действует общее правило:

Площадь полной поверхности пирамиды – это сумма площадей всех граней.( displaystyle {{S}_{полн. пов. }}={{S}_{боков.пов. }}+{{S}_{основания }})

Теперь давай посчитаем площадь поверхности самых популярных пирамид.

Площадь поверхности правильной треугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle {{S}_{ASB}}).

И тогда

( displaystyle {{S}_{полн. пов. }}=3{{text{S}}_{ASB}}+{{text{S}}_{text{осн}.}})

Вспомним теперь, что

( displaystyle {{S}_{осн}}) — это площадь правильного треугольника ( displaystyle ABC).

И еще вспомним, как искать эту площадь.

Используем формулу площади:

( displaystyle S=frac{1}{2}abcdot sin gamma ).

У нас «( displaystyle a)» — это ( displaystyle a), а «( displaystyle b)» — это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).

Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).

Теперь найдем ( displaystyle {{S}_{Delta ASB}}).

Пользуясь основной формулой площади и теоремой Пифагора, находим

( displaystyle {{S}_{Delta ASB}} = frac{1}{2}asqrt{b^2-frac{a^2}{4}})

Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:

( displaystyle S={{a}^{2}}sqrt{3}).

Источник

Поспорил, что найду площадь многоугольника в одно действие за 30 сек. Рассказываю метод

Предмет математики настолько серьезен, что полезно не упустить случая сделать его немного занимательным
(Паскаль)

Добрый день, уважаемые гости и подписчики моего канала!

Вспомнил забавный случай, как около года назад я поспорил с дочкой, что найду площадь любого из представленных выше многоугольников за 30 секунд в одно действие, пока она будет вычислять её множеством действий, как учили в школе.

Выиграл. Дочь проспорила мороженое.

А раз вспомнил об этом, хочу рассказать и Вам, как просто в одно действие используя одну единственную формулу можно точно вычислить площадь многоугольника любой конфигурации и нет необходимости раскладывать фигуру на несколько простейших.

Но, для таких многоугольников есть одно важное условие: каждая вершина должна быть целочисленная, т.е. находиться именно в узле сетки.

Сетка – клеточная поверхность, на которой изображена фигура.

Узел – пересечение линий сетки.

Сетка может быть выполнена с любой единицей измерения, ведь площадь измеряется в квадратах выбранной единицы. Если ячейка 1х1 см., то это 1 кв.см., 1х1 м. – это 1 кв.м. и т.д.

Так вот, существует очень простая формула, которая связывает площадь любого многоугольника с количеством узлов сетки, находящихся на границах отрезков фигуры и внутри самой фигуры. Формулу вывел австрийский математик Георг Александр Пик в 1899 г., в честь которого и называется она формулой (теоремой) Пика:

где:

S – площадь многоугольника;
В – количество узлов внутри фигуры (шт.);
Г – количество узлов, расположенных в вершинах и на отрезках фигуры (шт).

Чтобы стало всё понятно, приведу пример со сложным многоугольником. Нам требуется найти площадь фигуры, представленной ниже:

Теперь, считаем узлы, расположенные внутри, на вершинах и на отрезках фигуры. Это будут значения В и Г, соответственно:

Получаем, что В=16, Г=7, теперь достаточно подставить значения в формулу и получаем: S=Г/2 + В – 1 = 7/2 + 16 -1 = 18,5 кв.ед.

Готово. Площадь равна 18,5 клеток. Вы можете всё перепроверить и будете приятно удивлены!

Плюсы в том, что такая формула легко запоминается и проста в применении! Минус конечно тоже есть, как я упоминал выше – формула не дает точного результата, если хотя бы одна из вершин многоугольника находится вне узла сетки (не целочисленная).

Моя дочь уже с успехом применяет эту формулу на занятиях в школе и быстро находит ответы, хотя некоторые учителя не одобряют такой подход и всё же склоняют к классической схеме: разделить многоугольник на элементарные фигуры, вычислить их площади, пользуясь стандартными формулами и сложив их, получить результат.

Но, всё же думаю, для скорости расчетов – формула полезна. Обязательно расскажите детям!

Очень надеюсь, что статья Вам понравилась! Удачи Вам и добра!

Предлагаю несколько публикаций, которые будут Вам интересны:

Метод быстрого счета. Как в старину перемножали многозначные числа без таблиц умножения? (крестьянский метод)

Какую площадь займет все население планеты, собравшись плечом к плечу? Удивитесь, но этот участок можно объехать за 1 час

Секрет строительного угольника Свенсона. Тригонометрическая зависимость шкал и какие 4 инструмента он объединяет?

Источник

Вычислите площадь простых фигур тремя способами

Вычислите площадь произвольных фигур по формуле Пика

Посчитайте площадь корабля и котика по формуле Пика

Фигуры с отверстиями — посчитайте площади двумя способами

Площадь поверхности пирамиды

Площадь поверхности правильной треугольной пирамиды

Вам также может понравиться

Загар в очках как исправить

Как найти индекс изменения сметной стоимости

Как найти строение атома химического элемента

Добавить комментарий Отменить ответ