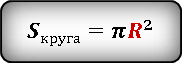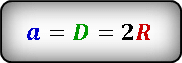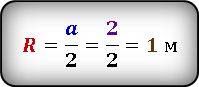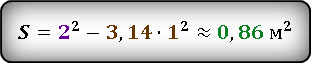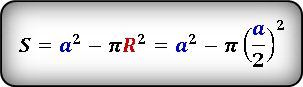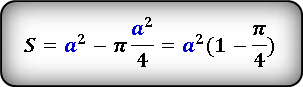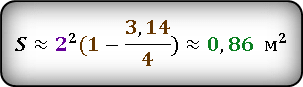Как найти площадь заштрихованной фигуры в квадрате - Сайт, где вы сможете решить свои вопросы

Я могу ошибаться, но, по-моему, эта задача пришла в российский интернет из Китая. Кажется, я встречал её на каком-то форуме и там говорилось, что её дают китайским второклассникам. У нас программа несколько другая, поэтому нашим второклассникам я такое давать не решился, но дал пятиклассникам (со всей предысторией про китайцев).

А некоторые из них задали эту задачку своим родителям. Реакция одного из родителей была такой: “Это что правда решают во втором классе?”. Да, решают. Правда, не у нас. Хотя в задаче нет ничего сложного.

В оригинале нам просто дают вот такой рисунок и просят найти заштрихованную площадь.

"Это что правда решают во 2 классе?" — найти заштрихованную площадь

У детей, как показывает практика, вопросов по рисунку не возникает. Зато у взрослых их хоть отбавляй. Квадрат ли это? А на равные ли прямоугольники разделен квадрат? Поэтому давайте уточним: на рисунке изображен квадрат, в котором проведена диагональ и который разделен на четыре одинаковых вертикальных прямоугольника.

Решать можно по-разному, но не забываем, что это всего лишь второй класс, так что, пожалуйста, без интегралов)

Решение

Сейчас покажу логику, которой по идее должны руководствоваться второклашки, и вы поймете, что задача устная. Просто разделим квадрат на четыре горизонтальных одинаковых прямоугольника. Получится, что большой квадрат состоит из 16 маленьких квадратиков. Площадь каждого маленького квадратика равна единице. Ну и теперь уже нет никаких проблем с вычислением заштрихованной площади. 0,5+0,5+1,5=2,5.

Второклассникам решил такое не давать, потому что с дробями они ещё не знакомы, хотя, что такое половина, понимают и в принципе решить могли бы. Как вам задачка? Сами догадались, как решать? Если у вас был другой вариант решения, пишите в комментариях.

Ещё интересно: Задача из Массачусетского технологического про три пароля. В СССР такие решали в 7 классе

Найти площадь заштрихованной фигуры. Задача для 9 класса, которая не по зубам большинству школьников

Где искать репетитора ребенку и как развить у него логику и нестандартное мышление

Источник

Условие задачи:

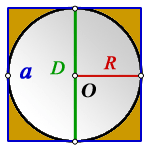
Окружность вписана в квадрат. Найти площадь закрашенной области, если сторона квадрата равна 2 м.

Дано:
Сторона квадрата, a = 2 м

Пояснение к рисунку:
O – центр окружности
R – радиус окружности
D – диаметр окружности

Найти площадь закрашенной области: S

Решение

Площадь искомой области можно выразить как разницу между площадью квадрата и площадью круга

Площадь квадрата

Площадь круга

Неизвестен радиус окружности. Из рисунка видно, что сторона квадрата равна диаметру окружности и соответственно удвоенному радиусу

Выразим радиус окружности через сторону квадрата и подставив значение, получим радиус окружности.

Формула площади искомой области на основании выкладок выше, будет выглядеть следующим образом.

Подставив уже известные значения стороны квадрата и радиуса окружности, получаем.

Ответ:

Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14

Если в уже полученное выражение подставить формулу площади круга выраженную через сторону квадрата и преобразовав, получим следующую формулу, в которой площадь закрашенной области, будет сразу выражена через сторону квадрата.

Проверим, подставив наше значение.

Калькулятор для расчета площади закрашенной области

Подробности

Опубликовано: 14 сентября 2017

Обновлено: 16 октября 2017

Источник

Первый способ:
Всё поле разделено на квадраты со стороной 1 см. То есть площадь такого квадрата 1 кв. см.
Чтобы узнать площадь заштрихованной фигуры, достаточно посчитать количество заштрихованных
квадратов. В первой фигуре их всего 21, значит площадь заштрихованной фигуры 21
кв. см. Площадь второй фигуры попробуй сам вычислить точно так же.

Второй способ несколько длинней:
Мы видим квадрат со стороной 5
см.
Еще мы видим два не заштрихованных прямоугольника с сторонами 1 кв. см и 2 кв. см.

5х5=25 (кв. см) – площадь этого квадрата.
1х2=2 (кв. см) – площадь каждого не заштрихованного прямоугольника.
2х2=4 (кв. см) – площадь всей не заштрихованной части квадрата
Теперь чтобы найти площадь заштрихованной фигуры, нужно от площади квадрата
отнять площадь его не заштрихованной части.
25-4=21 (кв. см).
Площадь второй фигуры попробуй сам вычислить точно так же, с той лишь разницей,
что там изначально дан прямоугольник со сторонами 5 см и 7 см.

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 – 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 – 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 – 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

The area of the shaded region is the difference between two geometrical shapes which are combined together. By subtracting the area of the smaller geometrical shape from the area of the larger geometrical shape, we will get the area of the shaded region. Or subtract the area of the unshaded region from the area of the entire region that is also called an area of the shaded region.

Area of the shaded region = Area of the large geometrical shape (entire region) – area of the small geometrical shape (shaded region).

Do Refer:

Area of a Square
Areas of Irregular Figures
Area of a Polygon

Follow the below steps and know the process to find out the Area of the Shaded Region. We have given clear details along with the solved examples below.

Firstly, find out the area of the large geometrical shape or outer region.
Then, find the area of the small geometrical shape or inner region of the image.
Finally, subtract an area of the small geometrical shape (entire region) from the large area of the small geometrical shape (shaded region).
The resultant value is considered as the area of the shaded region.

Area of the Shaded Region Examples

Problem 1.

A regular hexagon is inscribed in a circle with a radius of 21cm. Find out the area of the shaded region?

Solution:
As per the given information,
Hexagon is inscribed in a circle.
Radius of the circle = 21cm.
Area of the circle = A=πr².
Substituting the radius (r) value in the above equation, we will get
A = π(21)².
A = 22 / 7(21 * 21).
A = 22(3*21).
A = 1386.
Area of the circle (A) = 1386 cm².
Area of the hexagon = 3√3/ 2 r².
Substitute the radius value in the above equation, we will get
A = 3√3/ 2 (21)².
A = 3√3/ 2 (441).
A = 1145.75
The area of the hexagon is equal to 1145 cm².
Area of the shaded region = Area of the large geometrical shape – Area of the small geometrical shape.
Area of the shaded region = 1386 – 1145 = 241 cm².
Therefore, the area of the shaded region is equal to 241 cm².

Problem 2.

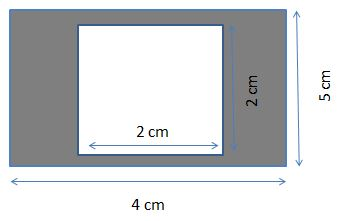
The square is inscribed in a rectangle. The side of the square is 2cm. The length and breadth of the rectangle is 4cm and 5cm. Find out the area of the shaded region?

Solution:

As per the given details,
The Square is inscribed in a rectangle.
Side of the square a = 2cm.
Length of the rectangle (l) = 4cm and breadth of the rectangle (b) =5cm.
Area of the square (A) = a²
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (2)² = 4cm².
Area of the rectangle (A) = l * b
Substitute the length and breadth values in the above equation, we will get
Area of the rectangle (A) = 4cm * 5cm = 20 cm².
Area of the shaded region = Area of the large geometrical shape – area of the small geometrical shape.
Area of the shaded region = 20 – 4 = 16 cm².

Therefore, the Area of the shaded region is equal to 16cm².

Problem 3.

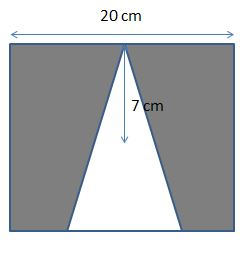
A Triangle is inscribed in a Square. The side of the square is 20cm and the radius of the triangle is 7cm. Calculate the area of the shaded region?

Solution:

As per the given information,
A triangle is inscribed in a square.
Side of the square (a) = 20cm.
Radius of the triangle (r) = 7cm.
Area of the square (A) = a².
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (20)² = 400cm².
Area of the triangle (A)=πr².
Substitute the radius value in the above equation. Then we will get,
A = 22 / 7 (7)².
A = 22 * 7 =154.
The area of the triangle is equal to 154 cm².
Area of the shaded region = Area of the large geometrical shape – area of the small geometrical shape.
Area of the shaded region = 400 – 154 = 246 cm².

Therefore, the Area of the shaded region is equal to 246 cm².

Problem 4.

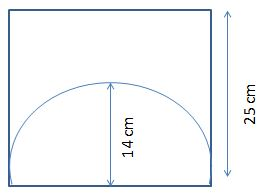
A semi-circle is inscribed in a square with a radius of 14cm. The side of the square is 25cm. Calculate the area of the shaded region?

Solution:

As per the given details,
A semi-circle is inscribed in a square.
Radius of the semi-circle (r) = 14cm.
Side of the square (a) = 25cm.
Area of the square (A) = a².
Substitute the ‘a’ value in the above equation, we will get
Area of the square (A) = (25)² = 625 cm².
Area of the Semi – circle (A) = πr² / 2.
Substitute the radius of the semi-circle in the above equation, we will get
A = 22 / 7 (14)² / 2.
A = 22 / 7 (14 * 14) / 2.
A = 22 (2 * 14) / 2.
A = 22 * 14 = 308.
The area of the semi-circle is equal to 308 cm².
Area of the shaded region = Area of the large geometrical shape – Area of the small geometrical shape.
Area of the shaded region = 625 – 308 = 317 cm².

So, the Area of the shaded region is equal to 317 cm².

FAQs on finding the Area of a Shaded Region

1. What is the Area of the Shaded Region?

It is the difference between the area of the outer region and the inner region.

2. How to find the Area of the Shaded Region?

There are three steps to find the area of the shaded region. They are
i. Calculate the area of the outer region.
ii. Calculate the area of the inner region.
iii. Subtract the area of the inner region from the outer region.

3. What is the Formula for the Area of the Shaded Region?

The formula for the area of the shaded region is
Area of the shaded region = Area of the large geometrical shape (entire region) – area of the small geometrical shape (shaded region).

Источник

Решение

Условие задачи:

Найти площадь закрашенной области: S

Ответ:

Калькулятор для расчета площади закрашенной области

Area of the Shaded Region Examples

FAQs on finding the Area of a Shaded Region

Вам также может понравиться

Как найти угол между векторами с примерами

Как найти вес железного листа

Работа над ошибками как исправить окончание

Добавить комментарий Отменить ответ