Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:

Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса
Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
проведя преобразование, получим:
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
выполнив преобразование, находим:
Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
где h’- высота головки.
Высоту головки приравнивают к m:
Проведя математические преобразования с подстановкой, получим:
Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
где h“- высота ножки зубца.
Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса
Выполнив подстановку в правой части равенства, имеем:
что соответствует формуле:
и если выполнить подстановку, то получим:
Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.

Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Источник
Геометрический расчёт зубчатых колёс



В результате геометрического расчета прямозубых цилиндрических колес (без смещения) определим следующие их параметры (рисунок 2): межосевое расстояние 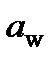 , модуль зубьев m, числа зубьев шестерни z1 и колеса z2, делительные диаметры шестерни
, модуль зубьев m, числа зубьев шестерни z1 и колеса z2, делительные диаметры шестерни 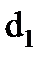 и колеса
и колеса 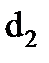 , диаметры окружности вершин
, диаметры окружности вершин 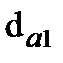 и
и 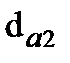 , диаметры окружности впадин
, диаметры окружности впадин 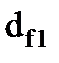 и
и 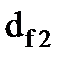 , ширина венцов колеса
, ширина венцов колеса 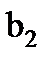 и шестерни
и шестерни 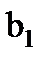 .
.
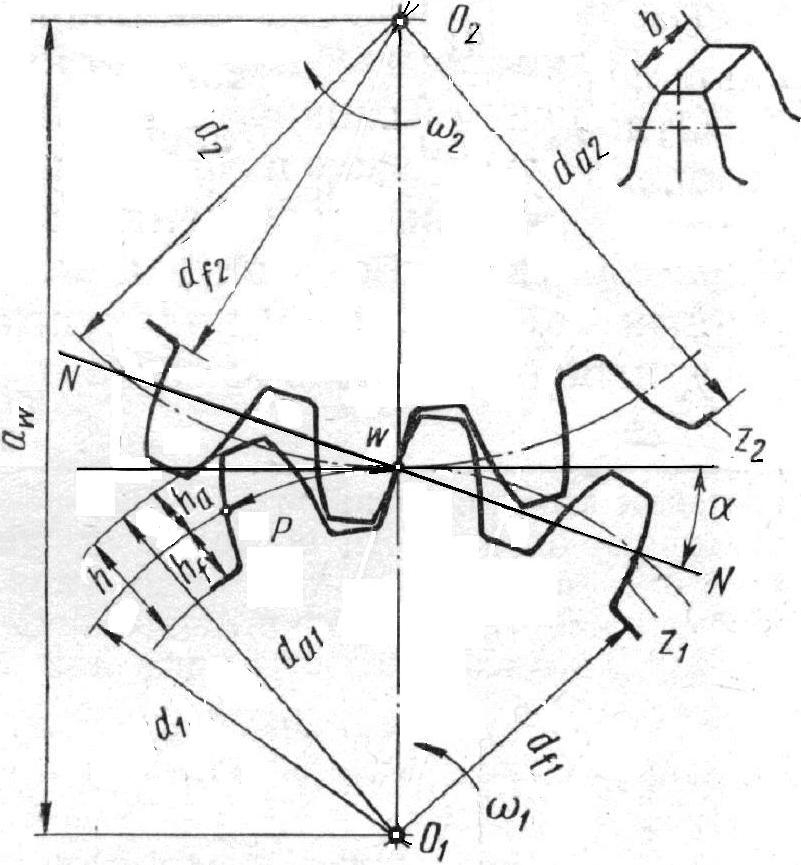
Рисунок 2 — Параметры цилиндрических колес
1) Рассчитаем предварительно межосевое расстояние, выбрав коэффициент ширины колеса 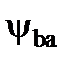 =0,4; полагая, что
=0,4; полагая, что 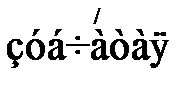 пара расположена симметрично опорам:
пара расположена симметрично опорам:
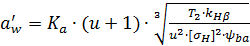 ,
,
где Ка – коэффициент, для прямозубой передачи Ка = 495 МПа 1/3 ;
u – передаточное число редуктора, u = ……;
T2 – вращающий момент на валу колеса, T2 = …. Н·м;
[σH] — допускаемое контактное напряжение, [σH] = 491 МПа;
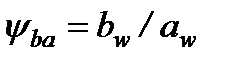 – коэффициент ширины венца зубчатого колеса, рекомендуемые значения
– коэффициент ширины венца зубчатого колеса, рекомендуемые значения 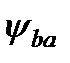 = 0,4;
= 0,4;
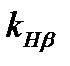 – коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, определяемый в зависимости от расположения колеса по отношению к опорам и коэффициента ширины колеса
– коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, определяемый в зависимости от расположения колеса по отношению к опорам и коэффициента ширины колеса 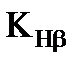 =1,3
=1,3
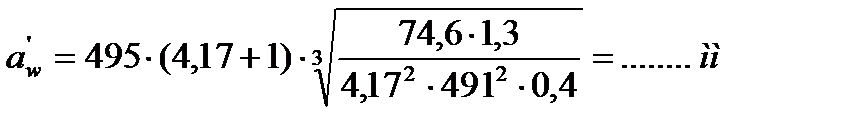 .
.
2) Найдем предварительно делительный диаметр шестерни
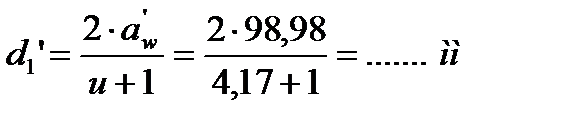 .
.
3) Зададим число зубьев шестерни, учитывая, что zmin =17:
4) Подберем из стандарта величину модуля зубьев, для этого предварительно рассчитаем
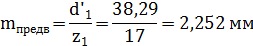
Из ГОСТ 9563-60 (стандартный ряд m: 1; 1,25; 1,5; 1,75; 2; 2,25; 2,5; 2,75; 3; 3,5; 4; 4,5; 5; 5,5; 6; 7)
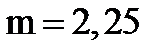 мм.
мм.
5) Найдем число зубьев сопряженного колеса
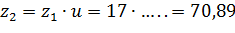 ,
,
6) Рассчитаем геометрические параметры проектируемой передачи при
модуле зубьев m=2,25 мм,
числах зубьев шестерни z1=17 и колеса z2=71:
Фактическое передаточное число
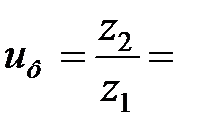
Отклонение от заданного передаточного числа
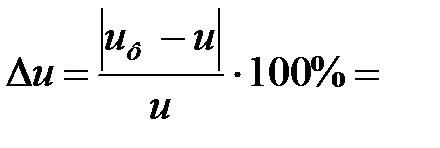
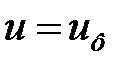
Диаметры делительных окружностей
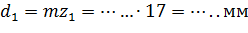 ,
,
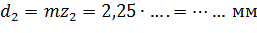 ,
,
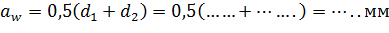
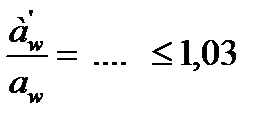 (если
(если 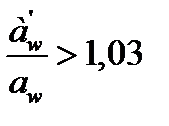 надо задать в п.3) большее число z1 (18, 19, 20 – 30))
надо задать в п.3) большее число z1 (18, 19, 20 – 30))
Диаметры окружностей вершин
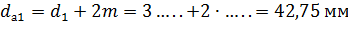 ,
,
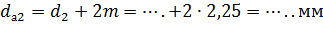 ,
,
Диаметры окружностей впадин
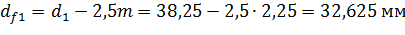 ,
,
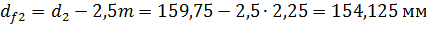 ,
,
Ширину венца шестерни 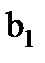 назначаем больше ширины венца колеса
назначаем больше ширины венца колеса 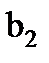 с целью облегчения сборки механизма.
с целью облегчения сборки механизма.
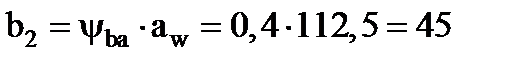 мм,
мм,
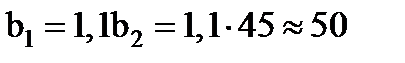 мм,
мм,
В таблице 2 приведены основные параметры 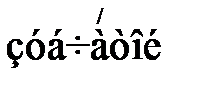 передачи.
передачи.
Окружная скорость вращения колёс в полюсе зацепления (на делительном диаметре)
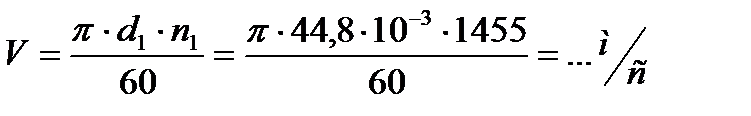 .
.
По рекомендациям (табл. 2.5 в [3]) принимаем степень точности изготовления зубчатых колес 9-В (ГОСТ 1643-81), что означает 9-ю степень кинематической точности, плавности и контакта зубьев; вид сопряжения В (нормальный боковой зазор).
Таблица 2 — Основные параметры 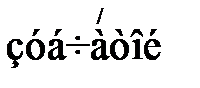 передачи
передачи
| Наименование параметра и размерность | Обозначение | Значение |
Момент на ведомом валу, 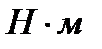 |
Т2 | |
Частота вращения вала, 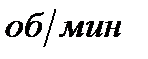 – ведущего – ведомого – ведущего – ведомого |
n1 n2 | |
| Межосевое расстояние, мм | aw | |
| Число зубьев – шестерни – колеса | z1 z2 | |
| Модуль зубьев нормальный, мм | mn | |
| Передаточное число | u | |
| Материал колес, термообработка | cталь 45, улучшение | |
| Твердость рабочих поверхностей зубьев – шестерни – колеса | НВ1 HB2 | |
| Тип передачи | Прямозубая | |
| Угол наклона зуба, град, мин, с | β | |
| Диаметры делительных окружностей, мм – шестерни – колеса | d1 d2 | |
| Ширина зубчатого венца, мм – шестерни – колеса | b1 b2 |
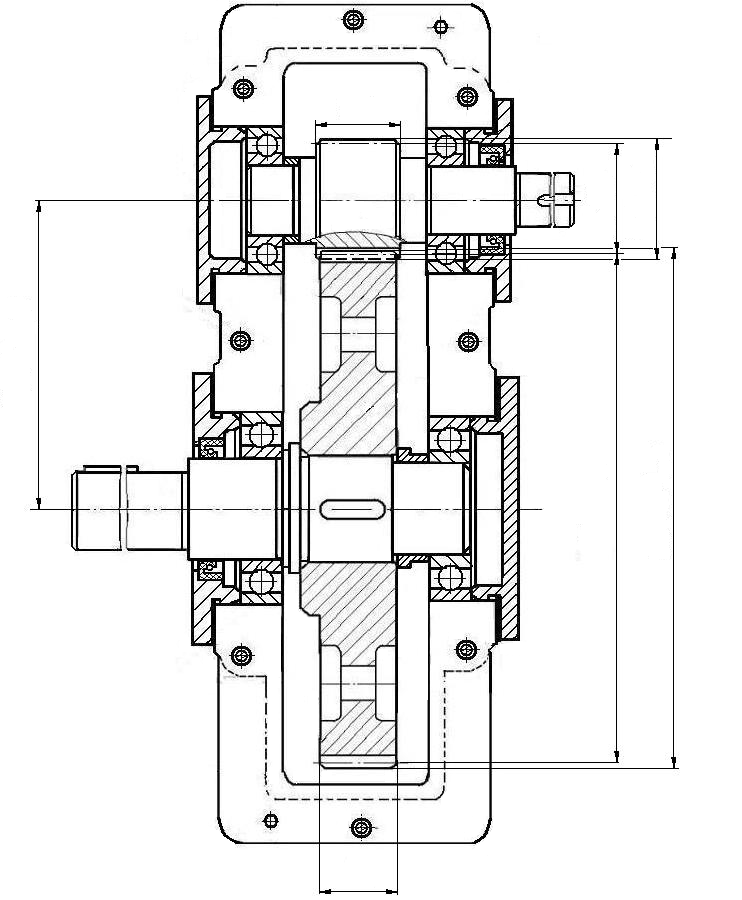
Рисунок 3 – Геометрические параметры зубчатой пары
Источник
На чтение 15 мин Просмотров 6.8к. Опубликовано 27.07.2021
Содержание
- История
- Модуль зубьев зубчатого колеса
- Что такое модуль зубчатого колеса
- Чему равен модуль зубчатого колеса?
- Для чего нужен модуль зубчатого колеса?
- Как определить параметры шестерни?
- Как найти модуль шестерни?
- Как найти делительный диаметр шестерни?
- Как найти модуль зуба?
- Какие бывают модули зубчатых колес?
- Цилиндрические зубчатые колёса
- Продольная линия зуба
- Прямозубые колёса
- Косозубые колёса
- Шевронные колеса
- Колёса с круговыми зубьями
- Винтовые шестерни
- Секторные колёса
- Зубчатые колёса с внешним и внутренним зацеплением
- Звездочка
- Реечная передача (кремальера)
- Коронные колёса
- Конические зубчатые колёса
- Зубчатые передачи
- Типы зубчатых передач
- Эвольвентное зацепление
- Форма зубьев
- Коррегирование зубчатого зацепления
- Зубчатые передачи с точно заданным межосевым расстоянием
- Зубчатые передачи с изменяемым межосевым расстоянием
- Расчетные формулы для зубчатых передач
- Основные параметры зубчатых цилиндрических передач
- Межосевые расстояния
- Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
- Коэффициент запаса прочности при работе зуба двумя сторонами
- Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
- Номинальные передаточные числа
- Почему шестерни часто выполняют заодно с валом?
История
Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Если ведомым будет большее колесо, то на выходе мы потеряем в скорости, но зато крутящий момент этой передачи увеличится. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей. Но сцепление между передаточными колесами с гладким ободом недостаточно жесткое, колёса проскальзывают. Поэтому вместо гладких колес начали использовать зубчатые.
В Древнем Египте для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес [4] .
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:

Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
где h — высота зубца.
где De — диаметр окружности выступов,а z — число зубьев.
Чему равен модуль зубчатого колеса?
Модуль зубчатого колеса Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/p.
Для чего нужен модуль зубчатого колеса?
Что же такое модуль шестерни? это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Как определить параметры шестерни?
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр. Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
Как найти модуль шестерни?
Как определить модуль косозубой шестерни.
Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
Как найти делительный диаметр шестерни?
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса: d = m × z, где z – число зубьев; m – модуль.
Как найти модуль зуба?
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2. Измеряем диаметр: Диаметр окружности выступов (De) равен 28,6 мм.
Какие бывают модули зубчатых колес?
Модуль — это линейная величина, в π раз меньшая шага зубьев p (окружного pt, осевого рx, нормального рn и других шагов) эвольвентного зубчатого колеса m = р/π. Соответственно различают модули: окружной mt, осевой mx, нормальный mn и др.
Цилиндрические зубчатые колёса
Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.
Параметры эвольвентного зубчатого колеса:
- m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:
-
- z — число зубьев колеса
- p — шаг зубьев (отмечен сиреневым цветом)
- d — диаметр делительной окружности (отмечена жёлтым цветом)
- da — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
- db — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
- df — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
- haP+hfP — высота зуба тёмного колеса, x+haP+hfP — высота зуба светлого колеса
Для целей стандартизации, удобства изготовления и замены зубчатых колёс в машиностроении приняты определённые значения модуля зубчатого колеса m, представляющие собой ряд из чисел на выбор: 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 25; 32; 40; 50; 60; 80; 100.
Зубчатые колеса могут быть изготовлены с различным смещением режущей рейки: без смещения (нулевое зубчатое колесо или «с нулевыми зубцами»), с положительным смещением (смещение в сторону увеличения материала), с отрицательным смещением (смещение в сторону уменьшения материала).
Высота головки зуба — haP и высота ножки зуба — hfP — в случае нулевого зубчатого колеса соотносятся с модулем m следующим образом: haP = m; hfP = 1,25 m, то есть:
Отсюда получаем, что высота зуба h (на рисунке не обозначена):
Вообще из рисунка ясно, что диаметр окружности вершин da больше диаметра окружности впадин df на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр da и результат разделить на число зубьев z плюс 2:
Продольная линия зуба
Цилиндрические зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:
Прямозубые колёса
Зубья расположены в радиальных плоскостях, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно. Прямозубые колеса имеют наименьшую стоимость, их работа имеет наивысший КПД, но, в то же время, предельный передаваемый крутящий момент таких колес ниже, чем косозубых и шевронных.
Косозубые колёса
Зубья располагаются под углом к оси вращения, а по форме образуют часть винтовой линии. Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом. Также увеличена площадь контакта, что при тех же размерах с прямозубыми позволяет передавать больший крутящий момент. При работе косозубой пары зацепления возникает механическая осевая сила, направленная вдоль оси вращения каждого колеса и стремящаяся раздвинуть оба колеса в противоположные стороны от плоскости контакта, что обязательно требует применения упорных подшипников. Увеличенная площадь трения зубьев косозубого зацепления вызывает дополнительные потери мощности на нагрев. В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высоких скоростях, либо имеющих жёсткие ограничения по шумности.
Шевронные колеса
Изобретение шевронного профиля зуба часто приписывают Андре Ситроену, однако на самом деле он лишь выкупил патент на более совершенную схему, которую придумал польский механик-самоучка [6] . Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Шевронные колёса решают проблему осевой силы. Осевые силы обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке валов на упорные подшипники. При этом передача является самоустанавливающейся в осевом направлении, по причине чего в редукторах с шевронными колесами один из валов устанавливают на плавающих опорах (как правило — на подшипниках с короткими цилиндрическими роликами).
Колёса с круговыми зубьями
Передача на основе колёс с круговыми зубьями (Передача Новикова) имеет ещё более высокие ходовые качества, чем косозубые — высокую нагрузочную способность зацепления, высокую плавность и бесшумность работы. Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования. Контакт поверхностей зубьев происходит в одной точке на линии зацепления, расположенной параллельно осям колёс.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные колёса
Секторное колесо представляет собой часть обычного цилиндрического колеса с зубьями любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение звена на полный оборот, и поэтому можно сэкономить на его габаритах.
Зубчатые колёса с внешним и внутренним зацеплением
Звездочка
Шестерня-звезда – это основная деталь цепной передачи, которая используется совместно с гибким элементом – цепью для передачи механической энергии.
Реечная передача (кремальера)
![Система Романа Абта[de]), применяется в зубчатой железной дороге](https://tutsvarka.ru/images/wikipedia/commons/thumb/d/d3/SMR_Axle_on_display_at_Llanberis_05-07-24_20.jpeg/im274-320px-SMR_Axle_on_display_at_Llanberis_05-07-24_20.jpeg)
Реечная передача (кремальера) применяется в тех случаях, когда необходимо преобразовать вращательное движение в поступательное и обратно. Состоит из обычной прямозубой шестерни и зубчатой планки (рейки). Работа такого механизма показана на рисунке.
Зубчатая рейка представляет собой часть колеса с бесконечным радиусом делительной окружности. Поэтому делительная окружность, а также окружности вершин и впадин превращаются в параллельные прямые линии. Эвольвентный профиль рейки также принимает прямолинейное очертание. Такое свойство эвольвенты оказалось наиболее ценным при изготовлении зубчатых колёс.
Также реечная передача применяется в зубчатой железной дороге.


Коронные колёса
Коронное колесо — особый вид колёс, зубья которых располагаются на боковой поверхности. Такое колесо, как правило, стыкуется с обычным прямозубым, либо с барабаном из стержней (цевочное колесо), как в башенных часах. Передачи с цевочным колесом — одни из самых ранних и просты в изготовлении, но характеризуются очень большими потерями на трение.
Конические зубчатые колёса

Во многих машинах осуществление требуемых движений механизма связано с необходимостью передать вращение с одного вала на другой при условии, что оси этих валов пересекаются. В таких случаях применяют коническую зубчатую передачу. Различают виды конических колёс, отличающихся по форме линий зубьев: с прямыми, тангенциальными, круговыми и криволинейными зубьями. Конические колёса с круговым зубом, например, применяются в автомобильных главных передачах коробки передач.
Зубчатые передачи

Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Типы зубчатых передач

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
Форма зубьев

Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Коррегирование зубчатого зацепления

Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач

Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Коэффициент запаса прочности при работе зуба двумя сторонами
Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.
Почему шестерни часто выполняют заодно с валом?
Несмотря на это, в редукторах шестерню часто выполняют заодно с валом и даже при толщине, значительно превышающей указанные нормы. Это объясняется большей жесткостью и прочностью, а также технологичностью вала-шестерни, что в конечном итоге оправдывает ее стоимость.
Источники
- https://ru.wikipedia.org/wiki/%D0%97%D1%83%D0%B1%D1%87%D0%B0%D1%82%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D1%81%D0%BE
- https://doctordent.su/pulpit/kak-opredelit-modul-zuba-shesterni-po-diametru.html
- https://novoe-info.ru/chto-takoe-modul-zubchatogo-kolesa/
- https://novoe-info.ru/kak-nayti-modul-zubchatogo-kolesa/
- https://morflot.su/kak-vychislit-modul-zubchatogo-kolesa/
- https://wiki2.org/ru/%D0%97%D1%83%D0%B1%D1%87%D0%B0%D1%82%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D1%81%D0%BE
- https://nzmetallspb.ru/prochee/modul-zubev-zubchatogo-kolesa-raschet-standartnye-opredelenie.html
- https://armatool.ru/modul-zubev-zubcatogo-kolesa-rascet-standartnye-opredelenie/
Расчет зубчатой передачи
Классификация передач. По форме различают цилиндрические, конические, реечные, эллиптические, фигурные зубчатые колеса и с неполным числом зубьев. В зависимости от взаимного расположения; зубчатых колес различают зубчатые передачи с внешним и внутренним зацеплением, а также разделяются на открытые и закрытые (рис. 81).
Назначение. Зубчатые передачи относятся к механическим передачам зацепления с непосредственным контактом и применяются для изменения скорости или направления вращения ведомого звена с соответствующим изменением крутящего момента, получения точных перемещений, при необходимости точного соответствия скоростей и положений ведущего и ведомого звеньев в произвольный момент времени. Зубчатая передача состоит из двух колес с зубьями, посредством которых они сцепляются между собой. Вращение ведущего зубчатого колеса преобразуется во вращение ведомого колеса путем нажатия зубьев первого на зубья второго. Меньшее зубчатое колесо передачи называется шестерней, большее – колесом. Зубчатые передачи могут преобразовывать вращательное движение между валами с параллельными, пересекающимися и перекрещивающимися осями.
|
|
|
|
|
|
а |
б |
в |
г |
|
|
|
|
|
|
д |
е |
ж |
з |
|
|
|
|
|
|
и |
к |
л |
м |
Рис. 81. Виды зубчатых передач: а – внешнего зацепления прямозубая, б – внешнего зацепления косозубая, в – внутреннего зацепления прямозубая, г – внешнего зацепления реечная, д – внешнего зацепления шевронная, е – коническая прямозубая, ж – коническая косозубая, з – коническая круговая, и – коническая круговая – гипоидная, к – внешнего зацепления винтовая, л – передача с круговыми зубьями, м – планетарная.
Преимущества. Важнейшие: компактность, высокий КПД, постоянство передаточного числа, большая долговечность и надежность в работе, возможность осуществления передачи практически любых мощностей при практически любых скоростях и передаточных отношениях, простота обслуживания. Высокая технологичность, которая обусловлена высокопроизводительным специальным оборудованием и технологиями.
Недостатки. Высокие требования к качеству изготовления и монтажа. Шум при больших скоростях. Концентрация напряжений в эвольвентных передачах при точечном контакте и чувствительность к ошибкам монтажа в передачах с линейным контактом. Поэтому для реализации преимуществ при изготовлении деталей необходимо применять высококачественные материалы и технологии изготовления.
Сферы применения. 3убчатые передачи нашли самое широкое распространение среди механических передач в машинах различных отраслей. Назначение и конструкции зубчатых передач разнообразны. Их применяют во многих приборах и почти во всех машинах, в том числе и самых тяжелых и мощных для передачи мощностей до 65 тыс.кВТ (65МВт), с диаметром колес от долей миллиметра до 6м и более. Окружная скорость зубьев может достигать 270м/с. Передаточные отношения для открытой передачи принимают ![]() 10, а для закрытой
10, а для закрытой ![]() 25. КПД одной ступени зубчатой передачи при высоком качестве изготовления и монтажа может достигать
25. КПД одной ступени зубчатой передачи при высоком качестве изготовления и монтажа может достигать ![]() 0,99.
0,99.
Геометрический расчет. Передаточное отношение передачи
![]() , (14.1)
, (14.1)
где ![]() – число зубьев шестерни и колеса соответственно.
– число зубьев шестерни и колеса соответственно.
Номинальные значения передаточных чисел и зубчатых редукторов общего назначения, выполненных в виде самостоятельных агрегатов стандартизированы:
1-й ряд 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0;12,5.
2-й рад 1,12; 1,40; 1,80; 2,24; 2,80; 3,55; 4,5; 5,6; 7,1; 9,0; 11,2.
При выборе стандартных параметров первый ряд предпочтительнее второго, а принятые значения передаточных чисел не должны отличаться от расчетных не более чем на 3%.
Расстояние между осями зубчатых колес цилиндрической передачи по межосевой линии называется межосевым расстоянием:
![]() , (14.2)
, (14.2)
где ![]() и
и ![]() – начальные диаметры шестерни и колеса; знак плюс относится к передаче с внешним зацеплением, а минус – к передаче с внутренним зацеплением.
– начальные диаметры шестерни и колеса; знак плюс относится к передаче с внешним зацеплением, а минус – к передаче с внутренним зацеплением.
Стандартизированы номинальные значения межосевых расстояний aw, мм:
1-й ряд 40; 50; 63; 80100; 125; 160; 200; 250; 315; 400; 500; 630; 800
2-й ряд – – 71; 98; 112; 140; 180; 225; 280; 355; 450; 560; 710; 900.
Межосевое расстояние цилиндрической зубчатой передачи, равное полусумме делительных диаметров колеса d2 и шестерни ![]() при внешнем зацеплении или полуразности при внутреннем зацеплении, называется делительным межосевым расстоянием:
при внешнем зацеплении или полуразности при внутреннем зацеплении, называется делительным межосевым расстоянием:
![]() . (14.3)
. (14.3)
Делительные диаметры для зубчатых колес прямозубой передачи
d = zm, (14.4)
для косозубой и шевронной
![]() . (14.5)
. (14.5)
где т – модуль зацепления основная характеристика размеров зубчатых и червячных колес. Для обеспечения взаимозаменяемости и унификации инструмента для изготовления модули цилиндрические и конические эвольвентных зубчатых колес стандартизованы: для цилиндрических колес – значения нормальных модулей, для конических – значения окружных делительных модулей в диапазоне 0,05..100мм.
1-й ряд 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25;
2-й ряд 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22; 28.
Ширина венца цилиндрического зубчатого колеса определяется по одной из формул
![]() , (14.6)
, (14.6)
или
![]() , (14.7)
, (14.7)
где ![]() – коэффициент ширины зубчатого венца по межосевому расстоянию, а
– коэффициент ширины зубчатого венца по межосевому расстоянию, а ![]() – коэффициент ширины зубчатого венца по диаметру шестерни.
– коэффициент ширины зубчатого венца по диаметру шестерни.
Коэффициенты ![]() и
и ![]() связаны зависимостью:
связаны зависимостью:
![]() . (14.8)
. (14.8)
Значения коэффициентов ширины венца зубчатых колес ![]() по межосевому расстоянию выбираются из стандартного ряда: 0,1; 0,125; 0,16; 0,2; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,000; 1,25 и т. д.
по межосевому расстоянию выбираются из стандартного ряда: 0,1; 0,125; 0,16; 0,2; 0,250; 0,315; 0,400; 0,500; 0,630; 0,800; 1,000; 1,25 и т. д.

Рис. 82. Обозначения элементов зубчатого зацепления.
Для заданного числа зубьев ![]() и
и ![]() , коэффициентов смещения исходного контура
, коэффициентов смещения исходного контура ![]() и
и ![]() , угла наклона зубьев
, угла наклона зубьев ![]() основные параметры эвольвентных цилиндрических колес внешнего зацепления, показанные на рис 82 в соответствии с ГОСТ 13755-81 определяются по расчетным формулам:
основные параметры эвольвентных цилиндрических колес внешнего зацепления, показанные на рис 82 в соответствии с ГОСТ 13755-81 определяются по расчетным формулам:
|
Параметр |
Шестерня |
Колесо |
|
Делительный диаметр |
|
|
|
Основной диаметр |
|
|
|
Начальный диаметр |
|
|
|
Диаметр вершин зубьев |
|
|
|
Диаметр впадин зубьев |
|
|
|
Межосевое расстояние |
|
|
|
Делительный угол профиля в торцевом сечении |
|
|
|
Коэффициент торцевого перекрытия |
|
|
|
Рабочая ширина зубчатого венца |
|
|
|
Коэффициент осевого перекрытия (при ширине венца |
|
|
|
Основной угол наклона |
|
Кинематический и силовой расчет. Расчетная окружная скорость v цилиндрической передачи:
– шестерни ![]() ; (14.9)
; (14.9)
– колеса ![]() ,
,
где ![]() – угловая скорость зубчатого колеса; п – частота вращения зубчатого колеса;
– угловая скорость зубчатого колеса; п – частота вращения зубчатого колеса; ![]() – начальный диаметр цилиндрического зубчатого колеса.
– начальный диаметр цилиндрического зубчатого колеса.
Окружная сила цилиндрической зубчатой передачи Ft
 , (14.10)
, (14.10)
где ![]() – крутящий момент на шестерне.
– крутящий момент на шестерне.
Сила давления между зубьями в цилиндрической прямозубой передаче
![]() . (14.11)
. (14.11)
 Составляющие этой силы: в цилиндрических прямозубых (рис. 83) и шевронных передачах – окружная сила
Составляющие этой силы: в цилиндрических прямозубых (рис. 83) и шевронных передачах – окружная сила ![]() , и радиальная сила
, и радиальная сила ![]() , в конической прямозубой и цилиндрической косозубой передачах – окружная сила
, в конической прямозубой и цилиндрической косозубой передачах – окружная сила ![]() , радиальная сила
, радиальная сила ![]() , и осевая сила Fa.
, и осевая сила Fa.
Радиальная сила в цилиндрической передаче
![]() , (14.12)
, (14.12)
Осевая сила, действующая на колесо косозубой цилиндрической передачи
![]()
![]() , (14.13)
, (14.13)
Критерии работоспособности зубчатых передач. Учитывая виды повреждений критериями работоспособности зубчатых передач являются контактная и изгибная прочность зубьев. Проектный расчет закрытых передач малой и средней твердости выполняется на контактную выносливость. Расчет на изгибную прочность зубьев в этом случае выполняется как проверочный. Для зубчатых колес высокой прочности (![]() ) размеры передачи определяются из расчета зубьев на изгиб, а проверочный расчет выполняется по контактным напряжениям. Для открытой передачи проектный расчет выполняется из условия предупреждения поломки зуба с учетом износа зубьев, проверочный расчет выполняется из условия обеспечения контактной прочности.
) размеры передачи определяются из расчета зубьев на изгиб, а проверочный расчет выполняется по контактным напряжениям. Для открытой передачи проектный расчет выполняется из условия предупреждения поломки зуба с учетом износа зубьев, проверочный расчет выполняется из условия обеспечения контактной прочности.
Проектные расчеты зубчатых передач.
Расчет зубьев на контактную прочность выполняют для зацепления в полюсе, так как выкрашивание зубьев начинается у полюсной линии. По зависимости для проектного расчета на контактную прочность зубьев определяется межосевое расстояние
 , (14.14)
, (14.14)
где ![]() – коэффициент для прямозубых передач Ка = 495, а для косозубых Ка= 430,
– коэффициент для прямозубых передач Ка = 495, а для косозубых Ка= 430, ![]() – момент на зубчатом колесе передачи в
– момент на зубчатом колесе передачи в ![]() ,
, ![]() – коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев, который определяется по рис. 84;
– коэффициент неравномерности распределения нагрузки по длине контактных линий в результате погрешностей в зацеплении и деформации зубьев, который определяется по рис. 84; ![]() – допускаемое контактное напряжение в МПа.
– допускаемое контактное напряжение в МПа.

Рис.84. Коэффициенты неравномерности распределения нагрузки по длине контактных линий ![]() для расчета на контактную прочность.
для расчета на контактную прочность.
Коэффициент ширины венца по межосевому расстоянию ![]() для редукторов принимают равным: для зубчатых колес из улучшенных сталей при несимметричном расположении
для редукторов принимают равным: для зубчатых колес из улучшенных сталей при несимметричном расположении ![]() = 0,315…0,4; для зубчатых колес из закаленных сталей
= 0,315…0,4; для зубчатых колес из закаленных сталей ![]() = 0,25…0,315; при симметричном расположении зубчатых колес относительно опор
= 0,25…0,315; при симметричном расположении зубчатых колес относительно опор ![]() = 0,4…0,5; для передвижных зубчатых колес коробок скоростей
= 0,4…0,5; для передвижных зубчатых колес коробок скоростей ![]() = 0,1…0,2. Принимаются стандартные значения
= 0,1…0,2. Принимаются стандартные значения ![]() .
.
Допускаемое контактное напряжение
![]() , (14.15)
, (14.15)
где ![]() – предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений (табл. 14.1);
– предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений (табл. 14.1); ![]() – коэффициент безопасности; ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; Zv – коэффициент, учитывающий окружную скорость передачи; KHL – коэффициент долговечности. Коэффициент безопасности зубчатых колес с однородной структурой материала sH = 1,1; с поверхностным упрочением зубьев sH = 1,2. Коэффициент ZR = 0,9…1; ZR =1,0 при
– коэффициент безопасности; ZR – коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; Zv – коэффициент, учитывающий окружную скорость передачи; KHL – коэффициент долговечности. Коэффициент безопасности зубчатых колес с однородной структурой материала sH = 1,1; с поверхностным упрочением зубьев sH = 1,2. Коэффициент ZR = 0,9…1; ZR =1,0 при ![]() мкм, ZR =0,95 при
мкм, ZR =0,95 при ![]() мкм и ZR =0,9 при
мкм и ZR =0,9 при ![]() мкм. Коэффициент Zv = 1…1.16; чем меньше скорость передачи и тверже зубья, тем меньше Zv. При v << 5м/с Zv = 1. При приближенном расчете можно принимать
мкм. Коэффициент Zv = 1…1.16; чем меньше скорость передачи и тверже зубья, тем меньше Zv. При v << 5м/с Zv = 1. При приближенном расчете можно принимать ![]() .
.
Коэффициент долговечности KHL определяют в зависимости от отношения ![]() – базового числа циклов нагружения при котором определяется предел контактной выносливости и
– базового числа циклов нагружения при котором определяется предел контактной выносливости и ![]() – эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. Базовое число циклов напряжений в зубьях принимают в зависимости от твердости НВ рабочей поверхности зубьев либо по формуле
– эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. Базовое число циклов напряжений в зубьях принимают в зависимости от твердости НВ рабочей поверхности зубьев либо по формуле
![]() . (14.16)
. (14.16)
При эквивалентном числе циклов нагужения зубьев колес больше базового ![]() коэффициент долговечности KHL =1. В случае когда эквивалентное число циклов
коэффициент долговечности KHL =1. В случае когда эквивалентное число циклов
нагружения зубьев меньше базового то
 . (14.17)
. (14.17)
Если при расчете колес из нормализованной или улучшенной стали ![]() , то принимают
, то принимают ![]() .
.
Таблица 14.1. Предел контактной выносливости при базовом числе циклов
|
Термическая обработка |
Твердость поверхностей зубьев |
|
|
Нормализация или улучшение |
|
|
|
Объемная закалка |
|
|
|
Поверхностная закалка |
|
|
|
Цементация или нитроцементация |
|
|
|
Азотирование |
|
|
Эквивалентное число циклов напряжений при работе передачи с постоянной нагрузкой
![]() , (14.18)
, (14.18)
где с – число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; ![]() – частота вращения рассчитываемого зубчатого колеса,
– частота вращения рассчитываемого зубчатого колеса, ![]() ; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.
; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.
При работе передачи с переменными нагрузками
![]() , (14.19)
, (14.19)
где Tmax – максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; ![]() – передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения
– передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения ![]() .
.
Допускаемое контактное напряжение ![]() для зубьев прямозубых передач определяют раздельно для шестерни и колеса и в качестве расчетного принимают меньшее из них. При расчете зубьев косозубых передач, в которых зубья шестерни значительно превышают твердость зубьев колеса, расчетное контактное напряжение
для зубьев прямозубых передач определяют раздельно для шестерни и колеса и в качестве расчетного принимают меньшее из них. При расчете зубьев косозубых передач, в которых зубья шестерни значительно превышают твердость зубьев колеса, расчетное контактное напряжение
![]() , (14.20)
, (14.20)
где ![]() и
и ![]() – допускаемые контактные напряжения зубьев шестерни и колеса, вычисляемые по формуле (14.15);
– допускаемые контактные напряжения зубьев шестерни и колеса, вычисляемые по формуле (14.15); ![]() – минимальное допускаемое напряжение из этих двух допускаемых напряжений.
– минимальное допускаемое напряжение из этих двух допускаемых напряжений.
Полученный по формуле (14.14) межосевое расстояние ![]() следует округлить до ближайшего большего стандартного значения. При проектировочном расчете числом зубьев
следует округлить до ближайшего большего стандартного значения. При проектировочном расчете числом зубьев ![]() шестерни задаются, а число зубьев колеса
шестерни задаются, а число зубьев колеса ![]() . Для зубчатых передач без смещения рекомендуется принимать
. Для зубчатых передач без смещения рекомендуется принимать ![]() зубьев для обеспечения отсутствия подрезание зубьев. Для уменьшения габаритных размеров тихоходных зубчатых передач допускается
зубьев для обеспечения отсутствия подрезание зубьев. Для уменьшения габаритных размеров тихоходных зубчатых передач допускается ![]() зубьев. В быстроходных передачах в целях уменьшения шума рекомендуется принимать
зубьев. В быстроходных передачах в целях уменьшения шума рекомендуется принимать ![]() зубьев.
зубьев.
Расчет зубьев на изгибную прочность. Предварительное значение модуля зубчатой передачи определяется из условия проектного расчета зубьев на изгиб.
 , (14.21)
, (14.21)

Рис. 85. Коэффициент формы зуба.
где ![]() – коэффициент для прямозубых передач
– коэффициент для прямозубых передач ![]() =14, для косозубых и шевронных
=14, для косозубых и шевронных ![]() =11,2;
=11,2; ![]() – коэффициентом формы зуба, который определяется по рис.85;
– коэффициентом формы зуба, который определяется по рис.85; ![]() – коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, который определяется по рис.86;
– коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, который определяется по рис.86; ![]() – момент на шестерне передачи в
– момент на шестерне передачи в ![]() ,
, ![]() – число зубьев шестерни; а
– число зубьев шестерни; а ![]() – коэффициент ширины зубчатого венца по диаметру шестерни, который определяется по формуле (14.8),
– коэффициент ширины зубчатого венца по диаметру шестерни, который определяется по формуле (14.8), ![]() допускаемые напряжения при изгибе зубьев.
допускаемые напряжения при изгибе зубьев.
Для косых зубьев коэффициент YF определяют не по действительному числу зубьев z, а по эквивалентному ![]() по зависимости
по зависимости
![]() . (14.22)
. (14.22)
Допускаемое напряжение на изгиб для зубьев
![]() , (14.23)
, (14.23)
где ![]() – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений (табл.14.2);
– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений (табл.14.2); ![]() – коэффициент безопасности зубьев на изгиб;
– коэффициент безопасности зубьев на изгиб; ![]() – коэффициент долговечности зубьев на изгиб;
– коэффициент долговечности зубьев на изгиб; ![]() – коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья;
– коэффициент, учитывающий влияние двустороннего приложения нагрузки на зубья; ![]() ; коэффициент безопасности
; коэффициент безопасности ![]() =1,7…2,2 (большие значения для литых заготовок).
=1,7…2,2 (большие значения для литых заготовок).

Рис. 86. Коэффициенты неравномерности распределения нагрузки по длине контактных линий для расчета на изгибную прочность. Схемы расположения колес показаны на рис.84.
Таблица 14.2 Пределы выносливости материалов зубчатых колес на изгиб
|
Вид термообработки и марка стали |
Твердость зубьев |
|
|
|
на поверхности |
в сердцевине |
||
|
Цементация легированных сталей: |
|||
|
содержание Ni более 1% Cr 1% и менее (например, 20ХН2М, 12ХН2, 12ХН3А) |
57-63 |
32-45 |
950 |
|
стали марок 18ХГТ, 30ХГТ, 12Х2Н4А и др. |
57-63 |
32-45 |
800 |
|
Нитроцементация легированных сталей: |
|||
|
25ХГМ |
57-63 |
32-45 |
1000 |
|
25ХГТ, 30ХГТ и др. |
57-63 |
32-45 |
750 |
|
Заделка при нагреве ТВЧ по всему контуру: |
|||
|
стали пониженной прокаливаемости (например, 55ПП) |
58-62 |
28-35 |
900 |
|
стали марок 60ХВ, 60ХН и др. |
54-60 |
25-35 |
700 |
|
стали марок 35ХМА, 40ХН и др. |
48-60 |
25-35 |
600 |
|
Нормализация или улучшение |
НВ |
180-350 |
1,35НВ+100 |
|
Азотирование легированных сталей |
– |
24-40 |
18HRCсерд+50 |
Коэффициент долговечности ![]() определяют в зависимости от отношения
определяют в зависимости от отношения ![]() – базового числа циклов нагружения при котором определяется предел контактной выносливости и
– базового числа циклов нагружения при котором определяется предел контактной выносливости и ![]() – эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. При эквивалентном числе циклов нагружения зубьев колес больше базового
– эквивалентного числа нагружения зубьев передачи с учетом режима ее работы. При эквивалентном числе циклов нагружения зубьев колес больше базового ![]() коэффициент долговечности
коэффициент долговечности ![]() =1.
=1.
В случае когда эквивалентное число циклов нагружения зубьев меньше базового, то
 . (14.24)
. (14.24)
Для зубчатых колес с твердостью поверхности зубьев ![]() , а также со шлифованной переходной поверхностью зубьев показатель корня т=6, для зубчатых колес с
, а также со шлифованной переходной поверхностью зубьев показатель корня т=6, для зубчатых колес с ![]() и нешлифованной переходной поверхностью т=9. Базовое число циклов нагружений зубьев изгибом
и нешлифованной переходной поверхностью т=9. Базовое число циклов нагружений зубьев изгибом ![]() .
.
Эквивалентное число циклов перемены напряжений NFE. при работе передачи с постоянной нагрузкой
![]() , (14.25)
, (14.25)
где с – число одинаковых зубчатых колес, сцепляющихся с рассчитываемым зубчатым колесом; ![]() – частота вращения рассчитываемого зубчатого колеса,
– частота вращения рассчитываемого зубчатого колеса, ![]() ; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.
; t – продолжительность работы передачи под нагрузкой за расчетный срок службы, ч.
При работе передачи с переменными нагрузками
![]() , (14.26)
, (14.26)
где Tmax – максимальный крутящий момент, передаваемый зубчатым колесом в течение времени t0 за весь срок службы передачи при частоте вращения колеса п0; ![]() – передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения , показатель степени принимается согласно рекомендациям к формуле (14.24).
– передаваемые зубчатым колесом крутящие моменты в течение времени соответственно при частоте вращения , показатель степени принимается согласно рекомендациям к формуле (14.24).
Значение коэффициента ![]() принимают: при односторонней нагрузке на зубья
принимают: при односторонней нагрузке на зубья ![]() , а при двусторонней
, а при двусторонней ![]() = 0,7…0,8 (большее значение при НВ > 350).
= 0,7…0,8 (большее значение при НВ > 350).
При известном межосевом расстоянии ориентировочное значение модуля передачи определяется по зависимости
![]() , (14.27)
, (14.27)
где ![]() – коэффициент для прямозубой передачи
– коэффициент для прямозубой передачи ![]() =1400, для косозубой и шевронной
=1400, для косозубой и шевронной ![]() =850.
=850.
Значение модуля зацепления полученное по формуле (14.27) округляется до ближайшего стандартного значения. После определения значений межосевого расстояния ![]() и модуля
и модуля ![]() определяются число зубьев и все геометрические параметры передачи по которым выполняется проверочные расчеты.
определяются число зубьев и все геометрические параметры передачи по которым выполняется проверочные расчеты.
Проверочные расчеты зубчатых передач.
Расчет зубьев на контактную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости
– для прямозубых передач
 ; (14.28)
; (14.28)
– для косозубых передач
 , (14.29)
, (14.29)
где ![]() ,
, ![]() – коэффициент неравномерности распределения нагрузки между зубьями в зависимости от скорости и точности изготовления;
– коэффициент неравномерности распределения нагрузки между зубьями в зависимости от скорости и точности изготовления; ![]() – коэффициент динамической нагрузки, возникающей в зацеплении.
– коэффициент динамической нагрузки, возникающей в зацеплении.
Таблица 14.3 Значения коэффициента динамических нагрузок ![]()
|
Степень точности |
Твердость поверхностей зубьев |
υ, м/с |
|||||
|
1 |
2 |
4 |
6 |
8 |
10 |
||
|
6-я |
а |
||||||
|
б |
|||||||
|
7-я |
а |
||||||
|
б |
|||||||
|
8-я |
а |
||||||
|
б |
|||||||
|
9-я |
а |
||||||
|
б |
Примечания: 1. Твердость поверхности зубьев: а) ![]() и
и ![]() или
или ![]() и
и ![]() ; б)
; б) ![]() и
и ![]() . 2. 3начения
. 2. 3начения ![]() в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.
в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.

Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями ![]() : а – для расчета на контактную прочность, b – для расчета на изгибную прочность.
: а – для расчета на контактную прочность, b – для расчета на изгибную прочность.
Коэффициент неравномерности распределения нагрузки для прямозубых передач принят КНа = 1, а для косозубых коэффициент ![]() определяются по графикам на рис.87. Коэффициент динамической нагрузки
определяются по графикам на рис.87. Коэффициент динамической нагрузки ![]() определяют по таблице 14.3.
определяют по таблице 14.3.
Рис. 87.Коэффициенты неравномерности распределения нагрузки между зубьями ![]() : а – для расчета на контактную прочность, b – для расчета на изгибную прочность.
: а – для расчета на контактную прочность, b – для расчета на изгибную прочность.
При действии на зубья кратковременных перегрузок выполняется проверка рабочих поверхностей зубьев на контактную прочность по максимальному контактному напряжению:
 , (14.30)
, (14.30)
где ![]() – максимальное расчетное напряжение при перегрузке зубьев максимальным моментом
– максимальное расчетное напряжение при перегрузке зубьев максимальным моментом ![]() ;
; ![]() – допускаемое максимальное контактное напряжение для зубьев;
– допускаемое максимальное контактное напряжение для зубьев; ![]() – расчетное контактное напряжение, вызываемое расчетным моментом
– расчетное контактное напряжение, вызываемое расчетным моментом ![]() и определяемое по формуле (14.27) или (14.28). Для зубьев зубчатых колес и термообработкой нормализацией, улучшением или объемной закалкой с отпуском
и определяемое по формуле (14.27) или (14.28). Для зубьев зубчатых колес и термообработкой нормализацией, улучшением или объемной закалкой с отпуском ![]() , где
, где ![]() – предел текучести материала зубьев при растяжении; для зубьев с термообработкой – цементация, контурная закалка после нагрева ТВЧ –
– предел текучести материала зубьев при растяжении; для зубьев с термообработкой – цементация, контурная закалка после нагрева ТВЧ – ![]() ; для азотированных зубьев
; для азотированных зубьев ![]() . Расчет зубьев по формуле (14.30) производится раздельно для колеса и для шестерни.
. Расчет зубьев по формуле (14.30) производится раздельно для колеса и для шестерни.
Расчет зубьев на изгибную прочность выполняется по известным геометрическим параметрам передачи при выбранной степени точности изготовления зубьев колес по зависимости
![]() , (14.31)
, (14.31)
где ![]() – коэффициент учитывающий перекрытие зубьев;
– коэффициент учитывающий перекрытие зубьев; ![]() – коэффициент наклона зубьев;
– коэффициент наклона зубьев; ![]() – коэффициент распределения нагрузки между зубьями;
– коэффициент распределения нагрузки между зубьями; ![]() – коэффициент динамической нагрузки, возникающей в зацеплении при работе передачи,
– коэффициент динамической нагрузки, возникающей в зацеплении при работе передачи, ![]() – коэффициент ширины венца зубчатого колеса по начальному диаметру шестерни.
– коэффициент ширины венца зубчатого колеса по начальному диаметру шестерни.
При подстановке окружной силы ![]() по зависимости (14.10) формула (14.31) преобразуется к виду
по зависимости (14.10) формула (14.31) преобразуется к виду
![]() .
.
Коэффициент, учитывающий перекрытие зубьев
![]() .
.
При приближенных расчетах для для косозубых передач и прямозубых передач принимают ![]() .
.
Коэффициент наклона зубьев для прямозубых передач ![]() , для косозубых определяется по зависимости
, для косозубых определяется по зависимости
![]() , (14.32)
, (14.32)
при ![]()
![]() .
.
Коэффициент неравномерности распределения нагрузки для прямозубых передач принят ![]() , а для косозубых коэффициент
, а для косозубых коэффициент ![]() определяются по графикам на рис.87. Коэффициент динамической нагрузки
определяются по графикам на рис.87. Коэффициент динамической нагрузки ![]() определяют по таблице 14.4
определяют по таблице 14.4
Таблица 14.4 Значения коэффициента динамических нагрузок ![]()
|
Степень точности |
Твердость поверхностей зубьев |
υ, м/с |
|||||
|
1 |
2 |
4 |
6 |
8 |
10 |
||
|
6-я |
а |
||||||
|
б |
|||||||
|
7-я |
а |
|
|||||
|
б |
|||||||
|
8-я |
а |
||||||
|
б |
|||||||
|
9-я |
а |
||||||
|
б |
Примечания: 1. Твердость поверхности зубьев: а) ![]() и
и ![]() или
или ![]() и
и ![]() ; б)
; б) ![]() и
и ![]() . 2. 3начения
. 2. 3начения ![]() в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.
в числителе относятся к прямозубым передачам, а в знаменателе – к косозубым.
Если материал зубчатых колес одинаковый, то расчет зубьев на изгиб производят по шестерне, у которой толщина зубьев у основания меньше и соответственно коэффициент формы зубьев YF больше, чем у зубьев колеса. Если материал зубьев шестерни более прочный по сравнению с материалом зубьев колеса, что обычно и принимается, то расчет зубьев на изгиб нужно производить по тому зубчатому колесу, для которого отношение ![]() имеет меньшее значение. Рекомендуется материал зубьев шестерни и колеса принимать таким, чтобы отношение
имеет меньшее значение. Рекомендуется материал зубьев шестерни и колеса принимать таким, чтобы отношение ![]() для обоих зубчатых колес было примерно одинаковым.
для обоих зубчатых колес было примерно одинаковым.
Если известно напряжение изгиба для зуба шестерни, то для зуба колеса условие прочности на изгиб запишется в виде
![]() . (14.33)
. (14.33)
При действии кратковременных перегрузок зубья проверяют на пластическую деформацию или хрупкий излом при изгибе от максимальной нагрузки:
![]() , (14.34)
, (14.34)
где ![]() – максимальное расчетное напряжение на изгиб в зубьях при их перегрузке максимальным моментом
– максимальное расчетное напряжение на изгиб в зубьях при их перегрузке максимальным моментом ![]() ;
; ![]() – допускаемое максимальное напряжение на изгиб для зубьев;
– допускаемое максимальное напряжение на изгиб для зубьев; ![]() – расчетное напряжение на изгиб для зубьев, вызываемое расчетным моментом
– расчетное напряжение на изгиб для зубьев, вызываемое расчетным моментом ![]() и определяемое по формуле (14.31).
и определяемое по формуле (14.31).
Значение допускаемых максимальных напряжений
на изгиб для зубьев ![]() принимают: при твердости поверхности зубьев
принимают: при твердости поверхности зубьев ![]()
![]() , где
, где ![]() – предел текучести материала зубьев при растяжении; при твердости
– предел текучести материала зубьев при растяжении; при твердости ![]()
![]() , где
, где ![]() – предел прочности материала зубьев при растяжении. Расчет зубьев по формуле (14.34) производят для менее прочного колеса передачи.
– предел прочности материала зубьев при растяжении. Расчет зубьев по формуле (14.34) производят для менее прочного колеса передачи.
Задача 14.1. Выполнить расчет зубчатой передачи. Выполнить проектный и проверочный расчеты (на контактную и изгибную прочность) косозубой зубчатой передачи быстроходной ступени двухступенчатого цилиндрического редуктора. Параметры циклограммы нагружения шестерни: момент на шестерне ![]() , продолжительность работы
, продолжительность работы ![]() ;
; ![]() ,
, ![]() ;
; ![]() ,
, ![]() . Частота вращения шестерни
. Частота вращения шестерни ![]()
![]() . Передаточное число
. Передаточное число ![]() , передача нереверсивная. Марка стали колес – сталь 40ХН. Способ упрочнения – закалка при нагреве ТВЧ до твердости поверхности зубьев
, передача нереверсивная. Марка стали колес – сталь 40ХН. Способ упрочнения – закалка при нагреве ТВЧ до твердости поверхности зубьев ![]() .
.
Решение. Проектный расчет зубчатой передачи.
Принимаем коэффициент ширины по межосевому расстоянию из стандартного ряда значений ![]() .
.
Коэффициент ширины по диаметру шестерни по формуле (14.8)
![]() .
.
Ориентировочное значение коэффициента неравномерности распределения нагрузки ![]() определяем по рис.84. Твердость зубьев
определяем по рис.84. Твердость зубьев ![]() соответствует твердости
соответствует твердости ![]() , согласно зависимостям на рис.88. Для схемы ІІ, при твердости зубьев
, согласно зависимостям на рис.88. Для схемы ІІ, при твердости зубьев ![]() (рис.84.):
(рис.84.): ![]() .
.
Предел контактной выносливости поверхностей зубьев, соответствующий базовому числу циклов напряжений ![]() определяем по таблице 14.1.
определяем по таблице 14.1.
![]() =
=![]()

Рис.88. Зависимости для определения твердости в единицах
Коэффициент запаса прочности ![]() .
.
Базовое число нагружений для материала шестерни и колеса по формуле (14.16)
![]()
![]()
Эквивалентное число циклов нагружений зубьев шестерни при работе передачи с переменными нагрузками по зависимости (14.19) с учетом того, что частота вращения на всех режимах одинакова и равна ![]() . (При постоянном нагружении эквивалентное число циклов определяется по зависимости (14.18))
. (При постоянном нагружении эквивалентное число циклов определяется по зависимости (14.18))
![]() =
=
=![]() =
=
=![]() циклов.
циклов.
Эквивалентное число нагружений зубьев колеса
![]() циклов.
циклов.
Коэффициенты долговечности для зубьев шестерни и колеса по формуле (14.17)
 ,
,
 .
.
Допустимые контактные напряжения по формуле (14.15), с учетом ![]()
– для шестерни
![]() ;
;
– для колеса
![]() .
.
Так как твердость поверхности зубьев шестерни и колеса одинаковы, то в качестве расчетного допускаемого контактного напряжения принимаем меньшее значение
![]() .
.
Расчетное межосевое расстояние определяем по формуле (14.14) для косозубой передачи
 .
.
Принимаем наибольшее значение из стандартного ряда ![]() .
.
Находим предел усталости зубьев при изгибе по табл. 14.2. для стали 40ХН с упрочнением ТВЧ ![]() .
.
Базовое число циклов нагружений зубьев изгибом ![]() .
.
Эквивалентное число циклов нагружений изгибом зубьев шестерни при работе передачи с переменными нагрузками по зависимости (14.26) с учетом (14.24) и того, что частота вращения на всех режимах одинакова и равна ![]() :
:
![]() =
=
=![]()
=![]() циклов.
циклов.
Для зубьев колеса эквивалентное число циклов нагружений изгибом
![]() циклов.
циклов.
Коэффициенты долговечности для зубьев шестерни и колеса на изгиб с учетом того, что ![]() и
и ![]() , то
, то ![]() .
.
Допускаемое напряжение на изгиб для зубьев шестерни определим по формуле (14.23) при ![]() и
и ![]()
![]() .
.
Предварительно принимаем коэффициент формы зуба шестерни ![]() .
.
Расчетная ширина венца зубчатого колеса
![]() .
.
Принимаем стандартный размер ширина венца ![]() .
.
Ширина зубчатого венца шестерни ![]() .
.
Принимаем ![]() .
.
По известному значению межосевого расстояния ориентировочно определяем модуль зацепления по зависимости (14.27) для косозубой передачи
![]() мм.
мм.
Принимаем стандартное значение модуля зацепления ![]() мм.
мм.
Предварительное значение угла наклона зубьев принимаем из диапазона ![]() . Принимаем
. Принимаем ![]() .
.
Число зубьев шестерни по межосевому расстоянию и модулю определим по зависимости:
![]()
![]() .
.
Принимаем число зубьев шестерни ![]() .
.
Число зубьев колеса
![]() .
.
Уточнение угла наклона зубьев по межосевому расстоянию и числу зубьев
![]()
![]() 0,96 и
0,96 и ![]() .
.
Принимаем коэффициент коррекции при изготовлении зубьев ![]() .
.
Расчет геометрических, кинематических и силовых параметров для выполнения проверочных расчетов.
Делительные диаметры колес зацепления:
– шестерни ![]()
![]() 166,67мм;
166,67мм;
– колеса ![]()
![]() 333,33мм.
333,33мм.
Начальные диаметры:
– шестерни ![]()
![]() 166,67мм;
166,67мм;
– колеса ![]()
![]() 333,33мм.
333,33мм.
Диаметр вершин зубьев:
– шестерни ![]() 176,67мм,
176,67мм,
– колеса ![]() 343,33мм.
343,33мм.
Диаметр впадин зубьев:
– шестерни ![]() 154,17мм,
154,17мм,
– колеса ![]() 320,83мм.
320,83мм.
Делительный угол профиля зуба в торцевом сечении
 =
=  20,760.
20,760.
Угол зацепления передачи при ![]()
![]() .
.
Коэффициент торцевого перекрытия:
 =
=
![]() =1,66.
=1,66.
Коэффициент осевого перекрытия
![]() =
=![]() 1,12.
1,12.
Окружная скорость
![]()
Принимаем при такой скорости 8-ую степень точности (табл.14.5) с шероховатостью поверхности зубьев ![]() мкм.
мкм.
Таблица 14.5 Степени точности зубчатых передач
|
Степень точности |
Окружная скорость колес, м/с, не более |
Область применения |
|
|
прямозубых |
косозубых |
||
|
6 – я |
15 |
30 |
Скоростные передачи, делительные механизмы |
|
7 – я |
10 |
15 |
Передачи при повышенных скоростях и умеренных нагрузках или наоборот |
|
8 – я |
6 |
10 |
Передачи общего машиностроения, не требующие особой точности |
|
9 – я |
2 |
4 |
Тихоходные передачи с пониженными требованиями к точности |
Проверочные расчеты зубчатого зацепления на контактную прочность зубьев.
Определяем по графику на рис.87. а коэффициент неравномерности распределения нагрузки ![]() в зависимости от скорости и 8-ой степени точности изготовления
в зависимости от скорости и 8-ой степени точности изготовления ![]()
Определяем по таблице 14.3 коэффициент динамической нагрузки ![]() для твердости поверхности зубьев
для твердости поверхности зубьев ![]() при скорости
при скорости ![]() и 8-ой степени точности изготовления
и 8-ой степени точности изготовления ![]() =1,045.
=1,045.
Коэффициент неравномерности
![]()
![]() 1,26.
1,26.
Расчет зубьев на контактную прочность выполняем по зависимости (14.29)
![]()
Следовательно, условие контактной прочности зубьев выполнено. Допускается превышение ![]() над
над ![]() до 5%.
до 5%.
Проверочный расчет на изгибную прочность зубьев. Определяем по графику на рис.87 а коэффициент неравномерности распределения нагрузки на изгиб ![]() в зависимости от скорости и 8-ой степени точности изготовления
в зависимости от скорости и 8-ой степени точности изготовления ![]() .
.
Определяем по графику на рис.86 б коэффициент неравномерности распределения по длине контактных линий на изгиб ![]() в зависимости от схемы зацепления и твердости зубьев
в зависимости от схемы зацепления и твердости зубьев ![]() .
.
Определяем по таблице 14.3 коэффициент динамической нагрузки на изгиб ![]() для твердости поверхности зубьев
для твердости поверхности зубьев ![]() при скорости
при скорости ![]() и 8-ой степени точности изготовления
и 8-ой степени точности изготовления ![]() =1,07.
=1,07.
Эквивалентное число зубьев косозубой передачи определяем по формуле (14.22)
– для шестерни ![]() ,
,
– для колеса ![]() .
.
Коэффициент формы зубьев колес принимаем по графику рис.85. в зависимости от эквивалентного числа зубьев:
– для шестерни ![]() 3,75,
3,75,
– для колеса ![]() 3,62.
3,62.
Коэффициент учитывающий угол наклона зубьев определяем по формуле (14.32)
![]() =
=![]() =0,88.
=0,88.
Коэффициент, учитывающий перекрытие зубьев передачи
![]() =
=![]() 0,6.
0,6.
Окружную силу в зацеплении определим по формуле (14.10)
![]() =
= ![]() 25200Н.
25200Н.
Расчетные напряжения изгиба в зубьях
– для шестерни
![]()
![]() ,
,
– для колеса
![]()
![]() .
.
Следовательно, условие прочности зубьев на изгиб обеспечивается.
Задача 14.2. Определить размеры открытой конической зубчатой передачи. Передаваемая мощность N=3,5·103Вт. Передаточное числа i = 4.Частота вращения ведущего вала ![]() Передача нереверсивная.
Передача нереверсивная.
Решение. Углы при вершинах начальных конусов
![]()
![]()
Выбираем материал зубчатых колес. Материал шестерни – сталь Ст.5, материал колеса – чугун СЧ 21–40 т. к. передача открытая расчет будет производится только из условия прочности зубьев на изгиб.
Допускаемые напряжения изгиба для шестерни
![]()
где ![]() ;
;
для колеса
![]()
где![]() – предел прочности чугуна СЧ 21-40 на растяжение.
– предел прочности чугуна СЧ 21-40 на растяжение.
Задаемся числом зубьев шестерни ![]() Тогда
Тогда
![]()
![]()
![]()
Сравнительная прочность зубьев шестерни и колеса на изгиб:
для шестерни
![]()
для колеса
![]()
Таким образом, расчет следует вести по колесу.
Задаемся: ![]()
![]()
![]() Расчетный момент на ведущем валу
Расчетный момент на ведущем валу
![]()
Здесь принято предварительно K=1,5.
Момент расчетный на ведомом валу (валу колеса) без учета потерь в зацеплении и подшипниках
![]()
Максимальный модуль зацепления при коэффициенте износа γ = 1,2


Принимаем ![]() из ряда стандартных значений модулей (по ГОСТ 9563-80).
из ряда стандартных значений модулей (по ГОСТ 9563-80).
По найденному ![]() определяем размеры колес:
определяем размеры колес:
![]()
![]()
![]()
![]()
![]()
Углы конусов выступов
![]()
![]()
![]()
Тогда
![]()
![]() .
.
Длина зуба
![]()
Средний модуль
![]()
Важные замечания.
Смещение исходного контура при нарезке зубьев применяют для восстановления изношенных поверхностей зубьев колеса, уменьшения глубины врезания на валах-шестернях, для увеличения нагрузочной способности зубчатой передачи, для выполнения передачи с заданным межосевым расстоянием не равным делительному расстоянию, для устранения подрезания ножек зубьев шестерни и головок зубьев колеса с внутренними зубьями.
Смещение производящего контура на практике применяют обычно при изготовлении прямозубых колес и очень редко косозубых.
Это обусловлено тем, что по изгибной прочности косой зуб прочнее прямого, а необходимое межосевое расстояние можно обеспечить соответствующим углом наклона зубьев. Если высотную коррекцию изредка применяют для косозубых передач, то угловую практически никогда.
Косозубая передача работает более плавно и бесшумно, чем прямозубая. Как уже было сказано, косые зубья имеют более высокую прочность на изгиб и заданное межосевое расстояние можно обеспечить углом наклона зубьев и не прибегать к смещению производящего контура. Однако в передачах с косыми зубьями появляются дополнительные осевые нагрузки на подшипники валов, а диаметры колес имеют больший размер, чем прямозубые при том же числе зубьев и модуле. Косозубые колеса менее технологичны в изготовлении, особенно колеса с внутренними зубьями.
Подписывайтесь
на анонсы статей в окнах, расположенных в конце каждой статьи или вверху каждой страницы.
Ссылка на скачивание файла: modul-zubchatogo-kolesa (xls 41,0KB).
Расчёт диаметра шестерни.
Сегодня рассмотрим как рассчитать диаметр шестерни. Сразу скажу что диаметр прямозубой шестерни имеет одну формулу, а диаметр косозубой шестерни имеет другую формулу. Хотя многие считают по одной формуле, это ошибочно. Данные расчёты нужны для других расчётах при изготовлении зубчатых колёс. Итак перейдём непосредственно к формулам (без коррекции):
Для начала значения которые надо знать при расчётах в данных формулах:
- De — диаметр окружности выступов.
- Dd — диаметр делительной окружности (непосредственно от шага которой считается модуль шестерни).
- Di — диаметр окружности впадин.
- Z — число зубьев шестерни.
- Z1 — число зубьев шестерни малого колеса.
- Z2 — число зубьев шестерни большого колеса.
- M (Mn) — модуль (модуль нормальный, по делительному диаметру).
- Ms — модуль торцевой.
- β (βd) — угол наклона шестерни (иметься ввиду угол наклона по делительному диаметру).
- Cos βd — косинус угла на делительном диаметре.
- A — межцентровое расстояние.
Диаметры окружностей
Рассмотрение геометрии зубчатых пар невозможно без определения диаметров. На каждой детали их выделяется несколько. Широкое распространение имеет диаметр окружности по выступам, иногда называемый диаметром вершин. Он определяет максимальные габариты диска колеса. Его противоположностью считается диаметр окружности впадин. Разность этих величин, поделенная пополам, дает полную длину зуба. Но этот параметр в чистом виде не используется. При расчетах принято выделять высоту головки и ножки зуба. Граница, отделяющая два этих понятия, называется делительной окружностью зубчатого колеса. Диаметр данной окружности выполняет функцию опорного параметра при выполнении расчетов геометрии, так как именно по ней определяется окружной шаг и модуль зацепления. Еще один диаметральный параметр, называемый основной окружностью, описывает теоретическую кривую, которая является базой при построении эвольвенты. Диаметр основной окружности используется для построения конкретного профиля зуба.

Геометрический расчёт зубчатых колёс
В результате геометрического расчета прямозубых цилиндрических колес (без смещения) определим следующие их параметры (рисунок 2): межосевое расстояние , модуль зубьев m, числа зубьев шестерни z1 и колеса z2, делительные диаметры шестерни и колеса , диаметры окружности вершин и , диаметры окружности впадин и , ширина венцов колеса и шестерни .

Рисунок 2 — Параметры цилиндрических колес
1) Рассчитаем предварительно межосевое расстояние, выбрав коэффициент ширины колеса =0,4; полагая, что пара расположена симметрично опорам:
,
где Ка – коэффициент, для прямозубой передачи Ка = 495 МПа 1/3 ;
u – передаточное число редуктора, u = ……;
T2 – вращающий момент на валу колеса, T2 = …. Н·м;
[σH
] — допускаемое контактное напряжение, [
σH
] = 491 МПа;
– коэффициент ширины венца зубчатого колеса, рекомендуемые значения = 0,4;
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
Скачать ГОСТ 9563-60
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
m=t/π,
где t — шаг.

Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
m=h/2,25,
где h — высота зубца.
И, наконец,
m=De/(z+2),
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Основные параметры
Для обеспечения подвижности и работоспособности, конструкция отдельных деталей механической передачи должна быть согласована по размерам и геометрии. Для этого при описании подобных устройств принято использовать систему специальных параметров. В их число входят геометрические, массогабаритные и прочностные величины, закрепленные стандартами. Применение стандартных параметров позволяет сравнительно просто производить расчет унифицированных зубчатых передач и обеспечивает гарантированное сопряжение всех изделий между собой. Естественно, что для разных видов, параметры будут несколько отличаться. Далее рассматриваются термины, связанные с конструкцией эвольвентного цилиндрического колеса. Эти параметры, в своем большинстве, описывают основные характеристики и других вариантов колес.
В основе сечения зуба большинства шестерен лежит эвольвентный профиль, который получается на основе одноименной кривой. Его применение легко стандартизируется, характеризуется высокой технологичностью изготовления и низкими требованиями к качеству сборки механизма. Основными параметры эвольвентного зубчатого колеса считаются модуль зацепления и количество зубьев зубчатого колеса. При одном и том же наружном диаметре деталей значения этих величин могут существенно отличаться в разных вариантах конструкции.
Число зубьев определяет коэффициент передачи и геометрические размеры зубьев. На ведущем колесе редуктора оно выполняется меньшим, чем на ведомом. В итоге один нормальный оборот ведущей шестерни приводит к повороту ведомого колеса только на определенный угол. Отношение числа зубьев двух колес дает значение передаточного коэффициента. Размеры зубьев определяются как отношение их количества к длине окружности колеса. С целью упрощения расчетов и гарантированного обеспечения зацепления между разными колесами, предусмотрен дополнительный параметр, называемый модулем зацепления. Любые шестерни с одинаковым модулем обеспечивают взаимодействие между собой и могут использоваться для построения механизмов, без дополнительной обработки.
Сумма ширины зуба и впадины совместно дают шаг зубчатого колеса. Учитывая неравномерность профиля по радиусу и зависимость длины дуги от диаметра, в каждом колесе можно определить бесконечное число значений этого параметра. С целью стандартизации принято рассматривать шаг по делительной окружности, называемый так же окружным шагом. Отношение этого шага к числу пи дает модуль зацепления. В некоторых случаях для описания шестерен используют угловой шаг, измеряемый в градусах. Стандартами предусмотрены и несколько других угловых величин. Например, для упрощения настройки оборудования при изготовлении колес рассматривают угловую ширину зуба и угловую ширину впадины. Определяются они также на основе делительной окружности.
Достоинства и недостатки
Особенностью червячной передачи является наличие тормозящего момента и большой интервал передаточных чисел и крутящего момента. К положительным характеристикам относятся:
- передаточное число в пределах 8–100;
- работает тихо;
- начало вращения и остановка происходят плавно;
- высокая точность перемещений;
- возможность смещения на малую величину;
- компактность узла;
- самотормозящая передача.
Передача движения в паре червяк и червячное колесо возможна только в одном направлении. При попытке ведомой детали провернуться, возникает тормозящий момент. Это используют в приводе поворота и подъемных механизмах.
Основной недостаток в потерях мощности, связанных с большим трением. Это приводит к быстрому износу деталей, особенно колеса. К недостаткам относятся:
- низкий КПД;
- трение;
- сильный нагрев;
- изготовление венца из дорогих материалов;
- частое заедание;
- быстрое изнашивание;
- постоянная регулировка зацепления подтягиванием червяка;
- сложное изготовление.

Червячное зацепление требует высокой точности изготовления винтового зацепления и чистоты обработки. Передача не переносит попадание в рабочую зону пыли и другого мусора. Требует интенсивной смазки и охлаждения.
Расчет передаточного числа червячной передачи
Ведущая деталь, передающая вращение – червяк, не имеет зубьев. На нем нарезается резьба с числом заходов: 1, 2, 4. Червяки с 3 витками ГОСТом не предусмотрены. Их можно рассматривать и рассчитывать только теоретически. При расчете передаточного числа вместо количества зубьев шестерни берется число заходов резьбы.
Рассчитать передаточное число червячной передачи, формула аналогична другим зубчатым зацеплениям:
где U – передаточное число; Z1 – число заходов на червяке; Z2 – количество зубьев на колесе.

Обратная передача крутящего момента от колеса на червячный вал невозможна. Из-за сильного трения зубьев и низкого КПД передачи колесо не может быть ведущим. Это позволяет не делать тормоза в подъемных механизмах. Достаточно регулировать вращение червячного вала.
Расчет передаточного отношения
Величина передаточного отношения червячной передачи рассчитывается по отношению скорости скольжения червяка и вала.
Где V1 – скорость скольжения червяка; V2 – скорость скольжения червячного колеса. Аналогично w1 и w2 угловые скорости; dδ1, dδ2 – диаметры.
Произведя подстановку формул значений скоростей скольжения, и математические сокращения получает формулу передаточного отношения червячной передачи:
Где i – передаточное отношение. В червячном зацеплении оно равно передаточному числу.
Характеристики червячных передач нормируются по ГОСТ 2144-76. Для червяка с 1 и 2 заходами передаточное число может иметь значение 8-80. Для 4-заходных червяков разбег значений меньше, в пределах 30-80.
ОБЩИЕ ПОЛОЖЕНИЯ
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Принципиальная схема расчета геометрии приведена на чертеже.
1.2. Термины и обозначения, примененные в настоящем стандарте, соответствуют ГОСТ 16530-83 и ГОСТ 19325-73.
1.3. Наименования параметров, приводимых на рабочих чертежах зубчатых колес, выделены в таблицах настоящего стандарта полужирным шрифтом.
1.4. При отсутствии в обозначениях параметров индексов «1» и «2», относящихся соответственно к шестерне и колесу, имеется в виду любое зубчатое колесо передачи.
1.5. При отсутствии дополнительных указаний везде, где упоминается профиль зуба, имеется в виду внешний торцовый профиль.
1.6. Расчетом определяются номинальные размеры зубчатой передачи и зубчатых колес.
1.7. Вычисления по формулам стандарта и приложений к нему, за исключением случаев специально отмеченных, должны производиться со следующей точностью:
линейные размеры — с точностью не ниже 0,0001 мм;
отвлеченные величины — с точностью не ниже 0,0001;
угловые размеры — с точностью не ниже 1′;
тригонометрические величины — с точностью не ниже 0,00001;
передаточные числа, числа зубьев эквивалентных зубчатых колес, коэффициенты смещения и коэффициенты изменения толщины зуба — с точностью не ниже 0,01.
1.8. Пример расчета приведен в справочном приложении 4.
Источник: docs.cntd.ru
Построение эвольвентного зацепления
Существует несколько способов построения эвольвентного зацепления, используемого для изготовления зубчатых колес, которые можно выполнять вручную или с помощью систем автоматического построения.
При проектировании зацепления зубчатых колес учитывают не только геометрические параметры, но и технологические процесс изготовления, а также желаемые динамические и прочностные показатели готового механизма.

Построение эвольвенты зубчатого колеса состоит из нескольких этапов:
- Графическое построение окружности радиусов (определяется исходя из необходимого количества зубьев и прочностных характеристик готового механизма).
- Через полюс зацепления проводится прямая в токе касания изначальных окружностей (строится под необходимым углом зацепления).
- Окружности колес должны соприкасается по полученной прямой. Обкатывание ее по окружности первого колеса, точка, совпадающая с полюсом, образует первую эвольвенту. Такая же манипуляция с колесом 2, позволяет получить вторую эвольвенту.
При производстве шестерен зубья несколькими методами: копирования и обкатки. Если необходимо изготовить мелкую деталь, прибегают к методу формообразования, другими словами – горячей накатки. Такой способ менее точен, но форма фрезы при копировании не позволяет выполнить миниатюрные вырезы.
Метод копирования предусматривает вращение фрезы вдоль поверхности, образующее зубья. Она прорезает одну впадину за один проход между соседними зубьями. Затем фреза возвращается в базовое положение с одновременным поворотом заготовки на необходимый угол шага. Такой способ изготовления довольно точный, но производительность его низкая.

Более совершенным способом является метод обкатки. В его основе лежит огибающее движение, соответствующее желаемому движению зубчатого колеса при зацеплении. Процесс производства похож на движение шестерен в работе. Такое зацепление называется станочным. Рабочий инструмент в таком случае изготавливается в виде круглой, зубчатой фрезы или инструментной рейки.
Подготовка чертежей
Процесс изготовления начинается с непосредственной подготовки чертежа. В этом случае производство существенно упрощается, существенно повышается точность получаемого изделия. При разработке чертежа указывается следующая информация:
- Диаметр посадочного отверстия. Для шестерен изготавливаются соответствующие валы, которые имеют определенный посадочный диаметр. Этот показатель стандартизирован, выбирается в зависимости от размеров изделия и величины предаваемого усилия.
- Размеры шпонки. Шпоночное отверстие может быть самым различным, размеры выбираются в зависимости от того, какие будут оказываться нагрузки. Стоит учитывать тот момент, что размеры шпонок стандартизированы.
- Модуль. Этот параметр считается наиболее важным, так как ошибочный модуль может снизить эксплуатационные характеристики механизма.
- Наружный и внутренний диаметр, определяющие размер зуба. Стоит учитывать, что этот элемент изделия характеризуется достаточно большим количеством особенностей.
- Угол расположения зуба относительно оси вращения. Выделяют шестерни с прямым и косым расположением зуба.
Изготовление шестерен любых размеров возможно только при применении специальных станков, которые предназначены для решения поставленной задачи.
Технологические задачи при производстве рассматриваемого изделия могут существенно отличаться. Важными моментами можно назвать следующее:
- Точность размеров. Наиболее точными размерами обладает отверстие, которое выступает в качестве посадочного для вала. В большинстве случаев его изготавливают по 7-му квалитету в случае, если к изделию не предъявляются больше требования.
- Точность формы. В большинстве случаев при изготовлении шестерен особые требования к точности формы не предъявляются. Однако, посадочное отверстие должно быть расположено в центральной части изделия, так как даже несущественно смещение может привести к отсутствию возможности использования изделия.
- Точность взаимного расположения. Больше всего требований предъявляется к тому, каким образом зубья и другие конструктивные элементы расположены относительно друг друга. При нарушении геометрической формы есть вероятность появления эффекта биения и других проблем при эксплуатации изделия.
- Твердость рабочей поверхности. Основные требования связаны с твердостью рабочей поверхности. Шестерни постоянно находятся в контакте, сила трения может стать причиной быстрого износа поверхности. Для получения требуемого показателя твердости проводится термическая обработка. Рекомендуемый показатель составляет HRC 45…60 при глубине цементации 1-2 мм. Как показывают проведенные исследования, твердость незакаленной поверхности составляет HB 180-270.
- Выбор подходящего материала также имеет значение. В зависимости от области применения изделия они могут изготавливаться из углеродистых, легированных сталей и пластмассы, в некоторых случаях чугуна. Легированные в сравнении с углеродистыми характеризуются большей прокаливаемостью, а также меньшей склонностью к деформации. Применяемые материал должен характеризоваться однородной структурой, за счет чего существенно повышается прочность после проведения термической обработки. При изготовлении высокоточных изделий проводится чередование механической и термической обработки.
Все основные параметры определяются на момент создания технологической карты. Самостоятельно создать карту достаточно сложно, так как для этого нужно обладать соответствующими навыками и знаниями.
Pascal | Лекция №12
Внешние подпрограммы и модули
Содержание:
- Организация внешних подпрограмм
- Создание и использование модулей
- Стандартные модули
Стандартный Паскаль (в отличие от др. языков программирования высокого уровня) не располагает средствами разработки и поддержки библиотек программиста, которые компилируются отдельно и в дальнейшем могут быть использованы не только самим разработчиком. Трудности, связанные с огромными объемами программ, их сложностью и потребностью в коллективной работе, в Турбо Паскале преодолеваются двумя способами:
- введение внешних подпрограмм;
- разработка и использование модулей.
Организация внешних подпрограмм
В этом случае исходный текст каждой процедуры или функции хранится в отдельном файле и при необходимости с помощью специальной директивы компилятора включается в текст создаваемой программы. Внешние подпрограммы в Турбо Паскале сохраняются в файле с расширением inc. Эти файлы можно накапливать на магнитном диске, формируя, таким образом, личную библиотеку подпрограмм.
Пример: дано натуральное число n. Найти сумму первой и последней цифр этого числа.
Для решения используем функцию, вычисляющую количество цифр в записи натурального числа. Сохраним текст этой функции в файле digits.inc:
Function Digits (N: LongInt): Byte; Var Kol: Byte; Begin Kol := 0; While N<>0 Do Begin Kol := Kol+1; N := N Div 10 End; Digits := Kol End;
Опишем еще одну функцию: возведение натурального числа в натуральную степень (an). Сохраним ее в файле power.inc:
Function Power (A,N: LongInt): LongInt; Var I, St: LongInt; Begin St := 1; For I := 1 To N Do St := St * A; Power := St End;
Основная программа, решающая поставленную задачу и использующая описанные выше функции, будет иметь вид:
Program Example1; Var N, S: Integer; {$I digits.inc}{подключение внешней ф-ции из файла digits.inc, вычисляющей кол-во цифр в записи числа} {$I power.inc}{подкл-ие вн. ф-ции из ф. power.inc, вычисляющей рез-т возведения числа A в степень N} Begin Write (?Введите натуральное число:?); ReadLn (N); {для определения последней цифры числа N берется остаток от деления этого числа на 10, а для определения первой цифры N – делится на 10, возведенное в степень на единицу меньшую, чем кол-во цифр в записи числа (т.к. нумерация разрядов начинается с 0)} S := N Mod 10 + N Div Power (10, Digits (N) — 1); WriteLn (?Искомая сумма:?, S) End.
{$I <�имя файла>} – это директива компилятора (псевдокомментарий), позволяющая в данное место текста программы вставить содержимое файла с указанным именем.
Внешние процедуры создаются и внедряются в использующие их программы точно так же, как и функции в рассмотренном примере.
Создание и использование модулей
Далее речь пойдет о модулях: их структуре, разработке, компиляции и использовании.
Модуль – это набор ресурсов (функций, процедур, констант, переменных, типов и т.д.), разрабатываемых и хранимых независимо от использующих программ. В отличие от внешних подпрограмм модуль может содержать достаточно большой набор процедур и функций, а также других ресурсов для разработки программ.
Модуль состоит из следующих частей:
- заголовок модуля;
- интерфейс модуля;
- исполнительная часть модуля;
- раздел инициализации модуля.
Все разделы модуля, за исключением секции инициализации, являются обязательными. Обязательна также указанная последовательность разделов.
Общая схема структуры модуля выглядит следующим образом:
Unit <������������������������������������������������������������������������������������������������
��
��
��головок модуля состоит из зарезервированного слова Unit и идентификатора. Идентификатор модуля должен быть уникальным. Пример заголовка: Unit MyModule;
Модуль должен быть помещен в файл, имя которого совпадает с именем модуля, а его расширение должно быть .PAS.
Через интерфейс осуществляется взаимодействие основной программы с модулем (модуля с модулем). В интерфейсе указываются константы, типы, переменные, процедуры и функции, которые могут быть использованы основной программой (модулем) при вызове этого модуля.
Интерфейсная часть начинается словом Interface. Далее после слова Uses указываются имена модулей, которые используются данным модулем (необязательная часть). После этого могут быть: раздел объявления констант, раздел объявления типов, раздел объявления переменных, раздел объявления процедур и функций. В разделе объявления процедур и функций указываются лишь заголовки подпрограмм. Сами подпрограммы приводятся в исполнительной части.
В интерфейсах различных модулей недопустимо циклическое обращение друг к другу, т. к. компилятор в этом случае не может установить связей.
Исполнительная часть (раздел реализации) включает все подпрограммы модуля. Она может также включать локальные метки, константы, типы и переменные.
Исполнительная часть начинается словом Implementation. Затем после слова Uses указываются имена модулей, которые используются подпрограммами данной исполнительной части (этот раздел необязателен). Если какой-то модуль уже указан в интерфейсе модуля, то в исполнительной части его повторять не следует. Далее могут быть: раздел объявления меток, раздел объявления локальных констант, раздел объявления локальных типов, раздел объявления локальных переменных. Затем идут описания подпрограмм модуля.
В отличие от интерфейсов модулей в исполнительных частях модулей допустимо циклическое обращение друг к другу, т. к. все равно взаимодействие осуществляется через интерфейсы, и здесь не возникает проблемы с установлением необходимых связей.
В некоторых случаях перед обращением к модулю следует провести его инициализацию (например, установить связь с теми или иными файлами с помощью процедуры Assign, инициализировать какие-то переменные и т. д.). Необходимые действия можно вьшолнить в разделе инициализации модуля. Этот раздел начинается словом Begin, после которого идут исполняемые операторы, а затем помещается слово End. (с точкой), например:
Begin Assign(Fl, ‘FILE1.DAT’) End
Следует иметь в виду, что операторы раздела инициализации выполняются единственный раз в момент запуска программы.
Если инициализация модуля не нужна, то в секции помещается лишь слово End. (с точкой).
Пример разработки и использования модуля приведен на стр.147-151 учебника И.Г. Семакин, А.П. Шестаков «Основы программирования».
При разработке модуля рекомендуется такая последовательность действий:
- спроектировать модуль, т.е. определить основные и вспомогательные подпрограммы и ресурсы;
- описать компоненты модуля;
- каждую подпрограмму целесообразно отладить отдельно, после чего «вклеить» в текст модуля.
Разработанный модуль сохраняется в файле с расширением .pas. Для компиляции можно воспользоваться внешним компилятором, поставляемым вместе с Турбо Паскалем. Команда будет выглядеть так: TPC имя_файла.pas. Если в тексте нет синтаксических ошибок, получим файл с расширением .tpu, иначе будет выведено сообщение с указанием строки, содержащей ошибку.
Другой вариант компиляции: в меню системы программирования Турбо Паскаль выбрать Compile/Destination Disk, затем — Compile/Build.
Теперь можно подключить модуль к программе, где планируется его использование.
Стандартные модули
В Турбо Паскале в настоящее время имеется большое количество стандартных подпрограмм, объединенных в несколько стандартных модулей. Они позволяют упростить процедуру написания программ, более полно использовать возможности компьютера, возможности операционной системы. В Турбо Паскале имеются следующие стандартные модули: SYSTEM, STRINGS, CRT, GRAPH, DOS, WINDOS, OVERLAY, PRINTER, TURBO3, GRAPH3. Из них только модуль SYSTEM подключается автоматически к любой программе.
Краткая характеристика модулей:
- модуль SYSTEM включает все стандартные процедуры и функции языка Паскаль и встроенные процедуры и функции языка Турбо Паскаль. Подключается к любой программе автоматически, не требуя объявления;
- модуль STRINGS работает с ASCIIZ-строками (строки, оканчивающиеся символом с кодом 0). Введение таких строк связано с необходимостью совместить программы, написанные в Турбо Паскале, с программами, использующим среду Windows, а также для установления соответствия с др. языками программирования (Си, Ассемблер и т.д.);
- модуль CRT обеспечивает управление текстовым режимом работы экрана (перемещение курсора в любую позицию экрана, изменение цвета символов, фона, управление звуком);
- модуль GRAPH обеспечивает управление графическим режимом работы экрана (позволяет создавать и выводить на экран графические изображения и текстовые надписи);
- модуль DOS отвечает за доступ программ к средствам ОС MSDOS;
- модуль WINDOS следует использовать вместо модуля DOS, когда в программе используются строки, завершающиеся нулями, или когда предполагается в дальнейшем использовать разрабатываемую программу в среде Windows;
- модуль OVERLAY необходим при разработке больших программ, требующих большого количества памяти;
- модуль PRINTER отвечает за вывод текстов на принтер;
- модули TURBO3 и GRAPH3 созданы для совместимости с ранней версией 3.0 системы Турбо Паскаль.
При использовании ресурсов модуля программисту совсем не обязательно иметь представление о том, как работают вызываемые подпрограммы. Достаточно знать назначение подпрограмм и их спецификации (т.е. имена и параметры). По такому принципу осуществляется работа со всеми стандартными модулями.
Контрольные вопросы
- Какими причинами обусловлено использование внешних подпрограмм и модулей?
- Что называется модулем?
- Назовите составные части модуля.
- Какие стандартные модули используются в Турбо Паскале?
- По какому принципу осуществляется работа со стандартными модулями?
Основные параметры зубчатых цилиндрических передач
Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым
Межосевые расстояния
| 1 ряд | 40 | 50 | 63 | 80 | 100 | 125 | — | 160 | — | 200 | — | 250 | — | 315 | — | 400 |
| 2 ряд | — | — | — | — | — | — | 140 | — | 180 | — | 225 | — | 280 | — | 355 | — |
| 1 ряд | — | 500 | — | 630 | — | 800 | — | 1000 | — | 1250 | — | 1600 | — | 2000 | — | 2500 |
| 2 ряд | 450 | — | 560 | — | 710 | — | 900 | — | 1120 | — | 1400 | — | 1800 | — | 2240 | — |
1-й ряд следует предпочитать 2-му
Номинальные передаточные числа
| 1 ряд | 1,0 | — | 1,25 | — | 1,6 | — | 2,0 | — | 2,5 | — | 3,15 | |
| 2 ряд | — | 1,12 | — | 1,4 | — | 1,8 | — | 2,24 | — | 2,8 | — | |
| 1 ряд | — | 4,0 | — | 5,0 | — | 6,3 | — | 8,0 | — | 10 | — | 12,5 |
| 2 ряд | 3,55 | — | 4,5 | — | 5,6 | — | 7,1 | — | 9,0 | — | 11,2 | — |
1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5
Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25
Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636
При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них
Коэффициент запаса прочности при работе зуба двумя сторонами
например: зубья реверсивных передач или зубья сателлитов в планетарных передачах
| Материал колес и термо- обработка | Отливки стальные и чугунные без термо- обработки | Отливки стальные и чугунные с термо- обработкой | Поковки стальные нормали- зованные или улучшенные | Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая) | Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой | Стальные с объемной закалкой | Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др. | Чугунные и пласт- массовые колеса |
| Коэфф. | 1,9 | 1,7 | 1,5 | 2,2 | 1,4 — 1,6 | 1,8 | 1,2 | 1 — 1,2 |
Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 | 1800 | 2000 | 2240 | 2500 |
Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения
| Быстроходная ступень | 40 | 50 | 63 | 80 | 100 | 125 | 140 | 160 | 180 | 200 |
| Промежуточная ступень | 63 | 80 | 100 | 125 | 160 | 200 | 225 | 250 | 280 | 315 |
| Тихоходная ступень | 100 | 125 | 160 | 200 | 250 | 315 | 355 | 400 | 450 | 500 |
| Быстроходная ступень | 225 | 250 | 280 | 315 | 355 | 400 | 450 | 500 | 560 | 630 |
| Промежуточная ступень | 355 | 400 | 450 | 500 | 560 | 630 | 710 | 800 | 900 | 1000 |
| Тихоходная ступень | 560 | 630 | 710 | 800 | 900 | 1000 | 1120 | 1250 | 1400 | 1600 |
Число зубьев шестерни таблица
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ПЕРЕДАЧИ ЗУБЧАТЫЕ КОНИЧЕСКИЕ С ПРЯМЫМИ ЗУБЬЯМИ
Straight bevel gear pairs. Calculation of geometry
Дата введения 1975-01-01
Постановлением Государственного комитета стандартов Совета Министров СССР от 28 марта 1974 г. N 718 срок действия установлен с 01.01.75
ПЕРЕИЗДАНИЕ. Май 1990 г.
Настоящий стандарт распространяется на зубчатые конические передачи с прямыми пропорционально понижающимися зубьями внешнего зацепления с внешним окружным модулем более 1 мм, с межосевыми углами от 10 до 170° и с прямолинейным профилем исходного контура, зубчатые колеса которых нарезаются методом обкатки зубострогальными резцами и парными зуборезными головками, а также методом копирования по шаблону.
Стандарт устанавливает метод расчета геометрических параметров зубчатой передачи, а также геометрических параметров зубчатых колес, приводимых на рабочих чертежах.
Стандарт не распространяется на конические зубчатые передачи с прямыми зубьями кругового профиля.
Применение
Высокие свойства зубчатых передач нашли отражение в широком спектре применений. Во многих промышленных механизмах используются редукторы, призванные понизить число оборотов вращения вала двигателя, для передачи на технологическое оборудование. Помимо изменения скорости, такое устройство также увеличивает механический момент. В итоге маломощный двигатель с большой скоростью вращения, способен приводить в движение медленный и тяжелый механизм.
С целью уменьшения габаритов редуктора его часто выполняют многоступенчатым. Большое количество зубчатых колес входят в последовательное зацепление между собой, обеспечивая высокое передаточное число. Классическим примером подобного устройства являются обычные механические часы. Благодаря множеству специально подобранных передач, скорости движения секундной, минутной и часовой стрелок отличаются друг от друга ровно в 60 раз.
Меняя один комплект на другой, можно получить разные скорости выходного вала. Этот принцип действия лег в основу коробок переключения передач, широко используемых в автомобилестроении, станкостроении и других отраслях.
Обычное зубчатое колесо допускает применение и для повышения скорости выходного вала относительно входного. В общем случае для этого достаточно развернуть редуктор или поменять местами точки подключения двигателя и конечного механизма. Называется подобное устройство мультипликатор. Из особенностей его применения необходимо учитывать запас по мощности двигателя, сопоставимый с передаточным числом механизма.
Зубчатые колеса используются также для изменения направления движения. Две цилиндрические шестерни с одинаковым числом зубьев реализуют функцию смены направления вращения вала. Передачи конической или корончатой конструкции используются в случае необходимости смены положения оси в пространстве. Ведущая и ведомая шестерни в таких механизмах развернуты друг относительно друга на какой-либо угол, значение которого может достигать 90 градусов. При этом передаточное отношение часто равно единице, что обеспечивает одинаковые скорости валов.
Наряду с простыми вариантами передач, содержащих зубчатые колеса, разработаны несколько специальных моделей. С целью снижения материалоемкости, в механизмах с ограниченным углом поворота, используют только часть зубчатого колеса. Такой сектор, обладая всеми основными свойствами зубчатого зацепления, отличается более низкой массой и стоимостью.
Еще один вариант, называемый планетарной передачей, также характеризуется малым весом и габаритами. При этом устройство обеспечивает высокое значение передаточного числа и пониженный уровень шума в процессе работы. Конструктивно такая передача состоит из нескольких шестерен, имеющих разную степень свободы. За счет этого механизм может не только передавать вращение, но и складывать или выделять угловые скорости разных валов, находящихся на одной оси. Сегодня разработано большое число вариантов планетарных передач, отличающихся типом и взаимным расположением зубчатых колес. Планетарные передачи широко применяются в автомобильной и авиационной технике, тяжелом металлорежущем оборудовании. Среди недостатков, сдерживающих распространение передач данного типа, следует отметить низкий КПД и высокие конструктивные требования к точности изготовления отдельных деталей.
Цилиндрические шестерни
Поперечный профиль зуба
Обычно шестерни имеют профиль зубьев с эвольвентной боковой формой. Так как эвольвентное зацепление имеет ряд преимуществ перед остальными: форма этих зубьев соответствует условиям их прочности, зубья легко изготовить и обработать, шестерни не чувствительны к точности установки. Тем не менее, существуют зубчатые передачи с циклоидальной формой профиля зубьев, а так же с шестернями с круговой формой профиля зубьев, например — передача Новикова. Помимо этого, применяется несимметричный профиль зуба, например в храповых механизмах.
Параметры эвольвентной шестерни:
Модуль шестерни (m
) – это основной параметр, который определяется из прочностного расчёта зубчатых передач. Чем сильнее нагрузка на передачу, тем больше значение модуля, единица измерения модуля – миллиметры.
Расчет модуля шестерни:
d
— диаметр делительной окружности
z
— число зубьев шестерни
d
a — диаметр окружности вершин темной шестерни
d
b — диаметр основной окружности — эвольвенты
d
f — диаметр окружности впадин темной шестерни
В машиностроении приняты стандартные значения модуля зубчатого колеса для удобства изготовления и замены зубчатых колёс, представляющие собой числа от 1 до 50.
Высота головки зуба — h
aP и высота ножки зуба —
h
fP в случае, так называемого, «нулевого» зубчатого колеса соотносятся с модулем
m
следующим образом:
h
aP =
m
;
h
fP =
1,2 m
, то есть:
Отсюда получаем, что высота зуба h = 2,2m
Так же можно практически вычислить модуль шестерни, при этом, не имея всех данных для определения модуля, по следующей формуле:
Продольная линия зуба
Прямозубые шестерни
Прямозубые шестерни — самый применяемый тип зубчатых колёс. Зубья расположены в радиальных плоскостях, линия контакта зубьев пары зубчатых колес параллельна оси вращения, как и оси обеих зубчатых колес (шестеренок) располагаются строго параллельно.
Косозубые шестерни
Косозубые шестерни – это модернизированная версия прямозубых шестерен. Зубья, в таком случае, расположены под углом к оси вращения. Зацепление зубьев этих шестерен происходит тише и плавнее, чем у прямозубых. Они применяются либо в малошумных механизмах, либо в тех которые требуют передачи большого крутящего момента на больших скоростях. К недостаткам этого типа шестерен можно отнести: увеличенную площадь соприкосновения зубьев, что вызывает значительное трение и нагрев деталей, а вследствие: потеря мощности и дополнительное использование смазочных материалов; так же механическая сила, направленная вдоль оси шестеренки, вынуждает применять упорные подшипники для установки вала.
Шевронные колёса
Шевронные шестерни решают проблему механической осевой силы, которая возникает в случае применения косозубых колес, так как зубья шевронных (елочных) колёс изготавливаются в виде буквы «V» (или же они образовываются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые механические силы обеих половин шевронной шестерни взаимно компенсируются, поэтому нет нет необходимости использования упорных подшипников для установки валов. Шевронная передача является самоустанавливающейся в осевом направлении, в следствии чего, в редукторах с шевронными колесами один из валов устанавливают на подшипниках с короткими цилиндрическими роликами — плавающих опорах.
Шестерни с внутренним зацеплением
Шестерни такого типа имеют зубья, нарезанные с внутренней стороны. При их использовании происходит одностороннее вращение ведущей и ведомой шестерен. В данной зубчатой передаче меньше затрат на трение, а значит выше КПД. Применяются зубчатые колеса с внутренним зацеплением в ограниченных по габаритам механизмах, в планетарных передачах, в шестеренных насосах, в приводе башни танка.
Винтовые шестерни
Шестерни имеют форму цилиндра с расположенными на нем зубьями по винтовой линии. Эти шестеренки используются на непересекающихся валах, которые располагаются перпендикулярно друг друга, угол между ними 90°.
Секторные шестерни
Секторная шестерня – это часть (сектор) шестерни любого типа, она позволяет сэкономить в габаритах полноценной шестерни, так как применяется в передачах, где не требуется вращение этого зубчатого колеса (шестеренки) на полный оборот.
Шестерни с круговыми зубьями
Шестерни этого типа имеют линию зубьев в виде окружности радиуса, за счет этого контакт в передаче происходит в одной точке на линии зацепления, которая располагается параллельно осям шестерен. Передачи с круговыми зубьями «Передача Новикова» имеет лучшие ходовые качества, чем косозубые – высокую плавность хода и бесшумность, высокую нагрузочную способность зацепления, но при одинаковых условиях их ресурс работы и КПД ниже, к прочему изготовление этих шестерен значительно сложнее. Поэтому применение таких шестеренок ограниченно.
Классификация
По направлению витка передачи в большинстве своем бывают правыми. Иногда встречается левое направление нити.
Червячные зацепления классифицируются по форме наружной поверхности червяка:
- цилиндрические;
- глобоидные.
Вогнутая поверхность ведущей детали увеличивает количество зубьев, находящихся одновременно в зацеплении. В результате возрастает КПД и мощность передачи. Недостаток глобоидных червяков в сложности изготовления. Витки должны быть одинаковой высоты при вогнутой наружной поверхности.
По форме нити резьбы различают червяки:
- архимедов;
- конволютный;
- нелинейный.

Архимедов червяк отличается прямой в сечении эвольвентой. У конволютного конфигурация выпуклая, близкая к форме обычной шестерни. Нелинейные профили имеют выпуклую и вогнутую поверхность.
Зубчатое колесо имеет зуб наклонный обратной конфигурации, по форме совпадающий с впадиной между нитями.
Расположение червяка относительно колеса может быть:
- верхнее;
- боковое;
- нижнее.
Верхнее оптимально подходит для скоростных передач. Боковое наиболее компактное. При картерном способе смазки – масло находится в поддоне и нижняя деталь, вращаясь, смазывает остальные, удобнее нижнее расположение червяка.
Червячные колеса относятся к косозубым. Оси деталей располагаются обычно под углом 90°. В сильно нагруженных механизмах угол может быть 45°.
Зубчатые колеса по профилю зуба делят:
- роликовые;
- вогнутые;
- прямые.
По типу они могут быть:
- с непрерывным вращением – полные;
- зубчатый сектор.
Сектор может быть разной величины, от половины круга, до рабочей длины короче червяка.
Конструкция
Червячная передача получила свое название по ведущей детали, передающей крутящий момент. Ведомая деталь имеет зуб с косой нарезкой. По ободу радиальное занижение поверхности. Это увеличивает линию контакта нити резьбы и зуба.
Оси вращение деталей располагаются под углом. Обычно это 90°, но может быть 45°. Применяется такое расположение деталей в сильно нагруженных тихоходных передачах, со скоростью движения точки на наружной поверхности менее 5 м/сек.
При взаимодействии передачи поверхность резьбы не толкает зубья в направлении вращения, а скользит по эвольвенте, как бы отодвигая ее. В результате возникает сильное трение и нагрев деталей в месте контакта.
Червячная пара должна хорошо смазываться, охлаждаться и обладать антифрикционными свойствами. Материал червяка изменять нельзя, он нарезается из хромистой стали и проходит закалку, шлифовку поверхности резьбы или шугаровку – обработку пластиной с малой глубиной реза. Инструмент скорее продавливает поверхность резьбы, чем режет ее. Создается на верхнем слое наклеп, упрочняющий рабочую поверхность, делающий ее гладкой.
Материал для венца
Венец зубчатого колеса выполняется из относительно мягкого материала с высоким сопротивлением стиранию. В основном применяются оловянные бронзы и латунь. Для низкоскоростных передач с ручным управлением можно делать венец из серого чугуна. В зависимости от скорости вращения зубчатый венец изготавливается из материала:
- 5 – 25 м/сек – оловянистые бронзы ОФ10-1, ОНФ;
- ≤ 5 м/сек – Бр.АЖ9-4, алюминиево-железистая бронза;
- ≤ 2 м/сек – венец может быть из чугуна.
Бронза стоит значительно дороже стали и мягче. Полностью из нее делаются детали, размеры которых в пределах 160 мм. Большие детали вытачиваются из стали и бронзовый на них только венец. Он нагорячо сажается на вал и закрепляется штифтами по линии соединения, чтобы венец не прокручивался. После остывания производится чистовая обработка колеса и нарезается зуб.
Расчет диаметра
Диаметр колеса рассчитывается по средней линии зуба – ширины зуба и впадины равны. Наружный, используемый для изготовления и расчетов радиус, определяется теоретически. После завершения обработки, он находится за пределами фактического обода колеса.
Скольжение происходит по линии делительного диаметра – середина зуба по высоте. Он рассчитывается по формуле:
где d2 — делительный диаметр шестерни; m – модуль; z2 – количество зубьев колеса.
Наружный радиус зуба имеет один центр с осью червяка.
Ширина зубчатого венца
Ширину венца червячного колеса определяют по числу витков винта по формуле:
где b2 – ширина венца; 0,315 и 0,355 – расчетный коэффициент; Z1 – количество заходов винтовой резьбы; a – межцентровое расстояние; aw – расстояние с учетом смещения червяка относительно зубчатого колеса.
Расстояние смещения определяет размер зазора между рабочими элементами деталей.
Технологический процесс
Процесс изготовления шестерни на крупных производственных линиях максимально автоматизирован. Классический техпроцесс характеризуется следующими особенностями:
- Для начала определяются основные параметры изделия, к примеру, число зубьев, модуль и степень точности геометрических размеров.
- Следующий этап заключается в проведении заготовительной процедуры. Чаще всего проводится штамповка при использовании горизонтально-ковочной машины.
- Для повышения эксплуатационных характеристик выполняется нормализация. Подобная термическая обработка позволяет снизить напряжения внутри материала.
- Токарно-винторезная процедура позволяет получить заготовку требующихся размеров. Для этого выполняется точение поверхности и расточка фасок.
- После механической обработки прямозубых шестерен выполняется повторно нормализация.
- Заготовка подвергается зубофрезерной обработке. Для этого применяется полуавтомат 5306К или другое подобное оборудование.
- Следующий шаг заключается в слесарной обработке. Технологический процесс определяет появление заусенец и других дефектов, которые устраняются при применении полуавтомата 5525. На линиях с низкой производительностью зачистка проводится ручным методом.
- После получения зубьев выполняется термическая обработка, для чего часто применяется установка ТВЧ. Закалка позволяет существенно повысить твердость поверхности и ее износостойкость.
- Шлифование поверхности. Для получения поверхности требуемого качества выполняется шлифовка. Есть довольно больше количество различного оборудования, которое подходит для шлифования самых различных поверхностей.
- Большое распространение получили насадные шестерни. Они устанавливаются на валу, могут быть больших и малых размеров. Фиксация насадного варианта исполнения проводится за счет шпонки. Получить шпоночный паз можно при применении долбежного станка.
- Зубошлифование также проводится при применении специальных станков.
https://youtube.com/watch?v=KbjmqvPM-1c
В заключение отметим, что процедура зубофрезервания достаточно сложна, предусматривает применение специального оборудования.
Нарезание червячных колес
При проектировании создается модель червячного колеса. По ней легко определится со способом нарезки:
- заход фрезы снизу;
- торцевой.
Торцевой требует инструмента, в точности повторяющего червяк. Дает хорошую точность и чистоту обработки. Фрезу выставлять сложно, необходимо, чтобы в конце обработки она имела положение относительно колеса, в точности соответствующее червяку.
Нарезка зубьев на венце
По наружному диаметру червячное колесо имеет полукруглое углубление. Это позволяет лучше прилегать деталям по эвольвенте и смещать ось, увеличивая площадь контакта. Центр радиуса углубления должен совпадать с осью червяка.
Фрезы для нарезания червячного колеса должны быть с таким же наружным диаметром, как червяк. Внешне она повторяет форму ведущей детали, только вместо непрерывной линии резьбы ряды резцов. Режущая пластина по форме точно повторяет нитку резьбы, но шире нее на размер зазора. В результате конфигурация ответной детали – червячного колеса, точно повторяет формы резьбы, впадины совпадают с выступами нитей.
Фреза выставляется в плоскости оси червяка, касаясь его поверхности. Зубчатый венец вращается вокруг вертикальной оправки или собственного вала, обеспечивая тангенциальную подачу наружной поверхности относительно оси режущего инструмента. Нарезка червячных колес происходит при синхронном движении инструмента и детали, вращающихся вокруг своих осей. Отношение скорости вращения определяется передаточным числом. С каждым оборотом венец придвигается ближе к вращающейся фрезе.

Подача режущего инструмента возможна снизу и сверху. Но в большинстве случаев используют радиальную нарезку, как наиболее удобную и точную.
![]()
 Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки
Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки

 Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса:
Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса:- d = m × z,
- где z – число зубьев;
- m – модуль.
- Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:
- m = t / π,
- где t – шаг зацепления.
- Высота зуба:
- h = ha + hf,
- где ha – высота головки зуба, ha = m; hf – высота ножки зуба, hf = 1,25m.
- Диаметр окружности выступов зубьев:
- da = d + 2ha = m(z + 2).
- Диаметр окружности впадин:
- df = d – 2hf = m(z – 2,5).

- Служит для передачи вращения при параллельных осях валов.


- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.

- Служит для преобразования вращательного движения в возвратно-поступательное.


- ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для передачи вращательного движения между валами со скрещивающимися осями.
- ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).
- Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …
- Ряд 2: … 1,5; 3; 3,5; 6; 7 …
Примечание. Ряд 1 следует предпочитать ряду 2.
- Служит для передачи вращения при пересекающихся осях валов.
- ГОСТ 9563-60 предусматривает два ряда модулей m= 0,05…100 мм.
- Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …
- Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …
Примечание. Ряд 1 следует предпочитать ряду 2.
Источник: http://dgng.pstu.ru/sprav/8.htm
Зубчатые передачи
 Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Зубчатые передачи — это механизм или часть механизма механической передачи, в состав которого входят зубчатые колёса. Зубчатые передачи служат для того, чтобы непрерывно передавать силу и крутящий момент двух валов, расположение которых определяет тип имеющейся зубчатой передачи. Вот о том, что представляют зубчатые передачи, мы и поговорим в этой статье.
Типы зубчатых передач

Эвольвентное зацепление

Все прямозубые цилиндрические передачи с одинаковым модулем зацепления могут изготавливаться на одном оборудовании, независимо от количества зубьев и размеров головки.
Модули зацепления цилиндрических и конических зубчатых колес стандартизированы по DIN 780; модули зацепления червячных передач по DIN 780; модули шлицевых соединений по DIN 5480; модули зубчатого зацепления нормального профиля для шестерен со спиральными зубьями по DIN 780.
Форма зубьев
 Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Для прямозубых цилиндрических передач форма зубьев определяется DIN 867, DIN 58400; конических передач — DIN 3971; червячных передач — DIN 3975; шлицевых соединений — DIN 5480 (см. рис. «Прямые и косые зубья (наружное зацепление)» ).
Форма зубьев гипоидных передач регламентируется стандартом DIN 867. В дополнение к стандартным углам зацепления (20° для зубчатых передач и 30° для шлицевых соединений) применяются также и углы зацепления 12°, 14°30 15°, 17°30′| 22°30′ и 25°.
Рис. Характеристики прямозубой цилиндрической передачи передачи (циклоидное зацепление)
Коррегирование зубчатого зацепления
 Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Коррегирование зубчатого зацепления (изменение высоты головки зуба (см. рис. «Коррегирование зубчатого зацепления прямозубой цилиндрической передачи (циклоидное зацепление)» ) применяется для предотвращения подрезания у шестерен с малым количеством зубьев. Оно позволяет увеличить прочность ножки зуба и точно обеспечить межосевое расстояние.
Зубчатые передачи с точно заданным межосевым расстоянием
У зубчатых пар с точно заданным межосевым расстоянием изменение высоты головки зуба для шестерни и зубчатого колеса производится на одинаковую величину, но в противоположных направлениях, что позволяет сохранить межосевое расстояние неизменным. Такое решение применяется в гипоидных и косозубых передачах.
Зубчатые передачи с изменяемым межосевым расстоянием
Изменение высоты головки зуба для шестерни и зубчатого колеса производится независимо друг от друга, поэтому межосевое расстояние передачи может изменяться. Допускаемые отклонения линейных размеров зубчатых передач регламентированы. Для прямозубых цилиндрических передач — DIN 3960, DIN 58405; для конических передач — DIN 3971; червячных передач — DIN 3975.
Подставляя jη = 0 в приведенные ниже формулы, рассчитывают параметры зацепления без зазора между зубьями. Для определения зазора между зубьями допускаемые отклонения толщины зубьев и зоны их зацепления принимают в соответствии со стандартами DIN 3967 и DIN 58405 в зависимости от требуемой степени точности зубчатой передачи.
Следует отметить, что не обязательно стремиться к нулевому зазору между зубьями. Для компенсации имеющихся отклонений размеров зубьев и сборки шестерен достаточно иметь минимальный зазор, который, кроме того, предотвращает возможность заклинивания зубчатых колес.
Допускаемые отклонения других расчетных параметров (зазор между ножками двух смежных зубьев, межцентровое расстояние) приведены в стандартах DIN 3963, DIN 58405, DIN 3962 Т2, DIN 3967, DIN 3964.
Расчетные формулы для зубчатых передач

Степени точности зубчатых передач (DIN 3961…..3964)
Зубчатые передачи стартера
Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в силовых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомобильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличением межосевого расстояния.
Модули зубчатых передач стартеров
Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением.
Для шага зубьев принято следующее обозначение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на заготовке, рассчитанной по диаметру на 10 зубьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х.
(Это обозначение нельзя смешивать с обозначением Р 8/10, приведенным ниже).
Стандарты зубчатых передач США
- Вместо модуля для стандартизации зубчатых передач в США используется показатель количества зубьев на 1 дюйм (25,4 мм) диаметра делительной окружности или диаметральный модуль (питч) (Р):
- Р = z/d = z/(z • m/25,4) =25,4/m
- Для перевода стандарта США в европейский стандарт служит зависимость:
- m = 25,4 мм / P
- Размещение зубьев в пределах диаметрального модуля называется окружным шагом зацепления (CP):
- CP = (25,4 мм / P) π.
- Табл. Стандарты зубчатых передач
Полная высота зуба
В стандартах США полная высота зуба обозначается как высота головки ha = т, что соответствует величине т в стандартах Германии.
Ножка зуба
- Обозначается так же, как и полная высота зуба, но расчет головки зуба основывается на использовании своего модуля. Пример обозначения:
- Обозначение (пример): Р 5 /7
- Р = 7 для расчета головки зуба,
- Р = 5 для расчета других параметров.
Система обозначений и преобразований
- Диаметр окружности выступов: OD = da.
- Диаметр делительной окружности: PD = N/P = d (в дюймах) или PD = Nm = d (в мм).
- Диаметр окружности впадин: RD = df
- Начальный диаметр:
- LD =(N+2x) / P (в дюймах)
- или
- LD= (N+2x)·m (в мм).
- LD ≈ dw,
- где dw — диаметральный модуль.
Расчет наибольшего допустимого давления зубчатых передач
Ниже приведены расчетные формулы, которые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способности зубчатых передач». Эти зависимости применимы для расчета нагрузки трансмиссионных зубчатых пар, работающих в стандартном режиме.
Величины и единицы измерения для расчета наибольшего допустимого давления
Необходимое сопротивление усталостному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высокого контактного давления достигается, если величина оценки сопротивления выкрашиванию Sw равна или больше 1.
В случае зубчатого зацепления с z1< 20 следует принимать Sw ⩾ 1,2…1,5 из-за более высоких контактных напряжений в точке однопарного зацепления.
Поскольку контактные давления равны по величине для обоих колес, значение kperm для зубчатого колеса 2 следует принимать такими же, как и для колеса 1 при частоте вращения n2, пользуясь помещаемой ниже таблицей.
Формулы для расчета наибольшего допустимого давления
Содержащиеся в таблице значения коэффициента &Perm применимы, когда оба колеса изготовлены из стали. Для пар зубчатых колес из чугуна и стали или бронзы и стали этот коэффициент следует увеличить в 1,5 раза. В случае зубчатых пар из чугуна по чугуну или бронзы по бронзе коэффициент kperm следует увеличить примерно в 1,8 раза.
Для зубчатого зацепления лишь с одним поверхностно упрочненным колесом, коэффициент kperm для незакаленного колеса необходимо увеличить на 20%. Все приведенные в таблице значения этого коэффициента рассчитаны на срок службы Lh = 5000 ч.
При оценке сопротивления выкрашиванию металла зубчатых колес Sw расчетный срок их службы может изменяться за счет коэффициента срока службы ф.
Коэффициент допустимого контактного давления kperm в H/mm2 для срока службы Lh = 5000 ч
Прочностные характеристики материалов для изготовления зубчатых передач приведены в табл. «Параметры материалов зубчатых передач«.
- При пульсирующей нагрузке для предела усталостной прочности (NL ⩾ 3*106). В случае знакопеременной нагрузки следует применять коэффициент YL
- В пределах усталостной прочности в течение срока службы напряжения изгиба увеличиваются на коэффициент Ynt в зависимости от количества циклов нагрузки NL.
Коэффициент срока службы ф
- Коэффициент срока службы используется для корректирования приведенных в верхней таблице значений коэффициента допустимого контактного давления kperm (рассчитанного на срок службы Lh = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.
- Рекомендации по выбору расчетного срока службы зубчатых передач: при постоянной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной нагрузке — от 50 до 5000 ч.
Необходимая величина сопротивления разрушению зуба обеспечивается при SF ⩾ 1 для шестерни (колесо 1).
Если шестерня изготовлена из более прочного материала, чем зубчатое колесо 2, следует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки.
Расчет зубчатого зацепления на изгиб и разрушение зуба
Коэффициент профиля зуба YFa
Скоростной фактор fv
[1] Оценка действительна для А = 6 (средний уровень точности).
В следующей статье я расскажу об электрических свойствах материалов.
Источник: http://press.ocenin.ru/zubchatye-peredachi/
Примерный расчет элементов зубчатого колеса
Длина всякой окружности равна ΠD; следовательно, длина начальной окружности зубчатого колеса будет выражена формулой Πd,.
Шагом t зацепления называется длина дуги начальной окружности между обращенными в одну сторону (левыми или правыми) профилями двух смежных зубьев см 517, б.
Если размер этой дуги взять столько раз, сколько имеется зубьев у колеса, т. е. z раз, то также получим длину начальной окружности; следовательно,
- Πd = tz отсюда
- d = (t / Π) z
Отношение шага t зацепления к числу Π называется модулем зацепления, который обозначают буквой m, т. е.
t / Π = m
Модуль выражается в миллиметрах. Подставив это обозначение в формулу для d, получим.
- d = mz откуда
- m = d / z
Следовательно, модуль можно назвать длиной, приходящейся по диаметру начальной окружности на один зуб колеса. Диаметр выступов равен диаметру начальной окружности плюс две высоты головки зуба (фиг. 517, б) т.е.
De = d + 2h’
Высоту h’ головки зуба принимают равной модулю, т. е. h’ = m. Выразим через модуль правую часть формулы:
- De = mz + 2m = m (z + 2) следовательно
- m = De : (z +2)
Из фиг. 517,б видно также, что диаметр окружности впадин равен диаметру начальной окружности минус две высоты ножки зуба, т. е.
- Di = d — 2h»
- Высоту h» ножки зуба для цилиндрических зубчатых колес принимают равной 1,25 модуля: h’ = 1,25m. Выразив через модуль правую часть формулы для Di получим
- Di = mz — 2 × 1,25m = mz — 2,5m или
- Di = m (z — 2,5m)
- Вся высота зуба h = h’ + h» т.е
- h = 1m + 1,25m = 2,25m
- Следовательно, высота головки зуба относится к высоте ножки зуба как 1 : 1,25 или как 4 : 5.
Толщину зуба s для необработанных литых зубьев принимают приблизительно равной 1,53m, а для обработанных на станках зубьев (например, фрезерованных) — равной приблизительно половине шага t зацепления, т. е. 1,57m.
Зная, что шаг t зацепления равен толщине s зуба плюс ширина sв впадины (t = s + sв) (Величину шага t определяем по формуле t/Π = m или t = Πm ), заключаем, что ширина впадины для колес с литыми необработанными зубьями.
- sв = 3,14m — 1,53m = 1,61m A для колес с обработанными зубьями.
- sв = 3,14m — 1,57m = 1,57m
Конструктивное оформление остальной части колеса зависит от усилий, которые испытывает колесо во время работы, от формы деталей, соприкасающихся с данным колесом, и др. Подробные расчеты размеров всех элементов зубчатого колеса даются в курсе «Детали машин». Для выполнения графического изображения зубчатых колес можно принять следующие приблизительные соотношения между их элементами:
Толщина обода e = t/2
Диаметр отверстия для вала Dв ≈ 1/в De Диаметр ступицы Dcm = 2Dв Длина зуба (т. е. толщина зубчатого венца колеса) b = (2 ÷ 3) t Толщина диска К = 1/3b Длина ступицы L = 1,5Dв : 2,5Dв
Размеры t1 и b шпоночного паза берутся из таблицы №26. После определения числовых величин модуля зацепления и диаметра отверстия для вала необходимо полученные размеры согласовать с ГОСТ 9563-60 (см таблицу №42) на модули и на нормальные линейные размеры по ГОСТ 6636-60 (таблица №43).
Модули (согласно ГОСТ 9563-60) Таблица №42.

Нормальные линейные размеры. Таблица №43. (Выдержка из ГОСТ 6636-60)

Если они отличаются от табличных значений, надо взять ближайшие большие табличные значения и пересчитать все величины, зависящие от вновь выбранного модуля или диаметра отверстия.
Вычерчивание контура зуба
Источник: http://www.ViktoriaStar.ru/primerni-raschet-elementov-zubchatogo-kolesa.html
Определение основных геометрических параметров зубчатых колес
- Лабораторная работа 10
- Цель работы — ознакомиться с практическими методами определения основных параметров зубчатых колес.
- Краткие теоретические сведения
Основными параметрами зубчатого колеса с эвольвентным профилем зубьев являются: модуль т, число зубьев z, угол зацепления а, величина смещения инструментальной рейки при нарезании зубчатого колеса.
Число зубьев, диаметры окружностей вершин и впадин зубьев можно измерить непосредственно, остальные параметры вычисляют в результате расчета.
Подсчитав число зубьев z, нетрудно определить модуль зацепления, используя свойство эвольвенты: нормаль в любой точке эвольвенты является касательной к основной окружности. Поэтому при охвате нескольких зубьев колеса губками штангенциркуля (размер АВ, рис. 2.5.1) линия АВ будет касательной к основной окружности и нормальной профилям зубьев.
Если отрезок АВ катить по основной окружности, то по свойству эвольвенты точка А придет в точку А0, точка В — в точку В0 и точка D — в точку D0. Тогда
Таким образом, измерив вначале длину общей нормали Wzn (мм), соответствующей числу зубьев z„, а затем размер Wzn+ь охватив губками штангенциркуля на один зуб больше, рь ~ шаг по основной окружности — определим как разность двух измерений:
Это выражение действительно только в том случае, когда губки штангенциркуля касаются эвольвентной части профиля зуба.
Рис. 2.5.1. Схема замера
Чтобы не возникло кромочного контакта, необходимо правильно выбрать zn (табл. 2.5.1).
Таблица 2.5.1
| Число зубьев колеса | 12-18 | 19-27 | 28-36 | 37-45 | 46-54 | 55-63 | 64-72 | 73-81 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Модуль зацепления определим по формуле
Полученное значение модуля сопоставим со стандартным значением (табл. 2.5.2) и примем его ближайшее значение.
Таблица 2.5.2
| т, мм | 2,00 | 2,25 | 2,50 | 2,75 | 3,00 | 3,25 |
| Рь, мм | 5,904 | 6,642 | 7,380 | 8,818 | 8,856 | 9,954 |
| т, мм | 3,50 | 3,75 | 4,00 | 4,50 | 5,00 | 5,50 |
| Рь, мм | 10,33 | 11,07 | 11,808 | 13,28 | 14,76 | 16,84 |
По уточненному значению модуля рассчитаем шаги зацепления по делительной и основной окружностям.
Для определения величины смещения при нарезании зубчатого колеса инструментальной рейкой необходимо измерить толщину зуба по основной окружности, сопоставить результат с расчетным значением той же толщины зуба для колеса, нарезанного без смещения, и найти коэффициент смещения инструментальной рейки:
где sb = Wzn+l — znpb — толщина зуба по основной окружности данного колеса; sb = mcosa(^ + zinva) — толщина зуба по основной окружности зубчатого колеса, нарезанного при х = 0; a = 20°; inv 20° = 0,0149.
При проведении обмера зубчатых колес необходимо измерить также диаметры окружностей выступов da и впадин df.
Если число зубьев шестерни z четное, то оба диаметра могут быть непосредственно измерены штангенциркулем (рис. 2.5.2, а) При нечетном числе зубьев измерение проводится по схеме, изображенной на рис. 2.5.2, б.
Рис. 2.5.2. Определение диаметров при четном (а) и нечетном (б) числе зубьев
Для определения диаметра окружности выступов измеряется диаметр отверстия шестерни ((/0Тв) и размер//’. Тогда диаметр окружности выступов
Аналогично измеряется диаметр окружности впадин:
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
Для проведения этой работы необходимо иметь набор зубчатых колес разных модулей и с разным количеством зубьев и измерительный инструмент — штангенциркуль.
Порядок выполнения работы
- 1. Подсчитать число зубьев колеса z.
- 2. По табл. 2.5.1 определить число зубьев z„, которые следует охватить штангенциркулем.
- 3. Измерить штангенциркулем Wzn и Wzn+ (рис. 2.5.1). Для большей точности обмерять нужно трижды на разных участках зубчатого венца. Окончательные значения Wzn и Wzn+ есть среднеарифметическое трех обмеров. По формуле (2.5.1) определить величину шага рь по основной окружности.
- 4. По формуле (2.5.2) найти модуль зацепления в миллиметрах, округлив его величину до ближайшего стандартного значения согласно табл. 2.5.2. В формуле 2.5.2 угол исходного контура а = 20°.
- 5. Учитывая, что есть колеса с углом а = 15°, выполнить проверочный расчет модуля по выражению
измерив диаметр da окружности вершин.
6. Измерить d/диаметр окружности впадин.
Примечание: da и df при четном числе z измерить штангенциркулем (рис. 2.5.2, а), при нечетном числе — найти в соответствии с рис. 2.5.2, б по формулам:
- 7. Определить:
- а) шаг по делительной окружности
б) диаметр делительной окружности
в) диаметр основной окружности
г) делительную высоту головки зуба
д) делительную высоту ножки зуба
е) коэффициент высоты головки зуба
ж) толщину зуба по основной окружности
- 8. По формуле (2.5.3) рассчитать коэффициент смещения х исходного контура, с которым нарезалось данное колесо.
- 9. Определить толщину зуба по основной окружности:
Контрольные вопросы и задания
- 1. Что такое модуль зубчатого колеса?
- 2. Как определить шаг зубчатого колеса?
- 3. Дайте понятие основной и делительной окружностей.
- 4. Какова зависимость между числом зубьев и диаметром зубчатого колеса?
- 5. Что называется коэффициентом смещения исходного контура?
- 6. Как изменяются основные параметры зубчатого колеса при смещении исходного контура?
Содержание отчёта
- 1. Число зубьев z = …
- 2. Определение шага и модуля зацепления:
| Номер измерения | Wz,,+ь мм | Wzn, мм |
| Среднее |
* число zn выбирается по табл. 2.5.1.
Шаг зацепления по основной окружности pb = WZfJ+1 — Wzn = … мм.
Модуль т = ——— = … мм.
Ttcosoc
Модуль, уточненный по табл. 2.5.2, т = … мм.
Шаг зацепления по делительной окружностир = пт = … мм.
Шаг по основной окружности (уточненный)рь=р cos а= … мм.
- 3. Диаметр делительной окружности d = mz= … мм.
- 4. Диаметр основной окружности db = d cos а= … мм.
- 5. Определение действительной толщины зуба по основной окружности sb = Wzn +1 -znpb = … мм.
- 6. Расчет толщины зуба по основной окружности нулевого колеса:
7. Определение коэффициента смещения:
9. Определение диаметров окружностей вершин da и впадин df колеса:
| Номер измерения | doiB | Н’ | da | Н» | df | Расчётные формулы при нечётном числе z |
| Среднее |
10. Учитывая, что есть колеса с углом зацепления а = 15°, в и. 2 выполнить проверочный расчет модуля по выражению (для нормального колеса)
11. Определение коэффициента высоты головки зуба колеса, зубья которого нарезаны без смещения:
12. Вывод.
Источник: https://studref.com/529843/tehnika/opredelenie_osnovnyh_geometricheskih_parametrov_zubchatyh_koles
Модуль зуба – Модуль шестерни. Формулы расчёта
Шаг зубьев ρ так же, как и длина окружности, включает в себя трансцендентное число π, а потому шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число ρ/π, которое называют модулем зубьев т и измеряют в миллиметрах:
Модулем зубьев т называется часть диаметра делительной окружности, приходящаяся на один зуб. Модуль является основной характеристикой размеров зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым. Для обеспечения взаимозаменяемости зубчатых колес и унификации зуборезного инструмента значения m регламентированы стандартом (табл. 8.1).
Высота головки и ножки зуба. Делительная окружность рассекает зуб по высоте на головку ha и ножку hf. Для создания радиального зазора с (см. рис. 8.19)
Для нормального (некорригированного) зацепления ha = m. Длина активной линии зацепления. При вращении зубчатых колес точка зацепления S (см. рис. 8.9) пары зубьев перемещается по линии зацепления NN.
Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S” пересечения линии зацепления с окружностью вершин шестерни. Отрезок S’S” линии зацепления называется длиной активной линии зацепления и обозначается ga.
Длину ga легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S” и замеряют ga.
Коэффициент торцового перекрытия. Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность передачи.
reductory.ru
Как определить модуль шестерни с прямым и косым зубом
Часто мне задают вопрос: Как определить модуль косозубой шестерни. Один из самых простых вариантов — обкатать фрезой, то есть методом подбора, вставить в шестерню фрезу и посмотреть совпадает ли шаг! Этот вариант подходит для шестернь малого модуля, для более больших шестернь требуются формулы расчёта.
Давайте определим модуль косозубой шестерни. В качестве примера я возьму небольшую шестерню. Данный метод идентичен и для более больших шестернь и больших модулей.
- Есть вот такая шестерня:
- Допустим что фрезы обкатать у нас на данный момент нет и вообще хочется просто посчитать по формуле!
Модуль = De/Z+2. То есть диаметр окружности выступов разделить на количество зубьев плюс 2.
- Измеряем диаметр:
- Диаметр окружности выступов (De) равен 28,6 мм.
- Считаем количество зубьев. Z=25.
- Делительный диаметр (De) делим на количество зубьев 25 +2. Равно 28,6 разделить на 27=1,05925925925926.
- Округляем до ближнего модуля. Получается модуль 1.
- Можно использовать и другой вариант — высота зуба делится на 2,25.
- Я обычно или обкатываю фрезой или считаю по формуле — модуль = De/Z+2.
- Таким образом можно определить модуль как косозубой шестерни, так и шестерни с прямым зубом.
- Поделится, добавить в закладки!
- zuborez.info
Модуль зубчатого колеса – это… Что такое Модуль зубчатого колеса?
Модуль зубчатого колеса геометрический параметр зубчатых колёс.
Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности dд к числу зубьев z или отношению шага t по делительной окружности к числу: m = dд/z = ts/π.
Для косозубых цилиндрических колёс различают: окружной модуль ms = dд/z = ts/π, нормальный модуль mn = tn/π, осевой модуль ma = tа/π, где ts, tn и ta— соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения М. з. к.
стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента (см. Зубчатая передача).
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Модуль высокоэластический
- Модуль расстояния
Смотреть что такое “Модуль зубчатого колеса” в других словарях:
- МОДУЛЬ ЗУБЧАТОГО КОЛЕСА — геометрический параметр, линейная величина, пропорциональная размерам зубчатого колеса. Различают осевой, окружной и нормальный модуль зубчатого колеса … Большой Энциклопедический словарь
- модуль зубчатого колеса — отношение шага зубьев колеса (расстояние между соответствующими точками соседних зубьев, измеренное по дуге окружности) к числу π. Значения модуля зубчатого колеса стандартизованы. Геометрические размеры зубчатых колёс выбираются пропорционально… … Энциклопедический словарь
- нормальный модуль зубьев конического зубчатого колеса — (mn) нормальный модуль Линейная величина, в раз меньшая нормального шага зубьев конического зубчатого колеса. Примечания 1. Различают нормальные модули: внешний (mne), средний (mnm), внутренний (mni) и др. (mnx) делительные; внешний (mnwe),… … Справочник технического переводчика
- нормальный модуль цилиндрического зубчатого колеса — (mn) модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание В случаях, исключающих возможность возникновения недоразумений, индекс… … Справочник технического переводчика
- окружной модуль зубьев конического зубчатого колеса — (mt) окружной модуль Линейная величина, в раз меньшая окружного шага зубьев конического зубчатого колеса. Примечание Различают окружные модули: внешний (mte), средний (mtm), внутренний (mti) и др. (mtx) делительные; внешний (mtwe), средний (mtwm) … Справочник технического переводчика
- расчетный модуль конического зубчатого колеса — расчетный модуль Окружной или нормальный делительный модуль в расчетном сечении. Примечания 1. Расчетный модуль конического зубчатого колеса из семейства сопряженных конических зубчатых колес, форма и размеры зубьев которых определяются парой… … Справочник технического переводчика
- Нормальный модуль цилиндрического зубчатого колеса т n — 2.1.2. Нормальный модуль цилиндрического зубчатого колеса т n Модуль Делительный нормальный модуль зубьев цилиндрического зубчатого колеса, принимаемый в качестве расчетного и равный модулю нормального исходного контура. Примечание. В случаях,… … Словарь-справочник терминов нормативно-технической документации
- Нормальный модуль зубьев конического зубчатого колеса — 67. Нормальный модуль зубьев конического зубчатого колеса Нормальный модуль mn Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
- Окружной модуль зубьев конического зубчатого колеса — 59. Окружной модуль зубьев конического зубчатого колеса Окружной модуль mt Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения … Словарь-справочник терминов нормативно-технической документации
- Расчетный модуль конического зубчатого колеса — 146. Расчетный модуль конического зубчатого колеса Расчетный модуль Источник: ГОСТ 19325 73: Передачи зубчатые конические. Термины, определения и обозначения оригинал документа … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru
Модуль зуба что такое
Модуль зубьев зубчатого колеса
Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня».
За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки.
Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.
Зубчатое колесо
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
Скачать ГОСТ 9563-60
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
- Для расчета этого параметра применяют следующие формулы:
- m=t/π,
- где t — шаг.
- Параметры зубчатых колес
- Модуль зубчатого колеса можно рассчитать и следующим образом:
- m=h/2,25,
- где h — высота зубца.
- И, наконец,
- m=De/(z+2),
- где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
Формула расчета параметров прямозубой передачи
Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
- Расчет модуля зубчатого колеса
- Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:
- π×D=t×z,
- проведя преобразование, получим:
- D=(t /π)×z
Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.
- t/π=m,
- размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:
- В=m×z;
- выполнив преобразование, находим:
- m=D / z.
- Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным
- De=d+2× h’,
- где h’- высота головки.
- Высоту головки приравнивают к m:
- h’=m.
- Проведя математические преобразования с подстановкой, получим:
- De=m×z+2m = m(z+2),
- откуда вытекает:
- m=De/(z+2).
- Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:
- Di=D-2h“,
- где h“- высота ножки зубца.
- Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
- h’ = 1,25m.
- Устройство зубчатого колеса
- Выполнив подстановку в правой части равенства, имеем:
- Di = m×z-2×1,25m = m×z-2,5m;
- что соответствует формуле:
- Di = m(z-2,5m).
- Полная высота:
- h = h’+h“,
- и если выполнить подстановку, то получим:
- h = 1m+1,25m=2,25m.
- Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.
- Следующий важный размер, толщину зубца s принимают приблизительно равной:
- для отлитых зубцов: 1,53m:
- для выполненных путем фрезерования-1,57m, или 0,5×t
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
- для отлитых зубцов: sв=πm-1,53m=1,61m:
- для выполненных путем фрезерования- sв= πm-1,57m = 1,57m
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
- усилия, прикладываемые к детали при эксплуатации;
- конфигурация деталей, взаимодействующих с ней.
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.
Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
Результаты расчетов
- Для более крупных потребуются измерения и вычисления.
- Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
- m=De/(z+2)
- Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
Расчет параметров колеса и шестерни косозубой передачи
Расчетные формулы для важнейших характеристик шестерни косозубой передачи совпадают с формулами для прямозубой. Существенные различия возникают лишь при прочностных расчетах.
Источник: https://stankotec.ru/raznoe/modul-zuba-modul-shesterni-formuly-raschyota.html
Расчёт модулей зубчатых колёс
|
< Предыдущая СОДЕРЖАНИЕ Следующая >
Перейти к загрузке файла |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ориентировочное минимально допустимое значение модуля m, мм. определим по формуле: где km — вспомогательный коэффициент; М1 — крутящий момент на шестерне, Н•м; z1 — число зубьев шестерни; kFв — коэффициент учитывающий неравномерность распределения нагрузки по ширине венца; шbd — отношение ширины венца к начальному диаметру шестерни; yF1 — коэффициент учитывающий форму зуба. Допустимое напряжение зубьев по изгибу уFP определяют по формуле у’FP — допускаемое напряжение зубьев по изгибу, МПа, соответствующее базовому числу циклов перемены напряжений; kFL — коэффициент долговечности. Ориентировочное минимально допустимое значение модуля: Рассчитанный по формуле модуль округляется до стандартного значения m=2. Характеристики зубчатых колёс сведём в таблицу:
|
Расчёт на контактную выносливость рабочих поверхностей зубьев
Действующие в передаче контактные напряжения определяют по формуле
где ун — контактные напряжения, МПа; zН — коэффициент, зависящий от угла наклона зубьев, для x=0 применяем zН=1,76; zМ — коэффициент, учитывающий механические свойства материалов сопряжённых колёс, для стальных колёс zМ=275; zе — коэффициент, учитывающий суммарную длину контактных линий:
Коэффициент торцевого перекрытия:
где z1 и z2 — числа зубьев шестерни и колеса, знак «+» принимают для наружного зацепления.
Удельную расчётную окружную силу щHt определяют по формуле
где Pt — исходная окружная сила, Н:
где щHV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм.
Допускаемое контактное напряжение [ун] определяем по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kHL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kHL=1.
- Для стали 45 с улучшением =750 МПа.
- 532,25 МПа ? 750 МПа
- Условие контактной выносливости выполняется.
- Расчёт на изгибную выносливость зубьев
- Действующее в передаче напряжение изгиба сравнивается с допустимыми, с учётом коэффициента долговечности.
- Действующее напряжение изгиба:
Коэффициент yе — учитывает перекрытие зубьев. Для прямозубых колёс применяют yе=1. Коэффициент yв учитывает наклон зуба. Для прямозубых применяют yв=1.
Удельную расчётную окружную силу щFt определяем по формуле
где Pt — расчётная окружная сила в зубчатом зацеплении, Н; bщ — рабочая ширина венца, мм
Окружная сила Pt=2•103•M1/d1, где M1 — крутящий момент, Н•м; d1 — диаметр делительной окружности, мм.
Коэффициент kFa учитывает распределение нагрузки между зубьями. Для прямозубых передач приметаем kFa=1. Коэффициент kFв учитывает распределение нагрузки по ширине венца, можно принять kFв=1.1.
Коэффициент kFv учитывает динамическую нагрузку, возникающую в зацеплении.
где щFV — удельная окружная динамическая сила, Н/мм,
где V — окружная скорость, м/с; ащ — межосевое расстояние, мм; для прямозубых передач д=0.016; коэффициент g=47, учитывает влияние разности шагов зацепления.
Допускаемое изгибное напряжении [уF] определяется по формуле:
где — допускаемое контактное напряжение, соответствующее базовому числу циклов перемены напряжений, МПа; kFL — коэффициент долговечности, для зубчатых колёс коробки скоростей станков kFL=1.
Для стали Для стали 45 с улучшением у‘F=450 МПа, условие изгибной выносливости выполняется.
265.49 МПа ? 450 МПа
Условие на изгибную выносливость выполняется.
Источник: https://studbooks.net/2523612/tovarovedenie/raschyot_moduley_zubchatyh_kolyos



















