Как найти площади диагональных сечений усеченной пирамиды

найдите площадь диагонального сечения правильной усеченной четырехугольной пирамиды если ее высота равна корень из двух

Знаток

(309),
закрыт

7 лет назад

Усечённой пирамидой  ABCDA₁B₁C₁D₁  называется часть пирамиды  SABCD, заключённая между её основанием и секущей плоскостью, параллельной основанию.

Основаниями усечённой пирамиды называются параллельные грани  ABCD  и  A₁B₁C₁D₁  (ABCD – нижнее основание, A₁B₁C₁D₁ – верхнее основание).

Высотой усечённой пирамиды называется отрезок прямой, перпендикулярный её основаниям и заключённый между их плоскостями.

Усечённая пирамида называется правильной, если её основания – правильные многоугольники и прямая, соединяющая центры оснований, перпендикулярна плоскости оснований.

Апофемою правильной усечённой пирамиды называют высоту её боковой грани.

Свойства  усечённой пирамиды.

Основания – подобные многоугольники.

Боковые грани – трапеции.

Отношение высоты к высоте пирамиды, из которой она получена, равно отношению разности сторон одной грани к длине нижнего основания этой самой грани.

Поверхность усечённой пирамиды.

Площадь боковой поверхности усечённой пирамиды равна сумме площадей её боковых граней.

Полная поверхность усечённой пирамиды равна сумме площади боковой поверхности и площадей оснований.

В правильной четырёхугольной усечённой пирамиде стороны оснований равны  5  и  11 дм, а диагональ пирамиды – 12 дм. Определите боковую поверхность пирамиды.

АС = 11√͞͞͞͞͞2  (дм),  
A₁С₁ = 5√͞͞͞͞͞5  (дм).

S_бок = ¹/₂ (44 + 20)×5 = 160 (дм²).

ОТВЕТ:

S = 160 дм² = 1,6 м². 

ЗАДАЧА:

Высота правильной четырёхугольной усечённой пирамиды
равна  4
см. Стороны оснований равны  2
см  и 
8 см. Найдите площадь диагональных сечений.

РЕШЕНИЕ:

Начертим чертёж.

Диагональные сечения 
AA₁C₁D  и  BB₁D₁D– равные равнобедренные трапеции с высотой  ОО₁ = h = 4 см  и с основаниями
– диагоналями оснований  АС  и  А₁С₁  та  ВD  и  В₁D₁  соответственно. ABCD – квадрат, а поэтому

AC² = AD² + CD² =

= 8² + 8² = 128,

AC = √͞͞͞͞͞128 = 8√͞͞͞͞͞2 (cм).

A₁B₁C₁D₁ – квадрат, а поэтому

A₁C₁² = A₁D₁² + C₁D₁² = 2² + 2² = 8,

A₁C₁ = √͞͞͞͞͞8 = 2√͞͞͞͞͞2 (cм).

ОТВЕТ:  20√͞͞͞͞͞2 (cм²)

ЗАДАЧА:

В правильной четырёхугольной усечённой пирамиде высота
равна  2
см, а стороны оснований – 3 см  и  5
см. Найдите диагональ этой пирамиды.

РЕШЕНИЕ:

Начертим чертёж.

Диагональным сечением данной пирамиды
является равнобедренная трапеция  АА₁С₁С.

Так как 
А₁С₁  и  АС –
диагонали квадратов, А₁В₁С₁D₁  и  ABCD, то 

А₁С₁ = А₁В₁ ∙ √͞͞͞͞͞2 = 3√͞͞͞͞͞2 (см)  и  

АС = АВ ∙ √͞͞͞͞͞2 = 5√͞͞͞͞͞2 (см).

Проведём 
А₁К ⊥
АС 
и  С₁Н ⊥ АС. Тогда  А₁С₁НК – прямоугольник
и  А₁С₁ =
КН. Так что, прямоугольные треугольники  АА₁К  и  СС₁Н  равны по гипотенузе и катету.

Тогда,

АК = СН = ¹/₂ (АС – А₁С₁) =

^= 1/₂ (5√͞͞͞͞͞2 – 3√͞͞͞͞͞2) = √͞͞͞͞͞2  (см).

Тогда,

СК = АС – АК = 5√͞͞͞͞͞2 – √͞͞͞͞͞2 =
4√͞͞͞͞͞2  (см),

и по
теореме Пифагора в  ∆ А₁СК:

ОТВЕТ:  6 см

ЗАДАЧА:

В правильной четырёхугольной пирамиде плоскость, проведённая
параллельно основанию, делит высоту пирамиды пополам. Найдите сторону основания,
если площадь сечения равна  36 см².

РЕШЕНИЕ:

Пусть  SABCD – данная правильная пирамида,

основание – квадрат 
ABCD, SO – высота, O –
точка пресечения диагоналей квадрата, φ – плоскость сечения, О₁ –
точка пересечения  φ  и  SO, φ ∥ (ABC), S = 36 cм².

Поскольку  φ ∥ (ABC),
то прямые пересечения  𝜑  и боковых граней параллельны соответственно рёбрам
основания:

A₁B₁ ∥ AB, B₁C₁ ∥ BC, C₁D₁ ∥ CD,

A₁D₁ ∥ AD, 𝜑 ⊥ SO,

можно рассмотреть гомотетию с центром  S  и коэффициентом 

которая преобразует квадрат  ABCD  в квадрат 
А₁В₁С₁D₁, стороны которого в два раза меньше, а

S_ABCD = 4S_А1В1С1D1 = 4 ∙ 36 (см²).

S_ABCD = a² = 4 ∙
36,

a = 2 ∙ 6
= 12 (см).

ОТВЕТ:  12 см

• Урок 1. Прямые и плоскости в пространстве
• Урок 2. Прямая призма
• Урок 3. Наклонная призма
• Урок 4. Правильная призма
• Урок 5. Параллелепипед
• Урок 6. Прямругольный параллелепипед
• Урок 7. Куб
• Урок 8. Пирамида
• Урок 9. Правильная пирамида
• Урок 11. Цилиндр
• Урок 12. Вписанная и описанная призмы
• Урок 13. Конус
• Урок 14. Усечённый конус
• Урок 15. Вписанная и описанная пирамиды
• Урок 16. Сфера и шар
• Урок 17. Комбинация тел

Найдите площадь диагонального сечения правильной усеченной пирамиды, если ее высота равна корень2, а второны равны 1 и 4.

ПОЖАЛУЙСТА!

Определение 1

Усечённая пирамида
— часть пирамиды, заключенная между её основанием, боковыми гранями и сечением этой пирамиды плоскостью, параллельной основанию.

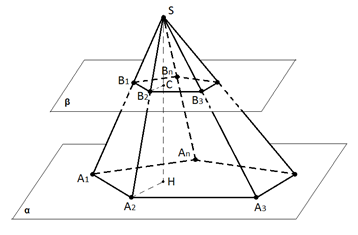
Рис. 1. Усечённая пирамида A₁A₂A₃…A_nB₁B₂B₃…B_n

Многоугольники A1A2A3…An и B1B2B3…Bn называются основаниями усечённой пирамиды.

Многоугольники A1A2B2B1, A2A3B3B2, …, AnA1B1Bn называются боковыми гранями усечённой пирамиды.

Отрезки A1B1, A2B2, …, AnBn называются боковыми рёбрами усечённой пирамиды.

На рисунке также показана высота SH исходной пирамиды и высота CH усечённой пирамиды.

Определение 2

Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется
высотой усечённой пирамиды
.

Определение 3

Правильной усеченной пирамидой
 называется усеченная пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию.

Теорема 1

Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.

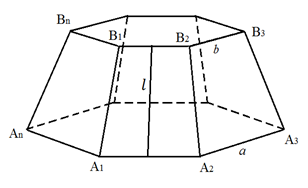
Рис. 2. К доказательству теоремы 1

Боковые грани правильной усечённой пирамиды – равные между собой равнобедренные трапеции с одним и тем же верхним основанием a, нижним b и высотой (апофемой) l (рис. 2). Поэтому площадь одной грани равна 12·(a+b)·l. Площадь всех граней, т.е. боковая поверхность, равна 12·(an+bn)·l, где 
n – число вершин у основания пирамиды, an и bn – периметры оснований пирамиды.

Теорема доказана. 

Пример 1

Высота правильной четырёхугольной усечённой пирамиды равна 7 см. Стороны оснований равны 10 см и 2 см. Найдите боковое ребро пирамиды.

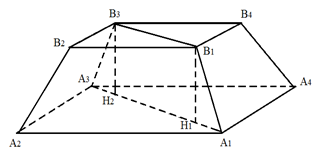
Рис. 3. К примеру 1

Пусть квадраты A1A2A3A4 и B1B2B3B4 являются основаниями правильной четырёхугольной усечённой пирамиды (рис. 3).

По условию A1A2=10 см, B1B2=2 см.

Диагональное сечение этой призмы A1A3B3B1 является равнобедренной трапецией с основаниями A1A3 и B1B3.

Найдём эти основания.

A1A3=A2A32+A1A22=102+102=200=102,

B1B3=B2B32+B1B22=22+22=8=22.

По условию высота пирамиды равна 7 см.  Значит, в прямоугольном треугольнике A1B1H1 катет B1H1 равен 7 см. Найдём катет A1H1.

A1H1=A1A3-B1B32=102-222=42.

Найдём теперь боковое ребро усечённой пирамиды A1B1, которое является гипотенузой прямоугольного треугольника A1B1H1.

A1B1=A1H12+B1H12=422+72=32+49=81=9 см.

Ответ: 9 см.

Пример 2

Стороны оснований правильной усечённой треугольной пирамиды 4 дм и 1 дм. Боковое ребро 2 дм. Найдите высоту пирамиды.

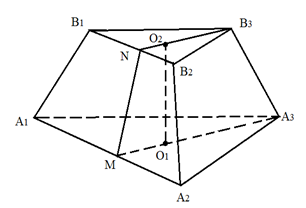
Рис. 4. К примеру 2

Центры оснований O1 и O2 правильной треугольной пирамиды A1A2A3B1B2B3 (рис. 4) делят медианы оснований A3M и B3N в отношении 2:1 считая от вершин A3 и B3. Отрезок O1O2 является высотой пирамиды. 

Найдём сначала медианы равносторонних треугольников A1A2A3 и B1B2B3 (они также являются и высотами этих треугольников).

Упражнение 1

1. В правильной усеченной четырёхугольной пирамиде высота равна 2 см, а стороны оснований 3 см и 5 см. Найдите диагональ этой пирамиды.

2. Стороны оснований усечённой правильной треугольной пирамиды 2 см и 6 см. Боковая грань образует с большим основанием угол 60^o. Найдите высоту.

3. Высота правильной четырёхугольной усечённой пирамиды равна 4 см. Стороны оснований равны 2 см и 8 см. Найдите площади диагональных сечений.

4. В правильной четырёхугольной усечённой пирамиде стороны оснований 8 м и 2 м. Высота пирамиды равна 4 м. Найдите площадь полной поверхности.

Контрольные вопросы

1. Сформулируйте определение усечённой пирамиды.
2. Какая усечённая пирамида называется правильной?
3. Сформулируйте и докажите теорему о площади боковой поверхности правильной усечённой пирамиды.

Ответы