В данной публикации мы рассмотрим, как можно вычислить площадь поверхности правильной призмы разных видов (треугольной, четырехугольной и шестиугольной), а также, разберем примеры решения задач для закрепления материала.
Правильная призма – это прямая призма, основанием которой является правильный многоугольник. А прямой фигура является в том случае, если ее боковые грани перпендикулярны основаниям.
-
Формула площади правильной призмы
- 1. Общая формула
-
2. Площадь правильной треугольной призмы
- 3. Площадь правильной четырехугольной призмы
- 4. Площадь правильной шестиугольной призмы
- Примеры задач
Формула площади правильной призмы
1. Общая формула
Площадь (S) полной поверхности призмы равна сумме площади ее боковой поверхности и двух площадей основания.
Sполн. = Sбок. + 2Sосн.
Площадь боковой поверхности прямой призмы равняется произведению периметра ее основания на высоту.
Sбок. = Pосн. ⋅ h
Формула периметра и площади основания правильной призмы зависит от вида многогранника. Ниже мы рассмотрим самые популярные виды.
2. Площадь правильной треугольной призмы
Основание: равносторонний треугольник.
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 3ah |
| полная |  |
microexcel.ru
3. Площадь правильной четырехугольной призмы
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 4ah |
| полная | Sполн. = 2a2 + 4ah |
microexcel.ru
Примечание: Если высота правильной четырехугольной призмы равняется длине стороны ее основания, значит мы имеем дело с кубом, площадь одной грани которого равна a2. А так как все шесть граней куба равны, то полная площадь его поверхности равняется 6a2.
4. Площадь правильной шестиугольной призмы
Основание: правильный шестиугольник
| Площадь | Формула |
| основание |  |
| боковая поверхность | Sбок. = 6ah |
| полная |  |
microexcel.ru
Примеры задач
Задание 1:
Сторона правильной треугольной призмы равна 6 см, а ее высота – 8 см. Найдите полную площадь поверхности фигуры.
Решение:
Воспользуемся подходящей формулой, подставив в нее известные нам значения:
Задание 2:
Площадь полной поверхности правильной шестиугольной призмы составляет 400 см2. Найдите ее высоту, если известно, что сторона основания равна 5 см.
Решение:
Выведем выражение для нахождения высоты призмы из формулы ее полной площади:
Загрузить PDF
Загрузить PDF
Призма представляет собой объемную (трехмерную) фигуру с двумя параллельными (и равными) гранями.[1]
Две параллельные грани являются треугольниками и называются основаниями. Также в треугольной призме есть три боковые грани. Чтобы найти площадь поверхности треугольной призмы, сначала нужно вычислить площадь боковой поверхности, затем вычислить общую площадь оснований и, наконец, сложить эти площади. Площадь поверхности призмы находится по формуле: 



-
1
-
2
Вычислите периметр одного основания. Основание представляет собой треугольник, поэтому имеет три стороны. Периметра треугольника вычисляется по формуле:
, где
,
,
– стороны треугольника.[4]
Не имеет значения, какое основание рассматривать, так как оба основания равны.[5]
- Например, стороны основания равны 6 см, 5 см и 4 см; чтобы вычислить периметр, нужно сложить три стороны:
. Таким образом, периметр одного основания равен 15 см.
- Например, стороны основания равны 6 см, 5 см и 4 см; чтобы вычислить периметр, нужно сложить три стороны:
-
3
Подставьте периметр основания в формулу для вычисления площади боковой поверхности призмы. Значение периметра подставляется вместо
.
- Например,
.
- Например,
-
4
Подставьте высоту призмы в формулу для вычисления площади боковой поверхности призмы. Высота призмы равна любой стороне боковой грани, которая не принадлежит основанию. Как правило (но не всегда), такой стороной является более длинная сторона боковой грани.
- Например, если высота призмы равна 9 см, формула запишется так:
.
- Например, если высота призмы равна 9 см, формула запишется так:
-
5
Перемножьте периметр одного основания и высоту призмы. Получится площадь боковой поверхности призмы (в квадратных единицах). Это первое значение, необходимое для вычисления площади поверхности призмы (вторым значением является площадь основания).
- Например,
. Таким образом, площадь боковой поверхности призмы равна 135 см2.
Реклама
- Например,
-
1
-
2
Подставьте основание треугольника в формулу для вычисления площади треугольника. Не перепутайте основание с другой стороной треугольника. Основание – это сторона, к которой проведена высота (то есть сторона, перпендикулярная высоте).
- Например, если основание треугольника равно 6 см, формула запишется так:
.
- Например, если основание треугольника равно 6 см, формула запишется так:
-
3
Подставьте высоту треугольника в формулу для вычисления площади треугольника. Умножьте основание на высоту, а результат разделите на 2. Получится площадь основания (в квадратных единицах). Это второе значение, необходимое для вычисления площади поверхности призмы.
Реклама
-
1
Запишите формулу для вычисления площади поверхности призмы. Формула:
, где где
– площадь поверхности,
– площадь боковой поверхности,
– площадь одного основания.[8]
-
2
Подставьте площадь боковой поверхности в формулу. Это общая площадь трех боковых граней (то есть площади оснований не учитываются), которая была вычислена в первом разделе. Площадь боковой поверхности подставляется вместо
.
- В нашем примере площадь боковой поверхности равна 135 см2, поэтому формула запишется так:
.
- В нашем примере площадь боковой поверхности равна 135 см2, поэтому формула запишется так:
-
3
Подставьте площадь основания в формулу. Подставляйте площадь только одного основания, а не сумму площадей двух оснований. Площадь основания подставляется вместо
.
- В нашем примере площадь основания равна 9,9 см2, поэтому формула запишется так:
.
- В нашем примере площадь основания равна 9,9 см2, поэтому формула запишется так:
-
4
Проведите вычисления. Умножьте площадь основания на 2, а затем к результату прибавьте площадь боковой поверхности. Получится площадь поверхности треугольной призмы (в квадратных единицах).
Реклама
Об этой статье
Эту страницу просматривали 163 917 раз.
Была ли эта статья полезной?
На чтение 4 мин Просмотров 65.6к. Опубликовано 13 февраля, 2019
Здесь вы найдёте: Объем правильной треугольной призмы понятие, Объем призмы треугольной формула нахождения, Площадь треугольной призмы
Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.
Содержание
- Призма треугольная — определение
- Элементы треугольной призмы
- Виды треугольных призм
- Прямая треугольная призма
- Наклонная треугольная призма
- Основные формулы для расчета треугольной призмы
- Объем треугольной призмы
- Площадь боковой поверхности призмы
- Площадь полной поверхности призмы
- Правильная призма — прямая призма, основанием которой является правильный многоугольник.
- Пример призмы
- Задачи на расчет треугольной призмы
Призма треугольная — определение
Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.
Элементы треугольной призмы
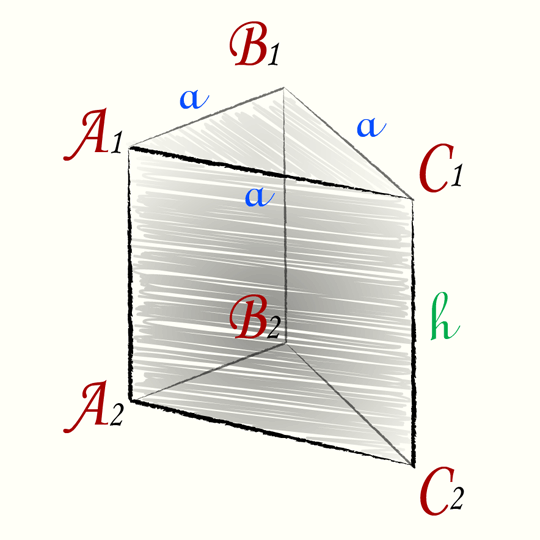
Треугольники ABC и A1B1C1 являются основаниями призмы.
Четырехугольники A1B1BA, B1BCC1 и A1C1CA являются боковыми гранями призмы.
Стороны граней являются ребрами призмы (A1B1, A1C1, C1B1, AA1, CC1, BB1, AB, BC, AC), всего у треугольной призмы 9 граней.
Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).
Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.
Площадь основания — это площадь треугольной грани призмы.
Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.
Виды треугольных призм
Треугольная призма бывает двух видов: прямая и наклонная.
У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)
Прямая треугольная призма
Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.
Наклонная треугольная призма
Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.
Основные формулы для расчета треугольной призмы
Объем треугольной призмы
Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.
Объем призмы = площадь основания х высота
или
V=Sосн . h
Площадь боковой поверхности призмы
Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.
Площадь боковой поверхности треугольной призмы = периметр основания х высота
или
Sбок=Pосн.h
Площадь полной поверхности призмы
Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.
так как Sбок=Pосн.h, то получим:
Sполн.пов.=Pосн.h+2Sосн
Правильная призма — прямая призма, основанием которой является правильный многоугольник.
Свойства призмы:
Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.
Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см2, то высота должна быть выражена в сантиметрах, а объем — в см3 . Если площадь основания в мм2, то высота должна быть выражена в мм, а объем в мм3 и т. д.
Пример призмы
В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.
Задачи на расчет треугольной призмы
Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:
V = 1/2 · 6 · 8 · 5 = 120.
Задача 2.
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.
Решение:
Объём призмы равен произведению площади основания на высоту: V = Sосн ·h.
Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S2 = S1k2 = S122 = 4S1.
Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.
Таким образом, искомый объём равен 20.
A polyhedron with two triangular bases and three rectangular sides is known as a triangular prism. It’s a three-dimensional object with three side faces and two base faces, all of which are connected by edges. Its sides are rectangular in form and are joined together side by side. Triangle cross-sections go parallel to the base faces. The two triangular bases are congruent and parallel to one another. There are nine unique nets in this pentahedron. The bases’ edges and vertices are linked to one another. It’s termed a right triangle prism if the sides are rectangular; otherwise, it’s called an oblique triangular prism.
Surface area of Triangular Prism formula
The surface area of a triangular prism is defined as the sum of the area of its five faces. To calculate the surface area, we need the values of the base, length, and height of the triangular prism. Its formula equals the sum of two times the base area and three times the product of the base and length of the prism. Its unit of measurement is a meter square (sq. m).
A = bh + 3bl
Where,
b is the triangular base,
h is the height,
l is the length of the prism.
How to find the surface area of a Triangular Prism?
Let’s take an example to understand how we can calculate the surface area of a triangular prism.
Example: Calculate the surface area of a triangular prism of base 5 m, height 10 m and length 15 m.
Step 1: Note the dimensions of the triangular prism. In this example, the length of the base is 5 m, height is 10 m and length is 15 m.
Step 2: We know that the surface area of a triangular prism is equal to (bh + 3bl). Substitute the given values of base, height and length in the formula.
Step 3: So, the surface area of triangular prism is calculated as, A = 5 (10) + 3 (5) (15) = 275 sq. m
Sample Problems
Problem 1: Calculate the surface area of a triangular prism of base 6 m, height 3 m, and length 7 m.
Solution:
We have,
b = 6
h = 3
l = 7
Using the formula we get,
A = bh + 3bl
= 6 (3) + 3 (6) (7)
= 144 sq. m
Problem 2: Calculate the surface area of a triangular prism of base 2 m, height 4 m, and length 6 m.
Solution:
We have,
b = 2
h = 4
l = 6
Using the formula we get,
A = bh + 3bl
= 2 (4) + 3 (2) (6)
= 44 sq. m
Problem 3: Calculate the surface area of a triangular prism of base 4 m, the height of 9 m, and length of 7 m.
Solution:
We have,
b = 4
h = 9
l = 7
Using the formula we get,
A = bh + 3bl
= 4 (9) + 3 (4) (7)
= 120 sq. m
Problem 4: Calculate the length of the triangular prism if its base is 4 m, height is 9 m and area is 198 sq. m.
Solution:
We have,
b = 6
h = 9
A = 198
Using the formula we get,
A = bh + 3bl
=> 198 = 6 (9) + 3 (6) (l)
=> 198 = 54 + 18l
=> 18l = 144
=> l = 8 m
Problem 5: Calculate the length of the triangular prism if its base is 5 m, height is 10 m and area is 180 sq. m.
Solution:
We have,
b = 5
h = 10
A = 180
Using the formula we get,
A = bh + 3bl
=> 180 = 5 (10) + 3 (5) (l)
=> 180 = 54 + 15l
=> 15l = 126
=> l = 8.4 m
Problem 6: Calculate the height of the triangular prism if its base is 12 m, length is 14 m and area is 700 sq. m.
Solution:
We have,
b = 12
l = 14
A = 700
Using the formula we get,
A = bh + 3bl
=> 700 = 12 (h) + 3 (12) (14)
=> 700 = 12h + 504
=> 12h = 196
=> h = 16.33 m
Problem 7: Calculate the height of the triangular prism if its base is 8 m, length is 14 m and area is 408 sq. m.
Solution:
We have,
b = 8
l = 14
A = 408
Using the formula we get,
A = bh + 3bl
=> 408 = 8 (h) + 3 (8) (14)
=> 408 = 8h + 336
=> 8h = 72
=> h = 9 m
Last Updated :
01 Jun, 2022
Like Article
Save Article
Площадь правильной треугольной призмы
Нарисуем правильную треугольную призму:
Площадь правильной треугольной призмы
Как мы видим — призма имеет два основания, эти основания правильные треугольники со стороной a, и три боковых стороны, которые представляют из себя прямоугольники со сторонами a и h
Таким образом площадь правильной треугольной призмы складывается из двух площадей оснований и трех площадей боковых граней.
[ S_{призмы} = 2S_{осн} + 3S_{бок} ]
Подставим сюда формулу площади прямоугольника и формулу площади равностороннего треугольника и получим:
[ S_{призмы} = 2frac{sqrt{3}}{4}a^2 + 3ah ]
или
[ S_{призмы} = a(frac{sqrt{3}}{2}a + 3h) ]
Вычислить, найти площадь правильной треугольной призмы по формуле (3)
Площадь правильной треугольной призмы |
стр. 331 |
|---|