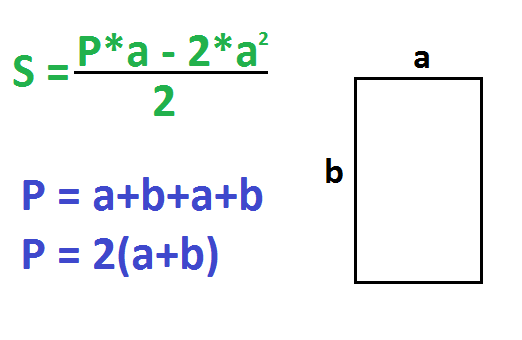Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
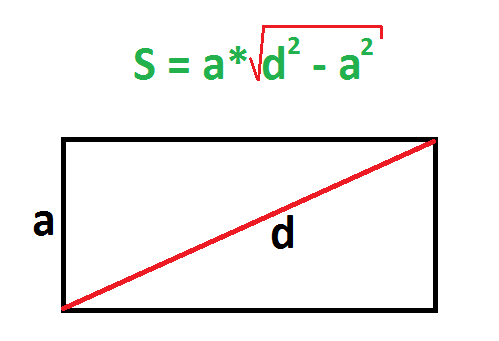
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
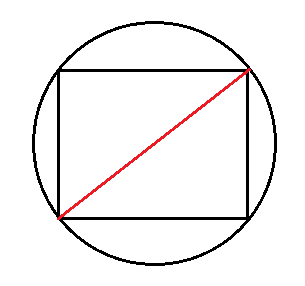
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
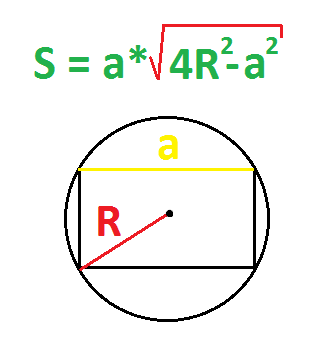
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
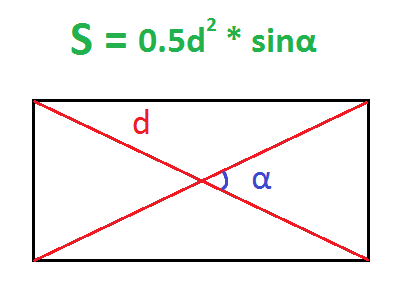
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
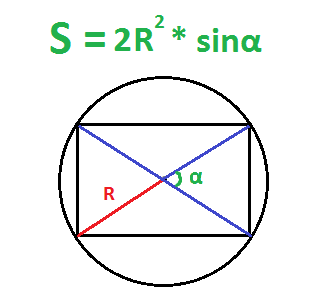
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Площадь прямоугольника. Онлайн-калькулятор
Онлайн-калькулятор площади прямоугольника поможет вам точно и быстро рассчитать или проверить расчеты по нахождению площади любого прямоугольника. Обычно площадь прямоугольника можно рассчитать двумя способами: через две стороны прямоугольника или через его диагонали. При первом способе расчета введите значения длин сторон a и b. При втором – длину диагоналей и значение угла между ними в градусах или радианах. Помимо ответа калькулятор покажет решение.
Способ расчета площади прямоугольника:
Стороны прямоугольника:
a =
b =
Рассчитать
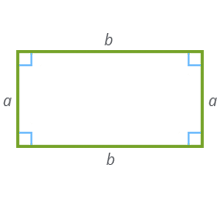
Прямоугольник – это геометрическая фигура, представляющая собой четырехугольник, у которого все углы прямые (90° ). Диагонали прямоугольника равны между собой.
Как найти площадь прямоугольника?
Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:
1) через две стороны
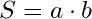
a, b – стороны
2) через диагонали и угол
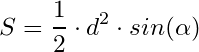
d – диагонали,
α – угол между диагоналями.
Как рассчитать площадь прямоугольника
На данной странице калькулятор поможет рассчитать площадь прямоугольника онлайн. Для расчета задайте длину сторон или длины диагоналей и угол между ними.
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Через стороны
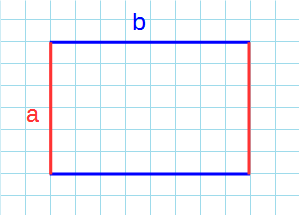
Формула для нахождения площади прямоугольника через стороны:
a, b – стороны прямоугольника.
Через диагонали и угол между ними
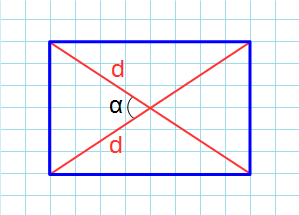
Формула для нахождения площади прямоугольника через диагонали и угол между ними:
d – диагональ; α – угол между диагоналями.
Как найти площадь прямоугольника?
Анонимный вопрос
18 августа 2019 · 203,7 K
Редактор, автор и переводчик книг по математике · 18 авг 2019 ·
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину
Обрати внимание, что длина и ширина должны быть выражены в одних единицах. Если длина и ширина в сантиметрах, то площадь получится в сантиметрах квадратных; если длина и ширина в километрах, то площадь получится в квадратных километрах. Если длина и ширина выражены в разных единицах, сначала приведи к одинаковым, а потом уж умножай.
Очень полезно познакомиться с площадями прямоугольников на практике. Давай я попробую угадать: площадь твоего стола меньше одного квадратного метра. Площадь твоей кровати больше одного квадратного метра, но меньше двух. Площадь твоей комнаты больше 10 квадратных метров и меньше 20 квадратных метров. Мне не видно, и я могла ошибиться. Так что измерь, посчитай и проверь, правильно ли я угадала.
120,7 K
площадь- это длина умноженая на ширину
Комментировать ответ…Комментировать…
7,1 K
Комментировать ответ…Комментировать…
Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:
1) через две стороны
S=a*b
2) через диагонали и угол
S=1/2*d(в квадрате)*sin(α)… Читать далее
7,6 K
Комментировать ответ…Комментировать…
Надо длину умножить на ширину
Пример : 3*2 = 6 квадратных сантиметров ( квадратные сантиметры пишутся так : см и мелкая 2 на верху) так же есть и другие квадратные
5,6 K
Комментировать ответ…Комментировать…
Пример:
У прямоугольника есть 4 стороны. Первые 2 стороны равны друг другу, как и вторые 2 стороны.
Значит, прямоугольник делится на a и b. Представим, что сторона a – 3 сантиметра, а b – 2 сантиметра. Площадь будет буквой S. Чтобы вычислить площадь прямоугольника, нужно сторону a умножить на b. S=a*b. S=3*2. 3*2 это шесть. Площадь обозначается квадратными сантиметрами. S=6 см2
5,1 K
-Как найти площадь Ленина?
-Надо длину Ленина, умножить на ширину Ленина!
Комментировать ответ…Комментировать…
Геймер, програмер, учу английский, чуть-чуть ютубер · 4 мая 2021
У прямоугольника есть длина и ширина.
Длину и ширину надо перемножить.
Ответ надо записывать в квадратной величине (результат и маленькая двойка сверху)
Пример:
Ширина = 3 см
Длина = 7 см
7*3 = 21(см2)
Ответ: 21 см2. Читать далее
2,5 K
Возьмите 2 игральных кубика. Бросьте оба. Первый показывает вам ширину прямоугольника, второй – длину. А площадь -… Читать дальше
Комментировать ответ…Комментировать…
Чтобы найти площадь прямоугольника, нужно умножить две его неравные стороны друг на друга. Также это выражается формулой S = a * b, где S – площадь, a и b – две неравные стороны прямоугольника.
В общей сложности, площадь прямоугольника, можно найти с помощью пяти разных формул.
1. Через две смежные стороны
2. Через любую сторону и периметр
3. Через любую сторону и… Читать далее
9,4 K
Комментировать ответ…Комментировать…
Что бы найти площадь треугольника, нужно воспольщоваться формулой:
S= a•b
Например:
Длина прямоугольника равна 8 см
Ширина прямоугольника равна 4см
Площадь прямоугольника равна 8•4=32 Читать далее
1,5 K
Комментировать ответ…Комментировать…
Чтобы найти площадь прямоугольника надо умножить длину на ширину пример:
a-9 см
b-3 см
s-? см
s=a*b
9*3=27(см)
Ответ:27 сантиметров площадь прямоугольника. Читать далее
2,5 K
Комментировать ответ…Комментировать…
Я работаю сама на себя – плету из бисера украшения и продаю. · 25 окт 2022
Для того чтобы найти площадь прямоугольника надо одну сторону прямоугольника (ширину) умножить на вторую сторону (длина).
Ширина – а
Длина – б
площадь – S
S = а умножить на б
356
Комментировать ответ…Комментировать…
Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.
11 367
Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.
По диагонали и стороне
Должна быть известна диагональ и любая из сторон. Действия:
- Найти квадрат диагонали, то есть умножить ее на саму себя.
- Найти квадрат известной стороны.
- Из квадрата диагонали вычесть квадрат стороны.
- Найти квадратный корень получившейся разности.
- Умножить его на известную сторону.
Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.
- Квадрат стороны = 3*3 = 9 см.
- Квадрат диагонали = 5*5 = 25 см.
- Вычитаю из квадрата диагонали квадрат стороны: 25-9 = 16 см.
- Нахожу квадратный корень получившейся разности. Корень из 16 = 4 см.
- Умножаю корень разности на известную сторону: 16*9 = 144 см.
Ответ: 144 см.
Обратите внимание
Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.
По стороне и диаметру описанной окружности
Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.
Действия:
- Найдите квадрат диаметра – умножьте диаметр на диаметр.
- Найдите квадрат известной стороны.
- Отнимите от квадрата диаметра квадрат стороны.
- Найдите квадратный корень разности.
- Умножьте квадратный корень на известную сторону.
Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.
- Квадрат диаметра: 10*10 = 100 см.
- Квадрат стороны: 8*8 = 64 см.
- Отнимаю от квадрата диаметра квадрат стороны: 100-64 = 36 см.
- Квадратный корень из 36 равен 6 см (потому что 6*6 = 36).
- Умножаю сторону на корень из разности: 8*6 = 48 см.
Ответ: 48 см.
Лайфхак
Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:
А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.
Диаметр равен двум радиусам, потому что радиус – это половина диаметра.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
По радиусу описанной окружности и стороне
Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.
Другой способ:
- Найти квадрат радиуса (умножьте радиус на радиус).
- Умножить квадрат радиуса на 4.
- Найти квадрат известной стороны.
- Отнять от четырех радиусов в квадрате квадрат известной стороны (из второго отнять третье).
- Найти квадратный корень разности.
- Умножить корень на известную сторону.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.
- Квадрат радиуса: 5*5=25 см.
- Четыре квадрата радиуса: 4*25 = 100 см.
- Квадрат стороны: 6*6 = 36 см.
- Отнимаю от четырех радиусов в квадрате квадрат стороны: 100-36 = 64 см.
- Нахожу квадратный корень разности. Корень из 64 равен 8 см.
- Умножаю корень на сторону: 8*6 = 48 см.
Ответ: 48 см.
Помните
Радиус = половине диаметра.
Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.
По стороне и периметру – 1 способ
Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).
Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.
Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.
- Нахожу вторую сторону прямоугольника:
- P=2(a+b).
- P=2a+2b.
- 14= 2*3+2b.
- 14 = 6+2b.
- 2b = 14-6 = 8.
- b = 8/2.
- b = 4.
- Нахожу площадь по основной формуле. S = 3*4 = 12 см.
Ответ: 12 см.
По стороне и периметру – 2 способ
Действия такие:
- Умножьте периметр на сторону.
- Найдите квадрат стороны.
- Умножьте квадрат стороны на 2.
- Отнимите от произведения периметра и стороны два квадрата стороны (от первого отнимите третье).
- Поделите на 2.
Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.
- Умножаю периметр на сторону: 8*28 = 224 см.
- Нахожу квадрат стороны: 8*8 = 64 см.
- Умножаю квадрат стороны на два: 64*2 = 84 см.
- Отнимаю из первого третье: 224-84 = 140 см.
- Делю разность на два: 140/2 = 70 см.
Ответ: 70 см.
По диагонали и углу между диагоналями
Диагонали прямоугольника всегда равны.
Действия:
- Найти квадрат диагонали (умножить диагональ на саму себя).
- Найти половину этого квадрата – умножить его на 0,5.
- Найти синус угла между диагоналями.
- Умножить половину квадрата диагонали на синус угла между диагоналями.
Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.
- Квадрат диагонали: 10*10 = 100 см.
- Половина этого квадрата: 0,5*100 = 50 см.
- Синус угла между диагоналями: sin 30 градусов = 0,5.
- Перемножаю половину квадрата и синус угла, чтобы найти площадь: 50*0,5 = 25 см.
Ответ: 25 см.
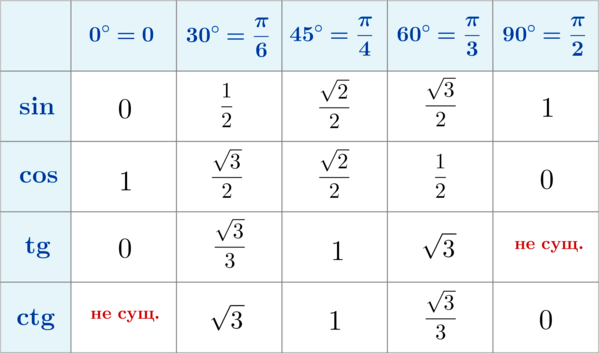
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).
По радиусу описанной окружности и углу между диагоналями – первый способ
Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.
- Находим длину диагонали: 6*2 =12 см.
- Квадрат диагонали равен 144 см.
- Половина квадрата: 72 см.
- Синус 30 градусов равен 0,5.
- Умножаем половину квадрата на синус: 72*0,5 = 36 см.
Ответ: 36 см.
По радиусу описанной окружности и углу между диагоналями – второй способ
Действия:
- Найти квадрат радиуса (умножить радиус на радиус).
- Умножить квадрат радиуса на два.
- Найти синус угла между диагоналями.
- Умножить синус угла на два радиуса в квадрате.
Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.
- Квадрат радиуса: 6*6 = 36.
- Два радиуса в квадрате: 36*2 = 72.
- Синус 30 градусов равен 0,5.
- Произведение синуса и двух радиусов в квадрате: 72*0,5 = 36 см.
Ответ: 36 см.
Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.
( 1 оценка, среднее 5 из 5 )
Оцените статью
ЕЖЕНЕДЕЛЬНАЯ РАССЫЛКА
Получайте самые интересные статьи по почте и подписывайтесь на наши социальные сети
ПОДПИСАТЬСЯ