В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.
- Определение сектора круга
-
Формулы нахождения площади сектора круга
- Через длину дуги и радиус круга
-
Через угол сектора (в градусах) и радиус круга
- Через угол сектора (в радианах) и радиус круга
- Примеры задач
Определение сектора круга
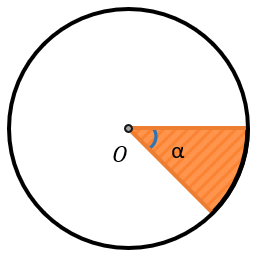
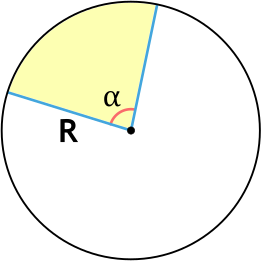
Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.

- AB – дуга сектора;
- R (или r) – радиус круга;
- α – это угол сектора, т.е. угол между двумя радиусами. Также его иногда называют центральным углом.
Формулы нахождения площади сектора круга
Через длину дуги и радиус круга
Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).
![]()
Через угол сектора (в градусах) и радиус круга
Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах (α°) и деленной на 360°.

Через угол сектора (в радианах) и радиус круга
Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (aрад) и квадрата радиуса круга.

Примеры задач
Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.
Решение
Воспользуемся первой формулой, подставив в нее заданные значения:
![]()
Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см2, а радиус круга – 8 см.
Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:
![]()
Круговой сектор — часть круга, которая ограничена дугой этого самого круга и двумя радиусами.
Онлайн-калькулятор площади сектора круга
Возьмем две произвольные точки, лежащие на границе круге. Они делят ее на две разные части, которые могут быть как одинаковыми по длине, так и разными. Эти части называются дугами круга.
Дуги равны по длине, когда равны углы, с помощью которых они образованы.
Рассмотрим задачу о нахождении площади сектора круга.
Формула площади сектора круга по радиусу и длине дуги
S=12⋅r⋅lS=frac{1}{2}cdot rcdot l
rr — радиус круга;
ll — длина дуги.
Рассмотрим решение задачи.
Найдите площадь кругового сектора, если известно, что длина дуги равна 20 (см.), а радиус круга равен 5 (см.).
Решение
r=5r=5
l=20l=20
В данной задаче сразу можно подставить наши числа в исходную формулу и вычислить площадь:
S=12⋅r⋅l=12⋅5⋅20=50S=frac{1}{2}cdot rcdot l=frac{1}{2}cdot 5cdot 20=50 (см. кв.)
Ответ: 50 см. кв.
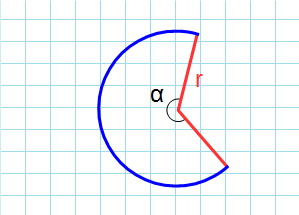
Формула площади сектора круга по радиусу и угла в радианах
S=12⋅r2⋅αS=frac{1}{2}cdot r^2cdot alpha
rr — радиус круга;
αalpha — центральный угол, измеряемый в радианах.
Пример решения задачи.
Найдите площадь кругового сектора, если радиус круга равен 8 (см.), а центральный угол кругового сектора равен π2frac{pi}{2} радиан.
Решение
r=8r=8
α=π2alpha=frac{pi}{2} рад.
По формуле получаем:
S=12⋅r2⋅α=12⋅82⋅π2≈50.2S=frac{1}{2}cdot r^2cdot alpha=frac{1}{2}cdot 8^2cdotfrac{pi}{2}approx50.2 (см. кв.)
Ответ: 50.2 см.кв.
Формула площади сектора круга по радиусу и углу в градусах
S=π360⋅r2⋅αS=frac{pi}{360}cdot r^2cdot alpha
rr — радиус круга;
αalpha — центральный угол, измеряемый в градусах.
Эту формулу можно получить используя связь между радианами и градусами:
2π рад.=360∘2pitext{ рад.}=360^{circ}
Найти площадь кругового сектора, если дан радиус круга равный 10 (см.), а центральный угол сектора равен 180180 градусов.
Решение
r=10r=10
α=180∘alpha=180^{circ}
Площадь данного сектора:
S=π360⋅r2⋅α=π360⋅102⋅180∘≈157S=frac{pi}{360}cdot r^2cdot alpha=frac{pi}{360}cdot 10^2cdot 180^{circ}approx157 (см. кв.)
Ответ: 157 см. кв.
Решение задач по геометрии онлайн от экспертов сайта Студворк!
Тест по теме “Площадь сектора круга”
Здесь вы можете рассчитать площадь сектора круга с помощью удобного онлайн калькулятора по двум формулам. Для этого необходимо ввести известные вам параметры фигуры:
- радиус круга и угол,
- длину дуги и радиус.
Сектор круга или окружности – это его(её) часть, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга (окружности).
Содержание:
- калькулятор площади сектора круга
- формула площади сектора круга через радиус и угол
- формула площади сектора круга через радиус и длину дуги
- примеры задач
Формула площади сектора круга через радиус и угол
S = pi R^2 dfrac{alpha °}{360°}
S = dfrac{alpha}{2} R^2
R – радиус сектора
α° – угол сектора (в градусах)
α – угол сектора (в радианах)
Формула площади сектора круга через радиус и длину дуги

S = dfrac{1}{2}LR
L – длина дуги сектора
R – радиус сектора
Примеры задач на нахождение площади сектора круга
Задача 1
Найдите площадь сектора круга радиуса 1 длина дуги которого равна 2.
Решение
Для решения задачи нам подойдет вторая формула.
S = dfrac{1}{2}LR = dfrac{1}{2} cdot 2 cdot 1 = dfrac{1}{2} cdot 2 = 1 : см^2
Ответ: 1 : см^2
Давайте проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь сектора круга радиуса 24 длина дуги которого равна 3.
Решение
Задача аналогична предыдущей.
S = dfrac{1}{2}LR = dfrac{1}{2} cdot 3 cdot 24 = dfrac{1}{2} cdot 72 = 36 : см^2
Ответ: 36 : см^2
Проверка .
Задача 3
Найдите площадь кругового сектора если радиус круга равен 3, а угол сектора равен 120°.
Решение
Для решения этой задачи нам потребуется первая формула, в которой угол указывается в градусах.
S = pi R^2 dfrac{alpha °}{360°} = pi cdot 3^2 cdot dfrac{120°}{360°} = pi cdot 9 cdot dfrac{1}{3} = 3 pi : см^2 approx 9.42478 : см^2
Ответ: 3 pi : см^2 approx 9.42478 : см^2
Проверка .
Как рассчитать площадь сектора круга
На данной странице калькулятор поможет рассчитать площадь сектора круга онлайн. Для расчета задайте радиус, длину дуги или угол сектора круга.
Сектор круга – это часть круга, окружности ограниченная дугой и двумя радиусами, проведенными к концам дуги.
Через длину дуги и радиус
Формула для нахождения площади сектора круга:
l – длина дуги окружности; r – радиус окружности.
Через угол и радиус
Формула для нахождения площади сектора круга:
— в градусах;
— в радианах;
π – константа равная (3.14); α – угол сектора круга; r – радиус окружности.
Площадь круга и сектора круга
-
ПЛОЩАДЬ КРУГА
Площадь круга равна произведению квадрата радиуса окружности и числа π.
(S = pi R^{2})
-
ПЛОЩАДЬ СЕКТОРА
Сектор – это часть круга, которая ограничена дугой и двумя радиусами.
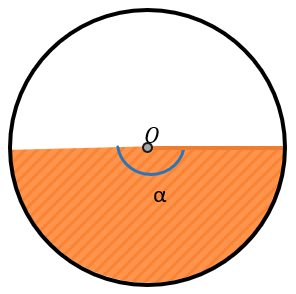
Чтобы понять, какую площадь занимает сектор, нужно понять, какую часть круга этот сектор занимает. Если сектор занимает половину круга, он выглядит так:
Понятно, что у такого полукруга (alpha = 180⁰,) т.к. два радиуса, ограничивающих сектор образуют диаметр. Получается, что
(frac{alpha}{360{^circ}} = frac{180{^circ}}{360{^circ}} = frac{1}{2})
Значит угол сектора напрямую связан с площадью, которую он занимает. В данном случае сектор занимает половину от круга, значит и его угол будет равен половине всего оборота круга – половине от 360⁰.
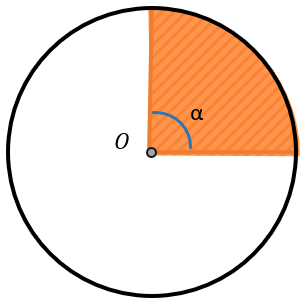
Если мы рассмотрим сектор, который занимает четверть от круга, получится, что его тоже будет являться четвертью от 360⁰
(frac{alpha}{360{^circ}} = frac{90{^circ}}{360{^circ}} = frac{1}{4})
Поэтому, для того чтобы найти площадь сектора, нужно найти площадь круга и умножите её на долю сектора, который на этот круг приходится:
(S = pi R^{2} bullet frac{alpha}{360{^circ}})
где (frac{alpha}{360⁰}) показывает, какую часть от круга занимает сектор
Площадь сектора круга равна произведению площади круга на отношение градусной меры дуги этого сектора к 360⁰.
(S = pi R^{2} bullet frac{alpha}{360{^circ}})