Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
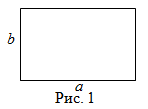
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней – 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ – 5 м.
Решение. Сделаем чертеж (рис. 2).
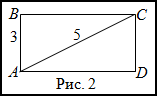
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Сегодня клоун Бим и дрессировщик Бом вместе с ребятами применяют на практике знания, как найти площадь для прямоугольника с разными сторонами.
Площадь фигуры — это размер куска плоскости внутри границ фигуры, измеренный в единицах измерения площади.
Единицы измерения площади — это площади квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
Определение. Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника.
Правило. Для вычисления площади прямоугольника (с разными сторонами), если известны длины его сторон, достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади. При необходимости результат укрупняют или раздробляют (см. Статью о переводе из одной единицы измерения площади в другую).
Содержание статьи:
Площадь — это?
Площадь любого куска плоскости (фигуры)— это размер этого куска плоскости (куска плоскости внутри границ фигуры), измеренный в единицах измерения площади.
Бим и Бом пришли на работу в цирк пораньше. Бим зашел к Бому в гримерку.
— Привет, Бим!
— Привет, Бом!
— У нашей Буфетчицы сегодня день рождения. Я купил очень вкусных конфет, только вот упаковка видишь какая длинная. У тебя есть какая-нибудь красивая коробка, куда мы можем сложить конфеты и подарить Буфетчице?
— У меня много разных красивых коробочек. Но как мы узнаем, какая из них подходит, чтобы вместились все конфеты и было красиво?
Бом и Бим задумались.
— Ура!!! Придумал, — нашелся Бим. — У каждой коробки есть плоское донышко. Давай вычислим площади донышек у каждой коробки, то есть измерим площадь донышек в единицах измерения площади — квадратных сантиметрах.
— Тогда найдем, какая коробка подходит больше всего, — подхватил Бом. — Начнем с упаковки, где лежат конфеты. У упаковки донышко в виде прямоугольника. Значит, достаточно измерить длины короткой и длинной стороны.
— А чем будем измерять? — задумался Бим.
— Сейчас поищу, — ответил Бом. — Вот у меня есть сантиметр, линейка и листочек в клеточку.
— Дай, пожалуйста, мне листочек в клеточку, — попросил Бом. — Я проверю, что донышко упаковки — прямоугольник.
Как найти площадь прямоугольника с разными сторонами. Площадь прямоугольника — это?
Определение. Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника.
Правило. Для вычисления площади прямоугольника, если известны длины его сторон, достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади. При необходимости результат можно укрупнить или раздробить (см. Статью о переводе из одной единицы измерения площади в другую).
Бим приложил листочек к углам донышка упаковки.
— Проверил: у упаковки четыре угла, и все они — прямые. Тогда донышко упаковки — прямоугольник.
Бом начал читать свои записи:
“Площадь прямоугольника — это размер куска плоскости, лежащего внутри границ прямоугольника. Как найти площадь прямоугольника (с разными сторонами), если известны длины его сторон? Достаточно перемножить длины двух прилежащих сторон. Результат записывается в единицах измерения площади”.
— Теперь надо измерить длины двух сторон. Упаковка — длинная, тогда лучше взять сантиметр.
Бим измерил упаковку.
— Короткая сторона 8 см, длинная — 72 см. Вспоминаем, что для вычисления площади прямоугольника надо длину одной стороны умножить на длину прилежащей стороны. Умножаем:
72 х 8 =576 кв.см (см2).
— Сейчас принесу из подсобки коробки, которые у меня есть, — побежал Бом.
И — надо же! — по дороге Бом встретил Олю, Колю и Васю, которые пришли пораньше на представление.
— Ребята, как хорошо, что вы здесь! Идемте, поможете нам с Бимом подобрать Буфетчице на день рождения коробку.
Бом достал из подсобки коробки, и они все вместе вернулись к Биму.
— Ребята, мы с Бимом измерили площадь упаковки конфет, которые мы хотим переложить в более красивую коробку. Красиво сложим и подарим Буфетчице на день рождения, — объяснил Бим.
— Давайте вычислим площадь донышка каждой коробки, — предложил Вася. — В коробку, у которой площадь донышка равна площади донышка упаковки, мы переложим конфеты.
— Как здорово, что Бом принес все коробки, донышки у которых имеют вид прямоугольника! — обрадовался Коля. — Как найти площадь прямоугольника с разными сторонами? Надо измерить длины двух прилежащих сторон в одинаковых единицах измерения длины и их перемножить, — получим площадь прямоугольника в единицах измерения площади. Для коробок удобнее всего измерять длины сторон в сантиметрах, а площадь самих прямоугольников уже будет в квадратных сантиметрах. Оля, давай проверим, что донышки коробок — прямоугольники.
Коля и Оля взяли листочек в клеточку и с помощью него проверили, что у донышек все углы прямые.
Затем Коля, Вася и Оля вооружились листочком в клеточку, линейкой и сантиметровой лентой и измерили в сантиметрах длины прилежащих сторон донышек коробок.
Первым управился Коля:
— У меня большая сторона 36 сантиметров и короткая 16 сантиметров. Получаем площадь моей коробки
36 х 16 = 576 (кв.см).
Следующим был Вася:
— У меня длина коробки 30 см, а ширина — 20 см. Для вычисления площади коробки надо длину умножить на ширину прямоугольника. Получаем:
30 х 20 = 600 (кв.см)
Оля измеряла тщательнее всех, ведь у нее коробка была похожа на квадрат. Но надо было убедиться, точно ли у этой коробки равны обе стороны. Так и оказалось:
— У меня прилежащие стороны одинаковые по длине, обе равны 24 см. Перемножаем длины двух прилежащих сторон, получаем: 24 х 24 = 576 (кв.см).
— Тогда у нас выходят 3 коробки с одинаковыми площадями донышек — у упаковки, — подытожил Бом:
8 х 72 = 576 (кв.см), —
и еще у двух коробок
16 х 36 = 576 (кв.см),
24 х 24 = 576 (кв.см),
а также одна коробка площадью больше, чем у упаковки
30 х 20 = 600 (кв.см).
— Какую же коробку выбрать? — озадаченно спросил Бим.
— Давай возьмем в виде квадрата, посмотрите какая здесь красивая крышка! — решил Бом.
Ребята выложили конфеты из упаковки в коробку.
— Ага, — посмотрел Бом. — получились три ряда. Какая же площадь донышка одного ряда? Длина ряда 24 см, ширина — 8 см. Значит площадь донышка одного ряда равна:
24 х 8 = 192 (кв.см).
Всего три одинаковых ряда
192 х 3 = 576 (кв.см).
Ура! Все совпадает!
Бим, все же, спросил:
— Сейчас мы измеряли площадь в квадратных сантиметрах. А какие еще есть единицы измерения площади?
Единицы измерения площади
Единицы измерения площади — это площадь квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м). (См. статью “Единицы измерения площади”)
В каких единицах измерения площади мы можем записать площадь донышка одного ряда? — продолжил вопрос Бим.
Оля ответила сразу:
— Если мы будем укрупнять, то в дециметрах и сантиметрах.
576 кв.см = 5 кв.дм 76 кв.см
— А если мы будем раздроблять — в миллиметрах, — добавил Коля. —
576 кв.см =576 х 100 (кв.мм).
А еще единицы измерения площади 1 кв.м (квадрат со стороною 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
— Теперь я подпишу открытку. У меня красивый артистический почерк, — вызвался Бом.
— Хорошо, Бом. А мы с ребятами составим вопросы и ответы на них, — согласился Бим.
— Первый вопрос: Что называется площадью? — начал Вася.
— Второй вопрос: Дайте определение прямоугольника. — продолжил Коля. —
И третий вопрос: Что такое площадь прямоугольника?
— Четвертый вопрос: Как найти площадь прямоугольника (с разными сторонами)? — закончила Оля.
— И еще один, пятый, вопрос: Какие вы знаете единицы измерения площади? — добавил Бим.
Теперь я запишу ответы для проверки, — продолжил клоун:
1. Площадь — это размер куска плоскости внутри фигуры.
2. Прямоугольник — это фигура с 4-мя прямыми углами и с замкнутой границей из четырех отрезков.
3. Площадь прямоугольника — это площадь куска плоскости внутри границ прямоугольника.
4. Как найти площадь прямоугольника? Для нахождения площади прямоугольника перемножаются длины двух прилежащих сторон. Результат записывается в единицах измерения площади.
5. Единицы измерения площади — это площади квадратов, у которых стороны равны либо единице измерения длины, либо 10 м, либо 100 м: 1 кв.мм (квадрат со стороной 1 мм), 1 кв.см (квадрат со стороной 1 см), 1 кв.дм (квадрат со стороной 1 дм), 1 кв.м (квадрат со стороной 1 м), 1 кв.км (квадрат со стороной 1 км), 1 ар (квадрат со сторонами 10 м), 1 га (квадрат со стороной 100 м).
Итог подвел Бом:
— Мы сегодня узнали :
- что такое площадь
- что такое площадь прямоугольника
- как найти площадь прямоугольника
- единицы измерения площади.
Всем спасибо за помощь.
Заключение
Итак, теперь мы знаем ответ на вопрос: Как найти площадь прямоугольника с разными сторонами. А вам приходилось дарить конфеты в коробочках? Как видим, можно, в случае чего, упаковать подарок более изящно, а заодно — и математику повторить.
Идея необычной подачи материала принадлежит замечательному преподавателю математики Стуловой Лилии Валериевне.
Ждём Ваши оценки и комментарии!)))
Как рассчитать площадь прямоугольника
На данной странице калькулятор поможет рассчитать площадь прямоугольника онлайн. Для расчета задайте длину сторон или длины диагоналей и угол между ними.
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Через стороны
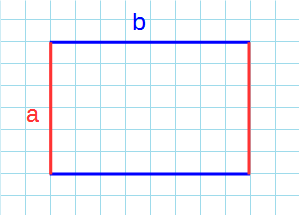
Формула для нахождения площади прямоугольника через стороны:
a, b – стороны прямоугольника.
Через диагонали и угол между ними
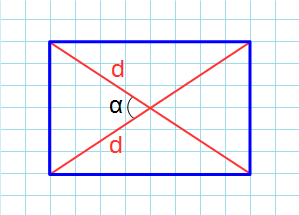
Формула для нахождения площади прямоугольника через диагонали и угол между ними:
d – диагональ; α – угол между диагоналями.
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.

Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.

Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.

S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.
