5.3.6. Как найти плоскость, перпендикулярную данной?
Очевидно, что к любой плоскости можно провести бесконечно много перпендикулярных плоскостей, и для того, чтобы зафиксировать конкретную перпендикулярную плоскость, нужно задать точку и вектор либо две точки:
Задача 142
Дана плоскость ![]() (координаты декартовы). Найти плоскость
(координаты декартовы). Найти плоскость ![]() , перпендикулярную данной и проходящую через точки
, перпендикулярную данной и проходящую через точки ![]() .
.
Решение начнём с вопроса задачи: что мы знаем о плоскости ![]() ?
?
Известны две точки. Можно найти вектор ![]() , параллельный данной плоскости. Маловато. Было бы неплохо раздобыть ещё один подходящий вектор. Так как плоскости должны быть перпендикулярны, то подойдёт нормальный вектор
, параллельный данной плоскости. Маловато. Было бы неплохо раздобыть ещё один подходящий вектор. Так как плоскости должны быть перпендикулярны, то подойдёт нормальный вектор ![]() плоскости
плоскости ![]() (для лучшего понимания задачи отложите вектор нормали
(для лучшего понимания задачи отложите вектор нормали ![]() от точки
от точки ![]() в плоскости
в плоскости ![]() ).
).
Проводить подобные рассуждения здОрово помогает схематический чертёж! – повторю этот красный, а точнее, золотой совет 🙂 Итак, задача «раскручена», и решение удобно оформить по пунктам (это совет серебряный:):
1) Найдём вектор ![]() .
.
2) Из уравнения ![]() снимем вектор нормали:
снимем вектор нормали: ![]() .
.
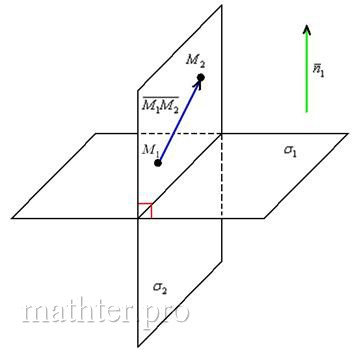
3) Уравнение плоскости ![]() составим по точке
составим по точке ![]() (можно взять
(можно взять ![]() ) и двум неколлинеарным векторам
) и двум неколлинеарным векторам ![]() :
:
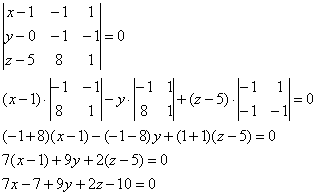
Ответ: ![]()
Проверка состоит из двух этапов:
1) Проверяем, действительно ли плоскости будут перпендикулярны. Если две плоскости перпендикулярны, то их векторы нормали будут ортогональны. Логично. Из полученного уравнения ![]() снимаем вектор нормали
снимаем вектор нормали ![]() и рассчитываем скалярное произведение векторов:
и рассчитываем скалярное произведение векторов:
![]() , а значит,
, а значит, ![]()
К слову, здесь мы разобрали ещё одну задачу – проверили плоскости на перпендикулярность, и теперь вы знаете, как это сделать.
2) В уравнение плоскости ![]() подставляем координаты точек
подставляем координаты точек ![]() . Обе точки должны «подойти».
. Обе точки должны «подойти».
И первый, и второй пункт можно выполнить устно. Но выполнить обязательно! И это уже даже не платиновый совет – это аксиома!
…Что-то не хочется мне вас сегодня отпускать…, наверное, хорошо себя вели и добросовестно прорешали все задачи =) Придётся рассказать что-нибудь ещё:
 5.3.7. Взаимное расположение трёх плоскостей
5.3.7. Взаимное расположение трёх плоскостей
 5.3.5. Как найти угол между плоскостями?
5.3.5. Как найти угол между плоскостями?
| Оглавление |
Автор: Aлeксaндр Eмeлин
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
Пусть
в трехмерном пространстве задана
прямоугольная декартова система
координат. Сформулируем следующую
задачу:
Составить
уравнение плоскости, проходящей через
данную точку
M(x0,
y0,
z0) перпендикулярно
данному вектору
n =
{A, B, C}
.
Решение. Пусть P(x, y, z)
— произвольная точка пространства.
Точка P принадлежит
плоскости тогда и только тогда, когда
вектор
MP =
{x − x0, y − y0, z − z0}
ортогонален вектору n =
{A, B, C}
(рис.1).

Написав
условие ортогональности этих векторов
(n, MP)
= 0 в координатной форме, получим:
|
A(x − x0) |
Уравнение
плоскости по трем точкам
В
векторном виде
![]()
В
координатах

Взаимное
расположение плоскостей в пространстве
Пусть
![]() и
и ![]()
– общие уравнения двух
плоскостей. Тогда:
1)
если ![]() ,
,
то плоскости совпадают;
2)
если ![]() ,
,
то плоскости параллельны;
3)
если ![]() или
или ![]() ,
,
то плоскости пересекаются и системауравнений
![]() (6)
(6)
является
уравнениями прямой пересечения данных
плоскостей.
3.3

Решение:
Ответ: |
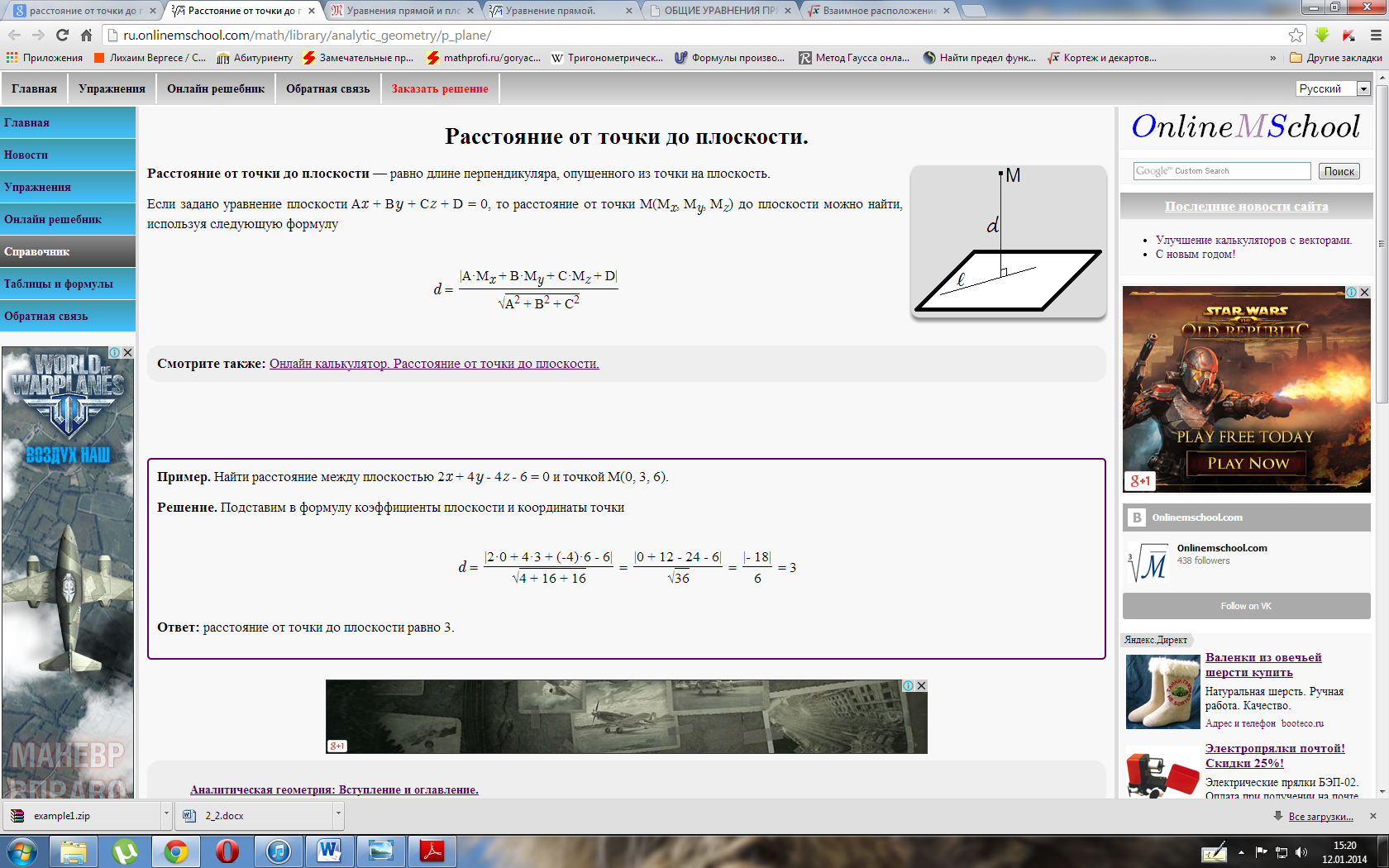
Берём |
Составить
параметрические уравнения следующих
прямых:


Решение:
Прямые заданы каноническими уравнениями
и на первом этапе следует найти
какую-нибудь точку, принадлежащую
прямой, и её направляющий вектор.
а)
Из уравнений ![]() снимаем
снимаем
точку и направляющий вектор: ![]() .
.
Точку можно выбрать и другую (как это
сделать – рассказано выше), но лучше
взять самую очевидную. Кстати, во
избежание ошибок, всегда подставляйте
её координаты в уравнения.
Составим
параметрические уравнения данной
прямой:

Удобство
параметрических уравнений состоит в
том, что с их помощью очень легко находить
другие точки прямой. Например, найдём
точку ![]() ,
,
координаты которой, скажем, соответствуют
значению параметра ![]() :
:

Таким
образом: ![]()
б)
Рассмотрим канонические уравнения ![]() .
.
Выбор точки здесь несложен, но
коварен: ![]() (будьте
(будьте
внимательны, не перепутайте координаты!!!).
Как вытащить направляющий вектор? Можно
порассуждать, чему параллельна данная
прямая, а можно использовать простой
формальный приём: в пропорции находятся
«игрек» и «зет», поэтому запишем
направляющий вектор ![]() ,
,
а на оставшееся место поставим ноль: ![]() .
.
Составим
параметрические уравнения прямой:

в)
Перепишем уравнения ![]() в
в
виде ![]() ,
,
то есть «зет» может быть любым. А если
любым, то пусть, например, ![]() .
.
Таким образом, точка ![]() принадлежит
принадлежит
данной прямой. Для нахождения направляющего
вектора используем следующий формальный
приём: в исходных уравнениях ![]() находятся
находятся
«икс» и «игрек», и в направляющем векторе
на данных местах записываем нули: ![]() .
.
На оставшееся место ставим единицу: ![]() .
.
Вместо единицы подойдёт любое число,
кроме нуля.
Запишем
параметрические уравнения прямой:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнение плоскости через координаты вектора нормали и точки: онлайн-калькулятор
Плоскость — это бесконечная поверхность с принадлежащими ей прямыми, через которые проходят любые две ее точки. Нормалью к кривой в указанной точке является прямая, расположенная перпендикулярно к касательной прямой в заданной точке кривой.
Если указаны координаты точки A(x1,y1,z1), принадлежащей плоскости, и вектор нормали n={A,B,C}, то уравнение плоскости соответствует формуле:
A(x-x1)+B(y-y1)+C(z-z1)=0.
Чтобы найти уравнение плоскости, перпендикулярной вектору онлайн, необходимо:
- указать значение точки A;
- заполнить значение вектора;
- воспользоваться кнопкой «Рассчитать».
Уравнение плоскости через точку перпендикулярно вектору онлайн
Сервис предназначен для геометрических вычислений, которыми пользуются учащиеся школ и студенты университетов для подготовки к занятиям.
Решение задачи с помощью онлайн-калькулятора имеет преимущества:
- формула в основе автоматических подсчетов дает точный ответ без ошибок и опечаток;
- нет необходимости искать нужный способ расчета;
- пользователю доступно подробное решение;
- производить расчеты можно неограниченное количество раз бесплатно.
Пошаговые вычисления позволяют учащемуся вникнуть в процесс решения задачи по геометрии и справляться с заданиями самостоятельно. Подготовка к занятиям благодаря калькулятору занимает меньше времени и происходит более продуктивно.
Уравнения плоскости, проходящей через точку перпендикулярно вектору
Общее уравнение плоскости
Ненулевой вектор , перпендикулярный заданной плоскости, называется нормальным вектором (или, короче, нормалью) для этой плоскости.
Пусть в координатном пространстве (в прямоугольной системе координат) заданы:
а) точка ;
б) ненулевой вектор (рис.4.8,а).
Требуется составить уравнение плоскости, проходящей через точку перпендикулярно вектору
Выберем в пространстве произвольную точку . Обозначим
— радиус-векторы точек
и
Точка
принадлежит заданной плоскости тогда и только тогда, когда векторы
и
перпендикулярны (рис.4.8,б). Условие ортогональности запишем при помощи скалярного произведения:
Учитывая, что , получаем векторное уравнение плоскости:
(4.12)
Это уравнение можно записать в другой форме. Преобразуем левую часть используя свойства скалярного произведения. Обозначая
получаем уравнение
или
(4.13)
выражающее постоянство проекций на нормаль радиус-векторов точек, принадлежащих плоскости.
Получим координатную форму записи векторного уравнения плоскости (4.12). Так как
формуле (1.10) находим
(4.14)
Полученное соотношение (4.14) позволяет по координатам точки и координатам
нормали
сразу записать искомое уравнение плоскости.
Обозначив , получим общее уравнение плоскости
(4.15)
Поскольку коэффициенты не равны нулю одновременно (это координаты ненулевого вектора
), уравнение (4.15) является алгебраическим уравнением первой степени, т.е. линейным уравнением с тремя неизвестными. Следовательно, плоскость является алгебраической поверхностью первого порядка.
Проводя рассуждения в обратном порядке, делаем вывод о том, что линейное уравнение (4.15) задает в координатном пространстве плоскость. Полученные выводы сделаны для прямоугольной системы координат, но, учитывая теорему 4.1, они переносятся (без изменений) и на любую аффинную систему координат.
Теорема (4.2) об алгебраической поверхности первого порядка
Всякое уравнение первой степени с тремя неизвестными задает в аффинной системе координат плоскость, и наоборот, всякая плоскость в любой аффинной системе координат может быть задана уравнением первой степени с тремя неизвестными. Другими словами, алгебраическая поверхность первого порядка есть плоскость.
Замечания 4.2.
1. При составлении общего уравнения плоскости нормаль выбирается неоднозначно: можно выбрать любую, отличную от нуля, длину нормали а также одно из двух возможных направлений (противоположный вектор
также является нормалью). Например, вместо нормали
можно взять нормаль
что соответствует умножению обеих частей уравнения (4.15) на число –7.
2. Если в общем уравнении плоскости (4.15) коэффициент при неизвестной равен нулю, то плоскость параллельна координатной оси. Например, если то плоскость (4.15) параллельна оси абсцисс
(рис.4.9,а); если
то плоскость (4.15) параллельна координатным осям
и
т.е. параллельна координатной плоскости
(рис.4.9,б).
Если в общем уравнении плоскости (4.15) свободный член равен нулю то плоскость проходит через начало координат (рис.4.9,в).
3. Нормаль к плоскости
совпадает с градиентом функции
В курсе математического анализа доказывается, что градиент направлен в сторону наискорейшего возрастания функции в данной точке.
4. Плоскость разбивает пространство на два полупространства (рис.4.10): положительное, координаты всех точек которого удовлетворяют неравенству
и отрицательное, для точек которого
Нормаль
приложенная к произвольной точке плоскости
указывает на положительное полупространство (рис.4.10).
Это свойство следует из пункта 3.
5. Абсолютное значение пропорционально расстоянию от точки
до плоскости
т.е. отношение расстояний от точек
и
до плоскости
равно отношению
Доказательство аналогично доказательству пункта 5 замечаний 3.2.
6. В аффинной системе координат линейное уравнение
задает, согласно теореме 4.2, плоскость. Выводы, полученные в п.2,3,4,5, остаются справедливыми с тем лишь исключением, что вектор
не является нормалью.
Пример 4.5. В координатном пространстве (в прямоугольной системе координат) заданы точки
и
Составить уравнение плоскости, перпендикулярной отрезку
и проходящей через его середину (рис.4.11).
Решение. Находим координаты середины отрезка
т.е.
Вектор
можно взять в качестве нормали к плоскости. Находим координаты этого вектора, вычитая из координат его конца соответствующие координаты его начала:
Следовательно, уравнение (4.15) искомой плоскости имеет вид
Осталось найти величину свободного члена . Поскольку точка
принадлежит плоскости, то ее координаты
должны удовлетворять уравнению этой плоскости, следовательно,
отсюда
Таким образом, искомая плоскость задается уравнением
Уравнение этой прямой можно было получить в виде (4.14), подставляя координаты нормали и точки
Расстояние от точки до плоскости
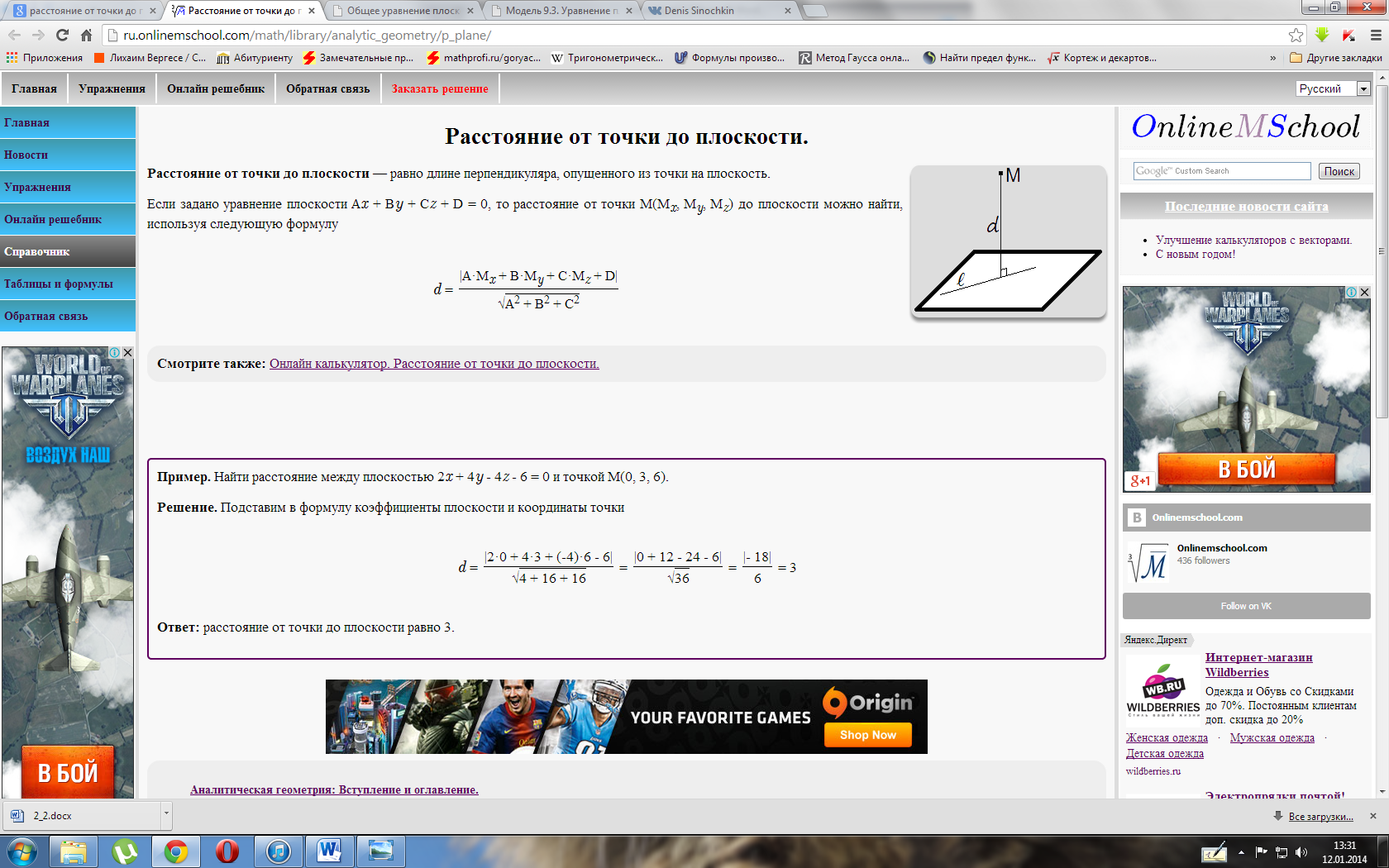
Пусть заданы:
а) плоскость, описываемая общим уравнением (4.15): ;
б) точка в пространстве.
Требуется найти расстояние от точки до плоскости.
Искомое расстояние равняется длине ортогональной проекции вектора на направление нормали
(рис.4.12) и находится по формуле:
,
где — любая точка на заданной плоскости.
Запишем правую часть в координатной форме, выражая скалярное произведение и длину через координаты векторов
Поскольку координаты точки удовлетворяют уравнению (4.15), то
Подставляя это выражение, получаем формулу расстояния от точки до плоскости
(4.16)
Пример 4.6. В координатном пространстве (в прямоугольной системе координат) заданы точки
и
Требуется найти, в каком отношении плоскость
делит отрезок
(рис.4.13).
Решение. Найдем значения линейного четырехчлена в точках
и
и
Получили значения разных знаков. Следовательно, точки и
лежат по разные стороны от плоскости я (согласно пункту 4 замечаний 4.2, эти точки лежат в разных полупространствах), т.е. плоскость
действительно пересекает отрезок
(в точке
на рис.4.13). Так как эти значения по абсолютной величине пропорциональны расстояниям от точек
и
до плоскости
, то
Этот же результат можно получить по формуле (4.16). Находим расстояния и
от точек
и
до плоскости
Следовательно,
Нормированное уравнение плоскости
Преобразуем общее уравнение плоскости следующим образом. Если свободный член
то разделим обе части на длину нормали
а если
то разделим на
Коэффициенты при неизвестных при этом станут равными направляющим косинусам нормали:
а свободный член , в силу описанного выбора знака, будет неположительным. Обозначим его через
Тогда получим нормированное уравнение плоскости
(4.17)
Замечания 4.3.
1. Свободный член нормированного уравнения (4.17) равен расстоянию от начала координат до плоскости. Это следует из формулы (4.16).
2. Нормированное уравнение плоскости (4.17) можно записать в виде (4.13): если в качестве нормали
вы брать единичный вектор
так как
Из двух возможных единичных нормалей условию
отвечает нормаль
направленная к плоскости (рис.4.14), если вектор
приложить к началу координат. При выборе противоположного вектора
получилось бы отрицательное значение
которое не допускается в уравнении (4.17).
3. Коэффициенты общего уравнения плоскости (4.15) определяются неоднозначно в силу неоднозначного выбора нормали (см. пункт 1 замечаний 4.2). При составлении нормированного уравнения (4.17) плоскости такого произвола нет. Здесь все коэффициенты определены однозначно (при ) или с точностью до знака (при
4. Нормированное уравнение плоскости имеет смысл только в прямоугольной системе координат.
Пример 4.7. В координатном пространстве (в прямоугольной системе координат) заданы точки
и
(см. рис.4.11). Требуется:
а) составить нормированное уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;
б) найти расстояние от начала координат до этой плоскости.
Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: Найдем длину нормали
Так как свободный член отрицательный, разделим уравнение на
Нормированное уравнение плоскости получено.
б) По нормированному уравнению определяем расстояние от начала координат до плоскости (см. пункт 1 замечаний 4.3).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Уравнение плоскости перпендикулярной плоскости xoy
Если A = B = 0, т. е. уравнение имеет вид Cz + D = 0, или .
то вектор нормали коллинеарен вектору k = (0, 0, 1). Поэтому плоскость перпендикулярна оси OZ, а значит параллельна плоскости XOY. Координатная плоскость XOY имеет уравнение z = 0.
Аналогично, x = 0 — уравнение координатной плоскости YOZ; x = а — уравнение плоскости, параллельной YOZ; y = 0 — уравнение плоскости XOZ; y = b — уравнение плоскости, параллельной XOZ.
Если равна нулю только одна из координат вектора нормали, то нормаль перпендикулярна, а плоскость, следовательно, параллельна соответствующей оси. Например, плоскость Ax + Cz + D = 0 параллельна оси OY (возможно, содержит эту ось).
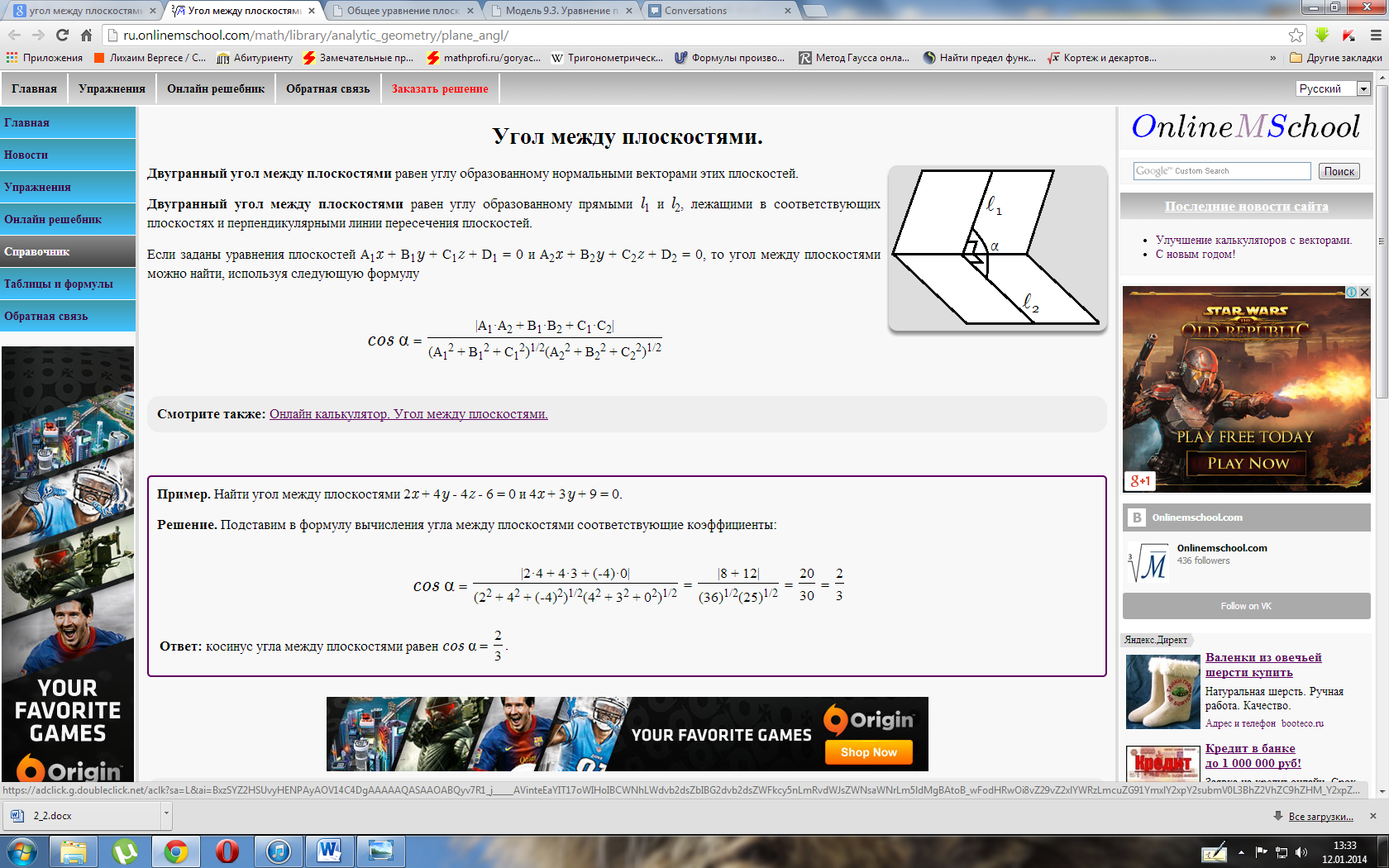
Вопросы о взаимном расположении плоскостей решаются с помощью вектора нормали. Пусть две плоскости заданы своими уравнениями: A1x + B1y + C1z + D1 = 0 (плоскость P1), A2x + B2y + C2z + D2 = 0 (плоскость P2).
Запишем в краткой, символической форме условия параллельности и перпендикулярности плоскостей:
Угол между плоскостями равен углу между векторами нормали и находится с помощью скалярного произведения (см. раздел 4.2).
Пример 9. Найти угол между плоскостями 2x — 2y + z — 5 = 0, x — z + 7 = 0.
Решение. Найдём косинус угла между векторами нормали N1 = (2, —2, 1) и N2 = (1, 0, —1):
Используя таблицы или калькулятор, можно найти.
Как известно, через любые 3 точки, не лежащие на одной прямой, можно провести единственную плоскость. Научимся решать эту важную задачу в общем виде, а затем рассмотрим пример.
Пусть точки M1(x1, y1,z1), M2(x2,y2,z2), M3(x3,y3,z3) не лежат на одной прямой. Мы помним, что главное для записи уравнения плоскости — найти вектор нормали, т. е. какой-нибудь вектор, перпендикулярный плоскости. В качестве такого вектора можно взять векторное произведение:
Общее уравнение плоскости
В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.
Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:
где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.
Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.
Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.
Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.
Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.
Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x0, y0, z0. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y0, z0. Тогда
 .
.
Таким образом, существует точка M0(x0, y0, z0), координаты которой удовлетворяют уравнению (1):
Вычитая из уравнения (1) тождество (2), получим
| A(x−x0)+B(y−y0)+С(z−z0)=0, | (3) |
которая эквивалентна уравнению (1).
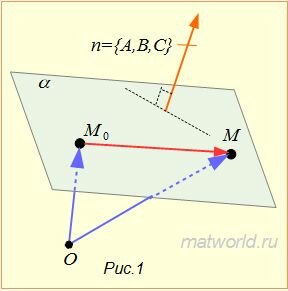
Покажем, что (3) определяет некоторую плоскость, проходящую через точку M0(x0, y0, z0) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).
Если точка M0(x0, y0, z0) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и  перпендикулярны (Рис.1) и их скалярное произведение равно нулю:
перпендикулярны (Рис.1) и их скалярное произведение равно нулю:
Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и  не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.
не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.
Одновременно с доказательством теоремы 1 мы получили следующее утверждение.
Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.
Вектор n=(A,B,C) называется нормальным вектором плоскости , определяемой линейным уравнением (1).
Утверждение 2. Если два общих уравнения плоскости
определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства
| A2=A1λ, B2=B1λ, C2=C1λ, D2=D1λ. | (6) |
Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:
(A1λ−A2)x0+(B1λ−B2)y0+(C1λ−C2)z0+(D1λ−D2)=0.
Так как выполнены первые три равенства из выражений (6), то D1λ−D2=0. Т.е. D2=D1λ. Утверждение доказано.
Неполные уравнения плоскости
Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .
Рассмотрим все возможные варианты неполных уравнений плоскости:
При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.
При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.
При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).
При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).
При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).
При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).
При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).
При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).
При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).
При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).
Рассмотрим примеры построения общего уравнения плоскости.
Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.
Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x0,y0,z0) имеет вид (3). Подставляя координаты точки M в (3), получим:
| A(x−4)+B(y−(−1))+C(z−2)=0 | (9) |
Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=<0,0,1>, т.е. A=0, B=0, C=1.
Подставляя коэффициенты A,B,C в (9), получим:
| 0(x−4)+0(y−(−1))+1(z−2)=0 | (9) |
Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==<2,3,1>.
Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x0,y0,z0) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:
| A(x−0)+B(y−0)+C(z−0)=0 | (10) |
Так как плоскость имеет нормальный вектор n=<A,B,C>=<2,3,1>, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:
| 2(x−0)+3(y−0)+1(z−0)=0 | (9) |
Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.
1.3.2. Аналитическая геометрия в пространстве
1. Всякая плоскость в координатном пространстве OXYZ имеет векторное уравнение следующего вида: r ¦ п = p. Здесь
r = xi + yj + zk — радиус-вектор текущей точки плоскости
M(x, у, z); п = i cosa + j cos b + k cosg — единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат, a, b, g — углы, образованные этим перпендикуляром с осями координат OX, OY, OZ, и р — длина этого перпендикуляра.
При переходе к координатам это уравнение принимает вид xcos a + ycos b + zcos g – p = 0 (нормальное уравнение плоскости).
2. Уравнение всякой плоскости может быть записано также в виде Ах + Ву +Cz + D = 0 (общее уравнение). Здесь А, B, C можно рассматривать как координаты некоторого вектора
N = Ai + Bj + Ck, перпендикулярного к плоскости. Для приведения общего уравнения плоскости к нормальному виду все члены уравнения надо умножить на нормирующий множитель
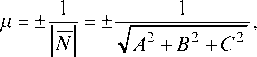
где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.
3. Частные случаи расположения плоскости, определяемой уравнением Ах + Ву +Cz + D = 0:
А = 0; плоскость параллельна оси ОХ;
В = 0; плоскость параллельна оси О^
C = 0; плоскость параллельна оси ОZ;
D = 0; плоскость проходит через начало координат;
А = В = 0; плоскость перпендикулярна оси ОZ (параллельна плоскости ХОY);
А = C = 0; плоскость перпендикулярна оси ОY (параллельна плоскости ХОZ);
В = C = 0; плоскость перпендикулярна оси ОХ (параллельна плоскости YОZ);
А = D = 0; плоскость проходит через ось ОХ;
В = D = 0; плоскость проходит через ось OY;
C = D = 0; плоскость проходит через ось OZ;
А = В = D = 0; плоскость совпадает с плоскостью XOY (z = 0);
А = C = D = 0; плоскость совпадает с плоскостью XOZ (у = 0);
B = C = D = 0; плоскость совпадает с плоскостью YOZ (х = 0).
Если в общем уравнении Ах + By +Cz + D = 0 коэффициент D ф 0, то, разделив все члены уравнения на – D, можно уравнение
плоскости привести к виду ^ здесь
^ здесь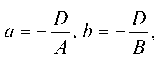
. Это уравнение плоскости называется уравнением в отрезках: в нем а — абсцисса точки пересечения плоскости с осью OX, b и с — соответственно ордината и аппликата точек пересечения плоскости с осями OY и OZ.
4. Угол j между плоскостями А1х + В1У + Qz + D1 = 0 и А2х + В2У +C2z + D2 = 0 определяется по формуле

Условие параллельности плоскостей:

Условие перпендикулярности плоскостей:

5. Расстояние от точки М0(х0; у0; z0) до плоскости, определяемой уравнением Находится по формуле
Находится по формуле


Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости; знак результата этой подстановки характеризует взаимное расположение точки M0 и начала координат относительно данной плоскости: этот знак положителен, если точка M0 и начало координат расположены по разные стороны от плоскости, и отрицателен, если они расположены по одну сторону от плоскости.
6. Уравнение плоскости, проходящей через точку М0(х0; у0; z0)
и перпендикулярной к вектору N = Ai + Bj + Ck, имеет вид А(х – х0) + B(y – у0) + C(z – z0) = 0. При произвольных А, В и C последнее уравнение определяет некоторую плоскость, принадлежащую к связке плоскостей, проходящих через точку М0. Его часто поэтому называют уравнением связки плоскостей.
7. Уравнение А1х + B1y +C1z + D1 + А(А2х + B^y +C2z + D2) = 0 при произвольном I определяет некоторую плоскость, проходящую через прямую, по которой пересекаются плоскости, определяемые уравнениями


некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую (в силу чего такое уравнение часто называют уравнением пучка плоскостей). Если плоскости, определяемые уравнениями I и II, параллельны, то пучок плоскостей превращается в совокупность плоскостей, параллельных этим плоскостям.
8. Уравнение плоскости, проходящей через три заданные точки M1(r 1Х M1(Jj), M3(r 3) (Л = x1i + yd + z1k; r2 = x2i + У2 j + z2k; r3 = x3i + y3 j + z3 к), проще всего найти из условия компланарности векторов r – T1, r2 – rl, r3 – rl, где r = xi + yj+zk — радиус-вектор текущей точки искомой плоскости M:
или в координатной форме:


Пример 1.21. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + у + 5z – 1 = 0, 2x + 3у – z + 2 = 0 и через точку М(3, 2, 1).
Решение. Воспользуемся уравнением пучка плоскостей

Значение I определяем из условия, что координаты точки М должны удовлетворять этому уравнению:

Получаем искомое уравнение в виде:
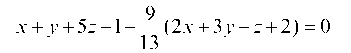
или, умножая на 13 и приводя подобные члены, в виде:

Пример 1.22. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + 3у + 5z – 4 = 0 и X – у – 2z + 7 = 0 и параллельной оси оу.
Решение. Воспользуемся уравнением пучка x + 3у + 5z – 4 + + l(x – у – 2z + 7) = 0, преобразуем уравнение к виду (1 + Х)х + (3 -1)у + (5 – 2l)z + (71 – 4) = 0.
Так как искомая плоскость параллельна оси ординат, то коэффициент при у должен равняться нулю, т. е. 3 – l = 0, I = 3. Подставив значение I в уравнение пучка, получаем

Пример 1.23. Найти уравнение плоскости, проходящей через точки М (2; -1; 4) и N(3; 2; -1) перпендикулярно к плоскости X + у + z – 3 = 0.
Решение. Воспользуемся уравнением плоскости, проходящей через первую из данных точек:

Условие прохождения этой плоскости через вторую точку и условие перпендикулярности определяются равенствами:

Исключая коэффициенты А, В и C из системы уравнений

получаем искомое уравнение в виде:


Пример 1.24. Из точки P(2; 3; -5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Решение. Основаниями перпендикуляров, опущенных на координатные плоскости, будут следующие точки М1(2; 3; 0), М2(2; 0; -5), М3(0; 3; -5). Напишем уравнение плоскости, проходящей через точки М1, М2, М3, для чего воспользуемся уравнением



Пример 1.25. Составить уравнение плоскости, проходящей через точку M (2; 3; 5) и перпендикулярной к вектору
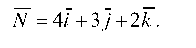
Решение. Достаточно воспользоваться уравнением плоскости, проходящей через данную точку и перпендикулярной к данному вектору:

1. Прямая может быть задана уравнениями 2-х плоскостей

пересекающихся по этой прямой.
2. Исключив поочередно х и у из предыдущих уравнений, получим уравнения х = аz + с, у = bz + d. Здесь прямая определена двумя плоскостями, проектирующими ее на плоскости хoz и yoz.
3. Если даны две точки M(x1, у1, z1) и N(x2, у2, z2), то уравнения прямой, проходящей через них, будут иметь вид:

4. Так называемые канонические уравнения
определяют прямую, проходящую через точку M(x1, у1, z1)
и параллельную вектору S = li + mj + nk. В частности, эти уравнения могут быть записаны в виде:


где a, b и g — углы, образованные прямой с осями координат.

5. От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям прямой:

6. Угол между двумя прямыми, заданными их каноническими


деляется по формуле
перпендикулярности двух прямых:


условие параллельности двух прямых:

7. Необходимое и достаточное условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):

Если величины /1, т, П1 непропорциональны величинам /2, m2, «2, то указанное соотношение является необходимым и достаточным условием пересечения двух прямых в пространстве.
условие параллельности прямой и плоскости: 

 условие перпендикулярности прямой и плоскости:
условие перпендикулярности прямой и плоскости:


 Определяется по формуле
Определяется по формуле

9. Для определения точки пересечения прямой
 С плоскостью Ах + Ву + Cz + D = 0 нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой x = /t + X0, у = mt + у0, z = nt + z0:
С плоскостью Ах + Ву + Cz + D = 0 нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой x = /t + X0, у = mt + у0, z = nt + z0:
а) если А/ + Вт + Cn ф 0, то прямая пересекает плоскость в одной точке;
б) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D ф 0, то прямая параллельна плоскости;
в) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D = 0, то прямая лежит в плоскости.
Пример 1.26. Привести к каноническому виду уравнения прямой 2х – у + 3z – 1 = 0 и 5х + 4у – z – 7 = 0.
Решение. Исключив вначале у, а затем z, получим:
Если разрешим каждое из уравнений относительно х, то будем иметь:
отсюда
Второй способ: найдем вектор S = li + mj + nk, параллельный искомой прямой. Так как он должен быть перпендикулярен к нормальным векторам заданных плоскостей N1 = 2i – j + 3k и N2= 5i + 4 j – k, то за него можно принять векторное произведение векторов N1 и N2.

Таким образом, l = -11; m = 17; n = 13.
За точку M1(x1, у1, z1), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью yoz. Т ак как при этом x1 = 0, то координаты y1 и z1 этой точки определятся из системы уравнений заданных плоскостей, если в них положить х = 0:
Решая эту систему, находим у1 = 2; z1 = 1.
Итак, искомая прямая определяется уравнениями:

Мы получили прежний ответ.
Пример 1.27. Построить прямую



Решение. Искомую прямую можно построить как линию пересечения плоскостей. Для этого напишем уравнения плоскостей, которыми определена прямая, в отрезках на осях:

Пример 1.28. Из начала координат опустить перпендикуляр на прямую

Решение. Составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой: 2х + 3у + z = 0. (Для этой плоскости можно принять А = l; B = m; C = n; D = 0; использовано условие перпендикулярности прямой и плоскости, см. п. 8 введения к настоящему разделу).
Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой имеют вид:

Построив данные плоскости, мы получим искомую прямую как линию пересечения этих плоскостей (рис. 20).
Для определения t имеем уравнение:


Остается составить уравнения прямой, проходящей через начало координат и через точку М (см. п. 3 введения к настоящему разделу):

Пример 1.29. В уравнениях прямой Определить
Определить
параметр n так, чтобы эта прямая пересекалась с прямой
 , и найти точку их пересечения.
, и найти точку их пересечения.
Решение. Для нахождения параметра n используем условие пересечения 2-х прямых:



Следовательно, уравнения пересекающихся прямых таковы: искомой:


Для вычисления координат точки пересечения этих прямых выразим из первого уравнения х и у через z: х = 2z, у = -3z. Подставляя их значения в равенство Имеем
Имеем ,
,
отсюда z = 1. Зная z, находим х и у: х = 2z = 2, у = -3z = -3. Следовательно M(2; -3; 1).
Пример 1.30. Прямая задана каноническими уравнениями

Составить общие уравнения этой прямой.
Решение. Канонические уравнения прямой можно записать в виде системы двух независимых уравнений:

Получили общие уравнения прямой, которая теперь задана пересечением 2-х плоскостей, одна из которых 5х – 3у – 13 = 0 параллельна оси Oz, а другая х + 3z – 11 = 0 параллельна оси Oy.
Пример 1.31. Найти координаты точки M, делящей попалам отрезок прямой

заключенный между плоскостями хoz и xoy.
Решение. Найдем точку А пересечения прямой с плоскостью хoz, полагая в уравнениях прямой у = 0. Тогда получим:
отсюда x = 2,6; z = 2,8. Тогда А(2,6; 0; 2,8).


отсюда X = 11, у = 14, или В(11; 14; 0).
Определяем координаты точки М, делящей отрезок АВ пополам:

Следовательно, координаты искомой точки М будут: М(6,8; 7; 1,4).
Пример 1.32. Составить уравнение плоскости, проходящей через прямую


Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:

которое делим на а ф 0, и пусть b /а = I:

Аналогично, полагая в уравнениях прямой z = 0, найдем координаты точки В пересечения прямой с плоскостью хоу:
В этом пучке нужно выбрать плоскость, параллельную 2-й данной прямой. Из условия параллельности плоскости и прямой, имеем:




Подставляя I = 1 в уравнение пучка плоскостей, получим:  Тогда искомое уравнение плоскости будет:
Тогда искомое уравнение плоскости будет:

Пример 1.33. Дана прямая  Найти ее проекцию на плоскость
Найти ее проекцию на плоскость
Решение. Нужно найти плоскость, которая проходит через данную прямую перпендикулярно к данной плоскости; тогда искомая проекция определится как пересечение этой плоскости с данной.
Составим уравнение пучка плоскостей, проходящих через данную прямую:
Эта плоскость должна быть перпендикулярной к данной плоскости, что можно записать как:
Тогда уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости, будет:
Проекция данной прямой на данную плоскость определяется как прямая пересечения плоскостей:

Запишем эту прямую в каноническом виде. Найдем на прямой какую-либо точку. Для этого положим, например х0 = 1, и система запишется в виде:

Отсюда, у0 = 1, z0 = 0, т. е. точка M(1; 1; 0) принадлежит искомой прямой.
Направляющий вектор прямой S = (l; m; n) найдем из того условия, что он перпендикулярен нормальным векторам
N1 = (2; -3; -2) и N2 = (5; 2; 2) плоскостей, определяющих искомую прямую.
В качестве S берем векторное произведение векторов N1 и N2 , т. е.

Тогда искомое уравнение в каноническом виде будет:
[spoiler title=”источники:”]
http://matworld.ru/analytic-geometry/obshchee-uravnenie-ploskosti.php
http://matica.org.ua/metodichki-i-knigi-po-matematike/a-s-shapkin-zadachi-po-vysshei-matematike-teorii-veroiatnostei-matematicheskoi-statistike-matematicheskomu-programmirovaniiu-s-resheniiami/1-3-2-analiticheskaia-geometriia-v-prostranstve
[/spoiler]


