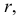В данной публикации мы рассмотрим, как можно найти площадь шара (сферы) и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади шара/сферы
- 1. Через радиус
- 2. Через диаметр
-
Примеры задач
Формула вычисления площади шара/сферы
1. Через радиус
Площадь (S) поверхности шара/сферы равняется произведению четырех его радиусов в квадрате и число π.
S = 4 π R2
Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
Как известно, диаметр шара/сферы равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь поверхности фигуры можно, используя такой вид формулы:
S = 4 π (d/2)2
Примеры задач
Задание 1
Вычислите площадь поверхности шара, если его радиус составляет 7 см.
Решение:
Воспользуемся первой формулой (через радиус):
S = 4 ⋅ 3,14 ⋅ (7 см)2 = 615,44 см2.
Задание 2
Площадь поверхности сферы равна 200,96 см2. Найдите ее диаметр.
Решение:
Выведем величину диаметра из соответствующей формулы расчета площади:
Шаром называют множество точек, удаленных от произвольно выбранной точки (центра шара) на расстояние не превышающее RR — радиус этого шара.
Онлайн-калькулятор площади поверхности шара
У шара, как и у круга, есть диаметр DD, который по длине в два раза превосходит радиус шара.
D=2⋅RD=2cdot R
Площадь поверхности шара можно найти используя как радиус, так и диаметр шара.
Формула площади поверхности шара по радиусу шара
S=4⋅π⋅R2S=4cdotpicdot R^2
RR — радиус шара.
Шар вписан в куб, диагональ которого dd равна 300sqrt{300} (см.). Найти площадь поверхности шара.
Решение
d=300d= sqrt{300}
Первым шагом в решении задачи будет нахождение длины стороны куба. Обозначим ее через aa. Тогда, по теореме Пифагора:
d2=a2+a2+a2d^2=a^2+a^2+a^2
d2=3⋅a2d^2=3cdot a^2
a=d3a=frac{d}{sqrt{3}}
a=3003=100=10a=frac{sqrt{300}}{sqrt{3}}=sqrt{100}=10
Радиус шара, вписаного в куб равен половине стороны этого куба:
R=a2=102=5R=frac{a}{2}=frac{10}{2}=5
Тогда площадь поверхности шара:
S=4⋅π⋅R2=4⋅π⋅52≈314S=4cdotpicdot R^2=4cdotpicdot 5^2approx314 (см. кв.)
Ответ: 314 см. кв.
Формула площади поверхности шара по диаметру шара
Формулу для площади поверхности шара легко получить через его диаметр, пользуясь соотношением между радиусом и диаметром шара:
S=4⋅π⋅R2=4⋅π⋅(D2)2=π⋅D2S=4cdotpicdot R^2=4cdotpicdotBig(frac{D}{2}Big)^2=picdot D^2
S=π⋅D2S=picdot D^2
DD — диаметр шара.
Диаметр шара равен 10 (см.). Найдите площадь его поверхности.
Решение
D=10D=10
По формуле получаем:
S=π⋅D2=π⋅102≈314S=picdot D^2=picdot 10^2approx314 (см. кв.)
Ответ: 314 см. кв.
Студворк – лучший сайт для заказа контрольных работ!
Тест по теме «Площадь поверхности шара»
Геометрия, 11 класс
Урок №8. Сфера и шар
Перечень вопросов, рассматриваемых в теме:
- что такое сфера, какие у неё есть элементы (центр, радиус, диаметр сферы);
- что такое шар и его элементы;
- уравнение сферы;
- формула для нахождения площади поверхности сферы;
- взаимное расположение сферы и плоскости;
- теорема о радиусе сферы, который проведён в точку касания и теорему обратную данной.
Глоссарий по теме:
Определение
Окружность – множество точек плоскости, равноудалённых от данной точки. Данная точка называется центром окружности, расстояние от центра до любой точки окружности называется радиусом окружности.
Определение
Круг – это часть плоскости, ограниченная окружностью.
Определение
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Определение
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
Уравнение сферы

Определение
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Определение
Сегмент шара – это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Определение
Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 136-142.
Дополнительная литература:
Шарыгин И.Ф., Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений– М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-84.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”. https://mathb-ege.sdamgia.ru/test?theme=177
Теоретический материал для самостоятельного изучения
1. Основные теоретические факты
По аналогии с окружностью сферу рассматривают как множество всех точек равноудалённых от заданной точки, но только всех точек не плоскости, а пространства.
Рисунок 1 – Сфера с центром в точке О и радиусом R
Данная точка О называется центром сферы, а заданное расстояние – радиусом сферы (обозначается R). Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром (обозначается D). D=2R.
Определение
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки, которую называют центром.
Определение
Тело, ограниченное сферой, называется шаром.
Шар можно описать и иначе. Шаром радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек.
Сферу можно получить ещё одним способом – вращением полуокружности вокруг её диаметра, а шар – вращением полукруга вокруг его диаметра.
2. Уравнение сферы
Прежде чем вывести уравнение сферы введем понятие уравнения поверхности в пространстве. Для этого рассмотрим прямоугольную систему координат Oxyz и некоторую поверхность F. Уравнение с тремя переменными x, y, z называется уравнением поверхности F, если этому уравнению удовлетворяют координаты любой точки поверхности F и не удовлетворяют координаты никакой другой точки.
Пусть сфера имеет центром точку С (x0; y0; z0) и радиус R. Расстояние от любой точки М (x; y; z) до точки С вычисляется по формуле:
МС=
Исходя из понятия уравнения поверхности, следует, что если точка М лежит на данной сфере, то МС=R, или МС2=R2, то есть координаты точки М удовлетворяют уравнению:

Это выражение называют уравнением сферы радиуса R и центром С(x0; y0; z0).
3. Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости зависит от соотношения между радиусом сферы R и расстояния от центра сферы до плоскости d.
1. Пусть d
2. Пусть d=R. Если расстояние от центра сферы до плоскости равно радиусу сферы тогда сфера и плоскость имеют только одну общую точку, и в этом случае говорят, что плоскость касается сферы.
3. Пусть d
Рассмотрим случай касания более подробно.
Определение
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка – точкой касания.
Теорема (свойство касательной плоскости).
Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Теорема (признак касательной плоскости):
Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащей на сфере, то эта плоскость является касательной к сфере.
4. Основные формулы
Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

Формула для вычисления площади поверхности сферы и ее элементов:
S=4πR2 – площадь сферы.
S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

Примеры и разбор решения заданий тренировочного модуля
1. Площадь сечения шара, проходящего через его центр, равна 9 кв. м. Найдите площадь поверхности шара.
Решение:
Площадь круга вычисляется по формуле: Sкр=πR2.
Площадь поверхности шара вычисляется по формуле: Sсф=4πR2. Радиус шара и радиуса сечения, проходящего через центр шара, одинаковые. Поэтому площадь поверхности шара в 4 раза больше площади его диаметрального сечения. То есть площадь поверхности шара равна 36.
Ответ: 36
2. Вычислите радиус круга, площадь которого равна площади сферы радиуса 5.
Решение:
Площадь сферы равна Sсф=4πR2. То есть Sсф=100π.
По условию площадь круга некоторого радиуса r также равна 100π. Значит, r2 =100, то есть r=10.
Ответ: 10.
3. Все стороны треугольника АВС касаются сферы радиуса 5. Найти расстояние от центра сферы до плоскости треугольника, если АВ=13, ВС=14, СА=15
Решение:
Окружность, вписанная в треугольник, является сечением сферы.
Найдем ее радиус.
Площадь треугольника с известными сторонами можно вычислить по формуле Герона:

p=0,5(AB+BC+AC)=21

S=84.
С другой стороны, S=p·r.
Отсюда r=4.
Теперь найдем расстояние от центра шара до секущей плоскости.
Используем соотношение:



h=3.
Ответ: 3.
4. Вершины прямоугольника лежат на сфере радиуса 10. Найти расстояние от центра сферы до плоскости прямоугольника, если его диагональ равна 16.
Решение:
Так как вершины прямоугольника лежат на сфере, то окружность, описанная около прямоугольника, является сечением сферы.
Радиус окружности, описанной около прямоугольника, равен половине его диагонали, то есть r=8.
По условию задачи R=10.
Используем соотношение:



h=6.
Ответ: 6.
Напомним,
что шаром называется тело, состоящее из всех точек пространства,
находящихся на расстоянии не большем заданного от некоторой данной точки. Эта
точка – центр шара, а заданное расстояние – радиус шара.
Шар
так же, как цилиндр и конус, является телом вращения. Он получается в
результате вращения полукруга вокруг его диаметра.
Поверхность,
образуемая при этом вращении полуокружности, называется сферой. Можно
сказать, что сфера – это как бы оболочка, или граница, шара. Как окружность
есть граница круга, так и сфера – это граница шара.
Назовём
элементы сферы и шара.
Радиус
сферы – это отрезок, соединяющий центр сферы и любую её точку.
Хорда
сферы – отрезок, соединяющий две точки сферы.
Диаметр
сферы – хорда сферы, проходящая через её центр.
Радиус,
хорда, диаметр шара – это радиус, хорда, диаметр его сферы.
Любое
сечение шара плоскостью есть круг. Центром этого круга является основание
перпендикуляра, опущенного из центра шара на секущую плоскость.
Плоскость,
которая проходит через центр шара, называется диаметральной плоскостью.
Сечение ею шара – большим кругом, а сечение сферы – большой
окружностью.
Любая
диаметральная плоскость шара является его плоскостью симметрии. Центр
шара является его центром симметрии.
Плоскость,
проходящая через точку А сферы и перпендикулярно радиусу, проведённому в
эту точку, называется касательной плоскостью. Точка А называется точкой
касания.
Свойство
касательной плоскости к сфере: радиус сферы,
проведённый в точку касания, перпендикулярен касательной плоскости.
Признак
касательной плоскости к сфере: плоскость,
перпендикулярная радиусу сферы в конечной его точке на сфере, является
касательной к сфере.
Касательная
плоскость пересекается с шаром в единственной точке – в точке касания.
Касательной
прямой к сфере (шару) называется прямая, имеющая со сферой
единственную общую точку.
Отрезки
касательных к сфере, проведённые из одной точки, равны и составляют равные углы
с прямой, проходящей через эту точку и центр сферы.
Линией
пересечения двух сфер является окружность.
Площадь
сферы радиуса :
.
Объём
шара
радиуса :
.
Шаровым
сегментом называется часть шара, отсекаемая от него плоскостью.
Площадь боковой поверхности шарового сегмента:
.
Объём
шарового сегмента:
,
где
–
радиус шара, –
высота шарового сегмента.
Шаровым
сектором называется тело, которое получается из шарового
сегмента и конуса, основанием которого является сечение плоскостью данного шара.
Площадь
боковой поверхности шарового сектора:
.
Объём
шарового сектора:
,
где
–
радиус шара, –
высота сегмента.
Шар
называется вписанным в многогранник, а многогранник – описанным около
шара, если поверхность шара касается всех граней многогранника.
Шар
называется описанным около многогранника, а многогранник – вписанным
в шар, если поверхность шара проходит через все вершины многогранника.
Шар
называется вписанным в цилиндр, а цилиндр – описанным около шара,
если поверхность шара касается оснований цилиндра и всех образующих.
Шар
называется описанным около цилиндра, если окружности оснований цилиндра
принадлежат поверхности шара.
Шар
называется вписанным в конус (усечённый конус), а конус
(усечённый конус) – описанным около шара, если поверхность шара касается
основания (оснований) конуса и всех образующих.
Шар
называется описанным около конуса (усечённого конуса), если окружность
основания и вершина (окружности оснований) конуса принадлежат поверхности шара.
Если
боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую
пирамиду можно вписать шар.
Около
пирамиды можно описать шар тогда и только тогда, когда около её основания можно
описать окружность.
Если
боковые рёбра пирамиды равны между собой (или одинаково наклонены к плоскости
основания), то около такой пирамиды можно описать шар.
В
призму можно вписать шар тогда и только тогда, когда в перпендикулярное
сечение этой призмы можно вписать окружность, а высота призмы равна диаметру
окружности, вписанной в это перпендикулярное сечение.
Описать
шар около призмы можно тогда и только тогда, когда призма прямая и около её основания
можно описать окружность.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. Радиус шара увеличили в раза.
Во сколько раз увеличился объём шара?
Решение.
Задача
вторая. Объём шара равен см3.
Найдите диаметр шара.
Решение.
Задача
третья. Шар пересечен плоскостью. Площадь сечения равна см2.
Расстояние от центра шара до плоскости сечения равно см.
Найдите площадь поверхности шара.
Решение.
Задача
четвёртая. В конус с радиусом основания, равным см,
и высотой, равной см,
вписан шар. Найдите отношение площади боковой поверхности конуса к площади
поверхности шара.
Решение.
Задача
пятая. Найдите объём шарового сектора, если радиус
окружности его основания равен см,
а радиус шара – см.
Решение.
Задача
шестая. Шар с радиусом см
пересечён плоскостью, находящейся на расстоянии см
от центра шара. Найдите площадь сечения.
Решение.
Преподаватель который помогает студентам и школьникам в учёбе.
Шаровая поверхность в начертательной геометрии с примером
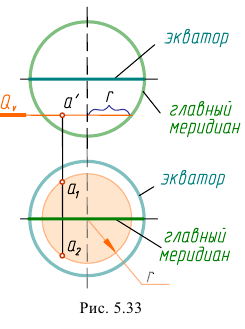
Шаровая поверхность:
Шаровой поверхностью (или сферой) называется поверхность, образованная при вращении окружности вокруг своего диаметра.
Если шаровая поверхность пересекается плоскостью, то в сечении всегда получается окружность. Эта окружность может спроецироваться:
- – в прямую, если секущая плоскость перпендикулярна плоскости проекций;
- – в окружность, если секущая плоскость параллельна плоскости проекций. Например, окружность с радиусом
- – в эллипс, если секущая плоскость не параллельна плоскости проекций.
Чтобы построить проекции точки, лежащей на поверхности шара, необходимо через нее провести секущую плоскость, параллельную плоскости проекций, затем построить окружность, на которой находится эта точка.
Пересечение шаровой поверхности плоскостью
Пересечем поверхность шара фронтально-проецирующей плоскостью 
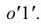
Развертка поверхности шара
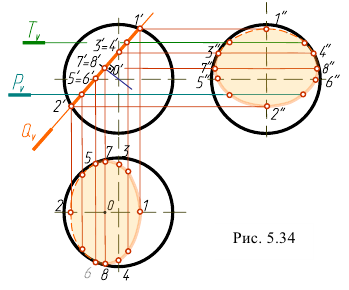
Сферическая поверхность относится к неразвертываемым поверхностям, и поэтому развертка поверхности шара может быть выполнена только приближенными способами. Рассмотрим один из способов выполнения развертки шара.
Для выполнения развертки поверхности шара поверхность делят меридианами на равные части. На рис. 5.35, а шар разделен на 12 равных частей. Представим себе, что все 12 частей поверхности шара отогнуты от полюсов и поставлены в вертикальное положение. Сферическая поверхность условно развернется как цилиндрическая поверхность, состоящая из 12 вертикально расположенных секций. Если эти секции разместить в одной плоскости, то получится приближенная развертка поверхности шара, рис. 5.35, б. Для построения 12 меридианов очерковые окружности шара на горизонтальной и фронтальной проекциях делят на 12 равных частей.
На горизонтальной проекции меридианы спроецируются в отрезки, проходящие через центр проекции шара. Фронтальные проекции этих меридианов будут кривыми, и их строят с помощью параллелей, проведенных через точки деления фронтального меридиана.
Для построения развертки достаточно знать размеры одной секции. На рис. 5.35, а выделена одна такая секция, на проекциях которой отмечены точки пересечения двух меридианов, являющихся ее сторонами, с параллелями. Так как экватор делит секцию на две одинаковые части (верхнюю и нижнюю). То точки взяты только на той части секции, которая расположена выше экватора.
Самый широкий участок секции расположен по экватору. Его ширина равна 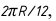
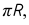
При развертке поверхности шара экватор развернется в отрезок, длина которого будет равна 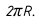
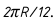
Через середину построенных отрезков проводят оси симметрий перпендикулярно экватору. Затем вверх и вниз от экватора откладывают длину развернутых участков меридианов, заключенных между параллелями. Их длина равна 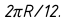
- Винтовые поверхности
- Способ вспомогательных секущих плоскостей
- Способ вспомогательных сфер
- Выполнение и оформление чертежей по ГОСТ и ЕСКД
- Построение проекций линии пересечения цилиндра плоскостью
- Развертка поверхности цилиндра
- Построение проекций линий пересечения конуса плоскостью
- Развертка поверхности конуса