Как найти плоскость в пучке плоскостей

Пучком плоскостей
называют совокупность всех плоскостей,
имеющих общуюлинию пересечения (ось пучка).

Пусть имеем
плоскости
:и:.
Определим их линию пересечения заданием
системы уравнений:

(9)

Имея
линию пересечения (9), можно было бы
выделять в пространстве плоскости,
содержащие эту линию (прямую) и заданную
точку
.
Оказывается,
гораздо удобнее задать пучок плоскостей
в виде равенства:

:
+=0, (10)

или в форме: :+++=0,
(11)

причем конкретные
значения параметров
и(их отношение!) определяют по дополнительной
информации, выделяющей из пучка заданную
плоскость. Так как по условию плоскости
пересекаются, то коэффициенты при
переменныхне могут одновременно обратиться в
нуль, и для любых пар значенийи(10) или (11) определяет некоторую плоскость!

Из (10) видим, что
при q=0 из пучка
выделяется плоскость,
а при=0
плоскость.
Если в (10) подставить координаты точки
линии пересечения, то обе скобки равенства
обращаются в нуль (система(9)).
Это значит плоскость (10) содержит линию
пересечения.

☺☺

Пример 4–20:
Составить уравнение плоскости ,
проходящей через точку
(2,3,1)
и прямую ,
определяемую плоскостями :
и :.

Решение:

0).
Если решать задачу с привлечением
минимальных средств, то схема решения
могла быть такой: найти линию пересечения
заданных плоскостей

и
,
провести плоскость через точку и любые
две точки линии пересечения.

1). Мы воспользуемся
свойством пучка содержать линию
пересечения неявно. Для этого достаточно
записать:

:
+=0,

где
и– произвольные числа.

2).
Определим значения параметров
и
из условия :

·(2+3–2·1+1)+·(2·2–3+1–4)=0
→.

3). Приняв
=1
и=2,
получим: 1·+
2·=0,
выделяем из пучка искомую плоскость:,
содержащую точку.

Ответ: уравнение
:.

Пример 4–21:
Составить уравнение плоскости ,
проходящей через прямую, определяемую
плоскостями :
и :,
и параллельной плоскости
:
.

Решение:

1).
Обозначим вектор нормали произвольной
плоскости пучка как
,
а искомой плоскости как вектор
==(5,–1,0).

2).
Составим уравнение пучка плоскостей в
виде:

:
+=0,

или

:
=0.

3). Так
как из пучка плоскостей выделяется одна
из плоскостей, то примем: =.
Из равенства векторов получаем:
=(5,–1,0),
откуда имеем k=2.

4). После чего легко
получаем уравнение искомой плоскости:
.

Ответ: уравнение
:.

Пример 4–22:
Составить уравнение плоскости ,
принадлежащей пучку плоскостей :

и :

и равноудалённой от точек (3,–4,–6)
и (1,2,2).

Р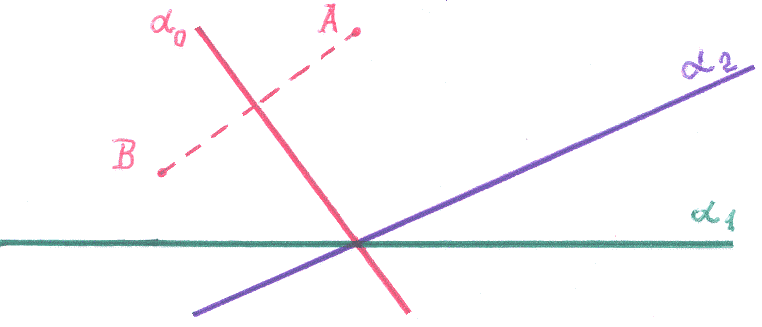ешение:

0). Если
решать задачу с привлечением минимальных
средств, то схема решения могла быть
такой: найти линию пересечения заданных
плоскостей

и
,
найти среднюю точку отрезка
(обозначим её
)
и провести плоскость через точку

и любые две точки линии пересечения.

1).
Составим уравнение пучка плоскостей в
виде:

: 1·+=0,
или:

: =0.

Замечание:
Учитывая, что расстояния можно сравнивать,
применяя один и тот же отрезок в качестве
меры длины, не обязательно единичный
(!), мы не станем «нормировать» уравнение
плоскости.=.

Так как
решение одной и той же задачи разными
способами особенно полезно в освоении
любой области знаний, применим два
вполне рациональных, использующих уже
рассмотренные примеры, способа.

Способ-1:
выделение плоскости
из пучка при помощи точки
.

2).
Вычислим координаты точки

из условия: 2=+=(4,–2,–4),
откуда
=(2,–1,–2).

3).
Определим значение параметра
из условия :

=0,
откуда
=–2.

4). Уравнение искомой
плоскости
:.

Способ-2:
выделение плоскости
из пучка при помощи свойства равной
удалённости от заданных точек
,.

5). Так
как точки

и

располагаются по разные стороны плоскости

=,
то величины

и

имеют разные знаки. Но мы сравниваем
расстояния, и потому необходимо это
отразить в виде условия:
=–,
или +=0.
Учитывая координаты точек

и ,
получаем:

(3+2k)·3–(4+3k)·(–4)+(1+k)·(–6)+(6+2k)+(3+2k)·1–(4+3k)·2+(1+k)·2+(6+2k)=0,
откуда =–2.

3). Уравнение искомой
плоскости
:.

Замечание:
сравнение способов показывает значительный
выигрыш по трудоёмкости у способа-1,
также в этом способе удаётся обойтись
меньшим количеством средств.

Ответ: уравнение
:.

☻

Соседние файлы в папке ЛА и АГ пособие

• #
• #
• #
• #
• #
• #
• #

Не вижу связи между неверным равенством 2+0=0 и последующими словами “итак, получили”. Для того чтобы проверить принадлежность точки плоскости надо было сначала придти к ложному равенству? Ну и как же эта плоскость (которая “и есть”) входит в Ваш недопучок? При какой лямбде она получается?

Цитата:

Ну, хорошо, мы ошиблись, пример уравнением пучка прямых с двумя произвольными параметрами можно решить методом подбора корней, но при этом избыточность одного какого-либо произвольного параметра остаётся.

Да не подбором, а однозначным решением (если только не вздумаем проводить через точку на пересечении плоскостей) с точностью до ненулевого множителя. Для уравнения такой множитель – тьфу и сократить, зато ни одна плоскость как у Вас из пучка не ускользнёт.

Положение здесь ровно такое же как с уравнением прямых на плоскости. Если их рассматривать только в виде [math]y=kx+b[/math], то из рассмотрения исчезают вертикальные прямые [math]x=text{const}[/math]. А вот общее уравнение [math]ay+by+c=0[/math] описывает все.

982 Составить уравнения прямых,
образованных пересечением плоскости с
координатными плоскостями. 983 Составить
уравнения прямой, образованных пересечением
плоскости с плоскостью, проходящей
через ось Ох и точку Е(3; 2; -5). 984 Найти точки
пересечения прямой с координатными
плоскостями. 985 Доказать, что
прямая пересекает ось Оу. 986 Определить, при
каком значении D прямая пересекает: 986.1 ось Ох; 986.2 ось Оу; 986.3 ось Oz. 987 Найти соотношения,
которым должны удовлетворять коэффициенты
уравнений прямой 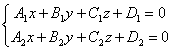для того, чтобы эта
прямая была параллельна: 987.1 оси Ох; 987.2 оси Оу; 987.3 оси Oz. 988 Найти соотношения,
которым должны удовлетворять коэффициенты
уравнений прямой 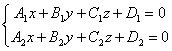для того, чтобы эта
прямая: 988.1 пересекала ось
абсцисс; 988.2 пересекала ось
ординат; 988.3 пересекала ось
апликат; 988.4 совпадала с осью
абсцисс; 988.5 совпадала с осью
ординат; 988.6 совпадала с осью
апликат. 989 В пучке плоскостей найти плоскость, которая: 989.1 проходит через
точку М₁(1; -2; 3); 989.2 параллельна оси Ох; 989.3 параллельна оси Оу; 989.4 параллельна оси Oz. 990 Составить
уравнение плоскости, которая проходит через
прямую пересечения плоскостей , : 990.1 и через точку М₁(4; -2; -3); 990.2 параллельно оси Ох; 990.3 параллельно оси Оу; 990.4 параллельно оси Oz. 991 Составить
уравнение плоскости, проходящей через прямую
пересечения плоскостей , параллельно
вектору l={2; -1; -2}. 992 Составить
уравнение плоскости, проходящей через прямую
пересечения плоскостей , параллельно
вектору l={7; 9; 17}. 993 Составить
уравнение плоскости, проходящей через прямую
пересечения плоскостей , перпендикулярно
плоскости . 994 Составить
уравнение плоскости, проходящей через прямую перпендикулярно плоскости . 995 Составить
уравнение плоскости, которая проходит через
прямую пересечения плоскостей , параллельно
отрезку, ограниченному точками М₁(2; 5; -3),
М₂(3; -2; 2). 996 Написать уравнение
плоскости, принадлежащей пучку плоскостей и равноудаленной от точек М₁(3;
-4; -6) и М₂(1; 2; 2). 997 Определить,
принадлежит ли плоскость пучку
плоскостей . 998 Определить,
принадлежит ли плоскость пучку
плоскостей . 999 Определить, при
каких значениях l и m плоскость принадлежит
пучку плоскостей . 1000 Написать уравнение
плоскости, которая принадлежит пучку плоскостей и отстоит от начала координат на
расстояние d=3. 1001 Написать уравнение
плоскости, которая принадлежит пучку плоскостей и отстоит от точки
С(3; -2; -3) на расстояние d=7. 1002 Найти уравнение
плоскости, которая принадлежит пучку плоскостей и отсекает от координатного угла Оху
треугольник с площадью, равной 6. 1003 Составить
уравнения плоскостей, проектирующих прямую на координатные плоскости. 1004 Составить
уравнения проекций прямой на
координатные плоскости. 1005 Составить
уравнение плоскости, проектирующей прямую на плоскость . 1006 Составить
уравнения проекции прямой на
плоскость .

Совокупность всех плоскостей, проходящих через заданную прямую L, называется пучком плоскостей, а прямая -осью пучка.

Пусть ось пучка задана уравнениями

Почленно умножим второе уравнение системы (35) на постоянную и сложим с первым уравнением:

Уравнение – первой степени относительно и, следовательно, при любом численном значении К определяет некоторую плоскость. Так как уравнение (36) есть следствие уравнений (35), то координаты точки, удовлетворяющие уравнениям (35), будут удовлетворять и уравнению (36). Следовательно, при любом численном значении X уравнение (36) есть уравнение плоскости, проходящей через прямую (35).

Покажем, что всякая плоскость пучка плоскостей с осью, заданной уравнениями (35), кроме плоскости может быть представлена в виде (36). Действительно, любая плоскость пучка определяется ее точкой не лежащей на оси пучка.

Чтобы найти уравнение этой плоскости, подставим в уравнение (36) координаты точки

(37)

Из уравнения (37) найдем значение если , т. е. если точка не лежит во второй из данных плоскостей (35). Подставляя найденное значение в уравнение (36), получим уравнение плоскости пучка, проходящей через точку

Итак, уравнение (36) при различных значениях дает уравнение любой плоскости пучка, ось которого задана уравнениями (35), кроме плоскости

Поэтому уравнение (36) называется уравнением пучка плоскостей. Уравнение пучка плоскостей используют при решении задач, в которых требуется найти плоскость, проходящую через заданную прямую, причем значение множителя X обычно находят из какого-либо дополнительного условия, которое определяет положение искомой плоскости.

Рассмотрим примеры.

Пример 1. Найти уравнение плоскости, проходящей через прямую

и точку .

Решение. Запишем уравнение пучка плоскостей, проходящих через данную прямую:

Подставим в уравнение пучка координаты точки

Следовательно, Подставляя найденное значение в уравнение пучка, найдем уравнение искомой плоскости:

Пример 2. Найти уравнение плоскости, проходящей через прямую перпендикулярно плоскости

Решение. Представляем данную прямую как пересечение ее проектирующих плоскостей:

Составляем уравнение пучка плоскостей:

или

Записываем условие перпендикулярности плоскости и данной плоскости

Решая это уравнение, находим . Подставляя найденное значение К в уравнение пучка получим

или

Решение типовых задач по теме “Задание плоскости в пространстве”. Часть 4
Задача №1. Составить уравнение плоскости, проходящей через линию пересечения плоскостей Зx+y+z-4=0, x+3z-5=0 и отсекающей на осях Ох и Оу равные от­резки.
Решение. Уравнение пучка плоскостей, проходя­щих через линию пересечения двух данных плоскостей, имеет вид:

или

Запишем это уравнение в виде уравнения в отрезках:

или

Согласно условию, отрезки, отсекаемые на осях Ох и 0y, равны, т. е.

Таким образом, искомым уравнением плоскости яв­ляется уравнение:

Ответ: х+у-5z+6=0.
Задача №2. Из пучка, определяемого плоскостями Зх+у-2z-6=0 и х-2y+5z-1=0 выделить две взаимно перпендикулярные плоскости, из которых одна проходит через точку А(2;-3;4).
Решения задач №1 и №2 подробно изложены в следующем видео

Задача №5. Установить, что три плоскости 2x-4y+5z-21=0, х-3z+18=0, 6х+y+z-30=0 имеют общую точку, и вычислить ее координаты.
Решение. Если определитель системы

отличен от нуля, то три плоскости, выражаемые данны­ми уравнениями, пересекаются в единственной точке:

Плоскости имеют общую точку. Найдем ее:

Ответ: M(3;5;7).
Задача №6. Проверить, имеют ли общую точку следующие четыре плоскости:
а) 2х+2у-3z-9=0, 5х-у+8z-1=0, x+3y+2z-1=0 и Зx+5у-z-10=0;
б) 2х-4y-z+5=0, Зx+5у+4z-3=0, 2у+3z—1=0 и 5x+2y-2=0.
Решения задач №5 и №6 подробно изложены в следующем видео