Поверхностная плотность заряда
Напряженность электрического поля зависит от величины заряда и конфигурации заряженного тела.
Поверхностная плотность заряда — есть отношение заряда к площади заряженной поверхности.
Единица СИ поверхностной плотности заряда:
[ [σ] = frac{кулон}{квадратный enspace метр} = frac{Кл}{м^2} ]
Если
| σ | поверхностная плотность заряда, | Кулон/метр2 |
|---|---|---|
| Q | заряд поверхности проводника, | Кулон |
| S | площадь поверхности проводника, | метр2 |
то
[ σ = frac{Q}{S} ]
Вычислить, найти поверхностную плотность заряда по формуле (2)
Наличие зарядов приводит к возникновению сил, которые в свою очередь действуют на заряды, помещенные в электрическое поле. Причина и следствие здесь взаимно переплетаются.
Если
| σ | поверхностная плотность заряда, | Кулон/метр2 |
|---|---|---|
| E | напряженность электрического поля, | Вольт/метр |
| ε0 | электрическая постоянная, 8.85·10-12 | Кулон/(Вольт · метр) |
то
[ σ = ε_0 · E ]
Вычислить, найти поверхностную плотность заряда через напряженность электрического поля по формуле (3)
Поверхностная плотность заряда |
стр. 626 |
|---|
Как найти плотность через напряжение

Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах.
Поле бесконечной однородно заряженной плоскости
Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:

где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности.
Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность  во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).
Очевидно, что в симметричных, относительно плоскости точках, напряженность  будетодинакова по величине и противоположна по направлению.
будетодинакова по величине и противоположна по направлению.
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).
 |
|
| Рис. 2.11 | Рис. 2.12 |
Применим теорему Остроградского-Гаусса. Поток ФЕ через боковую часть поверхности цилиндра равен нулю, т.к .  Дляоснования цилиндра
Дляоснования цилиндра 
Суммарный поток через замкнутую поверхность (цилиндр) будет равен:

Внутри поверхности заключен заряд  . Следовательно, из теоремы Остроградского–Гаусса получим:
. Следовательно, из теоремы Остроградского–Гаусса получим:
откуда видно, что напряженность поля плоскости S равна:
Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости 
Поле двух равномерно заряженных плоскостей
Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.13).
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей  .
.
Вне плоскостей напряженность поля 


Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).
Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):
Механические силы, действующие между заряженными телами, называют пондермоторными.
Тогда сила притяжения между пластинами конденсатора:
где S – площадь обкладок конденсатора. Т.к.  , то
, то
Это формула для расчета пондермоторной силы.
Поле заряженного бесконечно длинного цилиндра (нити)
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью  , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).
, где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).

Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров  для боковой поверхности
для боковой поверхности  т.е. зависит от расстояния r.
т.е. зависит от расстояния r.
Следовательно, поток вектора  через рассматриваемую поверхность, равен
через рассматриваемую поверхность, равен 
При  на поверхности будет заряд
на поверхности будет заряд  По теореме Остроградского-Гаусса
По теореме Остроградского-Гаусса  , отсюда
, отсюда
Если 
 , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).
, т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).

Если уменьшать радиус цилиндра R (при  ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при
), то можно вблизи поверхности получить поле с очень большой напряженностью и, при  , получить нить.
, получить нить.
Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком
Внутри меньшего и вне большего цилиндров поле будет отсутствовать  (рис. 2.16) .
(рис. 2.16) .

В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае:

Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).
Поле заряженного пустотелого шара
Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным,  – в любой точке проходит через центр шара.
– в любой точке проходит через центр шара.  ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).
Если  то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
Внутри сферы, при  поле будет равно нулю, т.к. там нет зарядов:
поле будет равно нулю, т.к. там нет зарядов: 


Как видно из (2.5.7) вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.
Поле объемного заряженного шара
Для поля вне шара радиусом R (рис. 2.18) получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула:
Но внутри шара при  сферическая поверхность будет содержать в себе заряд, равный
сферическая поверхность будет содержать в себе заряд, равный

где ρ – объемная плотность заряда, равная:  ;
;  – объем шара. Тогда по теореме Остроградского-Гаусса запишем:
– объем шара. Тогда по теореме Остроградского-Гаусса запишем:
Таким образом, внутри шара 
Источник

Электрическим током называют направленное движение свободно заряженных частиц под действием электрического поля.
Как правило движение зарядов происходит в некоторой среде (веществе или вакууме), являющейся проводником для электрического тока. Движущимися в среде заряженными частицами могут быть электроны (в металлах, полупроводниках) или ионы (в жидкостях и газах).

Для возникновения и протекания электрического тока в любой токопроводящей среде необходимо выполнение двух условий:
- Наличие в среде свободных носителей заряда;
- Наличие электрического поля.
Для поддержания электрического поля, например в проводнике, к его концам необходимо подключить какой-либо источник электрической энергии (батарейку или аккумулятор). Поле в проводнике создается зарядами, которые накопились на электродах источника тока под действием сил (химических, механических и т.д.).
За направление тока условно принято принимать направление движения положительных зарядов. Следовательно, условно принятое направление тока обратно направлению движения электронов – основных отрицательных электрических носителей заряда в металлах и полупроводниках.
Понять явление электрического тока достаточно сложно так как его невозможно увидеть глазами. Для лучшего понимания процессов в электронике проведем аналогию между электрическим током в проводнике и водой в тонкой трубочке. В трубочке есть вода (носители заряда в проводнике), но она неподвижна, если трубочка лежит на горизонтальной поверхности и уровень высот ее концов (значения потенциалов электрического поля) одинаковый. Если трубочку наклонить так, что один конец станет выше другого (появится разность потенциалов), вода потечет по трубочке (электроны придут в движение).
Способность вещества проводить электрический ток под действием электрического поля называется электропроводностью. Каждому веществу соответствует определенная степень электропроводности. Ее значение зависит от концентрации в веществе носителей заряда – чем она выше, тем больше электропроводность. В зависимости от электропроводности все вещества делятся на три большие группы: проводники, полупроводники и диэлектрики.
Электрический ток может менять направление и величину во времени (переменный ток) или оставаться неизменным (постоянный) (рисунок 2).

Количественной мерой электрического тока служит сила тока I, которая определяется числом электронов (зарядов) q, проходящих через импровизированное поперечное сечение проводника в единицу времени t (рисунок 3).


Для постоянного тока представленное выше выражение можно записать в виде

Ток в системе СИ измеряется в амперах, [А]. Току в 1 А соответствует ток, при котором через поперечное сечение за 1 секунду проходит электрический заряд, равный 1 Кл.
1 A = 1 Кл/1 сек.
Плотность электрического тока
Под плотностью тока j понимается физическая величина, равная отношению тока I к площади поперечного сечения S проводника. При равномерном распределении тока по поперечному сечению проводника.
J = I/S
Плотность тока в системе СИ измеряется в амперах на миллиметр квадратный, [А/мм2].
Рассмотрим плотность тока в проводнике с разным поперечным сечением. Например, соединены два проводника с различными сечениями: первый толстый провод с большим поперечным сечением S1 второй тонкий провод с сечением S2. К концам которых приложено постоянное напряжение (рисунок 5) в следствии чего через них протекает постоянный ток с одинаковой силой тока.
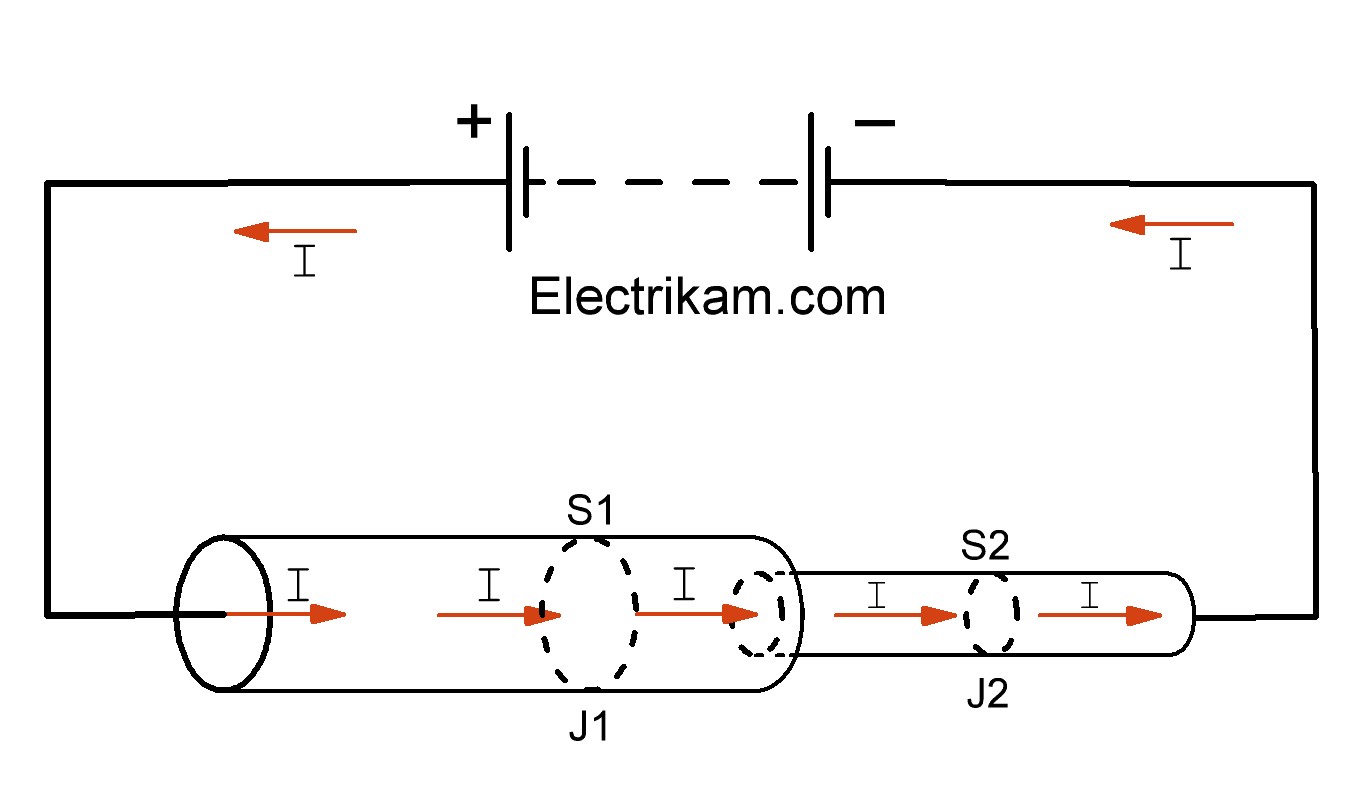
Предположим, что сила тока через поперечное сечение толстого проводника S1 и тонкого провода S2 различная. Из этого предположения вытекает, что за каждую единицу времени через сечения S1 и S2 протекают различные значения электрического заряда. Следовательно, в объёме провода, расположенного между двумя указанными сечениям происходит непрерывное скапливание зарядов, и напряженность электрического поля изменялась бы, чего не может быть, так как при изменении электрического поля ток был бы непостоянен. В проводах с различным сечением при одном и том же токе плотность тока обратно пропорциональна площади поперечного сечения.
I = J1S1 = J2S2
Плотность тока — векторная величина.


Направление вектора ![]() совпадает с направлением положительно заряженных зарядов и, следовательно, с направлением самого тока I.
совпадает с направлением положительно заряженных зарядов и, следовательно, с направлением самого тока I.
Если концентрация носителей тока равна n, каждый носитель имеет заряд e и скорость его движения в проводнике равна v (рисунок 3), то за время dt через поперечное сечение S проводника переносится заряд
![]()
В этом случае величину силы тока I можно представить в виде зависимости

а плотность тока
![]()
Сила тока через произвольную поверхность определяется через поток вектора плотности тока, как интеграл по произвольной (в общем случае) поверхности S (рисунок 6)


От величины плотности тока зависит важный показатель – качество электропередачи. Фактически этот показатель зависит от степени нагрузки проводника (хотя и не только от нее). В зависимости от значения плотности тока принято выбирать сечение проводов – это связано с наличием у проводников сопротивления, в результате которого происходит нагрев жил проводника вплоть до его расплавления и выхода из строя.
#1. … – направленное движение свободно заряженных частиц под действием электрического поля.
Электрический заряд
Электрический ток
Электропроводность
#2. Как направлен ток в металлическом проводе?
обратно движению основных носителей заряда
со направлено движению основных носителей заряда
перпендикулярно движению заряда

#3. В каком проводнике плотность тока выше?
В толстом
Одинакова
В тонком
Плотность тока для каждого проводника:
J1 = I/S1 J2 = I/S2
Так как сила тока в проводах одинакова:
J1 < J2
Результат
Отлично!
Попытайтесь снова(
Условие задачи:
Найти плотность тока в стальном проводнике длиной 10 м, на который подано напряжение 0,12 В.
Задача №7.1.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(L=10) м, (U=0,12) В, (j-?)
Решение задачи:
Плотность тока (j) по определению равна отношению силы тока (I) на площадь поперечного сечения проводника (S), то есть:
[j = frac{I}{S};;;;(1)]
Согласно закону Ома для участка цепи сила тока (I) прямо пропорциональна напряжению на участке (U) и обратно пропорциональна сопротивлению этого участка (R), поэтому:
[I = frac{U}{R};;;;(2)]
Сопротивление стальной проволоки (R) легко определить по такой известной формуле (здесь (rho) – удельное электрическое сопротивление стали, равное 120 нОм·м):
[R = rho frac{L}{S};;;;(3)]
Сначала подставим (3) в (2), тогда:
[I = frac{{US}}{{rho L}}]
Полученное выражение подставим в (1):
[j = frac{{US}}{{rho LS}}]
[j = frac{U}{{rho L}}]
Задача решена в общем виде, теперь необходимо лишь подставить данные задачи в полученную формулу и посчитать ответ:
[j = frac{{0,12}}{{120 cdot {{10}^{ – 9}} cdot 10}} = {10^5};А/м^2 = 0,1;А/мм^2]
Ответ: 0,1 А/мм2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.1.8 Определить плотность тока, если за 0,4 с через проводник сечением 1,2 мм2 прошло
7.1.10 Какое напряжение надо приложить к концам стального проводника длиной 30 см
7.1.11 Допустимый ток для изолированного медного провода площадью поперечного сечения
Сосредоточенные и распределенные заряды
Заряды можно распределять по какой-либо области тел, тогда их называют распределенными. Когда же заряд целиком собран в одну точку, его называют точечным. Большинство школьных задач физики связано с точечными зарядами.
Сосредоточенный заряд
Электрический заряд, сосредоточенный в какой-либо точке пространства, называют точечным.

Рис. 1. Точечный заряд
Силу взаимодействия точечных зарядов можно вычислить, используя закон Кулона.
Распределенные заряды
Электрический заряд, так же, можно распределять по объему, площади, или длине. Такие заряды называют распределенными. Чтобы описать эти заряды, используют понятие плотности заряда.
Если заряд распределен по:
— объему, говорят о объемной плотности заряда;
— площади, употребляют поверхностную плотность;
— длине, используют линейную плотность.
Примечание: Плотности отрицательных зарядов записывают со знаком «минус».
Формула линейной плотности заряда

Рис. 2. Заряд распределен по длинному тонкому телу
[ large boxed {tau = frac{q}{L} } ]
( large q left(text{Кл} right) ) – заряд;
( large L left(text{м} right) ) – длина, по которой распределен заряд;
( large tau left(frac{text{Кл}}{text{м}} right) ) – линейная плотность заряда;
Формула поверхностной плотности заряда
Любая поверхность обладает площадью, распределяя по ней заряд, получим поверхностную его плотность.
Этот термин используют, например, для вычисления электрического поля заряженной плоскости, или плоского конденсатора (двух параллельных плоскостей).

Рис. 3. Заряд распределен по плоской поверхности
[ large boxed {sigma = frac{q}{S} } ]
( large S left(text{м}^{2} right) ) – площадь, по которой распределен заряд;
( large sigma left(frac{text{Кл}}{text{м}^{2}} right) ) – поверхностная плотность заряда;
Формула объемной плотности заряда
Функция, описывающая плотность распределения заряда в трехмерном пространстве, входит в одно из уравнений Максвелла.

Рис. 4. Заряд распределен по объему тела
[ large boxed {rho = frac{q}{V} } ]
( large V left(text{м}^{3} right) ) – объем, по которому распределен заряд;
( large rho left(frac{text{Кл}}{text{м}^{3}} right) ) – объемная плотность заряда;
Примечание:
Джеймс Клерк Максвелл (1831 — 1879) – талантливый шотландский математик и физик. Популяризатор науки, экспериментатор и конструктор научных приборов.
Описал электромагнитное взаимодействие с помощью своих уравнений (уравнения Максвелла). Система этих уравнений лежит в основе современной электродинамики.
Предсказал электромагнитные волны, обнаружил, что свет имеет электромагнитную природу и может создавать давление.
Занимался исследованиями в области молекулярной физики и термодинамики. Использовал математический аппарат статистики, получил температурное распределение скоростей молекул.
Проводил исследования в области астрономии и оптики, для планеты Сатурн провел анализ устойчивости колец.
Именно Максвелл заложил трехцветный принцип, который используется в цветной фотографии и телевидении.
Оценка статьи:
![]() Загрузка…
Загрузка…
