Выясним, как будет выглядеть соотношение (5.1), если в него ввести молярную газовую постоянную  Так как
Так как  — полное число молекул в массе газа
— полное число молекул в массе газа  — число молекул в одном моле, то
— число молекул в одном моле, то

где  — число молен в массе газа
— число молен в массе газа  Поэтому
Поэтому

Поскольку  равно массе газа
равно массе газа  деленной на массу одного моля газа
деленной на массу одного моля газа  то получаем
то получаем

Соотношение (5.7) называется уравнением Клапейрона — Менделеева или уравнением состояния для произвольной массы идеального газа. Для одного моля идеального газа уравнение Клапейрона — Менделеева принимает вид

С помощью формулы (5.7) легко выяснить, какими величинами определяется плотность газа. Так как  то из (5.7) имеем
то из (5.7) имеем

Уравнение состояния идеального газа
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:
Уравнение состояния идеального газа
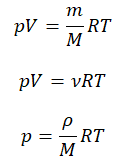
Внимание! При решении задач важно все единицы измерения переводить в СИ.
Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.
Из основного уравнения состояния идеального газа выразим массу:
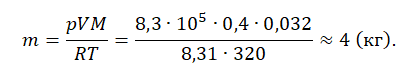
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.
Подсказки к задачам
Важна только та масса, что осталась в сосуде. Поэтому:
| Давление возросло на 15% | p2 = 1,15p1 |
| Объем увеличился на 2% | V2 = 1,02V1 |
| Масса увеличилась в 3 раза | m2 = 3m1 |
| Газ нагрелся до 25 о С | T2 = 25 + 273 = 298 (К) |
| Температура уменьшилась на 15 К (15 о С) | T2 = T1 – 15 |
| Температура уменьшилась в 2 раза | 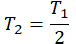 |
| Масса уменьшилась на 20% | m2 = 0,8m1 |
| Выпущено 0,7 начальной массы | |
| Какую массу следует удалить из баллона? | Нужно найти разность начальной и конечной массы: |
| Газ потерял половину молекул | 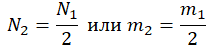 |
| Молекулы двухатомного газа (например, водорода), диссоциируют на атомы | 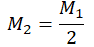 |
| Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ) | M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль |
| Открытый сосуд | Объем V и атмосферное давление pатм остаются постоянными |
| Закрытый сосуд | Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины |
| Нормальные условия | Температура T0 = 273 К Давление p0 = 10 5 Па |
| Единицы измерения давления | 1 атм = 10 5 Па |
Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.
2,8 МПа = 2,8∙10 6 Па
1,5 МПа = 1,5∙10 6 Па
Так как половина молекул была выпущена, m2 = 0,5m1. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:
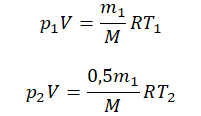
Преобразим уравнения и получим:
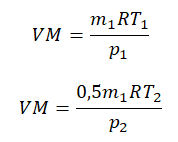
Приравняем правые части и выразим искомую величину:
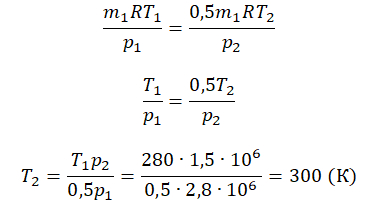
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
Алгоритм решения
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.
Уравнение состояния идеального газа. Газовые законы.
Уравнение состояния идеального газа
(уравнение Менделеева – Клапейрона).
Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние.
В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеального газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул.
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.
Мы знаем, что 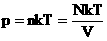 . Следовательно,
. Следовательно, 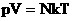 . Учитывая, что
. Учитывая, что 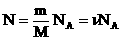 , получим:
, получим: 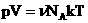 .
.
Произведение постоянных величин есть величина постоянная, следовательно: 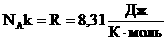 — универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).
— универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).
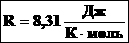
Таким образом, имеем:
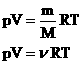 — уравнение состояния (уравнение Менделеева – Клапейрона).
— уравнение состояния (уравнение Менделеева – Клапейрона).

Другие формы записи уравнения состояния идеального газа.
1.Уравнение для 1 моля вещества.
Если n=1 моль, то, обозначив объем одного моля Vм, получим: 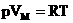 .
.
Для нормальных условий получим: 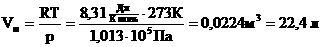

2. Запись уравнения через плотность: 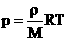 — плотность зависит от температуры и давления!
— плотность зависит от температуры и давления!
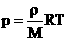
3. Уравнение Клапейрона.
Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда: 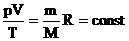
Эта запись означает, что для данной массы данного газа справедливо равенство: 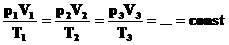
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: 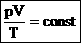 .
.
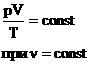
Газовые законы.
1. Закон Авогадро.
В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов).
Доказательство: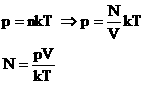
Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.
2. Закон Дальтона.
Давление смеси газов равно сумме парциальных (частных) давлений каждого газа.
Доказательство: 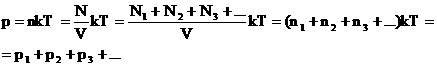
3. Закон Паскаля.
Давление, производимое на жидкость или газ, передается во все стороны без изменения.
Уравнение Клапейрона-Менделеева
Что такое уравнение Клапейрона-Менделеева
Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.
Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.
Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.
Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.
Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:
p V = c o n s t * T
В представленном выше уравнении состоянии газа под const подразумевается количество молей.
Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.
p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.
Таким образом давление и объем прямо пропорциональны количеству молей и температуре.
Также уравнение Клапейрона-Менделеева можно записать в ином виде:
p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 — 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:
N = m N A M , где
N A = 6 . 02 * 10 23 м о л ь — 1 ; — это постоянная Авогадро.
Какое значение имеет универсальная газовая постоянная
Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.
Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 — 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь — 1 ) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .
Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.
Связь с другими законами состояния идеального газа
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.
Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.
Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.
В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:
- изотермический процесс (T=const);
- изохорный процесс (V=const);
- изобарный процесс (p=const).
Изотермический процесс (T=const)
Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.
Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.
Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:
Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.
Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).
Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.
Рис.1. Изотерма в pV — координатах.
Изохорный процесс (V=const)
Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.
Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:
p 1 p 2 = T 1 T 2
Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.
Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда
p = p 0 T T 0 = p 0 γ T
Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.
Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).
Рис.2 Изображение изохоры в pT-координатах.
Изобарный процесс (p=const)
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.
Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.
V 1 V 2 = T 1 T 2
Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:
V = V 0 T T 0 = V 0 α T
Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.
Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.
Коэффициент α называют температурным коэффициентом объемного расширения газов.
Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).
Рис. 3. Изобара в VT-координатах.
Использование универсального уравнения для решения задачи
В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.
Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.
Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:
p V = n R T = m M R T
Не забываем перевести температуру в Кельвины:
T = t + 273 = 27 + 273 = 300 K
Молярная масса кислорода известна из таблицы Менделеева:
M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 — 3 к г / м о л ь
Выразим из уравнения состояния давления и поставим все имеющиеся данные:
p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 — 3 * 1 = 77 . 906 П а = 78 к П а
Ответ: p = 78 кПа.
Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?
Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:
p = n R T V = m R T M V
Молярная масса кислорода предполагается равной:
M ( O 2 ) = 2 * 16 = 32 г / м 3
Не забываем перевести температуру в Кельвины:
T = t + 273 = 20 + 273 = 293 K
Переводим давление: p = 15680000 Па
Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:
V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 — 3 = 3 . 1 * 10 — 2 м 3 = 31 л .
Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .
Согласно уравнению Менделеева-Клапейрона:
p = n R T V = m R T M V
Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:
ρ = m V и л и V = m ρ
Тогда p m ρ = n R T = m R T M
Откуда выражаем плотность газа:
Для водорода эта формула запишется следующим образом:
ρ H 2 = p M H 2 R T
По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:
ρ H 2 M H 2 = p R T
Поставим последнее выражение в выражение для плотности любого газа:
ρ = M * ρ H 2 M H 2
Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.
ρ = M r * ρ H 2 2
Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .
Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.
При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?
По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.
p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.
Откуда можем найти начальный объем:
p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V
V 1 ( p 1 — p 1 2 . 5 ) = p 1 2 . 5 ∆ V
p 1 2 . 5 V 1 ( 2 . 5 — 1 ) = p 1 2 . 5 ∆ V
V 1 = ∆ V 1 , 5 = 8 л
Ответ: первоначальный объем газа был равен 8 л.
Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?
Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.
При изохорном процессе:
p 1 T 1 = p 2 T 2
T 2 = p 2 T 1 p 1
p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K
При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?
Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.
V 1 V 2 = T 1 T 2
V_2 – искомый объем
Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:
T 1 = 273 + 27 = 300 K
T 2 = 273 + 57 = 330 K
T 2 V 1 T 1 = V 2
V 2 = ( 600 * 330 ) / 300 = 660 м л
Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.
Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:
V 1 V 2 = T 1 T 2
Перейдем к абсолютной температуре:
T 1 = 1150 + 273 = 1423 K
T 2 = 200 + 273 = 473 K
Масса газа: m = ρ 1 V 1 = ρ 2 V 2
Использование этих формул приводит к следующему:
источники:
http://www.eduspb.com/node/1742
http://wika.tutoronline.ru/fizika/class/10/uravnenie-klapejronamendeleeva
Уравне́ние состоя́ния идеа́льного га́за (иногда уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:
,
где
Уравнение состояния идеального газа можно записать в виде:
,
где 


или в виде
,
где 


Эта форма записи носит имя уравнения (закона) Клапейрона — Менделеева.
Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную 
Менделеев обнаружил, что 


Связь с другими законами состояния идеального газа[править | править код]
В случае постоянной массы газа уравнение можно записать в виде:
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:
— закон Бойля — Мариотта — Изотермический процесс.
— Закон Гей-Люссака — Изобарный процесс.
— закон Шарля (второй закон Гей-Люссака, 1808 г.) — Изохорный процесс
В форме пропорции 
С точки зрения химика этот закон может звучать несколько иначе: объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода:
.
1 объём азота соединяется с 3 объёмами водорода с образованием 2 объёмов аммиака:
.
- Закон Бойля — Мариотта
Закон Бойля — Мариотта
назван в честь ирландского физика, химика и философа Роберта Бойля (1627—1691), открывшего его в 1662 г., а также в честь французского физика Эдма Мариотта (1620—1684), который открыл этот закон независимо от Бойля в 1677 году.
В некоторых случаях (в газовой динамике) уравнение состояния идеального газа удобно записывать в форме
где 

Эмиль Амага обнаружил, что при высоких давлениях поведение газов отклоняется от закона Бойля — Мариотта. Это обстоятельство может быть прояснено на основании молекулярных представлений.
С одной стороны, в сильно сжатых газах размеры самих молекул являются сравнимыми с расстояниями между молекулами. Таким образом, свободное пространство, в котором движутся молекулы, меньше, чем полный объём газа. Это обстоятельство увеличивает число ударов молекул в стенку, так как благодаря ему сокращается расстояние, которое должна пролететь молекула, чтобы достигнуть стенки.
С другой стороны, в сильно сжатом и, следовательно, более плотном газе молекулы заметно притягиваются к другим молекулам гораздо большую часть времени, чем молекулы в разреженном газе. Это, наоборот, уменьшает число ударов молекул в стенку, так как при наличии притяжения к другим молекулам молекулы газа движутся по направлению к стенке с меньшей скоростью, чем при отсутствии притяжения. При не слишком больших давлениях более существенным является второе обстоятельство и произведение 

См. также[править | править код]
- Совершенный газ
- Реальный газ
- Уравнение состояния реального газа
Примечания[править | править код]
Литература[править | править код]
- Стромберг А. Г., Семченко Д. П. Физическая химия: Учеб. для хим. спец. вузов / Под ред. А. Г. Стромберга. — 7-е изд., стер. — М.: Высшая школа, 2009. — 527 с. — ISBN 978-5-06-006161-1.
Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:
Уравнение состояния идеального газа
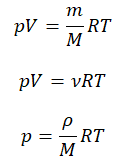
Внимание! При решении задач важно все единицы измерения переводить в СИ.
Пример №1. Кислород находится в сосуде вместимостью 0,4 м3 под давлением 8,3∙105 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.
Из основного уравнения состояния идеального газа выразим массу:
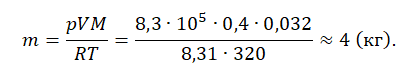
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.
Подсказки к задачам
| Давление возросло на 15% | p2 = 1,15p1 |
| Объем увеличился на 2% | V2 = 1,02V1 |
| Масса увеличилась в 3 раза | m2 = 3m1 |
| Газ нагрелся до 25 оС | T2 = 25 + 273 = 298 (К) |
| Температура уменьшилась на 15 К (15 оС) | T2 = T1 – 15 |
| Температура уменьшилась в 2 раза | |
| Масса уменьшилась на 20% | m2 = 0,8m1 |
| Выпущено 0,7 начальной массы |
Важна только та масса, что осталась в сосуде. Поэтому: m2 = 0,3m1 |
| Какую массу следует удалить из баллона? | Нужно найти разность начальной и конечной массы:
m1 – m2 |
| Газ потерял половину молекул | |
| Молекулы двухатомного газа (например, водорода), диссоциируют на атомы | |
| Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ) | M (O3) = 3Ar (O)∙10–3 кг/моль
M (O2) = 2Ar (O)∙10–3 кг/моль |
| Открытый сосуд | Объем V и атмосферное давление pатм остаются постоянными |
| Закрытый сосуд | Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины |
| Нормальные условия | Температура T0 = 273 К
Давление p0 = 105 Па |
| Единицы измерения давления | 1 атм = 105 Па |
Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.
2,8 МПа = 2,8∙106 Па
1,5 МПа = 1,5∙106 Па
Так как половина молекул была выпущена, m2 = 0,5m1. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:
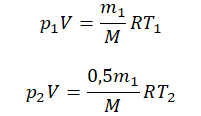
Преобразим уравнения и получим:
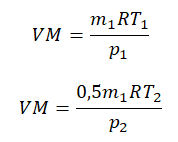
Приравняем правые части и выразим искомую величину:
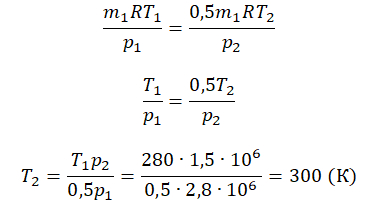
Задание EF19012
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
Ответ:
• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22473
На высоте 200 км давление воздуха составляет примерно 10–9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.
Ответ:
а) 8,31⋅ 10–11 кг/м3
б) 1,38⋅ 10–9 кг/м3
в) 3⋅ 10–10 кг/м3
г)29⋅ 10–8 кг/м3
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение Менделеева — Клапейрона.
3.Выразить из уравнения плотность.
4.Подставить известные данные и сделать вычисления.
Решение
Запишем исходные данные:
• Давление воздуха на высоте 200 км: p = 10–9∙105 Па. Или p = 10–4 Па.
• Температура воздуха на этой же высоте: T = 1200 К.
Запишем уравнение Менделеева — Клапейрона:
pV=mMRT
Плотность определяется формулой:
ρ=mV
Следовательно, масса равна произведению плотности на объем. Перепишем уравнение состояния идеального газа, учитывая, что объем сократится слева и справа:
p=ρMRT
Молярная масса воздуха — табличная величина, равная 28,97 г/моль. Переведем в СИ и получим 28,97∙10–3 кг/моль.
Выразим и вычислим плотность:
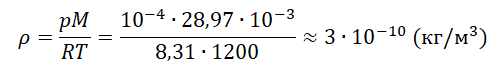
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22749
 Одноатомный идеальный газ в количестве ν моль помещают в открытый сверху сосуд под лёгкий подвижный поршень и начинают нагревать. Начальный объём газа V0, давление p0. Масса газа в сосуде остаётся неизменной. Трением между поршнем и стенками сосуда пренебречь. R– универсальная газовая постоянная.
Одноатомный идеальный газ в количестве ν моль помещают в открытый сверху сосуд под лёгкий подвижный поршень и начинают нагревать. Начальный объём газа V0, давление p0. Масса газа в сосуде остаётся неизменной. Трением между поршнем и стенками сосуда пренебречь. R– универсальная газовая постоянная.
Установите соответствие между физическими величинами, характеризующими газ, и формулами, выражающими их зависимость от абсолютной температуры T газа в условиях данной задачи.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать уравнение состояния идеального газа и выразить из него объем. Выбрать из таблицы соответствующий номер формулы.
2.Определить, от чего зависит внутренняя энергия идеального газа.
3.Записать основное уравнение МКТ и выразить внутреннюю энергию идеального газа. Выбрать из таблицы соответствующий номер формулы.
Решение
Уравнение состояния идеального газа имеет вид:
pV=mMRT
Учтем, что отношение массы к молярной массе есть количество вещества.Отсюда объем равен:
V=νRTp
Следовательно, первой цифрой ответа будет «1».
Внутренняя энергия идеального газа равна сумме кинетических энергий всех молекул этого газа:
E=N−Ek
Запишем основное уравнение МКТ:
p=nkT
Отсюда температура газа равна:
T=pnk
Но температура прямо пропорциональна средней кинетической энергии молекул газа:
T=2−Ek3k
Следовательно:
pnk=2−Ek3k
−Ek=3p2n
E=N−Ek=N3p2n
Но концентрация определяется отношением количества молекул к объему. Следовательно:
E=N3pV2N=3pV2
А произведение давления на объем можно выразить через уравнение Менделеева — Клапейрона. Следовательно:
E=32νRT
Вторая цифра ответа будет «3».
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22795
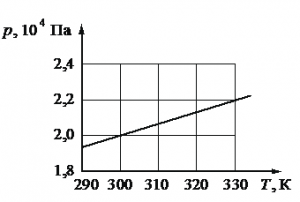 На рисунке показан график зависимости давления газа в запаянном сосуде от его температуры. Объём сосуда равен 0,25 м3. Какое приблизительно количество газообразного вещества содержится в этом сосуде? Ответ округлите до целых.
На рисунке показан график зависимости давления газа в запаянном сосуде от его температуры. Объём сосуда равен 0,25 м3. Какое приблизительно количество газообразного вещества содержится в этом сосуде? Ответ округлите до целых.
Алгоритм решения
1.Записать исходные данные.
2.Выбрать любую точку графика и извлечь из нее дополнительные данные.
3.Записать уравнение состояния идеального газа.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные. Объем сосуда равен: V = 0,25 м3. На графике выберем точку, соответствующую температуре T = 300 К. Ей соответствует давление p = 2∙104 Па.
Запишем уравнение состояния идеального газа:
pV=νRT
Отсюда количества вещества равно:
ν=pVRT=2·104·0,258,31·300≈2 (моль)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17664
Зависимость объёма идеального газа от температуры показана на VТ-диаграмме (см. рисунок). В какой из точек давление газа максимально? Масса газа постоянна.
Ответ:
A
B
C
D
Алгоритм решения
1.Записать уравнение состояния идеального газа.
2.Установить, как зависит давление от объема и температуры газа.
3.На основании графика, отображающего изменение температуры и объема газа, установить, в какой точке давление газа максимально.
Решение
Запишем уравнение состояния идеального газа:
pV=νRT
Отсюда видно, что давление прямо пропорционально температуре. Это значит, что с ростом температуры давление увеличивается.
Также видно, что давление обратно пропорционально объему. Следовательно, давление увеличивается с уменьшением объема.
Отсюда следует, что давление будет максимальным в той точке, в которой температура максимальна, а объем минимален. Такой точкой является точка D.
Ответ: D
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18093
В камере, заполненной азотом, при температуре К находится открытый цилиндрический сосуд (см. рис. 1). Высота сосуда
см. Сосуд плотно закрывают цилиндрической пробкой и охлаждают до температуры
К. В результате расстояние от дна сосуда до низа пробки становится равным h (см. рис. 2). Затем сосуд нагревают до первоначальной температуры T0. Расстояние от дна сосуда до низа пробки при этой температуре становится равным
см (см. рис. 3). Чему равно h? Величину силы трения между пробкой и стенками сосуда считать одинаковой при движении пробки вниз и вверх. Массой пробки пренебречь.

Алгоритм решения
1.Записать исходные данные и перевести единицы измерения физических величин в СИ.
2.Записать уравнение Менделеева — Клапейрона и применить его ко всем состояниям газа.
3.Определить условие равновесия пробки.
4.Выполнить решение задачи в общем виде.
5.Вычислить искомую величину.
Решение
Запишем исходные данные:
• Начальная температура азота: T0 = 300 К.
• Высота сосуда: L = 50 см.
• Температура азота после охлаждения: T1 = 240 К.
• Высота столба азота после нагревания: H = 46 см.
50 см = 0,5 м
46 см = 0,46 м
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество азота не меняется, можем принять, что:
pVT=const
Применим уравнение Менделеева — Клапейрона для всех трех состояний азота. Учтем, что
p0V0T0=p1V1T1=p2V2T2
Пусть S — площадь поперечного сечения сосуда. Тогда объемы столба азота для каждого из состояний будут равны:
V0=SL
V1=Sh
V2=SH
Известно, что в состоянии 3 температура азота поднимается до первоначальной. Поэтому уравнение Менделеева — Клапейрона примет вид:
p0SLT0=p1ShT1=p2SHT0
p0LT0=p1hT1=p2HT0
Неизвестными остались только давления. Их можно определить, записав условие равновесия пробки.
В состоянии 1 сила давления азота на пробку определяется формулой:
p0S=pатмS
В состоянии 2 на пробку действует сила давления со стороны азота и атмосферного давления, я а также сила трения, направленная вверх. Следовательно:
p1S=pатмS−Fтр=p0S−Fтр
В состоянии 3 на пробку действуют те же силы, но сила трения теперь действует не вверх, а вниз. Поэтому:
p2S=pатмS+Fтр=p0S+Fтр
Выразим из этих уравнений силу трения:
Fтр=p0S−p1S
Fтр=p2S−p0S
Приравняем правые части и получим:
p0S−p1S=p2S−p0S
Отсюда:
p0−p1=p2−p0
2p0=p2+p1
p0=p2+p12
Подставим это значение в уравнение Менделеева — Клапейрона и получим:
p2+p12LT0=p1hT1=p2HT0
Отсюда:
p2+p12L=p2H
p2L+p1L=2p2H
p1L=2p2H−p2L=p2(2H−L)
p1=p2(2H−L)L
Отсюда:
p2(2H−L)LhT1=p2HT0
Давление слева и справа взаимоуничтожается. Остается:
T0(2H−L)Lh=HT1
Отсюда выразим h:
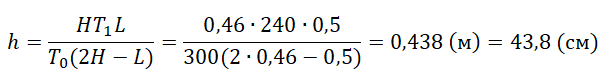
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18873
 В сосуде неизменного объёма при комнатной температуре находилась смесь неона и аргона, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль аргона. Как изменились в результате парциальное давление неона и давление смеси газов, если температура газов в сосуде поддерживалась неизменной?
В сосуде неизменного объёма при комнатной температуре находилась смесь неона и аргона, по 1 моль каждого. Половину содержимого сосуда выпустили, а затем добавили в сосуд 1 моль аргона. Как изменились в результате парциальное давление неона и давление смеси газов, если температура газов в сосуде поддерживалась неизменной?
Для каждой величины определите соответствующий характер изменения:
- увеличилась
- уменьшилась
- не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Записать исходные данные.
2.Установить характер изменения парциального давления неона.
3.Применить закон Менделеева — Клапейрона, чтобы установить характер изменения общего давления смеси газов.
Решение
Исходные данные:
• Количество неона: ν1 = 1 моль.
• Количество аргона: ν2 = 1 моль.
• Количество впущенного аргона: ν4 = 1 моль.
Сначала парциальное давление неона и аргона равно. Это объясняется тем, что давление газов при неизменном количестве вещества зависит только от объема и температуры. Эти величины постоянны.
Когда из сосуда выпустили половину газовой смеси, в нем оказалось по половине моля каждого из газов. Затем в сосуд впустили 1 моль аргона. Следовательно, в сосуде стало содержаться 0,5 моль неона и 1,5 моль аргона. Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Из уравнения видно, что давление и количество вещества — прямо пропорциональные величины. Следовательно, если количество неона уменьшилось, то его парциальное давление тоже уменьшилось.
Общая сумма количества вещества равна сумме количеств вещества 1 (неона) и 2 (аргона): 0,5 + 1,5 = 2 (моль). Изначально в сосуде тоже содержалось 2 моль газа. Так как количество вещества, температура и объем сохранились, давление тоже осталось неизменным.
Ответ: 23
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6.4k




