Фо́рмула Пла́нка (зако́н Пла́нка) — формула, описывающая спектральную плотность излучения, которое создаётся абсолютно чёрным телом определённой температуры. Формула была открыта Максом Планком в 1900 году и названа по его фамилии. Её открытие сопровождалось появлением гипотезы о том, что энергия может принимать только дискретные значения. Эта гипотеза некоторое время после открытия не считалась значимой, но, как принято считать, дала рождение квантовой физике.
Формула[править | править код]
Формула Планка — выражение для спектральной плотности излучения, создаваемого абсолютно чёрным телом определённой температуры. Встречаются различные формы записи этой формулы[1][2].
Энергетическая яркость[править | править код]
Формула, выражающая спектральную плотность энергетической яркости, выглядит следующим образом[3]:
где 








.
В этом случае 


Излучательная способность[править | править код]
Излучательная способность на частоте 





,
.
Таким образом, излучательная способность тела численно в 


Спектральная плотность энергии[править | править код]
Ещё одна форма записи описывает спектральную объёмную плотность энергии излучения абсолютно чёрного тела. По аналогии с предыдущими формулами, она равна плотности энергии в малом диапазоне частот или длин волн, делённой на ширину этого диапазона[1][2]:
,
.
В системе СИ величины 


Применимость[править | править код]
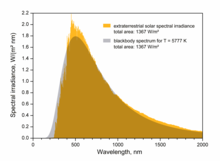
Спектр Солнца (жёлтый цвет) и спектр абсолютно чёрного тела температурой 5777 K (серый цвет)
Формула Планка применима для излучения, которое находится в тепловом равновесии с веществом при определённой температуре[2]. Она применима для абсолютно чёрных тел любой формы вне зависимости от состава и структуры при условии, что размеры излучающего тела и деталей его поверхности гораздо больше длин волн, на которых тело в основном излучает[3][7].
В случае если тело не является абсолютно чёрным, то спектр его равновесного теплового излучения не описывается законом Планка, но связан с ним законом излучения Кирхгофа. Согласно этому закону, отношение излучательной и поглощательной способностей тела одинаково для всех длин волн и зависит только от температуры[8]. Так, например, при одной температуре распределение энергии в спектре абсолютно серого тела будет таким же, как и в спектре абсолютно чёрного, но суммарная энергетическая яркость излучения будет меньше[9].
Формула Планка также используется и для описания реальных тел, спектр излучения которых отличается от планковского. Для этого вводится понятие эффективной температуры тела: это та температура, при которой абсолютно чёрное тело излучает столько же энергии на единицу площади, что и данное тело. Аналогичным образом определяется яркостная температура, равная температуре абсолютно чёрного тела, излучающего столько же энергии на единицу площади на определённой длине волны, и цветовая температура, равная температуре абсолютно чёрного тела с таким же распределением энергии в определённом участке спектра[2][10][11]. Например, для Солнца эффективная температура составляет около 5780 K, а яркостная температура, в зависимости от длины волны, принимает различные значения: на длине волны 1500 Å она достигает минимального значения в 4200 K, а в видимом диапазоне на длине волны 5500 Å составляет около 6400 K, в то время как для абсолютно чёрного тела температуры, определяемые таким образом, совпадают[12].
История открытия[править | править код]
Предыстория[править | править код]
Определение закона теплового излучения представляло интерес с 1859 года, когда Густав Кирхгоф открыл закон излучения Кирхгофа, согласно которому отношение излучательной и поглощательной способностей универсально для всех тел. Следовательно, функция излучения абсолютно чёрного тела, поглощательная способность которого равна единице для всех длин волн, должна совпадать с функцией этого отношения[13][14].
К концу XIX века спектр излучения абсолютно чёрного тела уже был известен экспериментально. В 1896 году Вильгельм Вин эмпирически описал его законом излучения Вина, однако получить ни его теоретическое обоснование, ни какой-либо вывод физикам на тот момент не удавалось. Хотя Вин в своей работе приводил обоснование закона, оно было недостаточно строгим, чтобы эта проблема считалась решённой[6][15][16].
Макс Планк был одним из тех, кто пытался теоретически обосновать закон излучения Вина. Он исходил из того, что излучатели являются линейными гармоническими осцилляторами, у которых установилось равновесие между испусканием и поглощением; определив связь между энтропией и энергией осцилляторов, он смог подтвердить закон излучения Вина[17].
Однако дальнейшие эксперименты показали, что закон излучения Вина неточно описывает спектр теплового излучения в длинноволновой области. В октябре 1900 года Планк представил формулу, которая с точностью до констант совпадала с современным законом Планка. В тот же день было выяснено, что формула хорошо описывает экспериментальные данные, но при этом она не имела под собой теоретической основы. Планк вывел её лишь на основании того, что в предельном случае для коротких волн она должна переходить в закон Вина, но, в отличие от него, согласовываться с экспериментальными данными для длинных волн[18].
Открытие[править | править код]
Менее чем через два месяца после сообщения о получении формулы Планк представил её теоретический вывод на заседании Немецкого физического общества. В нём использовалось соотношение для энтропии, введённое Людвигом Больцманом, в котором рассматривается число возможных микроскопических состояний системы. Планк, чтобы иметь возможность использовать методы комбинаторики и оценить таким образом энтропию, сделал допущение, что полная энергия состоит из целого числа конечных элементов энергии — квантов[15][19].
Несмотря на то, что в этом выводе появились кванты и была введена и впервые использована постоянная Планка, ни сам Планк, ни его коллеги не поняли всей глубины открытия. Например, Планк считал, что дискретность энергии не имеет никакого физического смысла и является лишь математическим приёмом. Другие физики также не придали этому значения и не считали, что это предположение противоречит классической физике. Лишь после публикации Хендрика Лоренца в 1908 году научное сообщество пришло к мнению, что кванты действительно имеют физический смысл. Сам Планк впоследствии называл ввод квантов «актом отчаяния», вызванным тем, что «теоретическое объяснение должно быть найдено любой ценой, сколь высокой она ни была бы». Несмотря на всё это, день, когда формула Планка была обоснована, — 14 декабря 1900 года — считается днём рождения квантовой физики[15][20].
Пользуясь соображениями классической физики, в 1900 году лорд Рэлей, а в 1905 году Джеймс Джинс вывели закон Рэлея — Джинса. К такому же результату, независимо от них, приходил в своих работах и сам Планк. Вывод этого закона мало отличался от вывода закона Планка (см. ниже[⇨]), за исключением того, что средняя энергия излучения 

В 1918 году Макс Планк стал лауреатом Нобелевской премии по физике, и хотя официально он был награждён за открытие квантов, это открытие было тесно связано с выводом закона Планка[22].
Вывод формулы Планка[править | править код]
Вывод через распределение Больцмана[править | править код]
Формула Планка выводится следующим образом[6].
При выводе рассматривается абсолютно чёрное тело малых размеров с температурой 




При выборе малой площади 







.
Суммой энергии, приходящей со всех направлений, будет поток 
.
Такое же количество энергии будет излучать та же единица площади абсолютно чёрного тела, а значит, как для всего потока, так и для любого диапазона частот или длин волн будет справедливо соотношение 
Так как внутри куба одновременно присутствуют и излучаемые, и отражённые волны, поле теплового излучения должно представлять собой их суперпозицию, то есть иметь вид стоячих электромагнитных волн. Для определения их параметров вводятся декартова система координат вдоль рёбер куба и соответствующие орты 







Для волн, распространяющихся вдоль осей 






С помощью безразмерной величины 






где 

.
Если продифференцировать это выражение по частоте, получится число стоячих волн с длинами волн в интервале 
.
Можно взять за 





.
Для дальнейшего вывода закона Планка необходимо учитывать эффекты квантовой физики, а именно — то, что энергия излучается конечными по величине порциями, по величине равными 




где 


.
С учётом 

.
Таким образом, 
.
Здесь 

,
.
Получается выражение для средней энергии:
.
Если подставить 
.
Соотношение 
.
Если разделить на 
.
Эти величины можно выразить через другие параметры — например, циклическую частоту 







,
,
.
Аналогичным образом получаются формулы для длин волн. После замены 

,
,
.
Вывод через статистику Бозе — Эйнштейна[править | править код]
Если рассматривать равновесное излучение как фотонный газ, к нему можно применить статистику Бозе — Эйнштейна. Она определяет среднее число частиц 


.
В этой формуле 
.
Если умножить среднее число фотонов 



Вывод через спонтанное и вынужденное излучения[править | править код]
Формула Планка также может быть выведена из рассмотрения механизмов спонтанного и вынужденного излучений атомов[25].
В этом выводе, предложенном Эйнштейном в 1916 году, рассматриваются 













Величины 

.
В пределе 




Можно воспользоваться распределением Больцмана[25]:
.
При применении его к условию равновесия получается[25]:
где 
,
.
Энергетические уровни могут быть взяты произвольным образом, поэтому индексы 



Связь с другими формулами[править | править код]
Закон Рэлея — Джинса[править | править код]
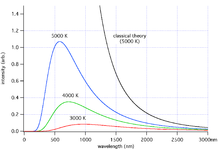
Синим и чёрным цветами обозначены спектры, соответствующие закону Планка и закону Рэлея — Джинса при одной температуре. Видно, что во втором случае наблюдается неограниченный рост мощности при уменьшении длины волны
Закон Рэлея — Джинса — приближение закона Планка, хорошо работающее при 




.
В рамках классической физики в результате вывода закона излучения получается именно закон Рэлея — Джинса. Однако при малых длинах волн закон Рэлея — Джинса не только расходится с экспериментом, но и предсказывает неограниченный рост мощности излучения при приближении длины волны к нулю. Этот парадокс получил название ультрафиолетовой катастрофы (см. выше[⇨])[6][27].
Закон излучения Вина[править | править код]
Спектры излучения по закону Планка (зелёный), в приближении Рэлея — Джинса (красный) и в приближении Вина (синий). Оси имеют логарифмический масштаб; температура тела — 0,008 К
Закон излучения Вина — приближение закона Планка, хорошо работающее при 


.
Закон Стефана — Больцмана[править | править код]
Плотность потока энергии соответствует площади под графиком функции. По закону Стефана — Больцмана она пропорциональна четвёртой степени температуры
Закон Стефана — Больцмана — выражение, описывающее излучение абсолютно чёрного тела во всём электромагнитном диапазоне. Оно выводится из закона Планка интегрированием по частоте или, в зависимости от формы записи, по длине волны[28]:
,
.
Заменим 

.
Этот определённый интеграл равен 


.
Плотность потока энергии при этом в 



Закон смещения Вина[править | править код]
По закону смещения Вина длина волны, на которой достигается максимальная излучательная способность, обратно пропорциональна температуре
Закон смещения Вина связывает длину волны, на которой излучательная способность абсолютно чёрного тела максимальна, с его температурой. Он выводится из закона Планка дифференцированием его по частоте или длине волны, в зависимости от формы записи, и приравниванием производной к нулю, который достигается в максимуме функции. При этом получается соотношение 

Хотя для частот можно проделать аналогичную процедуру, частоту максимума спектральной плотности нельзя рассчитать по формуле 
Применение[править | править код]
Для абсолютно чёрного тела спектр описываемый законом Планка однозначно связан с его температурой. Поэтому закон находит применение в пирометрии, то есть дистанционном определении температуры горячих тел. В случае отличия спектра тела от излучения абсолютно чёрного тела пирометр измеряет эффективную температуру, которая называется радиационной 



Примечания[править | править код]
- ↑ 1 2 3 Planck’s radiation law (англ.). Encyclopedia Britannica. Дата обращения: 18 декабря 2020. Архивировано 13 декабря 2020 года.
- ↑ 1 2 3 4 5 Масалов А. В. Планка закон излучения // Большая российская энциклопедия. — Издательство БРЭ, 2014. — Т. 26. — 767 с. — ISBN 978-5-85270-363-7.
- ↑ 1 2 3 4 5 6 Karttunen et al., 2007, p. 103.
- ↑ 1 2 Кононович, Мороз, 2004, с. 170.
- ↑ 1 2 Кононович, Мороз, 2004, с. 181.
- ↑ 1 2 3 4 5 6 1.2. Квантовая теория излучения. Кафедра физики МГТУ им. Баумана. Дата обращения: 18 декабря 2020. Архивировано 28 сентября 2015 года.
- ↑ Juan Carlos Cuevas. Thermal radiation from subwavelength objects and the violation of Planck’s law (англ.) // Nature Communications. — Nature Research, 2019. — 26 July (vol. 10). — P. 3342. — ISSN 2041-1723. — doi:10.1038/s41467-019-11287-6. Архивировано 12 марта 2022 года.
- ↑ 1.1. Законы теплового излучения. Кафедра физики МГТУ им. Баумана. Дата обращения: 24 января 2021. Архивировано 8 августа 2020 года.
- ↑ Серое тело. Энциклопедия физики и техники. Дата обращения: 24 января 2021. Архивировано 17 апреля 2021 года.
- ↑ Karttunen et al., 2007, p. 104.
- ↑ Кононович, Мороз, 2004, с. 193—194.
- ↑ Кононович, Мороз, 2004, с. 239—240.
- ↑ Джеммер, 1985, с. 14—16.
- ↑ Сивухин, 2002, с. 681—682.
- ↑ 1 2 3 4 Max Planck: the reluctant revolutionary (англ.). Physics World (1 декабря 2000). Дата обращения: 19 декабря 2020. Архивировано 6 июля 2022 года.
- ↑ Джеммер, 1985, с. 21.
- ↑ Джеммер, 1985, с. 22—27.
- ↑ Джеммер, 1985, с. 27—30.
- ↑ Джеммер, 1985, с. 30—33.
- ↑ Джеммер, 1985, с. 30—34.
- ↑ Сивухин, 2002, с. 697.
- ↑ The Nobel Prize in Physics 1918 (англ.). NobelPrize.org. Nobel Foundation. Дата обращения: 19 декабря 2020. Архивировано 7 июня 2020 года.
- ↑ 1 2 3 Different Formulations of Planck’s Law. www.physics-in-a-nutshell.com. Дата обращения: 19 декабря 2020. Архивировано 14 декабря 2020 года.
- ↑ 1 2 3 Сивухин, 2002, с. 703—704.
- ↑ 1 2 3 4 5 6 7 8 Сивухин, 2002, с. 704—706.
- ↑ 1 2 Кононович, Мороз, 2004, с. 182.
- ↑ 1 2 3 Karttunen et al., 2007, p. 105.
- ↑ 1 2 3 4 Karttunen et al., 2007, pp. 103—104.
- ↑ 1 2 Karttunen et al., 2007, pp. 104—105.
- ↑ Ландсберг, 2003, с. 639.
Литература[править | править код]
- Кононович Э. В.; Мороз В. И. Общий курс астрономии / Под ред. В. В. Иванова. — 2-е, испр. — М.: Едиториал УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
- Сивухин Д. В. Общий курс физики. — М.: Физматлит МФТИ, 2002. — Т. 4. Оптика. — 792 с. — ISBN 5-9221-0228-1.
- Джеммер М. Эволюция понятий квантовой механики. — М.: Наука, 1985. — 384 с.
- Ельяшевич М. А. Планка закон излучения // Физическая энциклопедия. — М.: БРЭ, 1992. — Т. 3. — С. 625—626.
- Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 5th Edition. — Berlin: Springer, 2007. — 510 p. — ISBN 978-3-540-34143-7.
- Ландсберг Г. С. Оптика: учебное пособие для вузов. — 6-е изд. стереот.. — М.: Физматлит, 2003. — 848 с. — ISBN 5-9221-0314-8.
From Wikipedia, the free encyclopedia
In radiometry, radiant energy density is the radiant energy per unit volume.[1] The SI unit of radiant energy density is the joule per cubic metre (J/m3).
Mathematical definition[edit]
Radiant energy density, denoted we (“e” for “energetic”, to avoid confusion with photometric quantities), is defined as[2]
where
- ∂ is the partial derivative symbol;
- Qe is the radiant energy;
- V is the volume.
Relation to other radiometric quantities[edit]
Because radiation always transmits the energy,[2] it is useful to wonder what the speed of the transmission is. If all the radiation at given location propagates in the same direction, then the radiant flux through a unit area perpendicular to the propagation direction is given by the irradiance:[2]
where c is the radiation propagation speed.
Contrarily if the radiation intensity is equal in all directions, like in a cavity in a thermodynamic equilibrium, then the energy transmission is best described by radiance:[3]
Radiant exitance through a small opening from such a cavity is:[4]
These relations can be used for example in the black-body radiation equation’s derivation.
SI radiometry units[edit]
| Quantity | Unit | Dimension | Notes | ||
|---|---|---|---|---|---|
| Name | Symbol[nb 1] | Name | Symbol | Symbol | |
| Radiant energy | Qe[nb 2] | joule | J | M⋅L2⋅T−2 | Energy of electromagnetic radiation. |
| Radiant energy density | we | joule per cubic metre | J/m3 | M⋅L−1⋅T−2 | Radiant energy per unit volume. |
| Radiant flux | Φe[nb 2] | watt | W = J/s | M⋅L2⋅T−3 | Radiant energy emitted, reflected, transmitted or received, per unit time. This is sometimes also called “radiant power”, and called luminosity in Astronomy. |
| Spectral flux | Φe,ν[nb 3] | watt per hertz | W/Hz | M⋅L2⋅T−2 | Radiant flux per unit frequency or wavelength. The latter is commonly measured in W⋅nm−1. |
| Φe,λ[nb 4] | watt per metre | W/m | M⋅L⋅T−3 | ||
| Radiant intensity | Ie,Ω[nb 5] | watt per steradian | W/sr | M⋅L2⋅T−3 | Radiant flux emitted, reflected, transmitted or received, per unit solid angle. This is a directional quantity. |
| Spectral intensity | Ie,Ω,ν[nb 3] | watt per steradian per hertz | W⋅sr−1⋅Hz−1 | M⋅L2⋅T−2 | Radiant intensity per unit frequency or wavelength. The latter is commonly measured in W⋅sr−1⋅nm−1. This is a directional quantity. |
| Ie,Ω,λ[nb 4] | watt per steradian per metre | W⋅sr−1⋅m−1 | M⋅L⋅T−3 | ||
| Radiance | Le,Ω[nb 5] | watt per steradian per square metre | W⋅sr−1⋅m−2 | M⋅T−3 | Radiant flux emitted, reflected, transmitted or received by a surface, per unit solid angle per unit projected area. This is a directional quantity. This is sometimes also confusingly called “intensity”. |
| Spectral radiance Specific intensity |
Le,Ω,ν[nb 3] | watt per steradian per square metre per hertz | W⋅sr−1⋅m−2⋅Hz−1 | M⋅T−2 | Radiance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅sr−1⋅m−2⋅nm−1. This is a directional quantity. This is sometimes also confusingly called “spectral intensity”. |
| Le,Ω,λ[nb 4] | watt per steradian per square metre, per metre | W⋅sr−1⋅m−3 | M⋅L−1⋅T−3 | ||
| Irradiance Flux density |
Ee[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux received by a surface per unit area. This is sometimes also confusingly called “intensity”. |
| Spectral irradiance Spectral flux density |
Ee,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Irradiance of a surface per unit frequency or wavelength. This is sometimes also confusingly called “spectral intensity”. Non-SI units of spectral flux density include jansky (1 Jy = 10−26 W⋅m−2⋅Hz−1) and solar flux unit (1 sfu = 10−22 W⋅m−2⋅Hz−1 = 104 Jy). |
| Ee,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | ||
| Radiosity | Je[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux leaving (emitted, reflected and transmitted by) a surface per unit area. This is sometimes also confusingly called “intensity”. |
| Spectral radiosity | Je,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiosity of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m−2⋅nm−1. This is sometimes also confusingly called “spectral intensity”. |
| Je,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | ||
| Radiant exitance | Me[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux emitted by a surface per unit area. This is the emitted component of radiosity. “Radiant emittance” is an old term for this quantity. This is sometimes also confusingly called “intensity”. |
| Spectral exitance | Me,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiant exitance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m−2⋅nm−1. “Spectral emittance” is an old term for this quantity. This is sometimes also confusingly called “spectral intensity”. |
| Me,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | ||
| Radiant exposure | He | joule per square metre | J/m2 | M⋅T−2 | Radiant energy received by a surface per unit area, or equivalently irradiance of a surface integrated over time of irradiation. This is sometimes also called “radiant fluence”. |
| Spectral exposure | He,ν[nb 3] | joule per square metre per hertz | J⋅m−2⋅Hz−1 | M⋅T−1 | Radiant exposure of a surface per unit frequency or wavelength. The latter is commonly measured in J⋅m−2⋅nm−1. This is sometimes also called “spectral fluence”. |
| He,λ[nb 4] | joule per square metre, per metre | J/m3 | M⋅L−1⋅T−2 | ||
| See also: SI · Radiometry · Photometry |
- ^ Standards organizations recommend that radiometric quantities should be denoted with suffix “e” (for “energetic”) to avoid confusion with photometric or photon quantities.
- ^ a b c d e Alternative symbols sometimes seen: W or E for radiant energy, P or F for radiant flux, I for irradiance, W for radiant exitance.
- ^ a b c d e f g Spectral quantities given per unit frequency are denoted with suffix “ν” (Greek letter nu, not to be confused with a letter “v”, indicating a photometric quantity.)
- ^ a b c d e f g Spectral quantities given per unit wavelength are denoted with suffix “λ“.
- ^ a b Directional quantities are denoted with suffix “Ω”.
References[edit]
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”) (1997). Online corrected version: (2006–) “Radiant energy density”. doi:10.1351/goldbook.goldbook.R05040
- ^ a b c Karel Rusňák. Přenos energie elektromagnetickým vlněním. Department of Physics, Faculty of Applied Sciences, University of West Bohemia. 2005-11. Visited 2013-10-06
- ^ Max Planck. The Theory of Heat Radiation. Equation 21. 1914.
- ^ Max Planck. The Theory of Heat Radiation. Equation 7. 1914.
| Энергия излучения | |
 |
|
| Размерность |
M.L2T-2 |
|---|---|
| Единицы измерения | |
| СИ |
Дж |
| СГС |
эрг |
| Примечания | |
|
скалярная величина |
Эне́ргия излуче́ния — физическая величина, одна из основных энергетических фотометрических величин. Представляет собой энергию, переносимую оптическим излучением[1]. Служит основой для других энергетических фотометрических величин.
Единицей измерения в Международной системе единиц (СИ) является джоуль (Дж), в системе СГС — эрг (эрг).
В качестве буквенного обозначения используется[1][2] 

В системе световых величин аналогом энергии излучения является световая энергия 
Спектральная плотность энергии излучения
Если излучение немонохроматично, то во многих случаях оказывается полезным использовать такую величину, как спектральная плотность энергии излучения. Спектральная плотность энергии излучения представляет собой энергию излучения, приходящуюся на малый единичный интервал спектра[2]. Точки спектра при этом могут задаваться их длинами волн, частотами, энергиями квантов излучения, волновыми числами или любым другим способом. Если переменной, определяющей положение точек спектра, является некоторая величина 




Соответственно, в случае использования длин волн для спектральной плотности энергии излучения будет выполняться:
а при использовании частоты —
Следует иметь в виду, что значения спектральной плотности энергии излучения в одной и той же точке спектра, получаемые при использовании различных спектральных координат, друг с другом не совпадают. То есть, например, 
-
и
правильное соотношение приобретает вид:
Световой аналог
В системе световых фотометрических величин аналогом для энергии излучения является световая энергия 

где 
Производные величи́ны
Сведения об основных энергетических величинах приведены в таблице[7].
Энергетические фотометрические величины СИ
| Наименование (синоним[8]) | Обозначение величины | Определение | Обозначение единиц СИ | Световой аналог |
|---|---|---|---|---|
| Поток излучения (лучистый поток) |
 e или e или 
|

|
Вт | Световой поток |
| Сила излучения (энергетическая сила света) |

|

|
Вт·ср−1 | Сила света |
| Объёмная плотность энергии излучения |

|

|
Дж·м−3 | Объёмная плотность световой энергии |
| Энергетическая светимость |

|

|
Вт·м−2 | Светимость |
| Энергетическая яркость |

|

|
Вт·м−2·ср−1 | Яркость |
| Интегральная энергетическая яркость |

|

|
Дж·м−2·ср−1 | Интегральная яркость |
| Облучённость (энергетическая освещённость) |

|

|
Вт·м−2 | Освещённость |
| Энергетическая экспозиция |

|

|
Дж·м−2 | Световая экспозиция |
| Спектральная плотность энергии излучения |

|

|
Дж·м−1 | Спектральная плотность световой энергии |
Здесь 


Примечания
- ↑ 1 2 ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин
- ↑ 1 2 ГОСТ 26148—84. Фотометрия. Термины и определения.
- ↑ ГОСТ 8.332-78. Государственная система обеспечения единства измерений. Световые измерения. Значения относительной cпектральной световой эффективности монохроматического излучения для дневного зрения.
- ↑ В литературе используется также термин «фотометрический эквивалент излучения».
- ↑ Число 683 лм/Вт является приближённым значением
, более точное значение – 683,002 лм/Вт. Подробности приведены в статье Кандела.
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин.
- ↑ Все обозначения по ГОСТ 7601-78 и ГОСТ 26148—84.
- ↑ Наименование, используемое в литературе, но не входящее в число рекомендованных в системе СИ и в ГОСТах.
| Энергия излучения | |
|---|---|
| [math]displaystyle{ Q_e, W }[/math] | |
| Размерность | M.L2T-2 |
| Единицы измерения | |
| СИ | Дж |
| СГС | эрг |
| Примечания | |
| скалярная величина |
Эне́ргия излуче́ния — физическая величина, одна из основных энергетических фотометрических величин. Представляет собой энергию, переносимую оптическим излучением[1]. Служит основой для других энергетических фотометрических величин.
Единицей измерения в Международной системе единиц (СИ) является джоуль (Дж), в системе СГС — эрг (эрг).
В качестве буквенного обозначения используется[1][2] [math]displaystyle{ Q_e }[/math] или [math]displaystyle{ W }[/math].
В системе световых величин аналогом энергии излучения является световая энергия [math]displaystyle{ Q_v }[/math].
Спектральная плотность энергии излучения
Если излучение немонохроматично, то во многих случаях оказывается полезным использовать такую величину, как спектральная плотность энергии излучения.
Спектральная плотность энергии излучения представляет собой энергию излучения, приходящуюся на малый единичный интервал спектра[2]. Точки спектра при этом могут задаваться их длинами волн, частотами, энергиями квантов излучения, волновыми числами или любым другим способом. Если переменной, определяющей положение точек спектра, является некоторая величина [math]displaystyle{ x }[/math], то соответствующая ей спектральная плотность энергии излучения обозначается [math]displaystyle{ Q_{e,x}(x) }[/math] и определяется как отношение величины [math]displaystyle{ dQ_e(x), }[/math] приходящейся на малый спектральный интервал, заключённый между [math]displaystyle{ x }[/math] и [math]displaystyle{ x+dx, }[/math] к ширине этого интервала:
-
- [math]displaystyle{ Q_{e,x}(x)=frac{dQ_e(x)}{dx}. }[/math]
Соответственно, в случае использования длин волн для спектральной плотности энергии излучения будет выполняться:
-
- [math]displaystyle{ Q_{e,lambda}(lambda)=frac{dQ_e(lambda)}{dlambda}, }[/math]
а при использовании частоты —
-
- [math]displaystyle{ Q_{e,nu}(nu)=frac{dQ_e(nu)}{dnu}. }[/math]
Следует иметь в виду, что значения спектральной плотности энергии излучения в одной и той же точке спектра, получаемые при использовании различных спектральных координат, друг с другом не совпадают. То есть, например, [math]displaystyle{ Q_{e,nu}(nu)ne Q_{e,lambda}(lambda). }[/math] Нетрудно показать, что с учетом
-
- [math]displaystyle{ Q_{e,nu}(nu)=frac{dQ_e(nu)}{dnu}=frac{dlambda}{dnu}frac{dQ_e(lambda)}{dlambda} }[/math] и [math]displaystyle{ lambda=frac{c}{nu} }[/math]
правильное соотношение приобретает вид:
-
- [math]displaystyle{ Q_{e,nu}(nu)=frac{lambda^2}{c}Q_{e,lambda}(lambda). }[/math]
Световой аналог
В системе световых фотометрических величин аналогом для энергии излучения является световая энергия [math]displaystyle{ Q_v }[/math]. По отношению к энергии излучения световая энергия является редуцированной фотометрической величиной, получаемой с использованием значений относительной спектральной световой эффективности монохроматического излучения для дневного зрения [math]displaystyle{ V(lambda) }[/math][3]:
-
- [math]displaystyle{ Q_v=K_m cdot intlimits_{380~nm}^{780~nm}Q_{e,lambda}(lambda)V(lambda) dlambda, }[/math]
где [math]displaystyle{ K_m }[/math] — максимальная световая эффективность излучения[4], равная в системе СИ 683 лм/Вт[5][6]. Её численное значение следует непосредственно из определения канделы.
Производные величины
Сведения об основных энергетических величинах приведены в таблице[7].
Энергетические фотометрические величины СИ
| Наименование (синоним[8]) | Обозначение величины | Определение | Обозначение единиц СИ | Световой аналог |
|---|---|---|---|---|
| Поток излучения (лучистый поток) | [math]displaystyle{ Phi }[/math]e или [math]displaystyle{ P }[/math] | [math]displaystyle{ Phi_e=frac{dQ_e}{dt} }[/math] | Вт | Световой поток |
| Сила излучения (энергетическая сила света) | [math]displaystyle{ I_e }[/math] | [math]displaystyle{ I_e=frac{dPhi_e}{dOmega} }[/math] | Вт·ср−1 | Сила света |
| Объёмная плотность энергии излучения | [math]displaystyle{ U_e }[/math] | [math]displaystyle{ U_e=frac{dQ_e}{dV} }[/math] | Дж·м−3 | Объёмная плотность световой энергии |
| Энергетическая светимость | [math]displaystyle{ M_e }[/math] | [math]displaystyle{ M_e=frac{dPhi_e}{dS_1} }[/math] | Вт·м−2 | Светимость |
| Энергетическая яркость | [math]displaystyle{ L_e }[/math] | [math]displaystyle{ L_e=frac{d^2Phi_e}{dOmega,dS_1,cosvarepsilon} }[/math] | Вт·м−2·ср−1 | Яркость |
| Интегральная энергетическая яркость | [math]displaystyle{ Lambda_e }[/math] | [math]displaystyle{ Lambda_e=int_0^t L_e(t’) dt’ }[/math] | Дж·м−2·ср−1 | Интегральная яркость |
| Облучённость (энергетическая освещённость) | [math]displaystyle{ E_e }[/math] | [math]displaystyle{ E_e=frac{dPhi_e}{dS_2} }[/math] | Вт·м−2 | Освещённость |
| Энергетическая экспозиция | [math]displaystyle{ H_e }[/math] | [math]displaystyle{ H_e=frac{dQ_e}{dS_2} }[/math] | Дж·м−2 | Световая экспозиция |
| Спектральная плотность энергии излучения | [math]displaystyle{ Q_{e,lambda} }[/math] | [math]displaystyle{ Q_{elambda}=frac{dQ_e}{dlambda} }[/math] | Дж·м−1 | Спектральная плотность световой энергии |
Здесь [math]displaystyle{ dS_1 }[/math] — площадь элемента поверхности источника,
[math]displaystyle{ dS_2 }[/math] — площадь элемента поверхности приёмника,
[math]displaystyle{ varepsilon }[/math] — угол между нормалью к элементу поверхности источника и направлением наблюдения.
Примечания
- ↑ 1,0 1,1 ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин
- ↑ 2,0 2,1 ГОСТ 26148—84. Фотометрия. Термины и определения.
- ↑ ГОСТ 8.332-78. Государственная система обеспечения единства измерений. Световые измерения. Значения относительной спектральной световой эффективности монохроматического излучения для дневного зрения. (недоступная ссылка). Дата обращения: 12 июня 2012. Архивировано 4 октября 2013 года.
- ↑ В литературе используется также термин «фотометрический эквивалент излучения».
- ↑ Число 683 лм/Вт является приближённым значением [math]displaystyle{ K_m }[/math], более точное значение – 683,002 лм/Вт. Подробности приведены в статье Кандела.
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин. (недоступная ссылка). Дата обращения: 12 июня 2012. Архивировано 10 ноября 2012 года.
- ↑ Все обозначения по ГОСТ 7601-78 и ГОСТ 26148—84.
- ↑ Наименование, используемое в литературе, но не входящее в число рекомендованных в системе СИ и в ГОСТах.




















































 и
и 


