Как найти плотность газа парциальное давление

Была ли эта статья полезной?

Вопросы: Состав и физико-химические
свойства природных газов, их классификация.
Газовые смеси, плотность газов, состав
газовой смеси. Парциальные давление и
объём в смеси идеальных газов. Аналитические
методы расчета физических свойств
природных газов. Вязкость газа

Состав и физико-химические свойства природных газов. Классификация природных газов

Природные газы, добываемые из чисто
газовых, нефтяных и газоконденсатных
месторождений, состоят из углеводородов
гомологического ряда метана (С_nН_2n+2), а также неуглеводородных
компонентов: азота (N₂),
углекислого газа (СО₂), сероводорода
(H₂S),
редкоземельных (инертных) газов (гелия,
аргона, криптона, ксенона), ртути. Число
углеродных атомов n в молекуле углеводородов
может достигать 17 и более.

Метан
(СН₄),
этан (С₂Н₆)
и этилен (С₂Н₄)
при нормальных условиях (Р = 0,1 МПа и T =
273 К) являются реальными газами. Пропан
(С₃Н₈),
пропилен (С₃Н₆),
изобутан (i-C₄H₁₀),
нормальный бутан (n-С₄Н₁₀),
бутилены C₄Н₈)
при атмосферных условиях находятся в
парообразном (газообразном) состоянии,
при повышенных давлениях – в жидком. Они
входят в состав жидких (сжижаемых,
сжиженных) углеводородных газов.

Углеводороды, начиная с изопентана
(i-C₅H₁₂)
и более тяжелые (17 > n > 5) при атмосферных
условиях находятся в жидком состоянии.
Они входят в состав бензиновой фракции.
Углеводороды, молекула которых состоит
из 18 и более атомов углерода (отC₁₈H₃₈),
расположенных в одну цепочку, при
атмосферных условиях находятся в твердом
состоянии.

Природные газы подразделяются на три
группы:

1. Сухой газ, свободный от тяжелых
углеводородов, добываемый из чисто
газовых месторождений.

2. Смесь сухого газа, пропанобутановой
фракции (сжиженного газа) и газового
бензина, добываемые вместе с нефтью.

3. Сухой газ и жидкий углеводородный
конденсат, добываемые из газоконденсатных
месторождений.

Углеводородный конденсат состоит из
большого числа тяжелых углеводородов,
из которых можно выделить бензиновые,
лигроиновые, керосиновые, а иногда и
более тяжелые маслянистые фракции.

Следует отметить, что в промышленности
используются искусственные газы,
полученные из твердых топлив (горючие
сланцы, бурый уголь и пр.).

Газовые смеси. Плотность газов

Под плотностью, или объёмной массой,
тела понимают отношение массы тела в
состоянии покоя к его объёму.

Плотность газа
в нормальных физических условиях (при
0,1013 МПа и 273 К) можно определить по формуле

(1)

где М –молекулярная масса.

Если плотность газа задана при давлении
0,1013 МПа, то пересчёт её на другое давление
(при той же температуре) для идеального
газа проводится по формуле

(2)

где Р – давление, МПа.

Часто для характеристики газа применяют
относительную плотность его по воздуху
при нормальных условиях (0,1013 МПа и 273 К)

(3)

Коммерческие расчёты в газовой
промышленности проводят при стандартных
физических условиях – 0,1013 МПа и 293 К.

Состав газовой смеси

Газовые смеси (как и смеси жидкостей и
паров) характеризуются массовыми или
молярными концентрациями компонентов.
Объёмный состав газовой смеси примерно
совпадает с молярным, так как объёмы 1
кмоля идеальных газов при одинаковых
физических условиях по закону Авогадро
имеют одно и то же численное значение,
в частности при 273 К и 0,1013 МПа составляют
22,41 м³.

Для характеристики газовой смеси следует
знать её среднюю молекулярную массу,
среднюю плотность (в кг/м³) или
относительную плотность по воздуху.

Если известен молярный состав смеси в
процентах, то среднюю молекулярную
массу вычисляют по формуле

(4)

где у₁, у₂, …,у_n—молярные
(объёмные) доли компонентов, %;

M_l,
М₂, …, M_n– молекулярные массы
компонентов.

Если
задан массовый состав смеси, то её
среднюю молекулярную массу определяют
по формуле

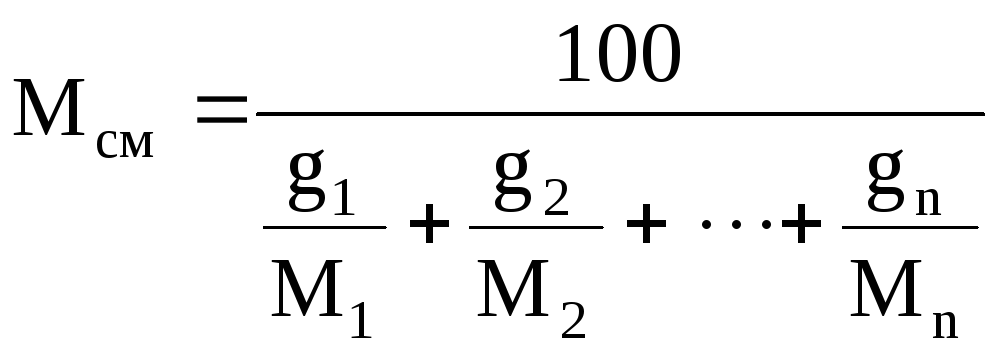(5)

где g₁,g₂,
…,g_n—массовые
доли компонентов, %.

Плотность смеси ρ_см определяется
по вычисленному значению средней
молекулярной массы М_смпо формуле,
аналогичной (1)

(6)

Относительную
плотность смеси вычисляют по формуле

(7)

где ρ_cми ρ_в— плотности соответственно смеси и
воздуха при 273 К и 0,1013 МПа.

Парциальные
давление и объём компонента в смеси
идеальных газов

Смеси
идеальных газов характеризуются
аддитивностью
парциальных давлений и парциальных
объёмов. Это означает, что каждый газ в
смеси идеальных ведет себя так, как если
бы в данном объёме он был бы один.

Парциальное давление газа – давление
газа, входящего в состав газовой смеси,
которое он оказывал бы, занимая один
весь объём смеси и находясь при неизменных
первоначальных объёме и температуре.

Парциальный объём – объём, который
занимал бы газ, входящий в состав газовой
смеси, если бы он находился при тех же
давлении и температуре, что и вся смесь.

Аддитивность
парциальных давлений выражается законом
Дальтона, согласно которому

(8)

где р – общее давление смеси
газов;

p_i –парциальное давление
i-го компонента в смеси;

(9)

или

(10)

где n_i
– число молей i-го компонента в смеси;

N – общее число молей смеси;

у_i –
n_i/N–молярная доля i-го компонента в
смеси.

Таким образом, парциальное давление
компонента р_iв смеси
идеальных газов равно произведению его
молярной доли в смесиy_iна общее давление смеси газовр.

Аддитивность парциальных объёмов
компонентов газовой смеси выражается
законом Амага, согласно которому

(11)

где V– общий объём смеси;

V_i, – парциальный объём
i-го компонента в смеси.

(12)

или

(13)

Таким образом, парциальный объём
компонента в смеси идеальных газов; V_i
–равен произведению его
молярной долиу_i в
смеси на общий объёмVсмеси газов.

Аналитические
методы расчета физических свойств
природных газов

Для определения многих физических
свойств природных газов используют
уравнение состояния – аналитическую
зависимость между параметрами,
описывающими изменение

простого или сложного вещества (давление,
объём и температура).

Клапейрон и Менделеев предложили
следующее уравнение состояния идеальных
газов:

(14)

где р – абсолютное давление. Па;

V –объём, м³;

G– масса вещества, кг;

Т– абсолютная температура, К;

R – удельная
газовая постоянная, Дж/(кг К).

Идеальным называется газ, собственный
объём молекул, которого пренебрежимо
мал по сравнению с объёмом, занимаемым
газом, и когда отсутствует взаимодействие
между молекулами.

С термодинамической точки зрения
идеальным называется газ, для которого
справедливо равенство

(15)

где Е – внутренняя энергия парообразования,
Дж/моль или

(16)

где z – коэффициент
отклонения реального газа от закона
идеального.

Экспериментальная проверка уравнения
(14), проведенная многими исследователями,
показала, что изменение свойств реальных
газов при высоких давлениях нельзя
описать зависимостью (16).

Голландский физик Ван-дер-Ваальс в 1879
г. предложил учесть собственный объём
молекул газа и силы их взаимного
притяжения посредством введения
дополнительных членов в уравнение
Клапейрона – Менделеева:

(17)

где v – V/G– удельный объем газа, м³/кг;

а/v²– константа сцепления
молекул. Па;

b– поправка на собственный объём
молекул, м³.

В уравнении (17) слагаемое а/v²,выражает внутреннее давление, которое
является как бы равнодействующей сил
притяжения всех молекул в объёмеV.Оно прибавляется к внешнему давлению.
Это уравнение приближенное.

В соотношениях для критического состояния
вещества

(18)

коэффициенты aиbвыражаются
через критическое давлениер_кри критическую температуруТ_кр
следующим образом:

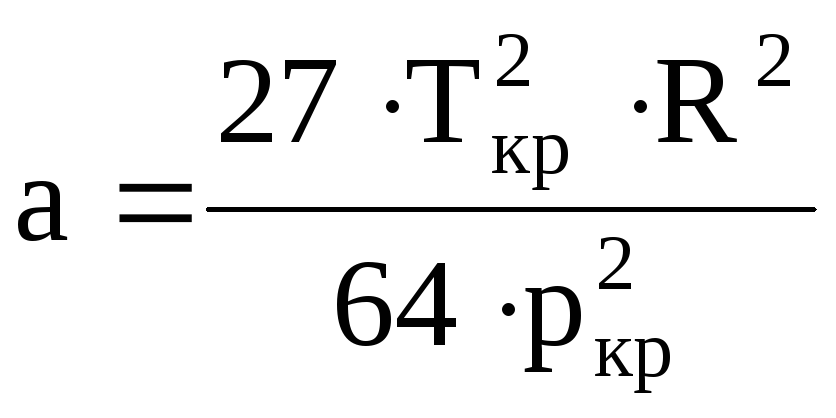;(19)

Ван-дер-Ваальс нашел, что поправка bна собственный объём молекул, имеющих
шарообразную форму, равна учетверённому
объёму молекул.

Уравнение (17) приближенное. Коэффициенты
аиbв действительности
являются сложными функциями объёма,
температуры, формы молекул газа.

Критическая температура чистого вещества
– это максимальная температура, при
которой жидкая и паровая фазы могут
сосуществовать в равновесии, или та
температура, при которой средняя
молекулярная кинетическая энергия
становится равной потенциальной энергии
притяжения молекул. При более высокой
температуре существование жидкой фазы
невозможно.

Давление
паров вещества при критической температуре
называется критическим давлением, а
объём вещества, отнесенный к одному
молю или другой единице массы вещества,
называется критическим удельным объёмом.
Критической принято называть такую
температуру, выше которой газ под
действием давления любого значения не
может быть обращен в жидкость.

На рис. 1. приведена зависимость давления
(упругости насыщенных паров) чистых
веществ от температуры. Эта зависимость
более точно описывает изменение свойств
реальных газов при давлениях до 10 МПа
и температурах от 283 до 293 К, но она не
может численно описывать изменение,
свойств многокомпонентных смесей
месторождений природных газов.

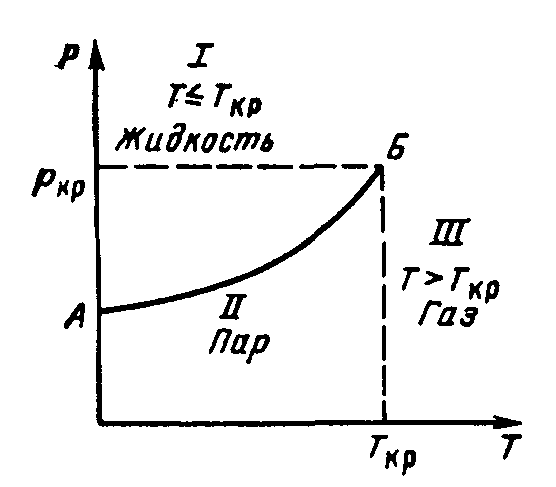
Рисунок
1. Зависимость давления (упругости
насыщенных паров) чистых веществ от
температуры

Давление, необходимое для сжижения газа
при критической температуре, называется
критическим. Кроме критического давления
и критической температуры вводится
понятие критического объёма, равного
объёму одного моля газа при критических
давлении и температуре. Для природных
газов, представляющих собой смесь
отдельных компонентов, значения Р_кр
и Т_кр определяются
как среднекритические (псевдокритические).

Средние критические давление и температуру
смеси можно определить по формулам:

(20)

где х₁, х₂…х_n– объёмные доли компонентов, входящих
в состав газа;

–критические давления компонентов;

– критические температуры компонентов.

Следует отметить, что коэффициент
сверхсжимаемости природной углеводородной
смеси Z_смможно определить по
графической зависимости представленной
на рисунке 1.2.

Если известна относительная плотность
газа
,
то средние критические давление и
температуру природного газа можно
определить по графикам.При содержании в природном газеN₂,
СО₂илиH₂Sв значенияР_кр иТ_крвводятся соответствующие поправки.
Когда содержаниеN₂,CO₂или Н₂Sпревышает 15% об., вместо графиков для
определенияР_криТ_крследует пользоваться формулой (1.20).

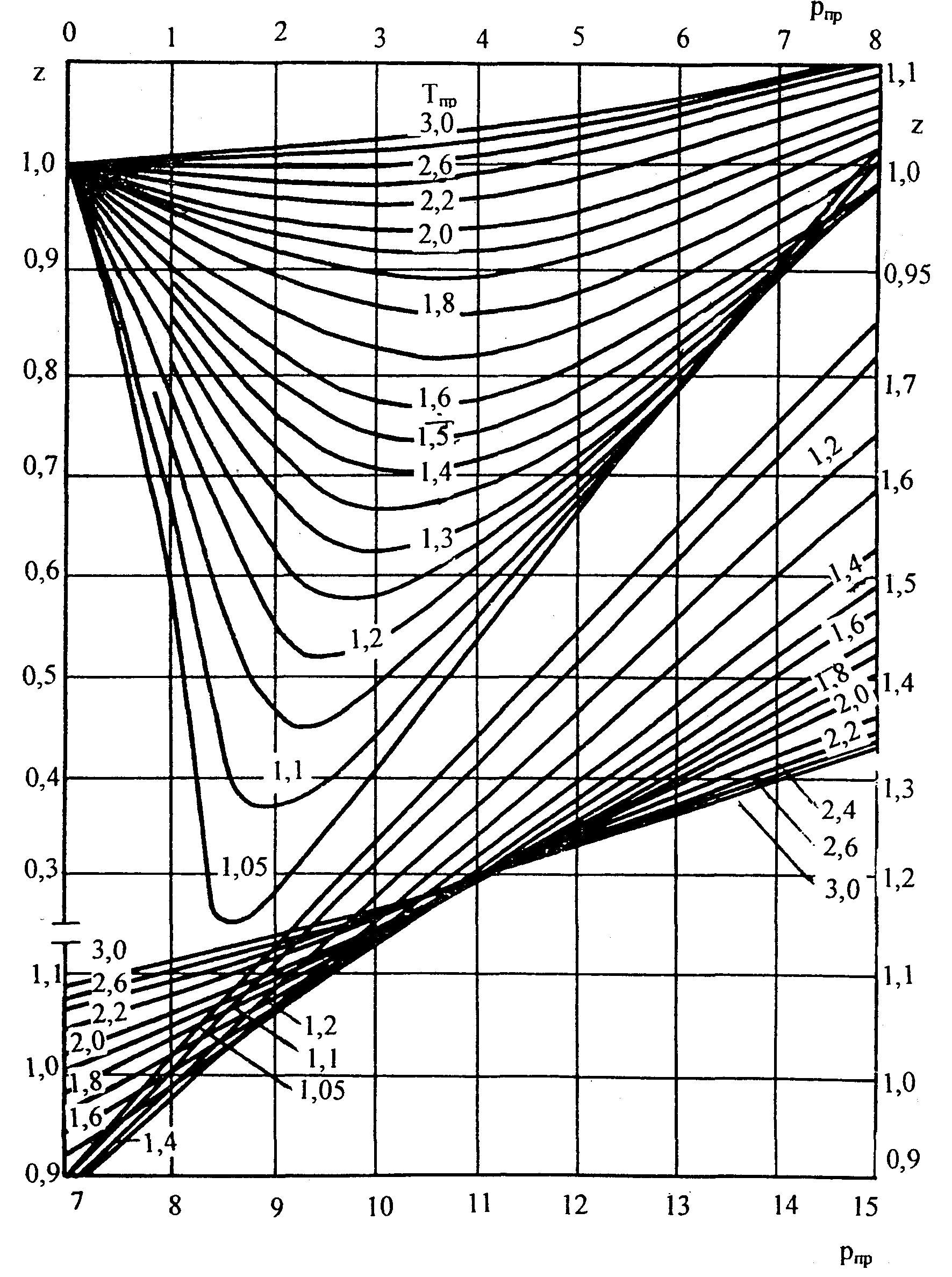
Рис. 1.2. Значение коэффициента
сверхсжимаемости z
по данным Стэндинга и Катца

Для приближенных расчётов при изменении
,
от 0,5 до 0,9 значенияР_криТ_крможно определить
по формулам:

,
МПа (21)

,
К

Часто в расчётах, например, при определении
вязкости и коэффициента сверхсжимаемости
газа, пользуются так называемыми
приведенными давлениями и температурами.
Приведенными параметрами индивидуальных
компонентов называют безразмерные
величины, показывающие, во сколько раз
действительные параметры состояния
газа (давление, абсолютная температура,
объём, плотность, коэффициент отклонения)
больше или меньше критических:

Приведенным давлением Р_прназывается отношение давления газаРк его критическому давлениюР_кр

(22)

Приведенной температурой газа Т_прназывается отношение абсолютной
температуры газаТк его критическому
значению:

,
(23)

Дальнейший прогресс науки и техники
потребовал разработки более точного
уравнения состояния природных газов,
способного правильно описывать изменение
их свойств при давлениях до 100 МПа и
температурах до 573 К в процессах добычи
газа и при давлениях до 20 МПа и низких
температурах до 223 – 93 К (от минус 50 до
минус180°С) в процессах переработки
природных газов.

В решении этой проблемы выявились два
направления:

1) введение поправочного коэффициента
zв уравнение состояния
идеального газа (1.17), учитывающего
отклонение реального газа от идеального,
т. е.pV==zRT

2) дополнение уравнения состояния
идеального газа большим числом констант.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Смесям идеальных газов характерно свойство аддитивности двух показателей: парциального давления и объёма. Другими словами, любому включённому в смесь инертному газу характерно такое поведение, какое было бы, если б он в единственном числе заполнял предлагаемый объём. Для лучшего понимания разумно разобраться, что выражают указанные величины.

Говоря об идеальных газах и их смеси, следует понимать, что изменение условий, например температуры или давления, всё же может спровоцировать химическую реакцию. Важным параметром такой смеси является молярная (весовая) концентрация газового компонента. Данная величина измеряется в мг/м³ и показывает количество конкретного компонента в единице объёма газовой смеси.

Парциальное давление

Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальное давление, создаваемое i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем p_i.

Следует отметить, что равность средней кинетической энергии находящихся в смеси молекул определяет равенство температур всех компонентов термодинамически уравновешенной газовой смеси. Найти общее давление смеси идеальных газов представляется возможным через закон Дальтона, отражаемый аддитивность парциальных давлений, а именно [p=sum p_{i}].

Пользуясь данным законом, найдём давление смеси идеальных газов через следующую формулировку: [p=sum_{i}^{N}=1 rightarrow p_{i}=frac{R T}{V} sum_{i}^{N}=1^{v_{i}}], где N – количество вошедших в смесь газов, v_i– количественный показатель молей i-го газа. Отсюда парциальное давление можно выразить формулой [p_{i}=x_{i} p], где x_i – молярная концентрация i-го газа.

Понятие парциального объёма

Описывая характеристику состояния компонентов идеальной смеси газообразных веществ, парциальный объём, занимаемый i-ым газом в случае удаления других компонентов из сохраняемых условий, является показателем V_i. Аддитивность парциального объёма определяет закон Амага, выраженный формулой [V=sum_{i}^{N}=1 V_{i}].

Зная, что характеризующие состояние смеси инертных газов показатели подчиняются уравнению Менделеева-Клапейрона, выведем формулу:

[p V=frac{m}{mu_{s m}} R T] данное уравнение свои параметры относит ко всей газовой смеси.

[pV=mR_{s m} T] такой вариант уравнения содержит показатель R_sm, обозначающий удельную газовую составляющую смеси.

Уравнение Менделеева-Клапейрона показывает возможность изменения трёх характеризующих состояние идеального газа параметров.

Примеры вычисления парциального давления и объёма

Задача №1

Условие: в сосуде объёмом 2 м³, при постоянной температуре 290 К находится 0,20*10^-3 кг гелия и 1*10^-3 кг водорода. Необходимо вычислить давление смеси и парциальное давление гелия.

Решение.

Сначала вычислим количество молей каждого компонента, используя следующую формулу:

[mathrm{v}{mathrm{i}}=frac{mathrm{m}{mathrm{i}}}{mu_{mathrm{i}}}]

Для расчёта количество молей водорода в смеси нам понадобится его молярная масса, которую возьмём из таблицы Менделеева:

[mu_{mathrm{H}_{2}}=2 * 10^{-3} frac{mathrm{кг}}{text { моль }}]

Теперь можно найти количество молей водорода в смеси:

[mathrm{v}_{mathrm{H}_{2}}=frac{mathrm{m}_{mathrm{H}_{2}}}{mu_{mathrm{H}_{2}}}=frac{1 * 10^{-3}}{2 * 10^{-3}}=0,5 text { (моль) }]

Зная молярную массу гелия из таблицы Менделеева, рассчитаем количество молей гелия в смеси:

[mathrm{v}_{mathrm{He}}=frac{mathrm{m}_{mathrm{He}}}{mu_{mathrm{He}}}=frac{4 * 10^{-3}}{20 * 10^{-3}}=0,2 text { (моль) }]

Теперь можно найти парциальное давление каждого из компонентов с помощью уравнения Менделеева-Клапейрона:

[mathrm{p}_{mathrm{i}} mathrm{V}=mathrm{v}_{mathrm{i}} mathrm{RT}]

Сначала нужно рассчитать давление водорода:

[mathrm{p}_{mathrm{H}_{2}} mathrm{~V}=mathrm{v}_{mathrm{H}_{2}} mathrm{RT} rightarrow mathrm{p}_{mathrm{H}_{2}}=frac{mathrm{v}_{mathrm{H}_{2}} mathrm{RT}}{mathrm{V}}=frac{0,5 * 8,31 * 290}{1}=1205 text { (Па) }]

Рассчитаем парциальное давление гелия:

[mathrm{p}_{mathrm{He}}=frac{mathrm{v}_{mathrm{He}} mathrm{RT}}{mathrm{V}}=frac{0,2 * 8,31 * 290}{1}=482 text { (Па) }]

Теперь найдём полное давление газовой смеси, сложив значения компонентов:

[mathrm{p}=mathrm{p}_{mathrm{H}_{2+}} mathrm{p}_{mathrm{H}}=1205+482=1687 text { Па }]

Ответ: парциальное давление гелия равно 482 Па, а общее давление 1205 Па.

---

Задача №2

Условие: идеальная газовая смесь состоит из 0,5 кг углекислого газа и 0,25 кг кислорода, какой объём они займут, если давление равно 1 атм, а температура смеси равна 300 К?

Решение.

Найдём суммарную массу газовой смеси:

[mathrm{m}=mathrm{m}_{mathrm{O}_{2}}+mathrm{m}_{mathrm{CO}_{2}}=0,5+0,25=0,75 text { (кг) }]

Вычислим массовые компоненты смеси:

[g_{mathrm{O}_{2}}=frac{0,25}{0,75}=0,33] [mathrm{g}_{mathrm{CO}_{2}}=frac{0,5}{0,75}=0,67]

Тогда газовая постоянная смеси равняется:

[mathrm{R}_{mathrm{sm}}=mathrm{R} sum_{mathrm{i}=1}^{mathrm{N}} frac{mathrm{g}_{mathrm{i}}}{mu_{mathrm{i}}}=8,31left(frac{0,33}{32 * 10^{-3}}+frac{0,67}{46 * 10^{-3}}right)=200left(frac{text { Дж }}{text { кгК }}right)]

Пользуясь уравнением Менделеева-Клапейрона, и, зная, что 1 атм равна 10⁵ Па,вычислим объём смеси:

[mathrm{V}_{mathrm{sm}}=frac{mathrm{m}_{mathrm{sm}} mathrm{R}_{mathrm{sm}} mathrm{T}_{mathrm{sm}}}{mathrm{P}_{mathrm{sm}}}=frac{0,75 * 200 * 300}{10^{5}}=0,45left(mathrm{м}^{3}right)]

Ответ: при заданных условиях смесь займёт 0,45 м^3.

Навык определения парциальных давлений и объёма актуален в машиностроении, энергетике и других промышленностях, связанных с использованием тепловых двигателей, приводимых в действие парами высокой температуры.

Уравнение состояния идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:

Уравнение состояния идеального газа

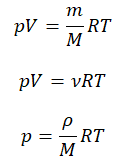
Внимание! При решении задач важно все единицы измерения переводить в СИ.

Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.

Из основного уравнения состояния идеального газа выразим массу:

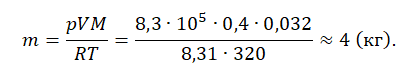
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.

Подсказки к задачам

Важна только та масса, что осталась в сосуде. Поэтому:

Давление возросло на 15%	p2 = 1,15p1
Объем увеличился на 2%	V2 = 1,02V1
Масса увеличилась в 3 раза	m2 = 3m1
Газ нагрелся до 25 о С	T2 = 25 + 273 = 298 (К)
Температура уменьшилась на 15 К (15 о С)	T2 = T1 – 15
Температура уменьшилась в 2 раза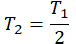
Масса уменьшилась на 20%	m2 = 0,8m1
Выпущено 0,7 начальной массы
Какую массу следует удалить из баллона?	Нужно найти разность начальной и конечной массы:
Газ потерял половину молекул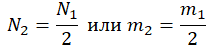
Молекулы двухатомного газа (например, водорода), диссоциируют на атомы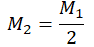
Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ)	M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль
Открытый сосуд	Объем V и атмосферное давление pатм остаются постоянными
Закрытый сосуд	Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины
Нормальные условия	Температура T0 = 273 К Давление p0 = 10 5 Па
Единицы измерения давления	1 атм = 10 5 Па

Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.

2,8 МПа = 2,8∙10 6 Па

1,5 МПа = 1,5∙10 6 Па

Так как половина молекул была выпущена, m₂ = 0,5m₁. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:

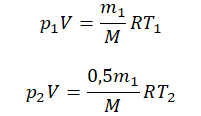
Преобразим уравнения и получим:

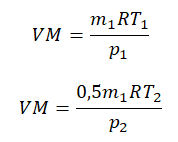
Приравняем правые части и выразим искомую величину:

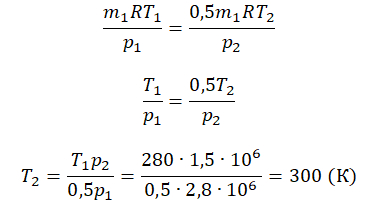
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.

Как найти плотность зная температуру и давление

Комбинированный газовый закон — это формула, которая связывает основные параметры идеального газа и позволяет вычислять неизвестные в случаях, если заданы пять остальных величин.

Идеальный газ

Идеальный газ — это математическая модель с определенными допущениями, которая позволяет исследовать свойства газообразных веществ с достаточной точностью. К допущениям, которые используются в модели идеального газа, относятся:

• пренебрежение размерами молекул;
• силы молекулярного взаимодействия не учитываются;
• соударение атомов и молекул абсолютно упруго;
• газ находится в термодинамическом равновесии.

Благодаря этим допущениям ученые изучили основные свойства газообразных веществ и вывели основные законы, которым подчиняются любые газы. Комбинированный закон объединяет все перечисленные ниже зависимости.

Газовые законы

Любое газообразное вещество характеризуется тремя простыми параметрами: объемом, давлением и температурой. Газ тем и хорош, что он заполняет весь предоставленный объем или может сжиматься до минимальных объемов, иногда переходя в состояние жидкости. Сжимать газ можно двумя способами:

• при постоянном давлении уменьшить температуру;
• при постоянной температуре увеличить давление.

Эти две простые формулировки отражают в себе два известных газовых закона: изобару и изотерму. В изобарном процессе изменение температуры приводит к прямо пропорциональному изменению объема. Вспомните жидкий азот: он занимает минимум места, при этом его температура составляет 63,29 К, что соответствует –209 градусам Цельсия. Если температуру азота поднять до 20 градусов Цельсия, то 1 литр жидкого азота превратится в 700 литров газа. Увеличивается температура, увеличивается объем и наоборот. Эти изменения обусловлены тем, что соотношение объема к температуре газа остается статичным.

В изотермическом процессе температура не изменяется и для сжатия газа придется увеличить давление. Это процесс проще для понимания, так как сдавливая газ мы уменьшаем его объем подобно тому, как утрамбовывание грунта или снега позволяет уложить их более плотно и с меньшим объемом. В этом изотермическом процессе изменение давления приводит к обратно пропорциональному изменению объема. Больше давление, меньше объем и наоборот. Такая динамика обусловлена тем, что произведение давления на объем — это всегда постоянная величина.

Если же объем газа не изменяется, то процесс называется изохорным и в этом процессе отображается взаимосвязь давления и температуры. Согласно закону, изменение одного параметра вызывает прямо пропорциональное изменение другого. Это означает, что увеличение давления в сосуде вызывает рост температуры находящегося там газа. Верно и обратное утверждение.

Комбинированный закон

Все перечисленные законы подчиняются общей формулировке: при постоянстве одного параметра, отношение двух других также постоянно. Обобщая эти законы в динамике получаем комбинированный газовый закон, который описывается формулой:

где P1, V1 и T1 — соответственно начальные давление, объем и температура, а P2, V2 и T2 — конечные.

Используя данную формулу легко определить динамику параметров во время нагрева газа или его сжатия.

Наша программа позволяет рассчитать соотношение параметров идеального газа при их изменении. Для использования калькулятора требуется задать пять известных величин, после чего программа определит последнее неизвестное. Рассмотрим небольшой пример.

Пример использования калькулятора

Представим баллон газа объемом 15 л под давлением 120 кПа и при температуре –20 градусов Цельсия. Определим температуру газа, если баллон будет заменен на емкость объемом 10 л и давлением 150 кПа. На первый взгляд у нас есть все параметры, однако в газовых законах температура обязательно указывается в кельвинах, а не градусах. Для перевода температуры в систему Си достаточно прибавить к значению величину 273. Получаем, что температура газа составляет 253 К. Теперь вводим данные в соответствующие ячейки и смотрим на результат: конечная температура теперь равна 210 К или –63 градуса Цельсия. Очевидно, что газ подчинился приведенным выше законам и при уменьшении объема его температура также уменьшилась.

Заключение

Газовые законы — серьезная тема школьного курса физики, которую более подробно разбирают на первом году обучения в вузах. Комбинированный закон газа прост на первый взгляд, но обилие параметров может запутать школьника, а выведение пропорций и вовсе способно превратить задачу в ад. Для упрощения расчетов используйте наш онлайн-калькулятор, не забывая переводить все заданные параметры в систему СИ.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:

Примеры задач на уравнение Менделеева-Клапейрона

В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?

Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)

В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Теперь немного формул.

где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль

Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также

где n — число молей газа

И как нетрудно заметить, соотношение

есть величина постоянная для одного и того же количества моль газа.

И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.

Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.

Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры

Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры

Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.

Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.

Введение

Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].

Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.
Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.

К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.

В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.

Математическая модель определения плотности газа

Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:

1. Уравнение Менделеева-Клапейрона:

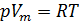(1),

— давление газа;

— молярный объём;

R — универсальная газовая постоянная,

;

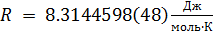T — абсолютная температура, T=273.16 К.

2. Два измеряемых параметра:

p – давление газа, Па
t – температура газа, °С.

Известно, что молярный объём зависит от объёма газа V и количества молей газа 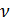в этом объёме:

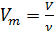(2)

Также известно, что

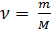(3),

где: m – масса газа, M – молярная масса газа.

Учитывая (2) и (3) перепишем (1) в виде:

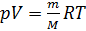(4).

Как известно, плотность вещества

равна:

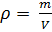(5).

Из (4) и (5) выведем уравнение для плотности газа

:

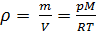(6)

и введём обозначение параметра

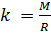, который зависит от молярной массы газовой смеси:

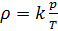(7).

Если состав газовой смеси не меняется, то параметр k является константой.
Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.

Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.

Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:

• 23 % по весу из молекул кислорода
• 76 % по весу из молекул азота
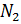
• 1 % по весу из атомов аргона

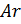
Молярные массы этих веществ воздуха будут соответственно равны:

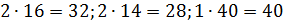, г/моль.

Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:

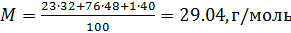
Теперь, зная значение константы

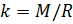, мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений

и t:

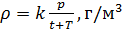
Приведение плотности газа к нормальным, стандартным условиям

Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].

Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.

Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.

Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.

Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура 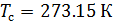и абсолютное давление :

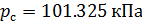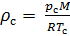(9).

Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для :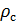

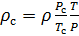(10).

Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура 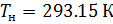и абсолютное давление

:

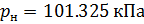(11).

В уравнениях (10) и (11) используем значения параметров воздуха , T и P из уравнения (8), полученные в рабочих условиях.

Реализация измерительного канала давления и температуры

Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.

Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).

Для этого, на аппаратном уровне, нам понадобятся компоненты:

1. Arduino (Uno, …) – используем как программатор;
2. микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
3. кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
4. тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
5. BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
6. преобразователь интерфейсов TTL/USB;
7. расходные материалы – провода, припой, монтажная плата, и др.

Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.

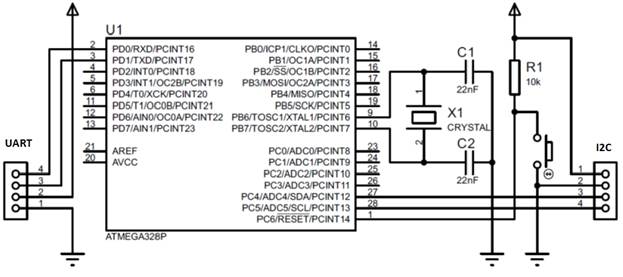
Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры

Теперь рассмотрим этапы осуществления нашей задачи.

1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.

2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.

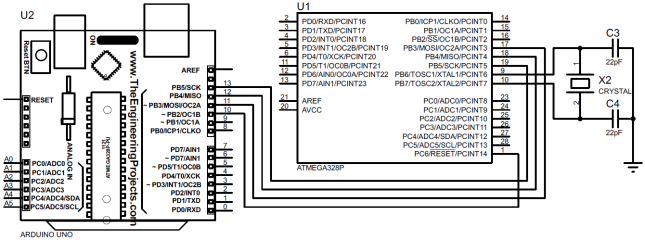
Рис. 2 – Схема подключения микроконтроллера к программатору

3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.

Рис. 3 Система измерения давления и температуры

Программа Python для фильтрации по каналам температуры и давления, и получение результатов

Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.

Результаты расчёта представлены листингом и рис. 4, 5, 6.

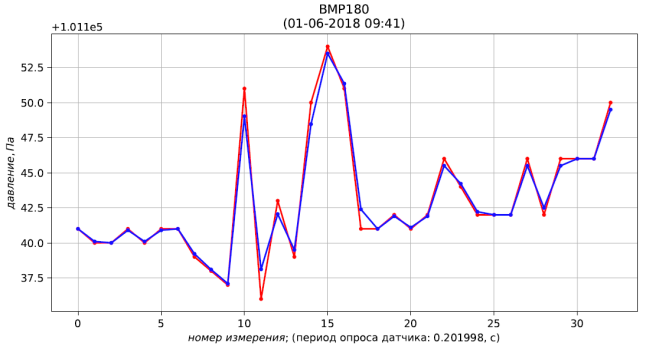
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления

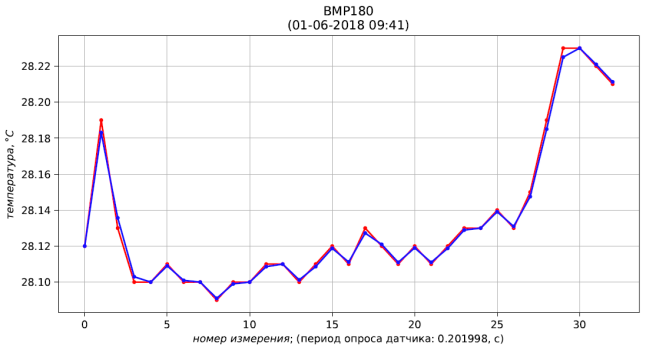
Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры


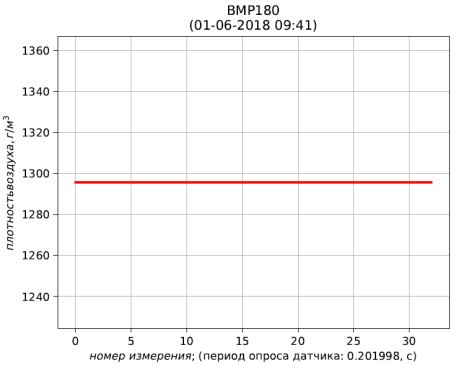
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)

Выводы

Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.

Уравнение состояния идеального газа. Газовые законы.

Уравнение состояния идеального газа

(уравнение Менделеева – Клапейрона).

Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние.

В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеаль­ного газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул.

В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m.

Мы знаем, что 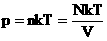. Следовательно, 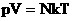. Учитывая, что 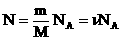, получим: .

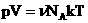Произведение постоянных величин есть величина постоянная, следовательно: 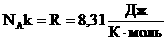– универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая).

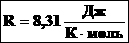
Таким образом, имеем:

– уравнение состояния (уравнение Менделеева – Клапейрона).

Другие формы записи уравнения состояния идеального газа.

1.Уравнение для 1 моля вещества.

Если n=1 моль, то, обозначив объем одного моля V_м, получим: .

Для нормальных условий получим:

2. Запись уравнения через плотность: – плотность зависит от температуры и давления!

3. Уравнение Клапейрона.

Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда:

Эта запись означает, что для данной массы данного газа справедливо равенство:

Для постоянной массы идеального газа отношение произве­дения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: .

Газовые законы.

1. Закон Авогадро.

В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов).

Доказательство:

Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково.

2. Закон Дальтона.

Давление смеси газов равно сумме парциальных (частных) давлений каждого газа.

Доказательство:

3. Закон Паскаля.

Давление, производимое на жидкость или газ, передается во все стороны без изменения.

[spoiler title=”источники:”]

http://planshet-info.ru/kompjutery/kak-najti-plotnost-znaja-temperaturu-i-davlenie

http://www.eduspb.com/node/1742

[/spoiler]

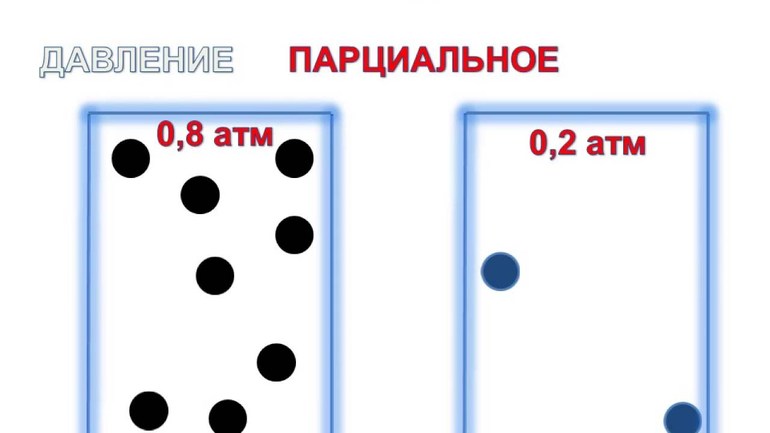
Трактовка закона

Учёный Дальтон в 1801 году сформировал закон парциальных давлений: Па смеси из идеальных газов равняется сумме рi её компонентов. Уравнение имеет следующий вид: Рсм=n (сумма pi), где n — число долей смеси.

Для определения парциального давления в химии используется отдельный компонент из атмосферного воздуха. При расчете учитывается значение каждого отдельного вещества, их число, температуры с объёмами. При необходимости можно найти общий показатель, сложив давление каждого компонента в отдельности.

Каждый газ в сосуде должен обозначаться как «идеальный». При нормальных условиях они взаимодействуют с углекислым газом, водородом, водой, азотом, водяным паром, кислородом, компонентами крови и прочими компонентами из таблицы Менделеева. При этом не образуются соединения. Отдельные молекулы способны сталкиваться между собой, отталкиваясь, но не деформируясь.

Физические и химические задачи решаются с помощью формулы парциального давления (закон открыли учёные Бойль и Мариотт): (k = P x V). Кроме полного варианта, уравнение записывается сокращённо k = PV, где:

• k равно постоянной величине;
• Р — давление;
• V — объем.

Второстепенные значения

Давление может измеряться в разных величинах: процент, паскаль (Па). Смысл последнего: сила в 1 ньютон приложена к площади в 1 кв. м. Если результат такой зависимости записывается в атмосферах, тогда для его нахождения потребуется учесть, что одна атмосфера равняется 101,325 Па.

Температура идеального газа повышается, если увеличивается объём, а снижается, если уменьшается последний показатель. Такое соотношение может называться законом Чарльза, который имеет следующий математический вид: k = V / T. Значение температуры в уравнении измеряется в градусах Кельвина. Оно зависит от градусов Цельсия. Чтобы его найти, прибавляется 273.

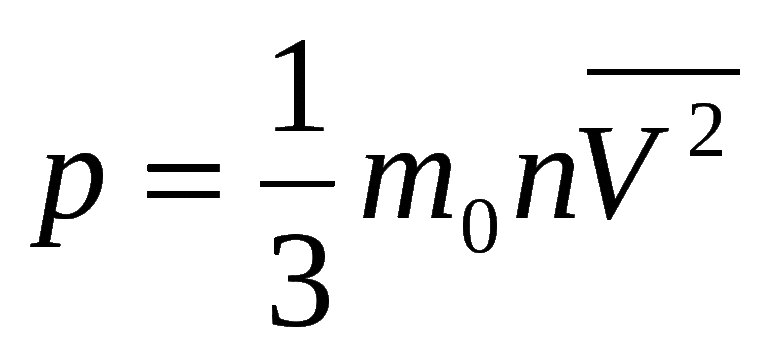
Уравнение используется в химии для определения мольной доли (концентрация, которая выражается через отношение количества молей 1 компонента к суммарному числу молей пары веществ, входящих в смесь). Кроме объёма, для газа характерна молярная масса (вес одной доли компонента) и объём. Существуют легкие способы её подсчёта:

1. Стандартная. Измеряется в граммах и килограммах.
2. Молекулярная. Так как газы весят мало, их вес вычисляется в специальной единице измерения — молярная масса. Для её определения суммируется вес составных атомов. Каждый компонент сравнивается с массой карбона, равной 12.

Уравнения Дальтона и Бойля

Физик и химик Дальтон считается первым учёным, предположившим структуру атомных элементов, их свойства. Общее давление вычисляется следующим образом: Р= P1 + P2 + P3. Пример: в колбе содержится по 10 г оксигена и нитрогена. Их общее Р будет равно 20 (10+10). Для вычисления pi используется температура, равная 37 градусам Цельсия.

Чтобы перевести её в градусы Кельвина, значение по Цельсию, равное 37, добавляется к 273. Результат — 310. Для вычисления количества молей газов используется масса, поделённая на молярную. Если уравнение касается нитрогена, вес каждого компонента соответствует цифре 14.

Так как вещество содержит в себе 2 атома, то 14х2, что равно 28. Масса в граммах делится на полученный результат. Таким способом вычисляется количество молей, приблизительно равное 0,4 моль. Чтобы найти аналогичное значение у оксигена, применяется масса 16. Вещество относится к двухатомным газам, поэтому 16х2 равняется 32. По результатам получается, что 0,3 моль оксигена содержится в составе газовой смеси.

Если в задаче указывается общее давление и pi в атмосферах, тогда используется в качестве константы R (0.0821 л атм/K моль). При подстановке данных в уравнение можно узнать Pобщее. Чтобы вычислить ПД нитрогена, 0,4 моль умножается на константу и температуру. Результат делится на 2 литра, что приблизительно равно 5.09 атм. Аналогичные шаги выполняются для вычисления ПД оксигена. Конечный результат равен 3.82 атм.

Свойства веществ

Значение pi газа, растворённого в жидкости, равняется pi того вещества, который образовался бы в фазе газообразования в случае равновесия с жидкостью при аналогичной температуре. Парциальное давление (ПД) измеряется в качестве термодинамической активности молекул вещества.

Газы постоянно вытекают из сферы с высоким ПД в область с низким давлением. Чем больше такая разница, тем быстрее поток. Газам свойственно растворяться, диффундировать, реагировать на ПД. В некоторых случаях показатель не зависит от концентрации газовой смеси.

При решении задач в области химии и физики учитываются свойства газов: сжимаемость и способность расширяться. Они не имеют своей формы, поэтому расширяются до заполнения сосуда, принимая его форму. По аналогичной причине они не имеют объёма. Газ давит на стенки ёмкости по всем направлениям одинаково. Характерное свойство компонентов — способность смешиваться между собой в разных соотношениях.

Так как объём зависит от температуры и давления, поэтому в норме должно быть 0 °C и 760 мм рт. ст. При этом нет места влаги. Если объём считается нормальным, его обозначают стоящей впереди буквой. Подобная зависимость отображается в термодинамике с помощью графика. Если доказана зависимость объема от давления, при этом температура постоянная, используются изотермы (линии, которые изображают на диаграмме процесс с неизменной температурой).

Точки и функции

В законе Бойля чётко указана зависимость объёма от давления при одинаковой температуре. Если данные нанести на график в функцию давления, через точки можно будет провести кривую. Точный эксперимент и незначительный разброс точек позволяют описать объёмное поведение системы с небольшой погрешностью.

Несколько подобных кривых для разных температур во всём диапазоне изученных условий позволяет описать объёмное поведение газа. Одновременно отображаются кривые постоянного давления, которые описывают изменения основных показателей. Чтобы получить окончательные результаты, кривые требуют незначительного сглаживания. Подобные графики сделать самостоятельно менее сложно.

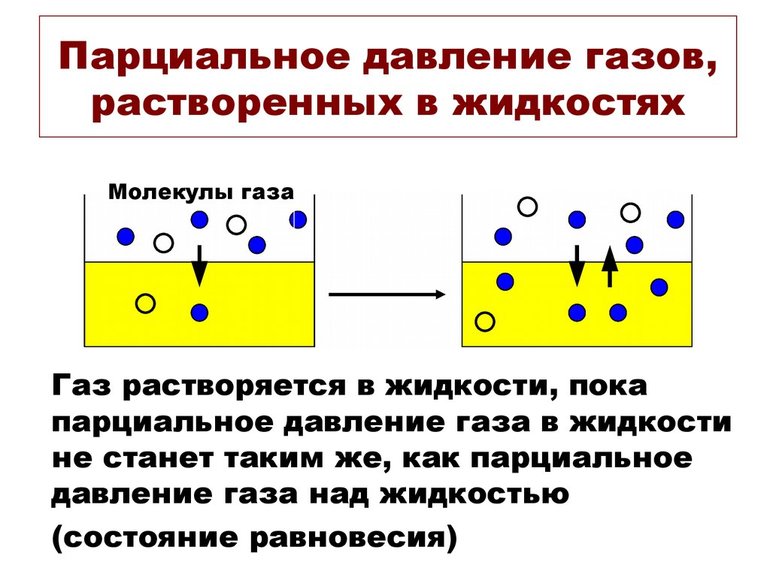
Объём газа при неизменной температуре сильно изменяется с колебаниями давления. Но графически представить такую зависимость в широком диапазоне изменения давлений трудно. Если охвачена широкая область изменения, используются крупные масштабы.

Для упрощения процесса построения на график наносится зависимость произведения Р от давления при одной температуре, что существенно уменьшает область выявления функции. Наибольший эффект получается от применения 1−2 специальных функций объёма, которые называются коэффициентом сжимаемости и остаточным объёмом.

Каждое понятие характеризуется объёмным поведением газа с учётом его отклонений от нормального состояния вещества и созданных идеальных условий. Чтобы упростить поставленную задачу, график отображается на специальной бумаге либо при помощи компьютерных программ. Во втором случае достаточно ввести данные. Сервис самостоятельно строит прямые, кривые и прочие элементы графика.

Простые зависимости лучше отображать в стандартных программах Word. Графические сложные задачи в химии и физике решаются с помощью «Agrafer» — известная компьютерная программа, которая используется не только студентами, но и школьниками.