М.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи на газовые
законы
 Графические
Графические
задачи заслуживают особого внимания, ибо, как
показывает опыт, они представляют наибольшую
трудность для абитуриентов. Причина проста:
этому типу задач в школьном курсе уделяют
неоправданно мало внимания – решают одну-две
задачи, притом формально, не вникая в суть. Кроме
того, в школе ограничиваются изопроцессами,
когда масса газа постоянна. Именно поэтому на
вступительных экзаменах абитуриенты теряются и
не знают даже, с чего начать и каковы методы
решения.
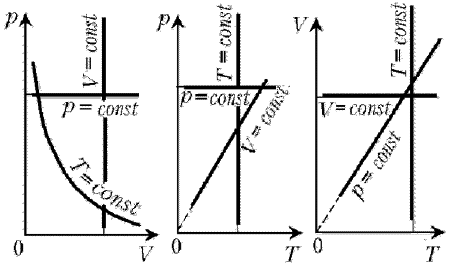
Напомним, как изображаются на диаграммах
изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических
задач. В задачах первого типа графически
задается какой-то изопроцесс в явной или неявной
форме. Для решения таких задач можно предложить
следующий «план действий»:
1. Установить характер изображенного процесса
(если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из
изопроцессов и изобразить его графически
(провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с
линией (или с линиями) представленного процесса
(или процессов).
4. Спроецировать точку (или точки) пересечений
этих линий на одну из координатных осей (выбор
оси произволен).
5. Рассмотреть состояния данной массы газа,
которым соответствуют эти проекции, и, используя
известные газовые законы, ответить на
поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
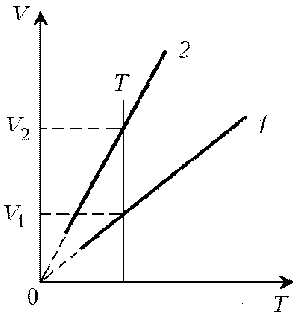 Пример
Пример
1. Какая из двух линий графика соответствует
большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за
линии. Эти линии выражают прямо пропорциональную
зависимость между объемом газа и его
температурой, а это возможно для идеального газа
только при изобарическом процессе,
следовательно, изображенные линии графика –
изобары.
Проведем изотерму до пересечения с обеими
изобарами, а точки их пересечения спроецируем на
ось ординат (объемов). Из построения видно, что V2
> V1. Поскольку при изотермическом
процессе газ подчиняется закону Бойля–Мариотта:
р1V1 = р2V2, то р1 > р2.
Напомним, что все точки, лежащие на одной изобаре,
соответствуют состояниям с одинаковым
давлением.
Читателю предоставляется возможность решить
эту задачу путем построения изохоры и
проецирования точек пересечения на ось
температур (еще раз стоит напомнить, что выбор
способа решения в задачах данного типа
произволен).
 Пример
Пример
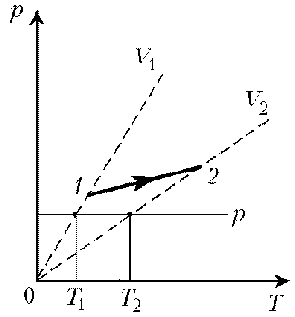
2. При нагревании идеального газа постоянной
массы получена зависимость р(T) при переходе из
состояния 1 в состояние 2. Как при этом переходе
менялась плотность газа?
Решение. Прежде всего обратим внимание на то,
что линия графика не описывается ни одним из
изопроцессов («неявная форма»).
Проведем через начальную и конечную точки
линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму)
и, спроецировав точки ее пересечения с изохорами
на ось Т, убедимся, что Т2 > Т1. При
изобарическом процессе, по закону Гей-Люссака, V ~
T, следовательно, V2 > V1. А т.к.
плотность и объем связаны обратной зависимостью
(при данной массе), то r1 > r2, откуда следует, что газ
расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий
цикл, совокупность процессов, в результате
которых данная масса газа возвращается в
исходное состояние. Этот цикл может быть задан на
разнообразных диаграммах: p, V; p, T; V, T и др. Как
правило, в таких задачах требуется представить
заданный цикл на других диаграммах. Эти задачи
важны при рассмотрении первого закона
термодинамики, когда совершается
макроскопическая работа и происходит процесс
теплообмена. Важно понимать, что цикл – это
замкнутый процесс, и он должен быть замкнутым на
любой диаграмме!
При решении предлагается следовать следующему
алгоритму:
1. Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между
собой величины).
4. По графику выяснить, как меняется каждая
величина.
Условимся для удобства обозначать ход процесса
стрелками: – увеличение величины, Ї –
уменьшение величины.
 Пример
Пример
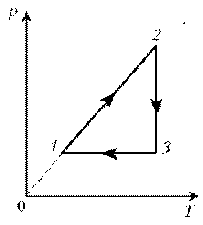
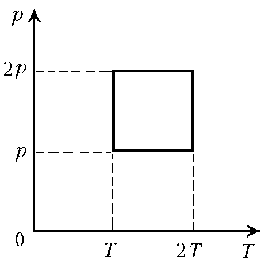
3. На диаграмме р, T изображен цикл идеального газа
постоянной массы. Изобразите его на диаграмме р,
V.
Решение. Проведем поэтапный анализ
представленного цикла:
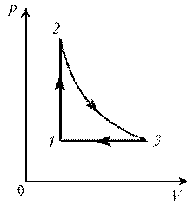 1–2:
1–2:
изохорический процесс; закон Шарля; р ~ T; р, T.
2–3: изотермический процесс; закон
Бойля–Мариотта; р ~ 1/V; рЇ; V
3–1: изобарический процесс; закон Гей-Люссака; V ~
T; TЇ; VЇ.
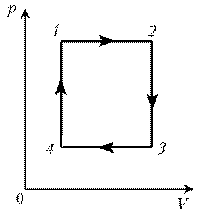
Теперь результаты поэтапного анализа
перенесем на диаграмму р, V.
 Пример
Пример
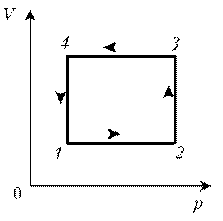
4. Для постоянной массы идеального газа
представлен цикл на диаграмме р, V. Изобразить
этот цикл на диаграмме V, T.
Решение. Проведем поэтапный анализ:
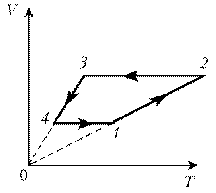 1–2:
1–2:
изобарический процесс; закон Гей-Люссака; V~ T; V; T.
2–3: изохорический процесс; закон Шарля; р~ T; рЇ; TЇ.
3–4: изобарический процесс; закон Гей-Люссака; V ~
T; VЇ; TЇ.
4–1: изохорический процесс; закон Шарля; р ~ T; р; T.
 Пример
Пример
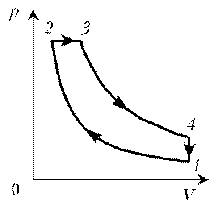
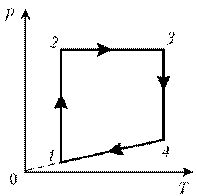
5. Изобразите на диаграмме р, Т цикл постоянной
массы идеального газа, представленный на
диаграмме р, V.
Решение
1–2: изотермический процесс; закон
Бойля–Мариотта; р ~ 1/V; р; VЇ
 2–3:
2–3:
изобарический процесс; закон Гей-Люссака; V~T; V; T
3–4: изотермический процесс; закон
Бойля–Мариотта; р ~ 1/V; рЇ; V
4–1: изохорический процесс; закон Шарля; р ~ T; рЇ; TЇ.
А вот блок задач с необычной постановкой
условия. Впрочем, и они решаются достаточно
стандартными методами, а известные формулы
начинают играть новыми красками. Давайте
убедимся в этом.
 Пример
Пример
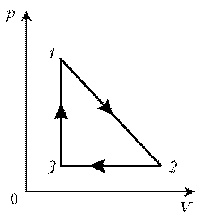
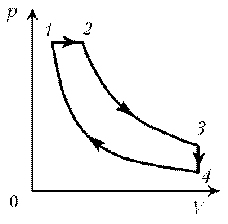
6. Как менялась температура постоянной
идеального массы газа на протяжении цикла? Точки
1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные
точки 1, 2, 3 и касательную к участку 1–2. Как
следует из теории, изотермы, более удаленные от
координатных осей, соответствуют более высоким
температурам. В этом можно убедиться, используя
методы, предложенные в предыдущих задачах.
Проходим по циклу:
 1–1*:
1–1*:
переход на более «высокую» изотерму, значит,
температура растет.
1*–2: переход на более «низкую» изотерму,
следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это
означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму,
значит, температура повышается.
Как видим, ничего необычного в этой задаче нет,
при решении использованы известные факты.
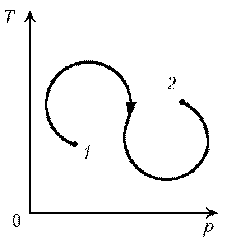 Пример
Пример
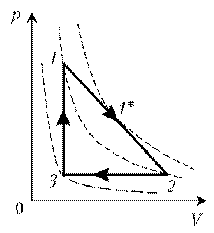
7. Как менялась плотность идеального газа
постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные
точки 1, А, В, 2. Проведем изотерму, пересекающую
все изохоры, и спроецируем эти точки пересечения
на ось р. Плотность r = m/V, т.е. плотность обратно
пропорциональна объему. При 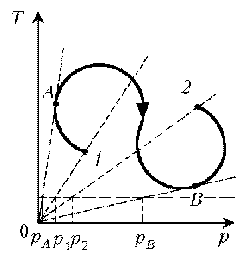 изотермическом
изотермическом
процессе р ~ 1/V. Таким образом, задача сводится к
вопросу, каким изохорам соответствуют большие
или меньшие объемы. Обратимся к графику:
1–А: р1 > рA Ю V1
< VA Ю r1
> rА Ю rЇ.
А–В: рВ > рА Ю VВ
< VА Ю rВ
> rА Ю r
В–2: рВ > р2 Ю VВ
< V2 Ю rВ
> r2 Ю rЇ
Итак, сначала плотность уменьшается, затем
увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют»
формулы, позволяющие получить ответ, казалось бы,
без конкретных данных.
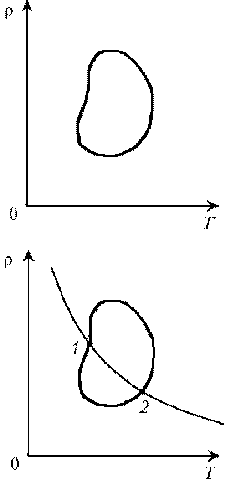 Пример
Пример
8. Дан цикл идеального газa постоянной массы.
Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в
виде уравнения Клапейрона–Менделеева! Применим
его для двух произвольных состояний, учитывая,
что в этих состояниях, по условию, давления
одинаковы. Выразим объем через массу и плотность:
V = m/r. Тогда:
р1V1 = р1m/r1
= nRT1;
р2V2 = p2 m/r2
= nRT2.
Теперь остается разделить одно уравнение на
другое:
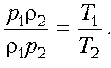
Но р1 = р2, значит, r1T1
= r2T2, или rT
= const, или r ~ 1/T.
Как известно, обратно пропорциональная
зависимость изображается гиперболой. Точки ее
пересечения с циклом и будут соответствовать
состояниям с одинаковым давлением. Заметим:
любые другие гиперболы, пересекаясь с линией
графика, будут давать пары состояний с
одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о
которых говорилось выше, – задачи, в которых
масса газа меняется. К сожалению, как правило,
подобные задачи в школьном курсе не
рассматриваются. Это и приводит к неприятностям
на вступительных экзаменах: срабатывает «фактор
неожиданности», и абитуриент теряется…
 Пример
Пример
9. Идеальный газ с молярной массой М участвует в
изотермическом процессе. При этом получена
зависимость между объемом V и давлением р.
Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева:
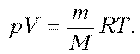
 По
По
условию, T, M и R – постоянные, следовательно, m ~ рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m ~ р; р; m
2–3: T = const, р = const; m ~ V; V; m
3–4: T = const, V = const; m ~ р; pЇ; mЇ
4–1: T = const, р = const; m ~ V; VЇ; mЇ
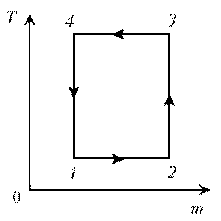 Пример
Пример
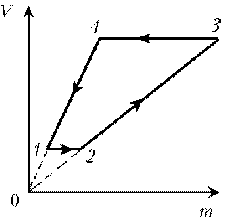
10. Идеальный газ с молярной массой М совершает
изобарический процесс, что отражено на
представленной диаграмме T, m. Изобразите этот
цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева: 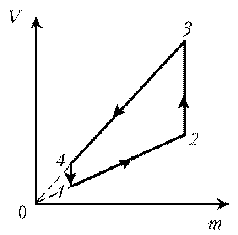
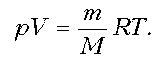
1–2: р = const; T = const; V ~ m; m; V.
2–3: р = const; m = const; V ~ T; T; V.
3–4: р = const; T = const; V ~ m; mЇ; VЇ
4–1: р = const; m = const; V ~ T; TЇ; VЇ.
Легко видеть, что ничего «необычного» в этих
задачах нет, они решаются все теми же методами,
которые рассматривались выше. Хочется надеяться,
что после знакомства с ними у школьников и
абитуриентов проблем уже не будет.
 Пример
Пример
11. Дан график зависимости р(V) для процессов,
проводимых с идеальным газом неизменного
химического состава при постоянной температуре.
Кривые 2–3 и 4–1 – гиперболы. Изобразите эти
процессы в координатах m, р.
Решение. Запишем уравнение
Клапейрона–Менделеева: . 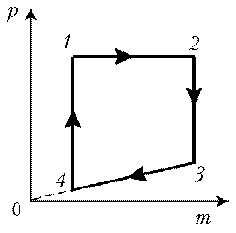
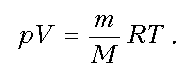
1–2: T = const, р = const; V ~ m; V; m
2–3: T = const, р ~ 1/V; m = const; рЇ
3–4: T = const, V = const; р ~ m; pЇ; mЇ
4–1: T = const, р ~ 1/V; m = const; р
Задачи для самостоятельного решения
- 1. Изобразите цикл постоянной массы идеального
газа на диаграммах V, T; р, V.
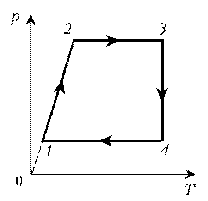
- 2. Изобразите цикл постоянной массы идеального
газа на диаграммах р, T; р, V.
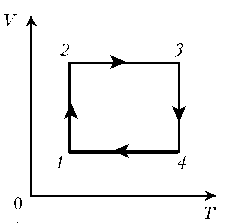
- 3. Как менялась плотность постоянной массы
идеального газа при переходе 1–2?
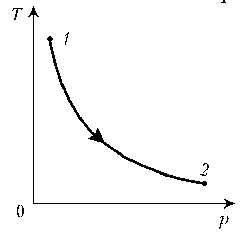
- 4. Изобразите цикл постоянной массы идеального
газа на диаграммах р, V и р, T.
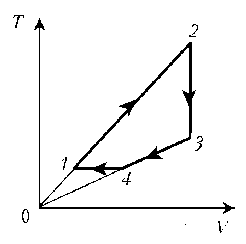
- 5. Идеальный газ постоянной массы расширяется по
закону рV2 = const. Как при этом меняется
температура газа: повышается или понижается?
- 6. Как менялась температура постоянной массы
газа при переходе 1–2?
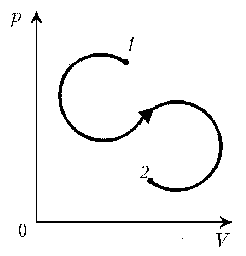
- 7. Дан цикл постоянной массы идеального газа.
Указать на линии графика состояния, которым
соответствуют экстремальные значения
температуры.
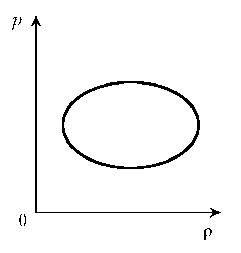
- 8. Над постоянной массой идеального газа
совершается работа по представленному циклу.
Найти отношение экстремальных значений объема в
цикле и изобразить цикл на диаграммах р, V; V, T.
Вопросы: Состав и физико-химические
свойства природных газов, их классификация.
Газовые смеси, плотность газов, состав
газовой смеси. Парциальные давление и
объём в смеси идеальных газов. Аналитические
методы расчета физических свойств
природных газов. Вязкость газа
Состав и физико-химические свойства природных газов. Классификация природных газов
Природные газы, добываемые из чисто
газовых, нефтяных и газоконденсатных
месторождений, состоят из углеводородов
гомологического ряда метана (СnН2n+2), а также неуглеводородных
компонентов: азота (N2),
углекислого газа (СО2), сероводорода
(H2S),
редкоземельных (инертных) газов (гелия,
аргона, криптона, ксенона), ртути. Число
углеродных атомов n в молекуле углеводородов
может достигать 17 и более.
Метан
(СН4),
этан (С2Н6)
и этилен (С2Н4)
при нормальных условиях (Р = 0,1 МПа и T =
273 К) являются реальными газами. Пропан
(С3Н8),
пропилен (С3Н6),
изобутан (i-C4H10),
нормальный бутан (n-С4Н10),
бутилены C4Н8)
при атмосферных условиях находятся в
парообразном (газообразном) состоянии,
при повышенных давлениях – в жидком. Они
входят в состав жидких (сжижаемых,
сжиженных) углеводородных газов.
Углеводороды, начиная с изопентана
(i-C5H12)
и более тяжелые (17 > n > 5) при атмосферных
условиях находятся в жидком состоянии.
Они входят в состав бензиновой фракции.
Углеводороды, молекула которых состоит
из 18 и более атомов углерода (отC18H38),
расположенных в одну цепочку, при
атмосферных условиях находятся в твердом
состоянии.
Природные газы подразделяются на три
группы:
1. Сухой газ, свободный от тяжелых
углеводородов, добываемый из чисто
газовых месторождений.
2. Смесь сухого газа, пропанобутановой
фракции (сжиженного газа) и газового
бензина, добываемые вместе с нефтью.
3. Сухой газ и жидкий углеводородный
конденсат, добываемые из газоконденсатных
месторождений.
Углеводородный конденсат состоит из
большого числа тяжелых углеводородов,
из которых можно выделить бензиновые,
лигроиновые, керосиновые, а иногда и
более тяжелые маслянистые фракции.
Следует отметить, что в промышленности
используются искусственные газы,
полученные из твердых топлив (горючие
сланцы, бурый уголь и пр.).
Газовые смеси. Плотность газов
Под плотностью, или объёмной массой,
тела понимают отношение массы тела в
состоянии покоя к его объёму.
Плотность газа
![]() в нормальных физических условиях (при
в нормальных физических условиях (при
0,1013 МПа и 273 К) можно определить по формуле
![]() (1)
(1)
где М –молекулярная масса.
Если плотность газа задана при давлении
0,1013 МПа, то пересчёт её на другое давление
(при той же температуре) для идеального
газа проводится по формуле
![]() (2)
(2)
где Р – давление, МПа.
Часто для характеристики газа применяют
относительную плотность его по воздуху
при нормальных условиях (0,1013 МПа и 273 К)
![]() (3)
(3)
Коммерческие расчёты в газовой
промышленности проводят при стандартных
физических условиях – 0,1013 МПа и 293 К.
Состав газовой смеси
Газовые смеси (как и смеси жидкостей и
паров) характеризуются массовыми или
молярными концентрациями компонентов.
Объёмный состав газовой смеси примерно
совпадает с молярным, так как объёмы 1
кмоля идеальных газов при одинаковых
физических условиях по закону Авогадро
имеют одно и то же численное значение,
в частности при 273 К и 0,1013 МПа составляют
22,41 м3.
Для характеристики газовой смеси следует
знать её среднюю молекулярную массу,
среднюю плотность (в кг/м3) или
относительную плотность по воздуху.
Если известен молярный состав смеси в
процентах, то среднюю молекулярную
массу вычисляют по формуле
![]() (4)
(4)
где у1, у2, …,уn—молярные
(объёмные) доли компонентов, %;
Ml,
М2, …, Mn– молекулярные массы
компонентов.
Если
задан массовый состав смеси, то её
среднюю молекулярную массу определяют
по формуле
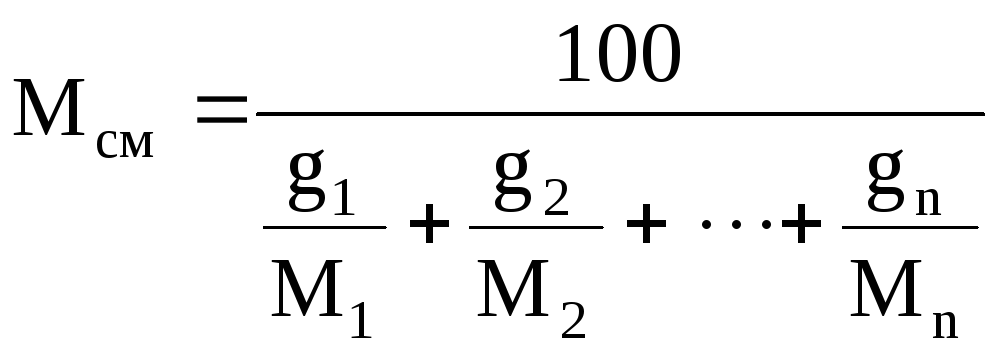 (5)
(5)
где g1,g2,
…,gn—массовые
доли компонентов, %.
Плотность смеси ρсм определяется
по вычисленному значению средней
молекулярной массы Мсмпо формуле,
аналогичной (1)
![]() (6)
(6)
Относительную
плотность смеси вычисляют по формуле
![]() (7)
(7)
где ρcми ρв— плотности соответственно смеси и
воздуха при 273 К и 0,1013 МПа.
Парциальные
давление и объём компонента в смеси
идеальных газов
Смеси
идеальных газов характеризуются
аддитивностью
парциальных давлений и парциальных
объёмов. Это означает, что каждый газ в
смеси идеальных ведет себя так, как если
бы в данном объёме он был бы один.
Парциальное давление газа – давление
газа, входящего в состав газовой смеси,
которое он оказывал бы, занимая один
весь объём смеси и находясь при неизменных
первоначальных объёме и температуре.
Парциальный объём – объём, который
занимал бы газ, входящий в состав газовой
смеси, если бы он находился при тех же
давлении и температуре, что и вся смесь.
Аддитивность
парциальных давлений выражается законом
Дальтона, согласно которому
![]() (8)
(8)
где р – общее давление смеси
газов;
pi –парциальное давление
i-го компонента в смеси;
![]() (9)
(9)
или
![]() (10)
(10)
где ni
– число молей i-го компонента в смеси;
N – общее число молей смеси;
уi –
ni/N–молярная доля i-го компонента в
смеси.
Таким образом, парциальное давление
компонента рiв смеси
идеальных газов равно произведению его
молярной доли в смесиyiна общее давление смеси газовр.
Аддитивность парциальных объёмов
компонентов газовой смеси выражается
законом Амага, согласно которому
![]() (11)
(11)
где V– общий объём смеси;
Vi, – парциальный объём
i-го компонента в смеси.
![]() (12)
(12)
или
![]()
![]() (13)
(13)
Таким образом, парциальный объём
компонента в смеси идеальных газов; Vi
–равен произведению его
молярной долиуi в
смеси на общий объёмVсмеси газов.
Аналитические
методы расчета физических свойств
природных газов
Для определения многих физических
свойств природных газов используют
уравнение состояния – аналитическую
зависимость между параметрами,
описывающими изменение
простого или сложного вещества (давление,
объём и температура).
Клапейрон и Менделеев предложили
следующее уравнение состояния идеальных
газов:
![]() (14)
(14)
где р – абсолютное давление. Па;
V –объём, м3;
G– масса вещества, кг;
Т– абсолютная температура, К;
R – удельная
газовая постоянная, Дж/(кг К).
Идеальным называется газ, собственный
объём молекул, которого пренебрежимо
мал по сравнению с объёмом, занимаемым
газом, и когда отсутствует взаимодействие
между молекулами.
С термодинамической точки зрения
идеальным называется газ, для которого
справедливо равенство
![]() (15)
(15)
где Е – внутренняя энергия парообразования,
Дж/моль или
![]() (16)
(16)
где z – коэффициент
отклонения реального газа от закона
идеального.
Экспериментальная проверка уравнения
(14), проведенная многими исследователями,
показала, что изменение свойств реальных
газов при высоких давлениях нельзя
описать зависимостью (16).
Голландский физик Ван-дер-Ваальс в 1879
г. предложил учесть собственный объём
молекул газа и силы их взаимного
притяжения посредством введения
дополнительных членов в уравнение
Клапейрона – Менделеева:
![]() (17)
(17)
где v – V/G– удельный объем газа, м3/кг;
а/v2– константа сцепления
молекул. Па;
b– поправка на собственный объём
молекул, м3.
В уравнении (17) слагаемое а/v2,выражает внутреннее давление, которое
является как бы равнодействующей сил
притяжения всех молекул в объёмеV.Оно прибавляется к внешнему давлению.
Это уравнение приближенное.
В соотношениях для критического состояния
вещества
 (18)
(18)
коэффициенты aиbвыражаются
через критическое давлениеркри критическую температуруТкр
следующим образом:
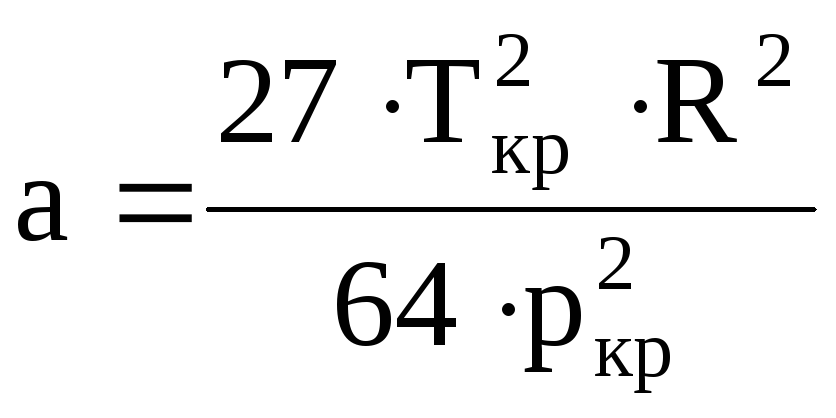 ;
;![]() (19)
(19)
![]()
Ван-дер-Ваальс нашел, что поправка bна собственный объём молекул, имеющих
шарообразную форму, равна учетверённому
объёму молекул.
Уравнение (17) приближенное. Коэффициенты
аиbв действительности
являются сложными функциями объёма,
температуры, формы молекул газа.
Критическая температура чистого вещества
– это максимальная температура, при
которой жидкая и паровая фазы могут
сосуществовать в равновесии, или та
температура, при которой средняя
молекулярная кинетическая энергия
становится равной потенциальной энергии
притяжения молекул. При более высокой
температуре существование жидкой фазы
невозможно.
Давление
паров вещества при критической температуре
называется критическим давлением, а
объём вещества, отнесенный к одному
молю или другой единице массы вещества,
называется критическим удельным объёмом.
Критической принято называть такую
температуру, выше которой газ под
действием давления любого значения не
может быть обращен в жидкость.
На рис. 1. приведена зависимость давления
(упругости насыщенных паров) чистых
веществ от температуры. Эта зависимость
более точно описывает изменение свойств
реальных газов при давлениях до 10 МПа
и температурах от 283 до 293 К, но она не
может численно описывать изменение,
свойств многокомпонентных смесей
месторождений природных газов.
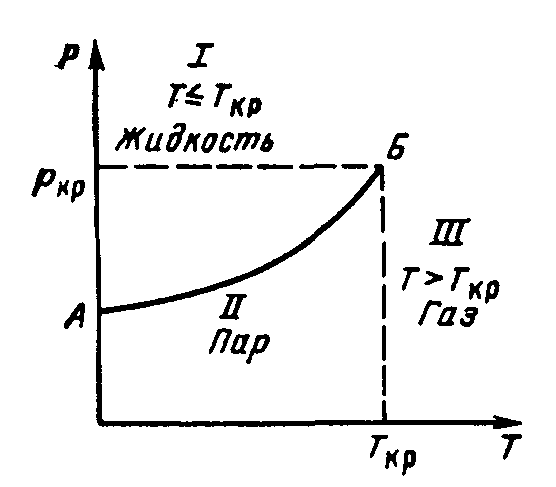
Рисунок
1. Зависимость давления (упругости
насыщенных паров) чистых веществ от
температуры
Давление, необходимое для сжижения газа
при критической температуре, называется
критическим. Кроме критического давления
и критической температуры вводится
понятие критического объёма, равного
объёму одного моля газа при критических
давлении и температуре. Для природных
газов, представляющих собой смесь
отдельных компонентов, значения Ркр
и Ткр определяются
как среднекритические (псевдокритические).
Средние критические давление и температуру
смеси можно определить по формулам:
![]() (20)
(20)
![]()
где х1, х2…хn– объёмные доли компонентов, входящих
в состав газа;
![]() –критические давления компонентов;
–критические давления компонентов;
![]() – критические температуры компонентов.
– критические температуры компонентов.
Следует отметить, что коэффициент
сверхсжимаемости природной углеводородной
смеси Zсмможно определить по
графической зависимости представленной
на рисунке 1.2.
Если известна относительная плотность
газа
![]()
![]() ,
,
то средние критические давление и
температуру природного газа можно
определить по графикам.![]() При содержании в природном газеN2,
При содержании в природном газеN2,
СО2илиH2Sв значенияРкр иТкрвводятся соответствующие поправки.
Когда содержаниеN2,CO2или Н2Sпревышает 15% об., вместо графиков для
определенияРкриТкрследует пользоваться формулой (1.20).
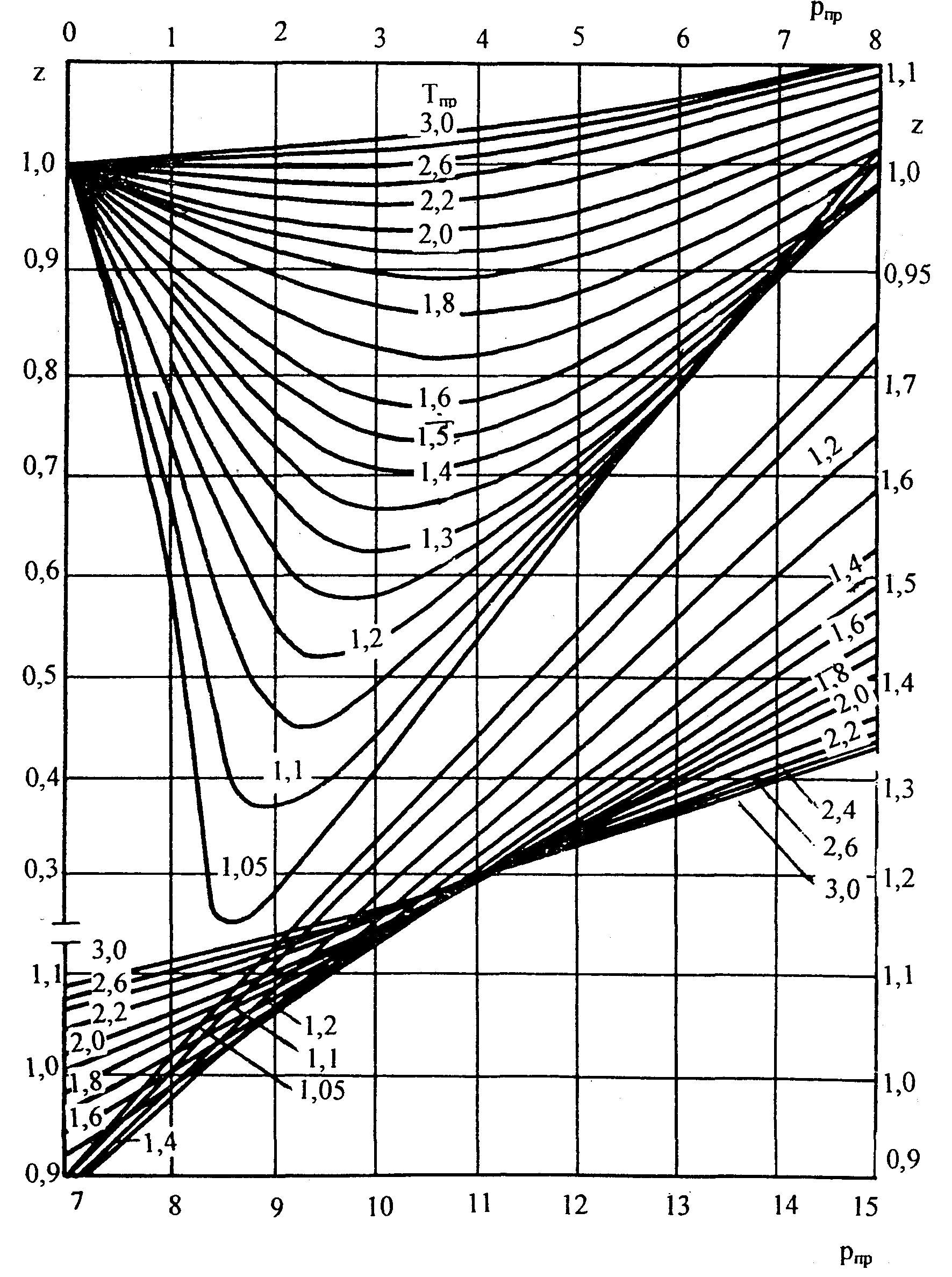
Рис. 1.2. Значение коэффициента
сверхсжимаемости z
по данным Стэндинга и Катца
Для приближенных расчётов при изменении
![]()
![]() ,
,
от 0,5 до 0,9 значенияРкриТкрможно определить
по формулам:
![]() ,
,
МПа (21)
![]() ,
,
К
Часто в расчётах, например, при определении
вязкости и коэффициента сверхсжимаемости
газа, пользуются так называемыми
приведенными давлениями и температурами.
Приведенными параметрами индивидуальных
компонентов называют безразмерные
величины, показывающие, во сколько раз
действительные параметры состояния
газа (давление, абсолютная температура,
объём, плотность, коэффициент отклонения)
больше или меньше критических:
Приведенным давлением Рпрназывается отношение давления газаРк его критическому давлениюРкр
![]() (22)
(22)
Приведенной температурой газа Тпрназывается отношение абсолютной
температуры газаТк его критическому
значению:
![]() ,
,
(23)
Дальнейший прогресс науки и техники
потребовал разработки более точного
уравнения состояния природных газов,
способного правильно описывать изменение
их свойств при давлениях до 100 МПа и
температурах до 573 К в процессах добычи
газа и при давлениях до 20 МПа и низких
температурах до 223 – 93 К (от минус 50 до
минус180°С) в процессах переработки
природных газов.
В решении этой проблемы выявились два
направления:
1) введение поправочного коэффициента
zв уравнение состояния
идеального газа (1.17), учитывающего
отклонение реального газа от идеального,
т. е.pV==zRT
2) дополнение уравнения состояния
идеального газа большим числом констант.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Введение
Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].
Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.
Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.
К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.
В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.
Математическая модель определения плотности газа
Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:
1. Уравнение Менделеева-Клапейрона:
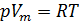 (1),
(1),
где:
 — давление газа;
— давление газа;
 — молярный объём;
— молярный объём;
R — универсальная газовая постоянная,
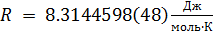 ;
;
T — абсолютная температура, T=273.16 К.
2. Два измеряемых параметра:
p – давление газа, Па
t – температура газа, °С.
Известно, что молярный объём  зависит от объёма газа V и количества молей газа
зависит от объёма газа V и количества молей газа 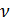 в этом объёме:
в этом объёме:
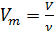 (2)
(2)
Также известно, что
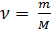 (3),
(3),
где: m – масса газа, M – молярная масса газа.
Учитывая (2) и (3) перепишем (1) в виде:
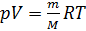 (4).
(4).
Как известно, плотность вещества
 равна:
равна:
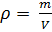 (5).
(5).
Из (4) и (5) выведем уравнение для плотности газа
 :
:
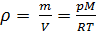 (6)
(6)
и введём обозначение параметра
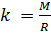 , который зависит от молярной массы газовой смеси:
, который зависит от молярной массы газовой смеси:
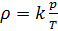 (7).
(7).
Если состав газовой смеси не меняется, то параметр k является константой.
Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.
Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.
Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:
- 23 % по весу из молекул кислорода

- 76 % по весу из молекул азота
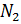
- 1 % по весу из атомов аргона
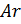
Молярные массы этих веществ воздуха будут соответственно равны:
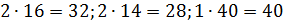 , г/моль.
, г/моль.
Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:
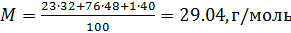
Теперь, зная значение константы
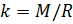 , мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений
, мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений
 и t:
и t:
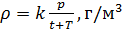
Приведение плотности газа к нормальным, стандартным условиям
Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].
Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.
Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.
Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.
Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура 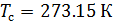 и абсолютное давление
и абсолютное давление 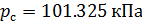 :
:
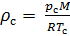 (9).
(9).
Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для 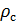 :
:
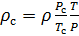 (10).
(10).
Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура 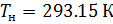 и абсолютное давление
и абсолютное давление
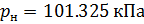 :
:
 (11).
(11).
В уравнениях (10) и (11) используем значения параметров воздуха  , T и P из уравнения (8), полученные в рабочих условиях.
, T и P из уравнения (8), полученные в рабочих условиях.
Реализация измерительного канала давления и температуры
Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.
Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).
Для этого, на аппаратном уровне, нам понадобятся компоненты:
- Arduino (Uno, …) – используем как программатор;
- микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
- кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
- тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
- BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
- преобразователь интерфейсов TTL/USB;
- расходные материалы – провода, припой, монтажная плата, и др.
Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.
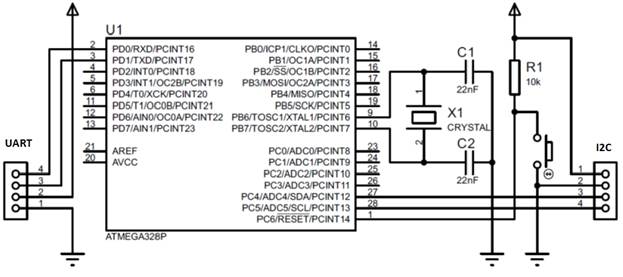
Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры
Теперь рассмотрим этапы осуществления нашей задачи.
1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.
2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.
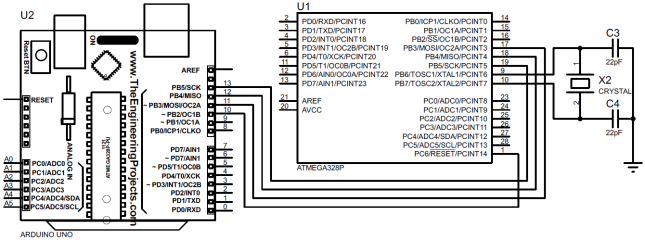
Рис. 2 – Схема подключения микроконтроллера к программатору
3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.

Рис. 3 Система измерения давления и температуры
Листинг 1 – Программа опроса измерительного преобразователя давления и температуры
#include <SFE_BMP180.h>
SFE_BMP180 pressure;
double T,P;
void setup()
{
Serial.begin(9600);
pressure.begin();
}
void loop()
{
P = getPressure();
Serial.println(P+0.5, 2);
Serial.println(T+0.54, 2);
delay(1000);
}
double getPressure(){
char status;
status = pressure.startTemperature();
if (status != 0){
delay(status); // ожидание замера температуры
status = pressure.getTemperature(T);
if (status != 0){
status = pressure.startPressure(3);
if (status != 0){
delay(status); // ожидание замера давления
status = pressure.getPressure(P,T);
if (status != 0){
return(P);
}
}
}
}
}
Программа Python для фильтрации по каналам температуры и давления, и получение результатов
Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.
Листинг 2 – Определение плотности газа по результатам измерения давления и температуры
import numpy as np
import matplotlib.pyplot as plt
import serial
from drawnow import drawnow
import datetime, time
from pykalman import KalmanFilter
#вводим матрицу перехода и матрицу наблюдений
transition_matrix = [[1, 1, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 0, 0, 1]]
observation_matrix = [[1, 0, 0, 0],
[0, 0, 1, 0]]
#вводим и инициируем матрицу измерений
initial_state_mean = [101000,
0,
28,
0]
#параметры уравнения состояния идеального газа:
#универсальная газовая постоянная R, [Дж/(моль*К)]
R = 8.314459848
#молярная масса воздуха M, [г/моль]
M = 29.04
#коэффициент k = M/R, [г/(Дж*К)]
k = M / R
#абсолютная температура, [K]
K = 273.16
#стандартное (нормальное) давление, [Па]
Pn = 101325
#определяем количество измерений
# общее количество измерений
str_m = input("введите количество измерений: ")
m = eval(str_m)
# количество элементов выборки
mw = 16
#настроить параметры последовательного порта
ser = serial.Serial()
ser.baudrate = 9600
port_num = input("введите номер последовательного порта: ")
ser.port = 'COM' + port_num
ser
#открыть последовательный порт
try:
ser.open()
ser.is_open
print("соединились с: " + ser.portstr)
except serial.SerialException:
print("нет соединения с портом: " + ser.portstr)
raise SystemExit(1)
#определяем списки
l1 = [] # для значений 1-го параметра
l2 = [] # для значений 2-го параметра
t1 = [] # для моментов времени
lw1 = [] # для значений выборки 1-го параметра
lw2 = [] # для значений выборки 2-го параметра
n = [] # для значений моментов времени
nw = [] # для значений выборки моментов времени
l1K = [] # для фильтрованных значений 1-го параметра
l2K = [] # для фильтрованных значений 2-го параметра
ro = [] # для плотности газовой среды
#подготовить файлы на диске для записи
filename = 'count.txt'
in_file = open(filename,"r")
count = in_file.read()
count_v = eval(count) + 1
in_file.close()
in_file = open(filename,"w")
count = str(count_v)
in_file.write(count)
in_file.close()
filename = count + '_' + filename
out_file = open(filename,"w")
#вывод информации для оператора на консоль
print("nпараметры:n")
print("n - момент времени, с;")
print("P - давление, Па;")
print("Pf - отфильтрованное значение P, Па;")
print("T - температура, град. С;")
print("Tf - отфильтрованное значение T, град. С;")
print("ro - плотность воздуха, г/м^3;")
print("nизмеряемые значения величин параметровn")
print('{0}{1}{2}{3}{4}{5}n'.format('n'.rjust(3),'P'.rjust(10),'Pf'.rjust(10),
'T'.rjust(10),'Tf'.rjust(10),'ro'.rjust(10)))
#считываение данных из последовательного порта
#накопление списков
#формирование текущей выборки
i = 0
while i < m:
n.append(i)
nw.append(n[i])
if i >= mw:
nw.pop(0)
ser.flushInput() #flush input buffer, discarding all its contents
line1 = ser.readline().decode('utf-8')[:-1]
line2 = ser.readline().decode('utf-8')[:-1]
t1.append(time.time())
if line1:
l = eval(line1)
#l = np.random.normal(l,100.0)
l1.append(l)
lw1.append(l1[i])
if i >= mw:
lw1.pop(0)
if line2:
l = eval(line2)
#l = np.random.normal(l,1.5)
l2.append(l)
lw2.append(l2[i])
if i >= mw:
lw2.pop(0)
#-------------------------
initial_state_mean = [l1[i],0,l2[i],0]
kf1 = KalmanFilter(transition_matrices = transition_matrix,
observation_matrices = observation_matrix,
initial_state_mean = initial_state_mean)
if i == 0:
measurements = np.array( [ [l1[i], l2[i]],
[initial_state_mean[0], initial_state_mean[2]] ] )
measurements = np.array( [ [l1[i], l2[i]],
[l1[i-1], l2[i-1]] ] )
kf1 = kf1.em(measurements, n_iter=2)
(smoothed_state_means, smoothed_state_covariances) = kf1.smooth(measurements)
l1K.append(smoothed_state_means[0, 0])
l2K.append(smoothed_state_means[0, 2])
#плотность воздуха в рабочих условиях
#ro.append( k * l1K[i]/( l2K[i] + K) )
#плотность воздуха, приведенная к стандартным условиям
ro.append( (k * l1K[i]/( l2K[i] + K)) * (Pn*(l2K[i]+K)/K/l1K[i]) )
#плотность воздуха, приведенная к нормальным условиям
#ro.append( (k * l1K[i]/( l2K[i] + K)) * (Pn*(l2K[i]+K)/(K+20)/l1K[i]) )
print('{0:3d} {1:10.3f} {2:10.3f} {3:10.3f} {4:10.3f} {5:10.3f}'.
format(n[i],l1[i],l1K[i],l2[i],l2K[i],ro[i]))
i += 1
ser.close()
time_tm = t1[m - 1] - t1[0]
print("nпродолжительность времени измерений: {0:.3f}, c".format(time_tm))
Ts = time_tm / (m - 1)
print("nпериод опроса датчика: {0:.6f}, c".format(Ts))
#запись таблицы в файл
print("nтаблица находится в файле {}n".format(filename))
for i in np.arange(0,len(n),1):
out_file.write('{0:3d} {1:10.3f} {2:10.3f} {3:10.3f} {4:10.3f} {5:10.3f}n'.
format(n[i],l1[i],l1K[i],l2[i],l2K[i],ro[i]))
#закрыть файл с таблицей
out_file.close()
now = datetime.datetime.now() #получаем дату и время
#выводим графики
plt.figure('давление')
plt.plot( n, l1, "b-", n, l1K, "r-")
plt.ylabel(r'$давление, Па$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
plt.figure('температура')
plt.plot( n, l2, "b-", n, l2K, "r-")
plt.ylabel(r'$температура, degree С$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
plt.figure('плотность воздуха')
plt.plot( n, ro, "r-")
plt.ylabel(r'$плотность воздуха, г/м^3$')
plt.xlabel(r'$номер измерения$' +
'; (период опроса датчика: {:.6f}, c)'.format(Ts))
plt.title("BMP180n(" +
now.strftime("%d-%m-%Y %H:%M") + ")")
plt.grid(True)
plt.show()
Результаты расчёта представлены листингом и рис. 4, 5, 6.
Интерфейс пользователя и таблица результатов расчёта
введите количество измерений: 33
введите номер последовательного порта: 6
соединились с: COM6
параметры:
n - момент времени, с;
P - давление, Па;
Pf - отфильтрованное значение P, Па;
T - температура, град. С;
Tf - отфильтрованное значение T, град. С;
ro - плотность воздуха, г/м^3;
измеряемые значения величин параметров
n P Pf T Tf ro
0 101141.000 101141.000 28.120 28.120 1295.574
1 101140.000 101140.099 28.190 28.183 1295.574
2 101140.000 101140.000 28.130 28.136 1295.574
3 101141.000 101140.901 28.100 28.103 1295.574
4 101140.000 101140.099 28.100 28.100 1295.574
5 101141.000 101140.901 28.110 28.109 1295.574
6 101141.000 101141.000 28.100 28.101 1295.574
7 101139.000 101139.217 28.100 28.100 1295.574
8 101138.000 101138.099 28.090 28.091 1295.574
9 101137.000 101137.099 28.100 28.099 1295.574
10 101151.000 101149.028 28.100 28.100 1295.574
11 101136.000 101138.117 28.110 28.109 1295.574
12 101143.000 101142.052 28.110 28.110 1295.574
13 101139.000 101139.500 28.100 28.101 1295.574
14 101150.000 101148.463 28.110 28.109 1295.574
15 101154.000 101153.500 28.120 28.119 1295.574
16 101151.000 101151.354 28.110 28.111 1295.574
17 101141.000 101142.391 28.130 28.127 1295.574
18 101141.000 101141.000 28.120 28.121 1295.574
19 101142.000 101141.901 28.110 28.111 1295.574
20 101141.000 101141.099 28.120 28.119 1295.574
21 101142.000 101141.901 28.110 28.111 1295.574
22 101146.000 101145.500 28.120 28.119 1295.574
23 101144.000 101144.217 28.130 28.129 1295.574
24 101142.000 101142.217 28.130 28.130 1295.574
25 101142.000 101142.000 28.140 28.139 1295.574
26 101142.000 101142.000 28.130 28.131 1295.574
27 101146.000 101145.500 28.150 28.147 1295.574
28 101142.000 101142.500 28.190 28.185 1295.574
29 101146.000 101145.500 28.230 28.225 1295.574
30 101146.000 101146.000 28.230 28.230 1295.574
31 101146.000 101146.000 28.220 28.221 1295.574
32 101150.000 101149.500 28.210 28.211 1295.574
продолжительность времени измерений: 6.464, c
период опроса датчика: 0.201998, c
таблица находится в файле 68_count.txt
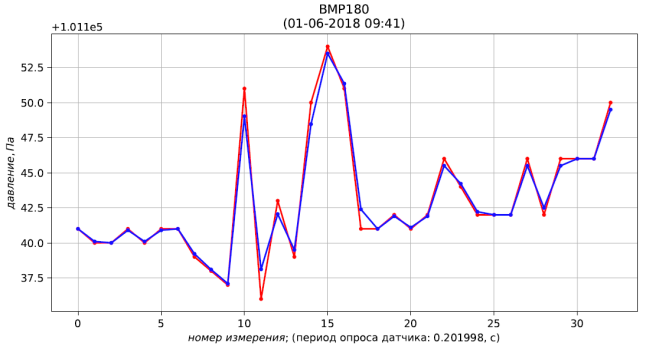
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления
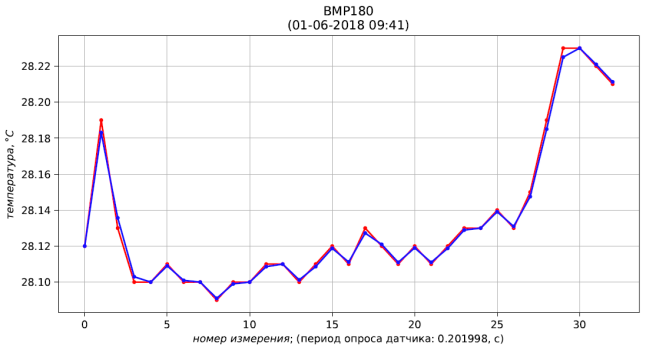
Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры
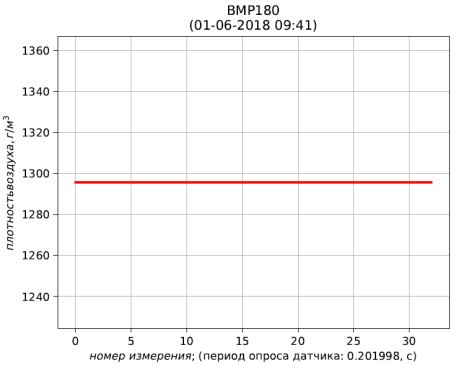
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)
Выводы
Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.
Ссылки на источники информации
- ГОСТ 8.586.5-2005. URL
- ГОСТ Р 8.740 – 2011. URL
- Ideal gas law. URL
- Standard conditions for temperature and pressure. URL
Задания Д6 B9 № 5959 

Газ нагревают изобарически. Зависимость плотности этого газа от температуры правильно изображена на рисунке
1) 1
2) 2
3) 3
4) 4
Спрятать решение
Решение.
Напишем уравнение состояния идеального газа и из него найдём плотность газа:
При изобарическом процессе давление постоянно, следовательно, плотность зависит только от температуры и обратно пропорциональна ей. Зависимость плотности этого газа от температуры правильно изображена на рисунке 2.
Правильный ответ указан под номером 2.
Примечание. Нужно обратить внимание на то, что в ответах даны зависимости плотности газа от температуры, а не давления от температуры. Греческая буква ро и латинская p похожи, но их следует различать.
Подборка по базе: Задачи на определение прибыли и рентабельности.docx, Задача № 1 Определение диаметра штуцера фонтанной арматуры.pdf, Ур.12.Виды компьютерной памяти и их сравнение. Свойства оператив, 07.05Игра, как средство развития физических качеств старших школ, Анализ конкурентов на рынке и определение собственной конкуренто, 5.05.23 Определение качества антифриза.docx, Самостоятельная работа по теме « Свойства Квадратный корень» (1), Гетеропереходы и их физические свойства.docx, ЛБ-2 Определение длительности производственного цикла.pdf, уникальные свойства НМ.docx
Определение физических свойств природного газа
Исходные данные:
| СН4 | С2Н6 | С3Н8 | С4Н10 | С5Н+12 | СО2 | Н2S | N2 | |
| gi | 0,312 | 0,165 | 0,191 | 0,084 | 0,022 | 0,014 | 0,014 | 0,198 |
| ρi | 0,6679 | 1,263 | 1,873 | 2,5185 | 3,22 | 1,848 | 1,848 | 1,205 |
| Mi | 16,042 | 30,07 | 44,09 | 58,12 | 72,15 | 44,01 | 44,01 | 28,016 |
| Pкр | 46,95 | 49,76 | 43,33 | 38,7 | 34,35 | 75,27 | 75,27 | 34,65 |
| Ткр | 190,55 | 305,43 | 369,82 | 425,16 | 469,65 | 304,2 | 304,2 | 126,26 |
Порядок вычислений:
1. Вычислим плотность газа:
Плотность – это масса газа в единице объема газа. Размерность плотности в системе СИ – кг/м3. Плотность газа определенного состава определяется как сумма произведений плотности отдельных компонентов на их объемное содержание:

2. Вычислим среднюю молекулярную массу:
Молекулярная масса определяется как сумма произведений молекулярной массы отдельных компонентов на их объемное содержание. Размерность молекулярной массы в системе СИ – кг/моль:

3. Вычислим критическое давление:
Критическое давление (Ркр) – давление, соответствующее критической точке, выше которой в однокомпонентной системе жидкая и газовая фаза вещества не могут равновесно существовать. Размерность критического давления в системе СИ – кг/см2. Критическое давление газа определяется как сумма произведений критических давлений отдельных компонентов на их объемное содержание:

4. Вычислим критическую температуру:
Критическая температура (Ткр) – температура, выше которой газ не может быть превращен в жидкость, ни при каком давлении. Размерность критической температуры в системе СИ – К. Критическая температура газа определяется как сумма произведений критических температур отдельных компонентов на их объемное содержание:

5. Вычислим относительную плотность газа по воздуху:
Относительная плотность газа – отношение масс равных объемов сухого газа и сухого воздуха при одинаковых условиях по температуре и давлению.

где: ρв = 1,205 кг/м3 при t = 20 ᵒС, Р = 760 мм.рт.ст.
6. Определим псевдокритическое давление и температуру Псевдокритическое давление и температура – это расчетные Ркр и Ткр для смеси газов. Для определения псевдокритического давления и температуры воспользуемся графиком (рис.1.1)

Рис. 1.1 Зависимость псевдокритического давления Рпр.кр. и псевдокритической температуры Тпр.кр. от относительной плотности газа по воздуху ρ
Рп.кр. = 45,7 кг/см2 Тп.кр. = 285 К
7. Вычислим приведенные параметры:
Приведенными параметрами называются отношения соответствующих параметров к их критическим значениям:


Критические и приведенные параметры позволяют использовать принцип соответственных состояний для определения коэффициента сверхсжимаемости z, вязкости некоторых других характеристик газа.
8. Определим коэффициент сверхсжимаемости:
Коэффициент сверхсжимаемости (Z) – отношение объемов равного числа молей реального и идеального газов при одних и тех же термобарических условиях. Основной диапазон изменения Z: 0,8-1,2. Z – мера отклонения реального газа от идеального. Для определения коэффициента сверхсжимаемости можно воспользоваться графиком (рис.1.2).

Рис. 1.2 Зависимость коэффициента сверхсжимаемости природного газа Z от приведенных абсолютных давлений Рпр и температуры Тпр
Z=0,45
9. Вычислим плотность газа в зависимости от давления, температуры и коэффициента сверхсжимаемости:

10. Определим вязкость газа:
Вязкостью газа (μг) – свойство газа оказывать сопротивление при перемещении одних частиц относительно других. Размерность вязкости газа в системе СИ – мПа·с. Для определения вязкости газа воспользуемся графиками (рис.1.3, 1.4).


Рис. 1.3 Зависимость вязкости углеводородных газов от относительной плотности газа по воздуху
μа =0,0076 мПа·с

Рис. 1.4 Зависимость отношения вязкостей от приведенного давления Рпр при различных приведенных температурах Тпр
μ* =7
Расчет физических свойств пластовой нефти
Исходные данные:
Рпл = 180 атм;
Р11 = 100;
tпл = 67 ᵒС;
ρнст = 825 кг/м3;
Rг = 41 м3/м3;
ρгст = 1,201 кг/м3;
Мн = 140 кг/моль;
RB = 17 м3/м3;
βB = 4,5·10-4 1/Мпа;
Концентрация солей С = 6%.
Порядок вычислений:
1. Вычислим плотность пластовой нефти:
Плотность пластовой нефти (ρпл) равна массе нефти, содержащейся в единице объема при пластовых условиях, определяется по глубинным пробам нефти в лабораторных условиях. Пластовая нефть кроме жидкой фазы содержит в себе и газовую фазу. В этом смысле пластовая нефть есть газонасыщенная пластовая жидкость. Зная состав пластовой нефти и газонасыщенность, плотность пластовой нефти ρпл можно определить с помощью аналитической формулы:

где:
ρнст – плотность разгазированной нефти в стандартных условиях, кг/м3;
ρгст – плотность газа стандартного разгазирования газонасыщенной нефти, кг/м3;
Rг – газонасыщенность м3/м3.
2. Вычислим коэффициент сжимаемости нефти
Объемный коэффициент пластовой нефти характеризует изменение объема жидкой фазы при изменении термодинамических условий. Величина объемного коэффициента bн показывает кратность уменьшения объема, занимаемого нефтью в пласте Vпл , по сравнению с объемом жидкой фазы Vж нефтегазовой системы при заданных давлении и температуре V(T,P):

где:
ρгст – плотность выделившегося газа в стандартных условиях, кг/м3;
ρнпл – плотность газонасыщенной нефти в пластовых условиях, кг/м3;
ρн – плотность нефти при заданных давлении и температуре, кг/м3;
Rг – газонасыщенность м3/м3.
Расчет физических свойств пластовой воды
1. Вычислим коэффициент сжимаемости пластовой воды:
Сжимаемость воды (βВ) – это обратимое изменение объема воды в пластовых условиях под действием давления. Коэффициент сжимаемости воды изменяется в пластовых условиях в пределах 3,7·10-10 – 5,0·10-10 Па-1

где:
βГ.В – коэффициента сжимаемости чистой негазированной воды, 1/МПа·10-4;
К – коэффициента Сеченова;
Gг – коэффициент растворимости естественного газа в чистой воде, м3/м3;
C – массовая концентрация солей, %.
Определяем коэффициент сжимаемости βГ.В чистой негазированной воды по графику (рис. 1.5) в зависимости от давления и температуры;

Рис. 1.5 Кривые изменения коэффициента сжимаемости βГ.В
чистой негазированной воды в зависимости от давления и температуры
Определяем коэффициент растворимости естественного газа Gг в чистой воде по графику (рис. 1.6) в зависимости от давления и температуры;

Рис. 1.6 Кривые изменения коэффициента Gг растворимости естественного газа в чистой воде в зависимости от давления и температуры
Определяем коэффициент Сеченова – К по графику (рис. 1.7) в зависимости от температуры.

Рис. 1.7 График зависимости коэффициента Сеченова К от температуры Т
2. Вычислим плотность пластовой воды по формуле:
Плотность пластовой воды ρв (Р,Т,С) есть функция давления P, температуры T, концентрации растворенных солей C, и газонасыщенности. При известном коэффициенте сжимаемости газонасыщенной воды плотность пластовой воды рассчитывается по формуле:

где:
ρВСТ – плотность воды в стандартных условиях, кг/м3;
a – термический коэффициент объемного расширения воды, равный а=5·10-4, 1/K;
βВ– коэффициент сжимаемости газонасыщенной пластовой воды, 1/МПа;
RВ – газосодержание воды, м3/м3;
Плотность пластовой воды в стандартных условиях вычисляется по формуле:

где: С – массовая концентрация солей, %.
3. Вычислим объемный коэффициент пластовой воды:
Вязкость пластовой воды μВ есть функция температуры и концентрации солей. Влияние давления незначительно. Вязкость пластовой воды в диапазоне температур от 20 до 100 ᵒС при концентрации солей не выше 6% рассчитывается по формуле:

Определение коэффициента упругоемкости пласта
1. Вычислим сжимаемость скелета пласта:

где: m – пористость пласта.
2. Вычислим коэффициент упругоемкости пласта:
Коэффициент упругоемкости пласта β* характеризует упругие свойства скелета и насыщающей его пластовой жидкости.

где:
βB– сжимаемость воды, Па-1;
βC – сжимаемость скелета пласта, 1/МПа.
 0,88
0,88
где:
SB – насыщенность пор связанной водой, в долях от объема пор;
nB – водонасыщенность пласта, в долях.
Ответы на контрольные вопросы
1. Дать определение природному газу и нефти.
Природный газ – полезное ископаемое, представляющее собой смесь газообразных углеводородов природного происхождения, состоящую главным образом из метана и примесей других алканов. Иногда в составе также присутствует некоторое количество углекислого газа, азота, сероводорода и гелия.
Природная нефть – легко воспламеняющаяся жидкость, которая находится в глубоких осадочных отложениях и хорошо известна благодаря ее использованию в качестве топлива и сырья для химического производства.
2. Расскажите как определяется плотность пластовой нефти и воды.
Пластовая нефть кроме жидкой фазы содержит в себе и газовую фазу. В этом смысле пластовая нефть есть газонасыщенная пластовая жидкость. Зная состав пластовой нефти и газонасыщенность, плотность пластовой нефти ρпл можно определить с помощью аналитической формулы:

При известном коэффициенте сжимаемости газонасыщенной воды плотность пластовой воды рассчитывается по формуле:

3. Что характеризует объемный коэффициент пластовой нефти bн и пластовой воды bв?
Объемный коэффициент пластовой нефти показывает изменение объема нефти в пластовых условиях в результате изменения условий давления и температуры, но главным образом в результате выделения из нефти растворенного газа.
Объёмный коэффициент пластовой воды характеризует отношение удельного объёма воды в пластовых условиях к удельному объёму воды в стандартных условиях.
4. Расскажите от чего зависит вязкость пластовой нефти μн.
Вязкость пластовой нефти всегда значительно отличается от вязкости сепарированной вследствие большого количества растворенного газа, повышенной пластовой температуры и давления. При этом все нефти подчиняются следующим общим закономерностям: вязкость их уменьшается с повышением количества газа в растворе, с увеличением температуры; повышение давления вызывает некоторое увеличение вязкости.
5. Напишите формулу расчета вязкости пластовой воды μв.

6. Что называется относительной плотностью газа ρ.
Относительная плотность газов — безразмерная величина, она показывает, какой из газов тяжелее (имеет большую плотность) и во сколько раз. Она равна отношению молярных масс газов, поэтому позволяет определить молярную массу неизвестного газа.
7. Дайте определение критического давления и температуры Ркр, Ткр.
Критическое давление – это давление, при котором газ еще не переходит в жидкое состояние, какова бы ни была температура.
Критическая температура – это наибольшая температура, при которой газ еще не переходит в жидкое состояние, как бы велико ни было давление.
8. Что такое коэффициент сжимаемости газа z и как его определить графическим и аналитическим методами?
Коэффициент сверхсжимаемости газов – отношение объёма газа при заданных термобарических условиях к объёму этого газа, определённому при идентичных термобарических условиях по законам идеального газа. Другими словами, коэффициент сверхсжимаемости характеризует отклонение объёма реального газа от объёма идеального газа.
Из определения коэффициента сверхсжимаемости следует, что:

Для определения коэффициента сверхсжимаемости можно воспользоваться графиком (рис.1.2).
9. Что характеризует коэффициент сжимаемости нефти?
Коэффициент сжимаемости характеризует относительное приращение объема нефти при изменении давления на единицу.
10. Дать определение упругоемкости пласта.
Упругоемкость пласта характеризует упругие свойства скелета и насыщающей его пластовой жидкости.
11. От каких параметров пласта и жидкости зависит коэффициент упругоемкости пластовой системы?
Коэффициент упругоемкости пластовой системы зависит от следующих параметров: пористость пласта, сжимаемость воды, сжимаемость скелета пласта, насыщенность пор связанной водой, в долях от объема пор, водонасыщенность пласта, в долях.
