Density is mass per unit volume. Finding the density of a gas is the same as finding the density of a solid or liquid. You have to know the mass and the volume of the gas. The tricky part with gases is that you are often given pressures and temperatures with no mention of volume. You have to figure it out from the other information.
How to Find Density of a Gas
- Calculating the density of a gas usually involves combining the formula for density (mass divided by volume) and the ideal gas law (PV = nRT).
- ρ = PM/RT, where M is molar mass.
- The ideal gas law is a good approximation of the behavior of real gases.
- Usually, with this type of problem, you are given the type of gas and enough other variables to solve the ideal gas law problem.
- Remember to convert temperature to absolute temperature and watch your other units.
Density of a Gas Example Calculation
This example problem will show how to calculate density of a gas when given the type of gas, the pressure, and the temperature.
Question: What is the density of oxygen gas at 5 atm and 27 °C?
First, let’s write down what we know:
Gas is oxygen gas or O2.
Pressure is 5 atm
Temperature is 27 °C
Let’s start with the Ideal Gas Law formula.
PV = nRT
where
P = pressure
V = volume
n = number of moles of gas
R = gas constant (0.0821 L·atm/mol·K)
T = absolute temperature
If we solve the equation for volume, we get:
V = (nRT)/P
We know everything we need to find the volume now except the number of moles of gas. To find this, remember the relationship between number of moles and mass.
n = m/MM
where
n = number of moles of gas
m = mass of gas
MM = molecular mass of the gas
This is helpful since we needed to find the mass and we know the molecular mass of oxygen gas. If we substitute for n in the first equation, we get:
V = (mRT)/(MMP)
Divide both sides by m:
V/m = (RT)/(MMP)
But density is m/V, so flip the equation over to get:
m/V = (MMP)/(RT) = density of the gas.
Now we need to insert the values we know.
MM of oxygen gas or O2 is 16+16 = 32 grams/mole
P = 5 atm
T = 27 °C, but we need absolute temperature.
TK = TC + 273
T = 27 + 273 = 300 K
m/V = (32 g/mol · 5 atm)/(0.0821 L·atm/mol·K · 300 K)
m/V = 160/24.63 g/L
m/V = 6.5 g/L
Answer: The density of the oxygen gas is 6.5 g/L.
Another Example
Calculate the density of carbon dioxide gas in the troposphere, knowing the temperature is -60.0 °C and the pressure is 100.0 millibar.
First, list what you know:
- P = 100 mbar
- T = -60.0 °C
- R = 0.0821 L·atm/mol·K
- carbon dioxide is CO2
Right off the bat, you can see some units don’t match up and that you need to use the periodic table to find the molar mass of carbon dioxide. Let’s start with that.
- carbon mass = 12.0 g/mol
- oxygen mass = 16.0 g/mol
There is one carbon atom and two oxygen atoms, so the molar mass (M) of CO2 is 12.0 + (2 x 16.0) = 44.0 g/mol
Converting mbar to atm, you get 100 mbar = 0.098 atm. Converting °C to K, you get -60.0 °C = 213.15 K.
Finally, all of the units agree with those found in the ideal gas constant:
- P = 0.98 atm
- T = 213.15 K
- R = 0.0821 L·atm/mol·K
- M = 44.0 g/mol
Now, plug the values into the equation for the density of a gas:
ρ = PM/RT = (0.098 atm)(44.0 g/mol) / (0.0821 L·atm/mol·K)(213.15 K) = 0.27 g/L
Sources
- Anderson, John D. (1984). Fundamentals of Aerodynamics. McGraw-Hill Higher Education. ISBN 978-0-07-001656-9.
- John, James (1984). Gas Dynamics. Allyn and Bacon. ISBN 978-0-205-08014-4.
- Khotimah, Siti Nurul; Viridi, Sparisoma (2011). “Partition function of 1-, 2-, and 3-D monatomic ideal gas: A simple and comprehensive review”. Jurnal Pengajaran Fisika Sekolah Menengah. 2 (2): 15–18.
- Sharma, P. V. (1997). Environmental and Engineering Geophysics. Cambridge University Press. ISBN 9781139171168. doi:10.1017/CBO9781139171168
- Young, Hugh D.; Freedman, Roger A. (2012). University Physics with Modern Physics. Addison-Wesley. ISBN 978-0-321-69686-1.
Комбинированный газовый закон — это формула, которая связывает основные параметры идеального газа и позволяет вычислять неизвестные в случаях, если заданы пять остальных величин.
Идеальный газ
Идеальный газ — это математическая модель с определенными допущениями, которая позволяет исследовать свойства газообразных веществ с достаточной точностью. К допущениям, которые используются в модели идеального газа, относятся:
- пренебрежение размерами молекул;
- силы молекулярного взаимодействия не учитываются;
- соударение атомов и молекул абсолютно упруго;
- газ находится в термодинамическом равновесии.
Благодаря этим допущениям ученые изучили основные свойства газообразных веществ и вывели основные законы, которым подчиняются любые газы. Комбинированный закон объединяет все перечисленные ниже зависимости.
Газовые законы
Любое газообразное вещество характеризуется тремя простыми параметрами: объемом, давлением и температурой. Газ тем и хорош, что он заполняет весь предоставленный объем или может сжиматься до минимальных объемов, иногда переходя в состояние жидкости. Сжимать газ можно двумя способами:
- при постоянном давлении уменьшить температуру;
- при постоянной температуре увеличить давление.
Эти две простые формулировки отражают в себе два известных газовых закона: изобару и изотерму. В изобарном процессе изменение температуры приводит к прямо пропорциональному изменению объема. Вспомните жидкий азот: он занимает минимум места, при этом его температура составляет 63,29 К, что соответствует –209 градусам Цельсия. Если температуру азота поднять до 20 градусов Цельсия, то 1 литр жидкого азота превратится в 700 литров газа. Увеличивается температура, увеличивается объем и наоборот. Эти изменения обусловлены тем, что соотношение объема к температуре газа остается статичным.
В изотермическом процессе температура не изменяется и для сжатия газа придется увеличить давление. Это процесс проще для понимания, так как сдавливая газ мы уменьшаем его объем подобно тому, как утрамбовывание грунта или снега позволяет уложить их более плотно и с меньшим объемом. В этом изотермическом процессе изменение давления приводит к обратно пропорциональному изменению объема. Больше давление, меньше объем и наоборот. Такая динамика обусловлена тем, что произведение давления на объем — это всегда постоянная величина.
Если же объем газа не изменяется, то процесс называется изохорным и в этом процессе отображается взаимосвязь давления и температуры. Согласно закону, изменение одного параметра вызывает прямо пропорциональное изменение другого. Это означает, что увеличение давления в сосуде вызывает рост температуры находящегося там газа. Верно и обратное утверждение.
Комбинированный закон
Все перечисленные законы подчиняются общей формулировке: при постоянстве одного параметра, отношение двух других также постоянно. Обобщая эти законы в динамике получаем комбинированный газовый закон, который описывается формулой:
где P1, V1 и T1 — соответственно начальные давление, объем и температура, а P2, V2 и T2 — конечные.
Используя данную формулу легко определить динамику параметров во время нагрева газа или его сжатия.
Наша программа позволяет рассчитать соотношение параметров идеального газа при их изменении. Для использования калькулятора требуется задать пять известных величин, после чего программа определит последнее неизвестное. Рассмотрим небольшой пример.
Пример использования калькулятора
Представим баллон газа объемом 15 л под давлением 120 кПа и при температуре –20 градусов Цельсия. Определим температуру газа, если баллон будет заменен на емкость объемом 10 л и давлением 150 кПа. На первый взгляд у нас есть все параметры, однако в газовых законах температура обязательно указывается в кельвинах, а не градусах. Для перевода температуры в систему Си достаточно прибавить к значению величину 273. Получаем, что температура газа составляет 253 К. Теперь вводим данные в соответствующие ячейки и смотрим на результат: конечная температура теперь равна 210 К или –63 градуса Цельсия. Очевидно, что газ подчинился приведенным выше законам и при уменьшении объема его температура также уменьшилась.
Заключение
Газовые законы — серьезная тема школьного курса физики, которую более подробно разбирают на первом году обучения в вузах. Комбинированный закон газа прост на первый взгляд, но обилие параметров может запутать школьника, а выведение пропорций и вовсе способно превратить задачу в ад. Для упрощения расчетов используйте наш онлайн-калькулятор, не забывая переводить все заданные параметры в систему СИ.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:
Примеры задач на уравнение Менделеева-Клапейрона
В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)
В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Теперь немного формул.
где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль
Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также
где n — число молей газа
И как нетрудно заметить, соотношение
есть величина постоянная для одного и того же количества моль газа.
И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.
Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.
Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры
Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры
Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.
Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.
Введение
Задача измерения параметров газовой смеси широко распространена в промышленности и торговле. Проблема получения достоверной информации при измерении параметров состояния газовой среды и её характеристик с помощью технических средств разрешается принятыми в стандартах методиками выполнения измерений (МВИ), например, при измерении расхода и количества газов с помощью стандартных сужающих устройств [1], или с помощью турбинных, ротационных и вихревых расходомеров и счётчиков [2].
Периодический газовый анализ позволяет установить соответствие между реальной анализируемой смесью и её моделью, по которой в МВИ учитываются физико-химические параметры газа: состав газовой смеси и плотность газа при стандартных условиях.
Также в МВИ учитываются теплофизические характеристики газа: плотность при рабочих условиях (давление и температура газа, при которых выполняют измерение его расхода или объёма), вязкость, фактор и коэффициент сжимаемости.
К измеряемым в реальном режиме времени параметрам состояния газа относятся: давление (перепад давлений), температура, плотность. Для измерения этих параметров применяются соответственно средства измерительной техники: манометры (дифманометры), термометры, плотномеры. Измерение плотности газовой среды допускается измерять прямым или косвенным методами измерения. Результаты как прямых, так и косвенных методов измерения зависят от погрешности средств измерения и методической погрешности. В рабочих условиях, сигналы измерительной информации могут быть подвержены влиянию значительного шума, среднее квадратичное отклонение которого может превышать инструментальную погрешность. В этом случае, актуальной задачей является эффективная фильтрация сигналов измерительной информации.
В данной статье рассматривается методика косвенного измерения плотности газа при рабочих и стандартных условиях c применением фильтра Калмана.
Математическая модель определения плотности газа
Обратимся к классике и вспомним уравнение состояния идеального газа [3]. Имеем:
1. Уравнение Менделеева-Клапейрона:
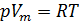 (1),
(1),
 — давление газа;
— давление газа;
 — молярный объём;
— молярный объём;
R — универсальная газовая постоянная,
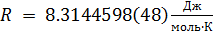 ;
;
T — абсолютная температура, T=273.16 К.
2. Два измеряемых параметра:
p – давление газа, Па
t – температура газа, °С.
Известно, что молярный объём  зависит от объёма газа V и количества молей газа
зависит от объёма газа V и количества молей газа 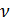 в этом объёме:
в этом объёме:
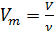 (2)
(2)
Также известно, что
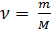 (3),
(3),
где: m – масса газа, M – молярная масса газа.
Учитывая (2) и (3) перепишем (1) в виде:
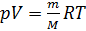 (4).
(4).
Как известно, плотность вещества
 равна:
равна:
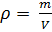 (5).
(5).
Из (4) и (5) выведем уравнение для плотности газа
 :
:
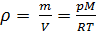 (6)
(6)
и введём обозначение параметра
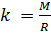 , который зависит от молярной массы газовой смеси:
, который зависит от молярной массы газовой смеси:
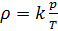 (7).
(7).
Если состав газовой смеси не меняется, то параметр k является константой.
Итак, для расчёта плотности газа необходимо рассчитать молярную массу газовой смеси.
Молярную массу смеси веществ определяем, как среднее арифметическое взвешенное молярной массы массовых долей, входящих в смесь индивидуальных веществ.
Примем известным состав веществ в газовой смеси – в воздухе, который состоит из:
- 23 % по весу из молекул кислорода

- 76 % по весу из молекул азота
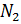
- 1 % по весу из атомов аргона
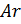
Молярные массы этих веществ воздуха будут соответственно равны:
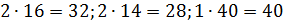 , г/моль.
, г/моль.
Вычисляем молярную массу воздуха, как среднее арифметическое взвешенное:
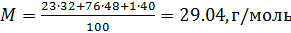
Теперь, зная значение константы
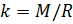 , мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений
, мы можем вычислить плотность воздуха по формуле (7) с учетом измеряемых значений
 и t:
и t:
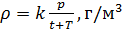
Приведение плотности газа к нормальным, стандартным условиям
Практически, измерения свойств газов проводят в различных физических условиях, и для обеспечения сопоставления между различными наборами данных должны быть установлены стандартные наборы условий [4].
Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.
Различные организации устанавливают свои стандартные условия, например: Международный союз чистой и прикладной химии (IUPAC), установил в области химии определение стандартной температуры и давления (STP): температура 0 °C (273.15 K), абсолютное давление 1 бар ( Па); Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP); Международная организация по стандартизации (ISO) устанавливает стандартные условия для природного газа (ISO 13443: 1996, подтверждённый в 2013 году): температура 15.00 °С и абсолютное давление 101.325 кПа.
Поэтому, в промышленности и торговле необходимо указывать стандартные условия для температуры и давления, относительно которых и проводить необходимые расчёты.
Плотность воздуха мы рассчитываем по уравнению (8) в рабочих условиях температуры и давления. В соответствии с (6) запишем уравнение для плотности воздуха в стандартных условиях: температура 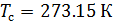 и абсолютное давление
и абсолютное давление 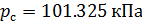 :
:
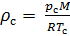 (9).
(9).
Делаем расчёт плотности воздуха, приведенной к стандартным условиям. Разделим уравнение (9) на уравнение (6) и запишем это отношение для 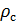 :
:
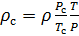 (10).
(10).
Подобным образом, получим уравнение для расчёта плотности воздуха, приведенной к нормальным условиям: температура 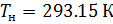 и абсолютное давление
и абсолютное давление
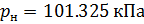 :
:
 (11).
(11).
В уравнениях (10) и (11) используем значения параметров воздуха  , T и P из уравнения (8), полученные в рабочих условиях.
, T и P из уравнения (8), полученные в рабочих условиях.
Реализация измерительного канала давления и температуры
Для решения многих задач получения информации, в зависимости от их сложности, удобно создавать прототип будущей системы на базе одной из микроконтроллерных платформ типа Arduino, Nucleo, Teensy, и др.
Что может быть проще? Давайте сделаем микроконтроллерную платформу для решения конкретной задачи – создание системы измерения давления и температуры, затрачивая меньше, возможно, средств, и используя все преимущества разработки программного обеспечения в среде Arduino Software (IDE).
Для этого, на аппаратном уровне, нам понадобятся компоненты:
- Arduino (Uno, …) – используем как программатор;
- микроконтроллер ATmega328P-PU – микроконтроллер будущей платформы;
- кварцевый резонатор на 16 МГц и пара керамических конденсаторов на 12-22 пФ каждый (по рекомендациям фирмы-изготовителя);
- тактовая кнопка на перезагрузку микроконтроллера и подтягивающий плюс питания к выводу RESET микроконтроллера резистор на 1 кОм;
- BMP180 — измерительный преобразователь температуры и давления с интерфейсом I2C;
- преобразователь интерфейсов TTL/USB;
- расходные материалы – провода, припой, монтажная плата, и др.
Принципиальная схема платформы, с учетом необходимых интерфейсов: стандартного последовательного интерфейса, I2C, и ничего более, представлена на рис. 1.
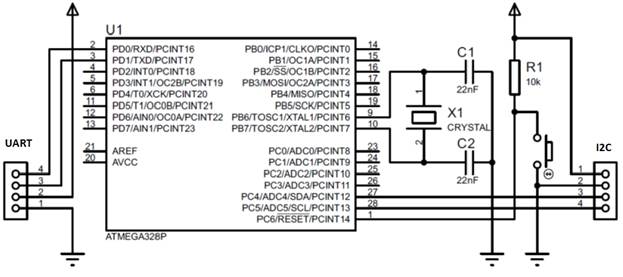
Рис. 1 — Принципиальная схема микроконтроллерной платформы для реализации системы измерения давления и температуры
Теперь рассмотрим этапы осуществления нашей задачи.
1. Прежде, нам нужен программатор. Подключаем Arduino (Uno, …) к компьютеру. В среде Arduno Software из меню по пути Файл->Примеры->11. ArdunoISP добираемся до программы программатора ArduinoISP, которую зашиваем в Arduino. Предварительно из меню Инструменты выбираем соответственно Плату, Процессор, Загрузчик, Порт. После Загрузки программы ArduinoISP в плату, наша Arduino превращается в программатор и готова к использованию по назначению. Для этого в среде Arduno Software в меню Инструменты выбираем пункт Программатор: “Arduino as ISP”.
2. Подключаем по интерфейсу SPI ведомый микроконтроллер ATmega328P к ведущему программатору Arduino (Uno, …), рис. 2. Следует заметить, что предварительно биты регистра Low Fuse Byte микроконтроллера ATmega328P были установлены в незапрограммированное состояние. Переходим в среду Arduno Software и из меню Инструменты выбираем пункт Записать Загрузчик. Прошиваем микроконтроллер ATmega328P.
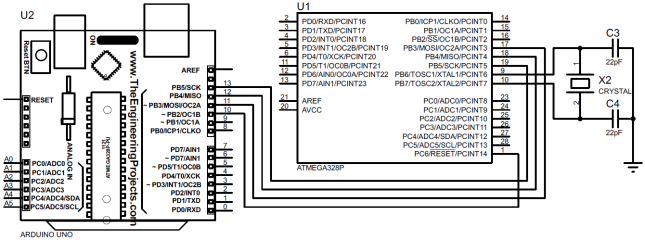
Рис. 2 – Схема подключения микроконтроллера к программатору
3. После успешной прошивки, микроконтроллер ATmega328P готов к установке на разработанную микроконтроллерную платформу (рис. 3), которую программируем также, как и полноценную Arduino (Uno, …). Программа опроса измерительного преобразователя давления и температуры представлена на листинге 1.

Рис. 3 Система измерения давления и температуры
Программа Python для фильтрации по каналам температуры и давления, и получение результатов
Программа Python методики определения плотности газа по результатам измерений давления и температуры представлена на листинге 2. Информация из измерительной системы выводится в реальном режиме времени.
Результаты расчёта представлены листингом и рис. 4, 5, 6.
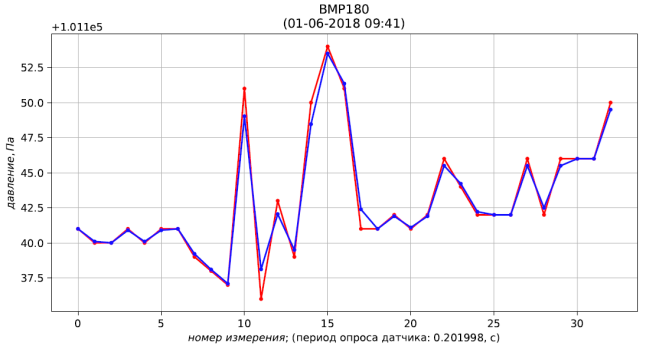
Рис. 4 – результаты измерения (красный) и фильтрации (синий) давления
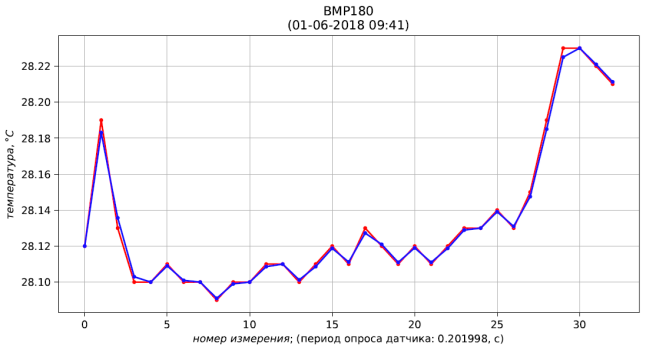
Рис. 5 – результаты измерения (красный) и фильтрации (синий) температуры
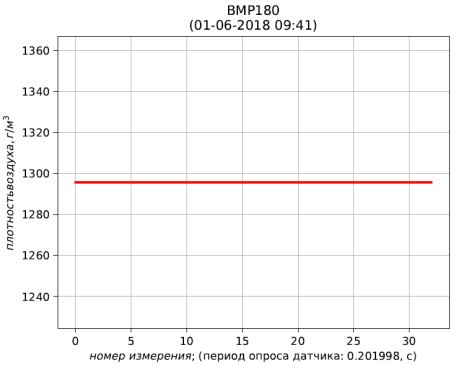
Рис. 6 – результаты расчёта плотности воздуха, приведенной к стандартным условиям (температура 273.15 К; абсолютное давление 101.325 кПа)
Выводы
Разработана методика определения плотности газа по результатам измерения давления и температуры с применением датчиков Arduino и программных средств Python.
Содержание:
- Свойства газов
- Давление газов
- Зависимость между объёмом и давлением газа. Закон Еойля — Мариотта
- Зависимость между плотностью газа и его давлением
- Зависимость объёма газа от температуры. Закон Гей-Люссака
- Зависимость давления газа от температуры. Закон Шарля
- Абсолютная шкала температур
- Зависимость между объёмом, давлением и температурой газа
- Физическая сущность понятия абсолютного нуля
- Изменение температуры газа при быстром расширении и сжатии
- Применение сжатых газов
Газ – это одно из трёх основных агрегатных состояний вещества, характеризующееся очень слабыми связями между составляющими его частицами (молекулами, атомами или ионами), а также их большой подвижностью. Частицы газа почти свободно и хаотически движутся в промежутках между столкновениями, во время которых происходит резкое изменение характера их движения.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Свойства газов
Главные свойства газов – это подвижность и хаотичное движение частиц, направление которых меняется при столкновении. Газ – одно из 4 агрегатных состояний веществ, которые на сегодняшний день известны науке.
Давление газов
Всякий газ производит давление на оболочку, внутри которой он находится.
Давление, производимое газом на стенки сосуда, объясняется ударами движущихся молекул.
При ударе о стенку молекулы газа отдают ей определённое количество движения; стенка испытывает при этом действие некоторой силы.
Удар каждой отдельной молекулы о стенку сосуда производит очень небольшое действие. Но молекул газа очень много, удары о стенки сосуда происходят беспрерывно, поэтому в результате получается значительное давление.
Хаотичность движения молекул приводит к тому, что давление газа одинаково во всех направлениях.
При нагревании давление газа увеличивается. Так как при этом число молекул газа не изменяется, то увеличение давления можно объяснить только тем, что удары молекул о стенки заключающего газ сосуда делаются при нагревании чаще и что каждый удар становится сильнее. Удары же могут стать чаще и сильнее, если увеличивается скорость движения молекул. Это подтверждается, как мы видели (гл. V), многочисленными опытами.
Зависимость между объёмом и давлением газа. Закон Еойля — Мариотта
Состояние газа определяется его объёмом, давлением и температурой. С изменением этих величин меняется и состояние газа. Мы будем рассматривать последовательно процессы, при которых одна из величин, характеризующих состояние газа, постоянна, а две другие меняются.
Изучим сначала такой процесс, при котором давление и объём газа изменяются, а температура остаётся постоянной. Такой процесс называется изотермическим 1.
1 От греч. слов: изос — равный, термос — тёплый.
Итак, рассмотрим, как изменяется давление данной массы газа при изменении его объёма, если температура газа не меняется.
Опыты, устанавливающие эту зависимость, можно произвести на приборе, три положения которого изображены на рисунке 134.

Рис. 134. Прибор для установления зависимости между объёмом и давлением газа (в трёх положениях).
В этом приборе стеклянная трубка А соединяется резиновой трубкой с другой стеклянной трубкой В. Трубка А вверху снабжена краном  обе трубки наполняются ртутью.
обе трубки наполняются ртутью.
Откроем кран  и установим трубку В так, чтобы уровень ртути в трубке А был, например, на середине трубки (положение I). Давление над ртутью в обеих трубках атмосферное; допустим, что оно равно 76 см рт. ст. Закроем теперь кран, отделив этим массу воздуха в трубке А от атмосферного воздуха. Таким образом, в этой стадии опыта мы будем иметь в трубке А определённую массу воздуха, находящегося под давлением p1 = 76 см рт. ст.
и установим трубку В так, чтобы уровень ртути в трубке А был, например, на середине трубки (положение I). Давление над ртутью в обеих трубках атмосферное; допустим, что оно равно 76 см рт. ст. Закроем теперь кран, отделив этим массу воздуха в трубке А от атмосферного воздуха. Таким образом, в этой стадии опыта мы будем иметь в трубке А определённую массу воздуха, находящегося под давлением p1 = 76 см рт. ст.
Поднимем теперь трубку В вверх на столько, чтобы объём воздуха в трубке А уменьшился вдвое (положение II). Уровень ртути в трубке В при этом значительно поднимется над уровнем в трубке А.
Рассмотрим теперь, чему будет равно давление воздуха в трубке А. Это давление уравновешивает атмосферное давление и давление всего столба ртути в трубке В, стоящего выше уровня n1 высота этого столба n1n оказывается равной 76 см. Таким образом, давление воздуха в трубке А уравновешивает не одну, как в первом случае, а две атмосферы (р2 = 2 am).
Значит, с уменьшением объёма данной массы газа в два раза давление его увеличивается в два раза. Если уменьшить объём газа в 1,5; 2,5; 3 раза, то соответственно в 1,5; 2,5; 3 раза увеличится его давление.
Опустим теперь трубку В так, чтобы масса воздуха в трубке А заняла вдвое больший объём (положение III). Уровень ртути в трубке А при этом понизится. Атмосферное давление теперь уравновешивает давление воздуха в трубке А и давление столба ртути от уровня n в трубке А до уровня в трубке В. Измерения показывают, что высота этого столба ртути равна 38 см. Давление, производимое воздухом в трубке А, найдём, вычтя из атмосферного давления давление столба ртути: р3 = 76 см—38 см = 38 см; следовательно, р3 = 0,5 am.
Итак, при увеличении объёма газа в два раза его давление уменьшается в два раза.
Перемещая трубку В в различные положения и отсчитывая каждый раз объём и давление воздуха в трубке А, найдём, что при уменьшении объёма исследуемой массы воздуха в некоторое число раз давление его увеличивается во столько же раз. Температура воздуха при всех опытах остаётся постоянной.
Опыты, проведённые с другими газами, дали те же результаты.
Изучая на опыте зависимость давления газа от его объёма, английский учёный Бойль (1627—1691) и французский учёный Мариотт (1620—1684) независимо один от другого открыли следующий закон.
Давление данной массы газа при неизменной температуре обратно пропорционально объёму газа.
Этот закон называется законом Бойля — Мариотта.
Выразим закон Бойля — Мариотта математически. Пусть температура некоторой массы газа постоянная и пусть:
V1 — объём газа при давлении р1,
V2 » » » » р2.
Согласно закону Бойля — Мариотта можно написать:

Из этой формулы следует, что:

Полученное равенство можно рассматривать как новое выражение закона Бойля — Мариотта.
Произведение объёма данной массы газа на его давление при неизменной температуре есть величина постоянная.
Изобразим графически изотермическое изменение состояния газа. Для этого по оси абсцисс будем откладывать значения объёмов газа, а по оси ординат соответствующие им значения давлений. Выберем масштаб так, чтобы начальные значения объёма и давления были равны 1. Тогда начальное состояние газа будет изображено точкой А (рис. 135). Если давление увеличится вдвое, объём уменьшится в два раза, состояние газа изобразится на графике точкой В. При уменьшении первоначального давления вдвое объём удвоится, получим точку С. Беря далее давления в три, четыре и т. д. раза больше или меньше начального, а объёмы соответственно в три, четыре и т. д. раза меньше или больше, получим ряд точек, изображающих различные состояния одной и той же массы газа при одинаковой температуре.

Рис. 135. График изотермического процесса.
Проведя через эти точки линию, получим кривую, которая называется изотермой.
Тщательными исследованиями установлено, что для реально существующих газов закон Бойля — Мариотта имеет лишь приближённое значение. Так, например, если произведение pV при 1 am равно единице, то при 2 am оно имеет следующие значения:
для воздуха ………………………0,99977
» водорода …………………….. 1,00026
» окиси углерода………………….. 0,99974
» двуокиси углерода………………… 0,99720
При очень больших давлениях (в сотни и тысячи атмосфер) закон Бойля — Мариотта становится совершенно неприменимым; в таких случаях зависимость между объёмом и давлением газа выражается более сложными уравнениями.
Зависимость между плотностью газа и его давлением
Плотность газа численно равна массе, заключённой в единице объёма.
Масса газа не меняется при его сжатии или расширении, но объём меняется; следовательно, меняется и плотность газа.
Пусть при постоянной температуре: D1 — плотность газа при объёме V1 и давлении p1 , a D2 — плотность газа при объёме V2 и давлении p2.
Если масса газа равна m, то можно написать:

откуда:

Но  на основании закона Бойля — Мариотта; поэтому
на основании закона Бойля — Мариотта; поэтому

При постоянной температуре плотность газа прямо пропорциональна его давлению.
Нетрудно понять справедливость этого вывода, исходя из молекулярно-кинетической теории. В самом деле, давление газа обусловлено ударами его молекул. Если объём газа уменьшится вдвое, то в новом объёме , плотность газа станет вдвое больше. Вдвое увеличится и число ударов молекул о стенки, т. е. давление газа возрастёт в два раза.
Зависимость объёма газа от температуры. Закон Гей-Люссака
Как и все тела, газы при нагревании расширяются, причём весьма заметно даже при незначительном нагревании. Это легко обнаружить на следующем простом опыте (рис. 136).

Рис. 136. Установка для наблюдения расширения газа при нагревании.
Колба А соединяется с расположенной горизонтально трубкой CD, которая укреплена вдоль шкалы. Внутри этой трубки находится небольшой столбик ртути. Достаточно к колбе прикоснуться рукой, как столбик ртути в трубке CD начнёт двигаться.
При охлаждении колбы столбик ртути перемещается влево, а при нагревании — вправо; следовательно, газ при охлаждении сжимается, а при нагревании расширяется. Зная объём колбы и диаметр трубки, можно измерить увеличение объёма газа.
Постепенно нагревая газ в колбе, можно установить, что при постоянном давлении изменение объёма данной массы газа пропорционально изменению температуры. Поэтому тепловое расширение газа, так же как и других тел, можно охарактеризовать при помощи коэффициента объёмного расширения.
Пусть при температуре 0°С объём газа равен V0 , а при температуре t объём Vt. Увеличение объёма, приходящееся на каждую единицу объёма, взятого при 0°С, при нагревании на один градус будет равно:

откуда:  (1)
(1)
Величина  входящая в писанные выше формулы, называется коэффициентом объёмного расширения газа.
входящая в писанные выше формулы, называется коэффициентом объёмного расширения газа.

Жозеф Луи Гей-Люссак (1778—1850)— один из выдающихся французских химиков и физиков. Он открыл ряд важных химических и физических законов, из которых в физике широко известен закон одинакового расширения газов и паров при одинаковом повышении температуры.
Французский учёный Гей-Люссак, исследуя на опыте тепловое расширение газов, открыл, что, коэффициент объёмного расширения у всех газов при постоянном давлении одинаков и численно равен 
В этом отношении расширение газов при нагревании отличается от расширения твёрдых и жидких тел, где, как мы видели (см. § 81 и 82), коэффициент объёмного расширения зависит от химического состава тел.
Положим в формуле (1): 
получим:  откуда следует, что при нагревании на 1° под постоянным давлением объём данной массы газа увеличивается на
откуда следует, что при нагревании на 1° под постоянным давлением объём данной массы газа увеличивается на  того объёма, который газ занимал при 0°С.
того объёма, который газ занимал при 0°С.
Этот закон получил название закона Гей-Люссака. Процессы, подобные рассмотренному, протекающие при постоянном давлении, называются изобарными1.
1 От греч. слов: изос — равный, барос — тяжесть, вес.
Формула (1) показывает, что объём газа при температуре t° равен произведению его объёма, взятого при 0°С, на двучлен объёмного расширения 
Пример. 1. Объём некоторой массы газа при 0°С равен 10 л. Найти объём его при t=273°С, если давление постоянно.
По условиям задачи нам известен объём газа при 0°С, т. е. V0 = 10 л; подставляя числовые данные задачи в формулу  найдем, что
найдем, что

Пример 2. При температуре 273°С объём некоторой массы газа равен 10 л. Чему будет равняться объём этого газа при температуре 546°С, если давление постоянно?
Нам известен объём газа при температуре 273°С; чтобы определить объём этого газа при t2 = 546°С, надо предварительно найти его объём при 0°.
Этот объём найдётся из равенства:

откуда:

Найдём теперь объём газа при 546°:

Зависимость давления газа от температуры. Закон Шарля
Нагревая газ в закрытом цилиндре, например в папиновом котле (рис. 136а), можно по манометру заметить, что давление газа увеличивается. Следя по термометру за повышением температуры, легко установить, что при постоянном объёме давление газа возрастает пропорционально повышению температуры.

Рис. 136а. При нагревании газа в закрытом цилиндре давление его повышается.
Аналогично тому, как для характеристики теплового расширения газов мы ввели коэффициент объёмного расширения, введём величину, характеризующую изменение давления газа при изменении его температуры.
Обозначим буквой р0 давление газа при 0°С, a pt — давление при t°. Увеличение давления, приходящееся на каждую единицу начального давления при нагревании на 1°С, будет равно:
 (1)
(1)
Величина  (греч. «гамма») называется термическим коэффициентом давления газа.
(греч. «гамма») называется термическим коэффициентом давления газа.
Измерения показывают, что величина термического коэффициента давления для всех
газов одинакова и равна 
Определяя из формулы (1) величину pt получим:
 (2)
(2)
Положим в формуле (2)  тогда
тогда 
Отсюда следует, что давление данной массы газа при нагревании на 1° при постоянном объеме увеличивается на  того давления, которым обладал газ при 0°C.
того давления, которым обладал газ при 0°C.
Этот закон называется законом Шарля, по имени французского учёного, открывшего его в 1787 г.
Из закона Шарля следует, что термический коэффициент давления газа  равен коэффициенту объёмного расширения
равен коэффициенту объёмного расширения  Это равенство вытекает из закона Бойля — Мариотта. Докажем это.
Это равенство вытекает из закона Бойля — Мариотта. Докажем это.
Пусть некоторая масса газа заключена в цилиндре под поршнем (рис. 137, а) и пусть температура её в этом начальном состоянии равна 0°, объём V0 и давление р0. Закрепим поршень АВ и нагреем газ до температуры t° (рис. 137, б); тогда давление газа увеличится и станет равным рt объём же его останется прежним.
По закону Шарля: 
Будем теперь газ нагревать от 0 до t° (рис. 137, в), предоставив поршню свободно перемещаться. Давление газа останется таким же, каким было в начальном его состоянии, т. е. р0 , объём же увеличится до Vt. По закону Гей-Люссака:


Рис. 137.
а) начальное состояние газа: 0°, V0, р0;
б) состояние газа, определяемое величинами: 
в) состояние газа, определяемое величинами: 
Итак, имеем: при температуре t° объём данной массы газа V0 и давление  при той же температуре: давление р0 и объём
при той же температуре: давление р0 и объём  По закону Бойля— Мариотта:
По закону Бойля— Мариотта:

После упрощения этого выражения получаем равенство:

Выразим сначала в виде таблицы, а потом графически зависимость давления газа от температуры. Для этого воспользуемся уравнением:


Рис. 138. График изменения давления газа от температуры.
Отложим по оси абсцисс в некотором условном масштабе температуры газа, а по оси ординат соответствующие этим температурам давления, взятые из написанной выше таблицы.
Соединяя на графике отмеченные точки, получим прямую LM (рис. 138), представляющую собой график зависимости давления газа от температуры при постоянном объёме.
Процесс изменения состояния газа, происходящий при неизменном объёме газа, называется изохорным 1 процессом, а линия LM, изображающая изменение давления газа при постоянном объеме в зависимости от температуры, называется изохорой.
1 От греч. слов: изос — разный, хорема — вместимость.
Пример 1. Давление газа при 0°С равно 780 мм рт. ст. Определить давление этого газа при температуре 273°С.
По формуле  найдем, что
найдем, что

Пример 2. Чему будет равно давление газа при температуре 546°, если давление его при температуре 273° равно 780 мм рт. cm.?
В этой задаче прежде всего надо определить давление газа при 0°С. По формуле  находим:
находим:

Теперь можно определить давление газа при t = 546°:

Законы Гей-Люссака и Шарля так же, как и закон Бойля — Мариотта, лишь приближённо отражают свойства газов. Это можно видеть хотя бы. из того факта, что для разных газов величины  и
и  несколько различаются между собой (см. таблицу).
несколько различаются между собой (см. таблицу).

Точные измерения показывают, что для каждого данного газа значения  и
и  получаются разные в зависимости от того, в каком температурном интервале и при каком давлении они определены. Однако эти различия очень незначительны, они учитываются лишь при весьма точных расчётах.
получаются разные в зависимости от того, в каком температурном интервале и при каком давлении они определены. Однако эти различия очень незначительны, они учитываются лишь при весьма точных расчётах.
Абсолютная шкала температур
Вернёмся ещё раз к графику изменения давления газа с температурой (рис. 138).
Продолжим прямую LM на этом графике до пересечения её с горизонтальной осью, по которой откладываются температуры газа, она пересечёт эту ось в точке K. Отрезок ОК будет изображать на этом графике такую температуру газа, при которой давление его равно нулю. Чему равна эта температура?
Обратимся к уравнению  Положим в этом уравнении pt = 0, т. е. напишем следующее равенство:
Положим в этом уравнении pt = 0, т. е. напишем следующее равенство:

Так как давление газа при 0°С не равно нулю  то из написанного равенства следует, что:
то из написанного равенства следует, что:

откуда:  или, так как
или, так как

Итак, давление газа равняется нулю при температуре —273°С.

Вильям Томсон (Кельвин) (1824— 1907) — выдающийся английский физик. Ему принадлежат важные открытия в области теории электричества и теплоты и изобретения, из которых наиболее значительным было усовершенствование телеграфной связи. Он ввёл в физику понятие об абсолютной температуре. Его именем названы градусы шкалы абсолютных температур — градусы Кельвина.
Английский учёный Вильям Томсон (Кельвин) предложил такую шкалу температур, при которой за нуль градусов принята температура — 273°. Эта шкала получила название абсолютной шкалы температур, или шкалы Кельвина, а нуль градусов этой шкалы, равный — 273°, называется абсолютным нулём температур.
В шкале Кельвина величина градуса та же, что и в стоградусной шкале.
Будем обозначать температуру по шкале Кельвина буквой Т.
При нормальном атмосферном давлении температура таяния льда по шкале Кельвина Т0 = 273°, температура же кипения воды T = 373°.
Всякая другая температура t° стоградусной шкалы связана с абсолютной температурой Т соотношениями:

Зависимость между объёмом, давлением и температурой газа
Объединённый закон газового состояния. Мы рассмотрели процессы, в которых одна из трёх величин, характеризующих состояние газа (объём, давление и температура), не меняется.
Вы видели, что если не меняется температура, то давление и объём газа связаны друг с другом законом Бойля —- Мариотта. При постоянном давлении объём газа изменяется с изменением температуры по закону Гей-Люссака, и, наконец, при постоянном объёме давление газа меняется с изменением температуры по закону Шарля.
Однако в природе часто имеют место процессы, когда одновременно меняются все три величины, характеризующие состояние газа. Установим теперь, какая связь существует между объёмом, давлением и температурой.
Пусть для двух каких-либо произвольных состояний некоторой массы газа эти величины будут:

Из этих состояний изменением величин р, V или t газ можно перевести в любые другие состояния. Будем, например, сохраняя постоянным давление, переводить газ из состояний 1) и 2) в состояния, при которых температура газа будет равна 0°С.
По закону Гей-Люссака объём газа V1 после уменьшения температуры от до 0° будет равен  объём V2, после уменьшения температуры от t2 до 0° будет
объём V2, после уменьшения температуры от t2 до 0° будет 
Новые состояния газа выразятся так:

В обоих этих состояниях температура газа одинакова, поэтому на основании закона Бойля — Мариотта можно написать:
 (1)
(1)
Так как величины р, V, t, характеризующие состояние рассматриваемого газа и обозначенные индексами 1 и 2, выбраны были нами произвольно, то равенство (1) справедливо для любых состояний этого газа. Поэтому можно утверждать, что:
 (2)
(2)
Для данной массы газа произведение давления газа на его объём, делённое на двучлен объёмного расширения, есть величина постоянная.
Выведенная нами зависимость между объёмом, давлением и температурой газа называется объединённым законом газового состояния, а равенство (1) или (2) — уравнением состояния газа.
Уравнение состояния газа можно упростить, введя в него вместо температуры t по стоградусной шкале температуру Т по абсолютной шкале температур. Для этого преобразуем уравнение:

Введя в него значение  получим:
получим:

что после сокращения на 273 даст:

Но  и
и  ; следовательно, можно написать:
; следовательно, можно написать:

Это означает, что для данной массы газа произведение давления на объём, делённое на абсолютную температуру, постоянно при всех температурах: 
В частности, если при температуре Т = 273° объём газа равен V0 и давление его р0 , то можно написать:

Физическая сущность понятия абсолютного нуля
Мы уже отмечали, что реальные газы лишь приближённо следуют законам Гей-Люссака, Шарля и Бойля — Мариотта. Однако можно представить себе газ, для которого эти законы выполнялись бы в точности. Молекулы такого газа можно представить себе в виде упругих шариков исчезающе малого объёма, взаимодействие между которыми осуществляется только через их столкновения друг с другом. В физике такой газ принято называть идеальным газом.
Из уравнения  следует, что при t = —273°, т. е. при абсолютном нуле, давление газа равно нулю. Но ведь давление газа есть результат ударов движущихся молекул о стенки сосуда. Следовательно, при температуре абсолютного нуля должно прекратиться тепловое движение молекул идеального газа.
следует, что при t = —273°, т. е. при абсолютном нуле, давление газа равно нулю. Но ведь давление газа есть результат ударов движущихся молекул о стенки сосуда. Следовательно, при температуре абсолютного нуля должно прекратиться тепловое движение молекул идеального газа.
Опыт показывает, что при малых давлениях свойства реальных газов очень близки к свойствам идеального газа. Следовательно, при приближении к температуре абсолютного нуля должно прекратиться тепловое движение молекул и реального газа. Этот вывод относится не только к газам, но и к твёрдым и жидким телам.
Физикой установлено, что такое состояние вещества недостижимо, но к нему можно подойти очень близко. В настоящее время достигнута температура, которая выше абсолютного нуля всего на несколько стотысячных долей градуса.
Изменение температуры газа при быстром расширении и сжатии
Опыты показывают, что при быстром сжатии температура газа повышается, а при быстром расширении понижается.
Увеличение температуры газа при сжатии можно показать на следующем простом опыте. Возьмём толстостенный цилиндрический стеклянный сосуд, внутри которого может двигаться поршень (рис. 139). При быстром сжатии воздух в сосуде сильно нагревается, и легко воспламеняющееся вещество (например, ватка, смоченная эфиром), положенное на дно сосуда, вспыхивает. Такого рода явление используется, например, в двигателях внутреннего сгорания —дизелях: при сжатии воздуха в цилиндре двигателя горючая смесь, введённая в цилиндр, нагревается до температуры воспламенения (работа двигателя описана в § 131).

Рис. 139. При быстром сжатии воздух в цилиндре сильно нагревается и легко воспламеняющееся вещество вспыхивает.
При быстром же расширении газа температура его понижается. Это можно наблюдать на следующем опыте. Будем накачивать воздух в прочную закрытую пробкой стеклянную банку, содержащую пары воды. При достижении определённого давления пробка выскочит; при этом воздух, расширяясь, совершит работу и охладится, вследствие чего водяной пар превратится в туман (рис. 140).

Рис. 140. Сжатый в сосуде воздух, выбрасывая пробку, расширяется. Совершая при этом работу, он охлаждается, вследствие чего водяной пар в сосуде превращается в туман.
Понижение температуры при быстром расширении газа используется для получения сжиженных газов; об этом будет рассказано в § 122.
Изменение температуры тела, как было установлено в § 71, связано с изменением внутренней энергии тела. Так как при быстром сжатии температура газа повышается, то внутренняя энергия его при этом увеличивается. Увеличение внутренней энергии газа происходит в результате работы, совершённой при его сжатии. Расширяясь же, газ совершает работу; при этом внутренняя энергия его уменьшается, и если расширение происходит быстро, то температура газа, как мы видели в наших опытах, понижается.
Процесс, происходящий в теле без теплообмена с окружающими его другими телами, называется адиабатным процессом.
Все быстро протекающие процессы практически могут считаться адиабатными.
Применение сжатых газов
Многие сжатые газы в настоящее время находят широкое применение в технике.
Сжатый воздух, например, применяется в работе различных пневматических инструментов: отбойных молотков, заклёпочных молотков, в разбрызгивателях краски и др.
На рисунке 141 показана схема устройства отбойного молотка. Сжатый воздух подаётся в молоток по шлангу М. Золотники Z, аналогичные применяемым в паровых машинах, направляют его поочерёдно то в заднюю, то в переднюю часть цилиндра. Поэтому воздух давит на поршень Р то с одной, то с другой стороны, что вызывает быстрое возвратно-поступательное движение поршня и пики молотка В. Последняя наносит быстро следующие друг за другом удары, внедряется в уголь и откалывает куски его от массива.

Рис. 141. Схема устройства отбойного молотка.
Существуют также пескоструйные аппараты, которые дают сильную струю воздуха, смешанную с песком. Эти аппараты применяются, например, для очистки стен. Сейчас нередко можно видеть работу специальных аппаратов, применяемых для окраски стен, где краска распыляется сжатым воздухом. Сжатым воздухом открываются двери вагонов метро и троллейбусов. Сжатый воздух используется в работе тормозов на транспорте. Схематическое устройство одного из видов пневматического тормоза железнодорожного вагона изображено на рисунке 142.
Компрессор подаёт воздух по магистрали в стальной резервуар А. Поршень В тормозного цилиндра оказывается под одинаковым давлением справа и слева; поэтому соединённая с ним тормозная колодка D отжата от колеса. Если открыть тормозной кран М, то находящийся в магистрали под давлением воздух устремится в атмосферу; клапан К захлопнется, и, таким образом, стальной резервуар изолируется от магистрали. Теперь давление на поршень В справа станет больше, чем давление слева, вследствие чего тормозная колодка прижмётся к ободу колеса. Если теперь кран М закрыть и снова подать в магистраль сжатый воздух, то восстановится первоначальное положение.

Рис. 142. Схема устройства железнодорожного пневматического тормоза.
В технике применяется не только сжатый воздух, но и некоторые другие газы, так, например, водород, ацетилен и кислород применяются при газовой сварке; аммиак используется в холодильном деле. Чтобы газы было удобно перевозить, их помещают в прочные стальные баллоны, накачивая до давления 60—200 am.

Рис. 142а. Внешний вид мощного компрессора.
Сжатие газов осуществляется с помощью мощных нагнетательных насосов — компрессоров.
На рисунке 143, а, б дана схема работы компрессора.
Компрессор состоит из цилиндра с поршнем и двумя клапанами; один из них входной, другой выходной. При движении поршня вниз (рис. 143, б) открывается входной клапан и в цилиндр поступает воздух из помещения; при движении поршня вверх (рис. 143, а) входной клапан закрывается, вошедший воздух сжимается поршнем и через выходной клапан поступает в стальной баллон для хранения сжатого газа.
Существуют так называемые многоступенчатые компрессоры, в которых газ последовательно
сжимается в трёх или четырёх цилиндрах. Такие компрессоры позволяют получить газ, сжатый до давления в тысячи атмосфер. На рисунке 142а изображён внешний вид одного из типов многоступенчатых компрессоров.

Рис. 143, а, б. Схема работы компрессора.
Услуги по физике:
- Заказать физику
- Заказать контрольную работу по физике
- Помощь по физике
Лекции по физике:
- Физические величины и их измерение
- Основные законы механики
- Прямолинейное равномерное движение
- Прямолинейное равнопеременное движение
- Сила
- Масса
- Взаимодействия тел
- Механическая энергия
- Импульс
- Вращение твердого тела
- Криволинейное движение тел
- Колебания
- Колебания и волны
- Механические колебания и волны
- Бегущая волна
- Стоячие волны
- Акустика
- Звук
- Звук и ультразвук
- Движение жидкости и газа
- Молекулярно-кинетическая теория
- Молекулярно-кинетическая теория строения вещества
- Молекулярно – кинетическая теория газообразного состояния вещества
- Теплота и работа
- Температура и теплота
- Термодинамические процессы
- Идеальный газ
- Уравнение состояния идеального газа
- Изменение внутренней энергии
- Переход вещества из жидкого состояния в газообразное и обратно
- Кипение, свойства паров, критическое состояние вещества
- Водяной пар в атмосфере
- Плавление и кристаллизация
- Тепловое расширение тел
- Энтропия
- Процессы перехода из одного агрегатного состояния в другое
- Тепловое расширение твердых и жидких тел
- Свойства жидкостей
- Свойства твёрдых тел
- Изменение агрегатного состояния вещества
- Тепловые двигатели
- Электрическое поле
- Постоянный ток
- Переменный ток
- Магнитное поле
- Электромагнитное поле
- Электромагнитное излучение
- Электрический заряд (Закон Кулона)
- Электрический ток в металлах
- Электрический ток в электролитах
- Электрический ток в газах и в вакууме
- Электрический ток в полупроводниках
- Электромагнитная индукция
- Работа, мощность и тепловое действие электрического тока
- Термоэлектрические явления
- Распространение электромагнитных волн
- Интерференционные явления
- Рассеяние
- Дифракция рентгеновских лучей на кристалле
- Двойное лучепреломление
- Магнитное поле и электромагнитная индукция
- Электромагнитные колебания и волны
- Природа света
- Распространение света
- Отражение и преломление света
- Оптические приборы и зрение
- Волновые свойства света
- Действия света
- Линзы и получение изображений с помощью линз
- Оптические приборы и глаз
- Фотометрия
- Излучение и спектры
- Квантовые свойства излучения
- Специальная теория относительности в физике
- Теория относительности
- Квантовая теория и природа поля
- Строение и свойства вещества
- Физика атомного ядра
- Строение атома
Молекулы всех газов при одной и той же
температуре обладают одинаковой средней
кинетической энергией. Причем давление
газа при данной температуре зависит
только от числа молекул в единице объема
газа. В основе объяснений физических
свойств газов и законов газового
состояния лежит кинетическая теория.
Большинство законов газового состояния
было выведено для идеального газа.
Идеальным называют газ, в котором
молекулы рассматриваются как материальные
точки, обладающие массой, но не имеющие
при этом объёма, между которыми отсутствуют
силы взаимодействия.
При
больших объёмах и малых давлениях, когда
расстояние между молекулами во много
раз больше собственных размеров молекул,
а также при высоких температурах, когда
интенсивность хаотического движения
молекул велика и поэтому молекулы слабо
взаимодействуют между собой, складываются
условия, при которых реальный газ можно
с некоторым приближением считать
идеальным.
Закон Бойля — Мариотта.
Английский ученый
Бойль и независимо от него несколько
позднее французский физик Мариотт на
основании экспериментов пришли к выводу
о том, что объем данной
массы газа и его давление находятся в
обратно пропорциональной зависимости.
Эта зависимость между давлением и
объемом газа при постоянной температуре
выражается формулой:
![]()
, (1)
где V1
и Р1
– объем и абсолютное давление газа до
их изменения; V2
и Р2 –
то же, после изменения.
Из данной формулы можно получить
следующие математические выражения:
![]()
, (2)
или
![]()
при
![]()
. (3)
Из последней формулы следует,
что произведение
давления данной массы газа на его объем
постоянно, если температура газа не
меняется.
Закон
имеет практическое применение в газовом
хозяйстве. Он позволяет определять
объем газа при изменении его давленная
и давление газа при изменении его объема
при условии, что температура газа
остаётся постоянной.
Чем больше при постоянной
температуре увеличивается объем газа,
тем меньше становится его плотность.
Зависимость между
объёмом газа и его плотностью при
постоянной температуре выражается
формулой
![]()
, (4)
где V1
и V2
– объемы, занимаемые газом; ρ1
и ρ2
– плотности газа, соответствующие этим
объемам.
Если в формуле (1) заменим отношение
объемов газа отношением их плотностей,
то на основании формулы (4) можно получить.
![]()
или
![]()
(5)
Из формулы (5) можно сделать
вывод, что при одной
и той же температуре плотности газов
прямо пропорциональны давлениям, под
которым находятся эти газы, т.е. плотность
газа (при постоянной температуре) будет
тем больше, чем больше будет его давление.
Пример.
Объем газа при давлении 760 мм.рт.ст. и
при температуре 0°С составляет 300 м3.
Какой объем займет этот газ при абсолютном
давлении, равном 1520 мм.рт.ст. и при той
же температуре?
760 мм.рт.ст. = 101 320 Па = 101,3 кПа;
1520 мм.рт.ст. = 202 630 Па = 202,6 кПа.
Подставляем заданные
значения V1,
Р1,
и Р2
в формулу (2):
Р1 =
101,3 кПа; V1
= 300 м3;
Р2 =
202,6 кПа;
101,3 х 300 = 202,6 V2,
откуда V2
= (101,3
х 300)/202,6 = 150 м3.
Закон Гей-Люссака.
Французский химик Гей-Люссак впервые
установил зависимость объема газа от
температуры при постоянном давлении.
Сущность этой зависимости заключается
в том, что при постоянном
давлении относительное изменение объема
данной массы газа прямо пропорционально
изменению температуры.
Математически эта зависимость между
объемом и температурой газа при постоянном
давлении записывается следующим образом:
![]()
, (6)
где V
– объем газа, м3;
Т – абсолютная
температура, К.
Из формулы (6) следует, что
если определенный
объем газа нагревать при постоянном
давлении, то его объем изменится во
столько раз, во сколько раз изменится
его абсолютная температура.
Многочисленные опыты
показывают, что при нагревании газов
на 1 градус при постоянном давлении их
объем увеличивается на постоянную
величину, равную 1/273,2 первоначального
их объема. Эта величина называется
термическим
коэффициентом объемного расширения
и обозначается α
= 1/273,2 град-1.
С учетом этого закон
Гей-Люссака можно сформулировать так:
объем данной массы
газа при постоянном давлении увеличивается
линейно при повышении температуры
![]()
; (7)
![]()
; (8)
![]()
, (9)
где Vt
и V0
– объемы газа при
конечной и начальной температурах, м3;
t
и Т – начальная и конечная температуры,
оС,
К; α – термический коэффициент объёмного
расширения.
Из формулы (9) следует, что
объем газа при постоянном
давлении прямо пропорционален его
абсолютной температуре.
Закон Шарля.
Согласно закону Шарля,
давление данной массы
газа при постоянном объеме прямо
пропорционально абсолютной температуре.
Из этого закона следует, что отношение
давлений массы газа при постоянном
объеме равно отношению его абсолютных
температур. Закон
выражается следующей формулой:
![]()
или
![]()
, (10)
где Р1
и Р2
– абсолютные давления; Т1
и
Т2
– абсолютные температуры
газа, К.
Из формулы (10) можно сделать вывод, что
при постоянном объеме давление газа
при нагревании увеличивается во столько
раз, во сколько раз увеличивается его
абсолютная температура.
Пример 1.
При температуре газа 27°С его давление
равно 4 МПа (40 кгс/см2).
Каково будет избыточное давление этого
газа при температуре 47°С?
Начальная абсолютная
температура газа равна:
![]()
,
конечная абсолютная
температура газа равна:
![]()
.
Атмосферное давление примем
равным 0,1 МПа (1 кгс/см2),
тогда абсолютное давление газа до
нагревания будет:
![]()
.
Искомое абсолютное давление
газа Р2
по формуле (10) равное:
![]()
.
Следовательно, избыточное давление
газа после нагревания его до 47°С равно:
![]()
.
Пример 2.
Сжатый газ в баллоне при температуре
7°С имел избыточное давление 0,9МПа. После
нагревания давление в баллоне повысилось
до 1,1 МПа. До какой температуры был нагрет
газ?
Начальная абсолютная
температура газа:
![]()
.
Начальное абсолютное
давление газа:
![]()
.
Конечное абсолютное давление
газа:
![]()
.
Из формулы (10) после
преобразования ее относительно
неизвестной Т2
получаем:
![]()
.
Следовательно, газ в баллоне был нагрет
до температуры 63°С.
Закон
Авогадро. Итальянский
ученый Амадео Авогадро выразил
предположение, что различные
газы, занимающие одинаковые объёмы при
равных условиях (одинаковые давление
и температура), содержат одинаковое
число молекул.
Это число для одной
грамм-молекулы (1 моль) любого газа
составляет около N
= 6,064 х
1023
и называется числом Авогадро. В дальнейшем
было экспериментально установлено, что
1 грамм-молекула любого газа при нормальных
условиях занимает объем 22,4л.
В Международной системе
единиц производной является величина,
в 1000 раз большая моля, она называется
киломоль и
обозначается кмоль.
1 кмоль любого газа
при нормальных условиях (0°С и 101,3 кПа)
занимает объем 22,4 м3.
Зная эту величину, можно определить
плотность любого газа по формуле
![]()
, (11)
где М —
масса 1 кмоля газа, кг.
Пример 1.
Определить плотность метана при
нормальных условиях (ОоС
и 101,3 кПа):
![]()
.
Пример 2. В баллоне находится 100 кг
жидкого этана. Определить объем паров
этана, полученных при его полном испарении
в нормальных условиях.
Решение. Сначала определяют число
киломолей этана:
п = 100 : 30,07 = 3,33 (здесь 30,07 –
молекулярная масса этана).
Зная, что 1 киломоль этана при испарении,
т.е. в газообразном состоянии, занимает
объем 22,4 м3, находят объем паров
этана от испарения всего его количества:
V = 22,4 х
3,33 = 74,63 м3.
Уравнение Клапейрона —
Менделеева.
При одновременном изменении объема,
давления и температуры газа справедливы
законы и Бойля — Мариотта и Гей-Люссака.
Французский ученый Клапейрон пришел к
выводу о существовании для газов
некоторой универсальной функции. Русский
ученый Д.И. Менделеев вывел в более общем
виде уравнение состояния идеальных
газов, объединив уравнения законов
Бойля — Мариотта и Гей-Люссака в одно
общее математическое уравнение идеального
газа, которое называется уравнением
Клайперона—Менделеева:
![]()
. (12)
Величина
![]()
обозначается буквой “R”
называется газовой постоянной. Подставляя
обозначение газовой постоянной в формулу
(12), получаем выражение:
![]()
или
![]()
. (13)
Это
уравнение закона газового состояния
связывает все три основных параметра
данного количества газа: объем, абсолютное
давление и абсолютную температуру, и
оно относится к 1 молю газа.
Из уравнения следует, что
для определенного
количества газа произведение его объема
на абсолютное давление равно произведению
газовой постоянной на абсолютную
температуру газа. Числовое
значение газовой постоянной зависит
от величин параметров, входящих в
уравнение (13).
В Международной системе универсальная
газовая постоянная для 1 кмоля равна:
![]()
,
где 101325 – нормальное давление, Па.
Уравнением Клапейрона —
Менделеева часто пользуются при пересчете
характеристик газа. Формулы (14) и (15),
предназначенные для пересчета параметров,
характеризующих состояние газа в
нормальных и стандартных условиях,
получены путем соответствующих,
преобразований выражения
.
![]()
, (14)
![]()
, (15)
где VН Vст
– объём газа при нормальных и стандартных
условиях, м3; Vt
– объём газа при реальных условиях, м3;
Pt –
давление газа при реальных условиях,
Па; Р – давление газа при нормальных и
стандартных условиях (101325 Па).
Закон Дальтона.
Смеси газов (паров),
близких по своим свойствам к идеальным,
характеризуются аддитивностью парциальных
давлений. Аддитивность
(от лат. additivus
– прибавляемый), свойство объекта, по
которому величина всего объекта равна
сумме величин частей объекта при любом
разбиении. Так, масса тела равна сумме
масс его частей.
Парциальным давлением
компонента ρi
газовой смеси называется то давление,
которое этот компонент оказывал бы,
если бы из смеси удалить все другие
компоненты при сохранении первоначальных
объема и температуры системы. Закон
аддитивности записывается следующим
образом:
![]()
(16)
где π — общее давление смеси
газов (паров). Из уравнения
![]()
следует, что
![]()
(17)
Подставив это выражение в уравнение
(17), получим
![]()
(18)
Следовательно
![]()
(19)
или
![]()
(20)
т.е. парциальное
давление компонента равно давлению
системы, умноженному на мольную долю
этого компонента в газовой фазе.
Пример. Известен молярный состав
смеси газов, %: метан – 90, этан – 5, пропан
– 2, азот – 2, бутаны – 1. Смесь находится
под давлением 12 МПа. Требуется определить
парциальное давление компонентов смеси.
Решение. Пользуясь уравнением, вычисляют
парциальное давление компонентов:
pC1
= 0,9*12 = 10,8 МПа;
pC2
= 0,05*12 = 0,6 МПа;
pC3
= 0,02*12 = 0,24 МПа;
pC4
= 0,02*12 = 0,24 МПа;
pC5
= 0,01*12 = 0,12 МПа.
Законы реальных газов.
При повышении давления
объем реального газа становится меньше,
чем идеального. Это
обстоятельство учитывают введением
соответствующих поправок в законы
идеальных газов.
Так,
уравнение состояния реального газа
можно записать в виде:
![]()
(21)
где z
— коэффициент сжимаемости, являющийся
функцией приведенного давления Рпр
= P/Pкр
и приведенной
температуры Tпр
= T/Ткр;
Ркр
и Ткр
— критические давление и температура
(табличные значения).
Давление насыщенных
паров. Пары жидкости
могут быть насыщенными и ненасыщенными.
Насыщенным называется
пар, находящийся в равновесии с жидкостью.
Чем выше температура, тем выше давление,
при котором находится данная равновесная
система. Для насыщенных паров существует
однозначная зависимость между давлением
паров и температурой Р
= f(T).
Ненасыщенными (перегретыми)
парами называют пары, которые при данных
температуре и давлении образуют
однофазную систему.
Жидкая фаза отсутствует.
Известно, что жидкость
начинает кипеть при такой температуре,
при которой давление её насыщенных
паров Р
становится равным внешнему давлению
π. Давление насыщенных паров определяют
по табличным данным или эмпирическим
уравнениям (ур-е Антуана, Киреева).
Для определения ДНП
нефтепродуктов, представляющих собой
сложные смеси углеводородов различных
классов, предложены графики и формулы
(Кокса, Ашворта, Вильсона, BWR
и др.)
Закон Рауля. Этот закон
устанавливает зависимость между
парциальным давлением компонента,
входящего в состав раствора, его молярной
концентрацией в жидкой смеси Х
и упругостью пара того же чистого
компонента при заданной температуре
Q.
Парциальное давление компонента в
жидкой смеси равно его молярной
концентрации, умноженной на упругость
его паров в чистом виде при данной
температуре:
![]()
(22)
где р – парциальное давление
компонента в растворе.
По закону Рауля, сумма парциальных
давлений всех компонентов равна общему
давлению над смесью или общей упругости
паров смеси:
![]()
![]()
где
ХnQn
– молярная концентрация и упругость
паров компонента соответственно.
Пример. Жидкая смесь состоит из
этана –60%, пропана –25 % и изобутана
–15 % (молярные доли). Требуется определить
общее давление системы при температуре
100С.
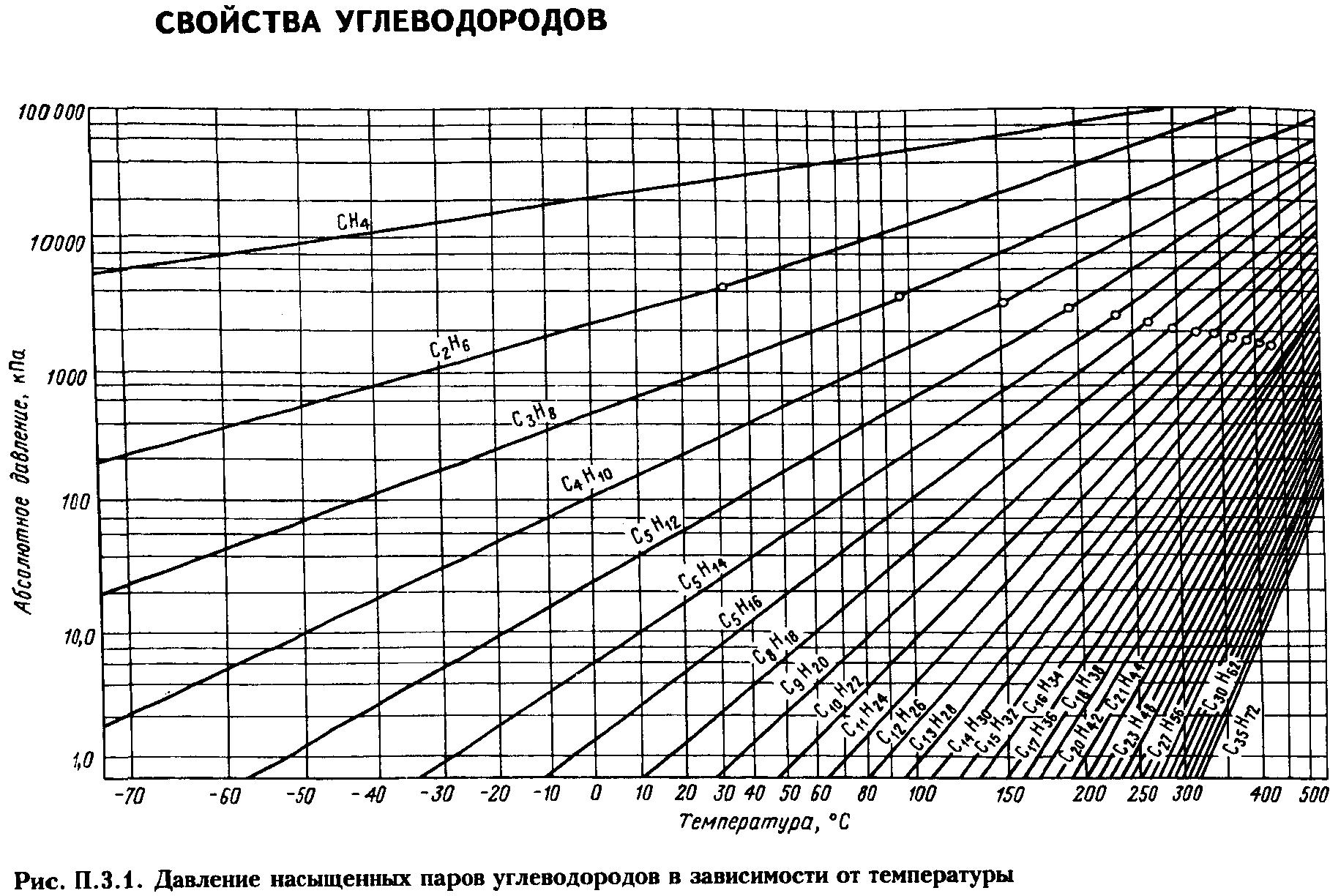
Решение. Сначала из рис. 2.1 (график Кокса)
находим давление насыщенных паров
компонентов в чистом виде при 10°С:
QC2
= 0,326 МПа; QC3
= 0,63 МПа; QC4
= 0,16 МПа
Затем по уравнению определим общее
давление системы:
![]()
Данные этого примера показывают, что
если бы указанная смесь транспортировалась
в жидком виде при 10°С, то трубопровод
работал под давлением 2,14 МПа.
Важным выводом, вытекающим из закона
Рауля, является то, что высококипящие
компоненты имеют низкую упругость,
содержатся в паровой фазе в малых
количествах; следовательно, их
основная доля находится в жидкой фазе.
Что касается низкокипящих компонентов,
обладающих высокой упругостью, то они
легко переходят в газовую фазу. На этом
положении основана работа многих
установок по частичной стабилизации
газового конденсата при выветривании
– ступенчатом снижении давления смеси
с одновременным ее расширением.

23
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Плотность – физическое свойство газа
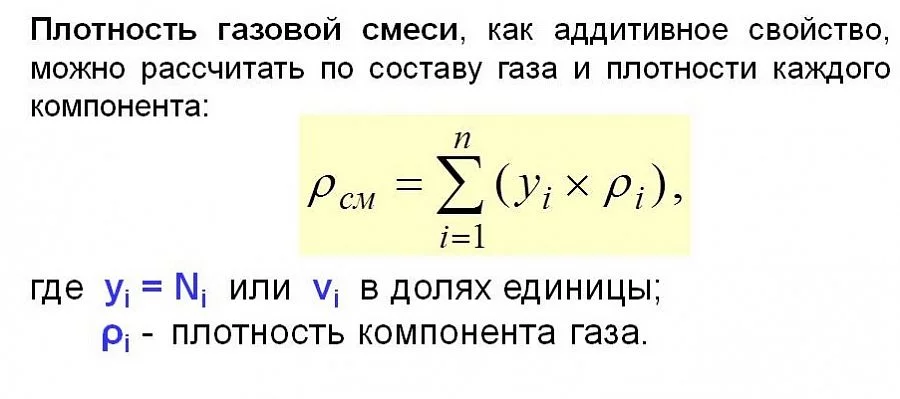
Плотность газа r вычисляют по формуле ( по ГОСТ 30319.1-96)
r = т/V.
Плотность определяют с помощью плотномеров любого типа (пикнометрических, ареометрических, вибрационных, акустических, радиационных и др.) или косвенным методом (измерением параметров состояния среды, определения ее состава и проведения расчета).
В зависимости от технико-экономической целесообразности плотность контролируемых сред допускается рассчитывать:
- вручную,
- с помощью таблиц и графиков,
- с применением вычислительных машин;
- частично или полностью автоматизированных устройств.
Плотность газа в идеально газовом состоянии определяют по известным значениям давления р и температуры Т по формуле
rи = 103 × M × p/(R × T).
За молярную массу М принимают массу одного киломоля вещества в килограммах.
Молярную массу определяют по формуле
![]() ,
,
где Аj – масса килограмм-атома j-го элемента, входящего в состав молекулы;
пj – количество атомов j-го элемента молекулы.
3.2.2 Плотность реального газа (далее – газ) определяют с учетом фактора сжимаемости газа z по формуле
![]() .
.
Плотность газа при стандартных условиях определяется при р = рc и Т = Тc т.е. по соотношению
![]() .
.
