Как найти плотность графа

Как найти плотность графа

Пло́тный граф — граф, в котором число рёбер E близко к максимально возможному у полного графа с числом вершин V:

{displaystyle E={frac {V(V-1)}{2}}.}

Граф, имеющий малое число рёбер, принято называть разреженным графом.

Вообще говоря, разница между разреженным и плотным графом условна и зависит от контекста.

Для неориентированного простого графа (рёберная)[1] плотность графа с числом вершин V определяется как отношение числа его рёбер E к числу рёбер полного графа:

{displaystyle D={frac {2E}{V,(V-1)}}}.

Максимальное число рёбер равно {displaystyle E={frac {V(V-1)}{2}},} так что максимальная плотность графа равна 1 (для полных графов) и минимальная равна 0 — для несвязанного графа[2].

Верхняя плотность[править | править код]

Верхняя плотность — это расширение понятия плотности графа с конечных графов на бесконечные. Интуитивно понятно, что бесконечный граф имеет произвольно большие конечные подграфы с любой плотностью, меньшей верхней плотности, и не имеет произвольно больших конечных подграфов с плотностью, большей верхней плотности. Формально, верхняя плотность графа G — это нижняя грань таких значений α, что конечные подграфы графа G с плотностью больше α имеют ограниченный порядок. Используя теорему Эрдёша — Стоуна[en] можно показать, что верхняя плотность может быть только 1 или одним из значений последовательности 0, 1/2, 2/3, 3/4, 4/5, … n/(n + 1), … (см, например, Дистель. Упражнения к главе 7[1]).

Разреженные и тугие графы[править | править код]

Штрейну[3] и Теран[4]
определяют граф как (k,l)-разреженный, если любой непустой подграф с n вершинами имеет максимум kn − l рёбер, и как (k,l)-тугой, если он (k,l)-разреженный и имеет в точности kn − l рёбер. Таким образом деревья в точности (1,1)-тугие графы, леса — в точности (1,1)-разреженные графы, а графы с древесностью k — в точности (k,k)-разреженные графы. Псевдолеса — это в точности (1,0)-разреженные графы, а Ламановы графы, появляющиеся в теории жёсткости[en], это в точности (2,3)-тугие графы.

Другие семейства графов также могут быть описаны подобным образом. Например, из того, что любой планарный граф с n вершинами имеет максимум 3n — 6 ребра, и что любой подграф планарного графа является планарным вытекает, что планарные графы являются (3,6)-разреженными графами. Однако не всякий (3,6)-разреженный граф будет планарным. Аналогично, внешнепланарные графы являются (2,3)-разреженными и планарные двудольные графы являются (2,4)-разреженными.

Штрейну и Теран показали, что проверка является ли граф (k,l)-разреженным, может быть выполнена за полиномиальное время.

Разреженные и плотные классы графов[править | править код]

Оссона и Нешетрил[5] полагают, что при делении на разреженные/плотные графы необходимо рассматривать бесконечные классы графов, а не отдельных представителей. Они определили местами плотные классы графов как классы, для которых существует такой порог t, что любой полный граф появляется как t-подраздел в подграфе графов класса. И наоборот, если такой порог не существует, класс называется нигде не плотным. Свойства деления на местами плотные/нигде не плотные обсуждается в статье Оссона и Нешетрил[6].

Примечания[править | править код]

  1. ↑ 1 2
    Рейнгард Дистель. Теория графов. — Новосибирск: Издательство института математики, 2002. — ISBN 5-86134-101-X.
  2. ↑
    Thomas F. Coleman, Jorge J. Moré. Estimation of sparse Jacobian matrices and graph coloring Problems // SIAM Journal on Numerical Analysis. — 1983. — Т. 20, вып. 1. — С. 187—209. — doi:10.1137/0720013.
  3. ↑ Audrey Lee, Ileana Streinu. Pebble game algorithms and sparse graphs // Discrete Mathematics. — 2008. — Т. 308, вып. 8. — С. 1425—1437. — doi:10.1016/j.disc.2007.07.104.
  4. ↑ I. Streinu, L. Theran. Sparse hypergraphs and pebble game algorithms // European Journal of Combinatorics. — 2009. — Т. 30, вып. 8. — С. 1944—1964. — doi:10.1016/j.ejc.2008.12.018. — arXiv:math/0703921.
  5. ↑ Patrice Ossona de Mendez, Jaroslav Nešetřil. European Congress of Mathematics. — European Mathematical Society, 2010. — С. 135—165.
  6. ↑ Jaroslav Nešetřil, Patrice Ossona de Mendez. Sparsity: Graphs, Structures, and Algorithms. — Heidelberg: Springer, 2012. — Т. 28. — ISBN 978-3-642-27874-7. — doi:10.1007/978-3-642-27875-4.

Литература[править | править код]

  • Paul E. Black, Sparse graph Архивная копия от 16 декабря 2008 на Wayback Machine, from Dictionary of Algorithms and Data Structures, Paul E. Black (ed.), NIST. Retrieved on 29 September 2005.
  • Preiss. Data Structures and Algorithms with Object-Oriented Design Patterns in C++. — John Wiley & Sons, 1998. — ISBN 0-471-24134-2.
Источник

В кластерном
анализе, при информационном поиске и
других практических задачах используется
понятие плотности графа.

Кластер
– (англ. пучок,
группа)
наименьший участок жесткого или
флоппи-диска (дискета); при фрагментации
задействованные (несущие информацию)
и свободные кластеры все более
перемешиваются, что отрицательно
сказывается на быстродействии компьютера;
для упорядочения распределения кластера
используются программа – дефрагментация.

Плотностью
графа

называется максимальная мощность
носителя полного подграфа К
графа G
и обозначается

:


.

Другими словами,
максимальное число попарно смежных
вершин графа G
является плотностью этого графа.

Следовательно,
для определения плотности

графа G
необходимо выделить в графе G
все полные подграфы.

Алгоритм выделения полных подграфов

1. Сопоставляем
корню строящегося дерева заданный граф
G
.

2. Фиксируем
в графе вершину


с максимальной
степенью,
сопоставив ее концу дуги, исходящей из
корня. Строим исходящие из корня дуги,
число которых равно

(

мощность
носителя неокрестности вершины v0
). Конец каждого из этих дуг взаимно
однозначно сопоставляем вершине
неокрестности

.

3. Каждый конец

построенных дуг взвешиваем окрестностью

вершины

графа, сопоставленного рассматриваемому
корню.

4. Считаем
конец

построенного яруса корнем нового дерева.

5. Устанавливаем,
взвешена ли вершина

символом Ø . Если “нет”, то переходим
к п.2, если “да” – то к п.6.

6. Каждая ветвь
построенного дерева однозначно определяет
полный подграф заданного графа G
.

Закон
поглощения. Если
в k
– ом ярусе дерева вершины vi
и vj
смежны, поддерево с корнем vi
построено и если в поддереве с корнем
vj
появляется вершина vi
, то соответствующая ветвь не строится.

Пример.
Определить
плотность

графа G
(рис. 5.10).

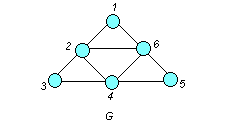
Рис. 5.10

□ Используя
алгоритм выделения полных подграфов,
построим искомое дерево (рис. 5.11).

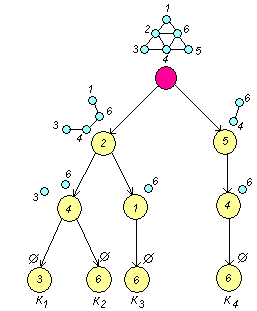
Рис. 5.11

Здесь Ki
– полные подграфы. Видно, что мощность
носителей всех подграфов равна трем,
значит

Каждое множество
состоит из попарно смежных вершин.
■

§ 6. Раскраска графа

К построению
раскрасок графов сводится целый ряд
практических задач, например, задачи
составления расписаний, распределения
оборудования, проектирования некоторых
технических изделий.

Раскраской
вершин графа

называется разбиение носителя V
графа G
на подмножества, при котором каждое
подмножество Vi
не содержит ни одной пары смежных
вершин.

Каждому
подмножеству сопоставляется цвет, в
который окрашивают элементы этого
подмножества.

Хроматическим
числом

графа G
называется минимальное число п
(число красок), для которого граф имеет
п
– раскраску.

Если

=
п
, то граф называется п
– хроматическим .

Если

(т –
число красок и раскраска удовлетворяет
определению), то граф называется т
– раскрашиваемым .

1 – хроматический
граф – это пустой граф.

Теорема 1.
Граф является
2 – хроматическим тогда и только тогда,
когда он не содержит циклов нечетной
длины.

Двудольный
граф – 2-хроматический граф.

Любое дерево
– 2-хроматический граф.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Экспресс-анализ метрических параметров графов

Время на прочтение
11 мин

Количество просмотров 3.9K

«А лохматость у меня повысилась.»

Итак, у нас на руках есть граф. Часто анализ графа сводят к его визуализации, поскольку «глаз — лучший инструмент». Не отрицая полезности вывода графа как картинки, отметим все же, что не все свойства графа можно увидеть. Некоторые надо считать.

Можно взять готовый пакет для работы с графами (например, NetworkX) и воспользоваться уже реализованными в нем функциями. Некоторые параметры графов имеют исключительно комбинаторный характер, и поэтому не подходят для графов с дробными значениями связей. Более универсальными характеристиками являются те, которые имеют метрическую основу. Далее мы приведем несколько таких параметров, способы их расчета и примеры использования.

Общие замечания

Арность

Параметр графа — это функция, которая возвращает действительное число. Данная функция может зависеть от аргументов. Количество аргументов функции называется арностью. Соответственно, параметры графа тоже характеризуются арностью (или рангом). В качестве аргументов выступают вершины графа.

Параметры 0-й арности характеризуют сам граф в целом, часто такие параметры называют инвариантами. Существуют инварианты, которые позволяют сравнивать между собой разные графы независимо от количества их вершин.

Параметры 1-й арности (1-го ранга, одинарные) характеризуют вершины графа. Наиболее известным из них является степень вершины — суммарное количество ее связей (в направленных графах входящие и исходящие степени будут разными). Другой известной характеристикой вершин является центральность, причем существуют разные центральности. Центральности можно считать разновидностью степеней вершин, адаптированных для оценки центра/периферии графа. Если у вас есть граф сотрудников вашей компании, то ключевые сотрудники скорее всего будут иметь наибольшее значение центральности.

Бинарные параметры зависят от двух вершин. Связь между вершинами — это бинарный параметр графа. На основе матрицы смежности можно сформировать пары вершин с наибольшей связью — это интересный параметр.

Ну и так далее. Можно рассчитать для графа и тернарные характеристики (3-го ранга), значение которых зависит от трех вершин.

Двойственность

Максимальная арность параметров равна количеству вершин графа. Но когда арность превышает половину от общего количества вершин вступает в силу принцип двойственности. Пусть граф имеет

$n$ вершин. Тогда дополнительной арностью для параметра

$k$-ой арности является

$(n - k)$-я арность. Поскольку вместо того, чтоб указывать, какие аргументы (вершины графа) используются для получения значения параметра, можно указать те, которые не используются. Это и порождает дополнительную арность.

Если параметр имеет максимальную арность (используются все вершины графа), то это эквивалентно дополнительной 0-й арности. Такой параметр характеризует весь граф целиком (а не подмножество его вершин). Если арность параметра на 1 меньше максимальной

$(n-1)$, то дополнительная арность равна 1. Такой параметр можно рассматривать как свойство вершин. Однако надо иметь в виду, что смысл значения параметра при этом меняется на противоположный. Например, связность всех вершин графа, кроме одной, можно трактовать как несвязность данной вершины.

Параметры близости и дальности

Рассматриваем ненаправленные графы, величина связей между вершинами которых может быть произвольным действительным числом (обычно положительным). Метрические параметры графа характеризуют либо некую близость, либо дальность вершин графа. Считаем, что связи графа заданы матрицей смежности, которую обозначим как

$C^{ij}$.

Связность и остовное число

Величина близости связана со степенью связи вершин, — чем более вершины связаны, тем они ближе. Количественную оценку степени связи множества вершин назовем связностью. Данный параметр может иметь арность от 2 до

$n$. Связность двух вершин — это величина связи между ними, задается его матрицей смежности графа. Связность 3-х вершин можно рассчитать на основе 2-связности:

$C^{abc} = C^{ab} C^{bc} + C^{ab} C^{ac} + C^{bc} C^{ac} quad (1)$

Связность всех

$n$ вершин графа называется его остовным числом

$tau(G)$. Комбинаторная интерпретация остовного числа — это количество остовных деревьев, которые можно построить на связях графа. В соответствии с матричной теоремой о деревьях остовное число можно рассчитать как определитель минора лапласиана графа. Если с какой-либо вершиной графа нет связи (это означает наличие в графе нескольких компонент), то остовное число графа (его общая связность) равно нулю.

В соответствии с принципом двойственности дополнительная арность остовного числа графа равна нулю, поэтому остовное число можно считать характеристикой всего графа.

Отсюда также следует, что связность подмножества вершин графа равна остовному числу подграфа, построенного на данном подмножестве вершин. Например, приведенная выше формула для 3-х вершин — это явное выражение остовного числа графа из 3-х вершин.

Наконец отметим также, что остовное число можно связать обратно пропорционально квадрату объема симплекса, построенного на вершинах графа. Чем больше связность — тем меньше объем:

$tau(G) = (l! vol)^{-2} quad (2)$

Здесь

$l = n-1$ — мерность пространства графа из

$n$ вершин.

Резистивная метрика

Дальность (расстояние, дистанция) является обратным понятием близости, но это не просто обратная величина связности. Как уже отмечалось в предыдущей статье, между любыми вершинами существует резистивная дистанция, даже если эти вершины напрямую не связаны.

Способ расчета матрицы резистивных дистанций

Определим матричное преобразование дистанции над произвольной матрицей

$X$ как

$D(X)_{ij} = X_{ii} + X_{jj} - X_{ij} - X_{ji} $

Матрица резистивных дистанций

$R$ может быть получена несколькими способами.
1) Можно использовать псевдообращение лапласиана графа и получить матрицу Грина:

$Gamma = L^{-1}$, после чего преобразование дистанции над матрицей Грина даст резистивную матрицу:

$R = D(Gamma)$. Минус данного способа в необходимости использовании алгоритма псевдообращения (поскольку лапласиан — вырожденная матрица).

2) Можно использовать обращение минора лапласиана и получить фундаментальную матрицу:

$F = (L^{(i)})^{-1}$. Преобразование дистанции над мажором фундаментальной матрицы также даст резистивную матрицу:

$R = D(F*)$. Мажор здесь означает добавление элемента (который удалили для получения минора лапласиана) в базисное множество фундаментальной матрицы. Плюс данного способа — в использовании обычного матричного обращения.

Резистивная метрика может иметь различную арность — от двух до максимальной. Резистивная дистанция (эффективное сопротивление) является бинарным параметром, поскольку для определения значения резистивной дистанции надо задать две вершины. Значение резистивной дистанции эквивалентно квадрату линейного расстояния (квадрансу). Но помимо геометрической резистивная дистанция имеет также комбинаторную трактовку. Ее значение в простых графах отражает относительное изменение остовного числа графа

$tau(G)$ при добавлении (или удалении) связи между данными вершинами:

$R_{ab} = Delta_{ab} tau / tau quad (3)$

Значение числителя

$Delta_{ab} tau$ равно детерминанту минора лапласиана, из которого удалены вершины

$a, b$ (двойственность — удаляем две вершины из множества, а не извлекаем).

Резистивной метрике 3-ей арности (тристанция?) соответствует квадрат двойной площади треугольника:

$R_{abc} = (2S_{abc})^2$. Для ее получения можно детерминант минора лапласиана, из которого удалены три вершины, разделить на остовное число графа. Также как и для 3-связности существует выражение 3-дальности через резистивные дистанции. Приведем для справки:

$4 R_{abc} = (R_{ab} + R_{bc} + R_{ac})^2 - 2(R_{ab}^2 + R_{bc}^2 + R_{abc}^2)$

Параметры описанной сферы

Поскольку граф можно трактовать как базис пространства, то геометрические характеристики данного пространства можно использовать для определения параметров графа. Известно, что вокруг невырожденного симплекса произвольного порядка всегда можно описать сферу. Такая сфера характеризуется: 1) положением центра и 2) радиусом. Положение центра задается барицентрическими координатами

$s^i$ относительно вершин симплекса, квадрат радиуса

$r$ — числом.

Параметры сферы имеют помимо геометрической комбинаторную интерпретацию. Более подробно рассмотрены здесь.

Остовная степень и центральность

Обратимся к одинарным (унарным) параметрам, — то есть к характеристикам вершин.

Как уже отмечалось, любой граф можно разложить на сумму деревьев (остовов). В каждом таком дереве вершина исходного графа может иметь различную степень. Тогда можно сложить степени вершин по всем деревьям графа и получить среднюю остовную степень вершин, обозначим ее как

$e^i$ (обычные степени вершин графа принято обозначать через

$d^i$, degree). Оказывается, что координаты центра описанной сферы

$s^i$ и средняя остовная степень связаны между собой соотношением:

$s^i = 1^i - e^i /2 quad (4) $

Данное выражение связывает геометрию с комбинаторикой. Видим, что координаты центра описанной сферы можно получить, просто считая степени вершин деревьев, на которые можно разложить граф.

С точки зрения прикладного анализа удобнее оперировать с центральностями вершин. Значения центральности можно трактовать как близость (или дальность) положения вершины относительно некоего центра графа. Центральность самых удаленных вершин должна быть нулевой. Из этого требования, а также из свойства барицентрических координат

$sum_i s^i = 1$ вытекает следующее определение центральности (для того, чтобы отличать ее от других, назовем ее остовной);

$cr^i = e^i - 1 = 1 - 2 s^i quad (5) $

Достоинство остовной центральности в том, что ее можно рассчитать на основе стандартных матричных операций. Приведем для справки соответствующие формулы:

$cr^i = diag(R_{ik} C^{kj} - I_i^j) = sum^j(R circ C)_i^j - 1 quad (5')$

Здесь

$C$ — матрица смежности графа,

$R$ — матрица резистивных дистанций (сопротивлений),

$circ$ — обозначает адамарово (поточечное) произведение матриц.

На основе остовной центральности можно выделить центральные вершины графа и его периферию. Если значение центральности вершины больше 1, то она относится к центру. Если меньше — к периферии.

К сожалению в пакете networkX расчет остовной центральности не реализован, но зато в нем есть несколько других центральностей, которые тоже можно использовать.

На рисунке показаны для сравнения две центральности для графа из Википедии. Слева a) — остовная центральность вершин, справа b) — betweenness centrality. Значения приведены к целым числам.

Целые значения остовной центральности интерпретируются просто — это разность (превышение) между суммой степеней вершины по всем остовам графа и общим количеством остовов. Рассмотрим, например, фиолетовую вершину. Поскольку она конечная, то ее степень во всех остовах равна 1. Поэтому общая сумма ее степеней совпадает с количеством остовов, в итоге получаем для нее нулевую центральность.
Немного странно, что алгоритм betweenness centrality дает также нулевое значение для красной вершины. Визуально очевидно, что положения красной и фиолетовой вершин совсем не равноправны.

Норма, связность и плотность графа

Размер описанной сферы характеризует граф в целом. Поскольку по определению все вершины графа принадлежат сфере, то ее диаметр задает максимально возможное значение резистивных дистанций (а, значит, и эффективных сопротивлений) между вершинами графа. Величину квадрата радиуса сферы назовем резистивной нормой графа

$r(G)$.

В отличие от остовного числа, которое имеет мультипликативный характер, норма графов аддитивна. Это проявляется, например, в операции сочленения графов (соединение в вершине). Норма результирующего графа равна сумме исходных графов, а остовное число — произведению.

Поскольку норма любого графа независимо от его порядка всегда является «квадратом расстояния», то нормы можно использовать чтобы сравнивать между собой графы разного порядка.

Однако в качестве топологической характеристики значение резистивной нормы графа не подходит. При увеличении величины связей в k раз его резистивная норма уменьшается во столько же раз, хотя очевидно, что топология (структура связей) при этом не изменилась.

Конструируем параметры плотности и разреженности графа

Для того, чтобы на основании нормы определить топологическую характеристику, необходимо умножить ее на величину какой-либо связности графа. В качестве такой связности подойдет средняя степень его вершин

$d(G)$.

Умножая резистивную норму на связность графа получаем некий безразмерный параметр, который назовем индексом разреженности

$spar(G)$:

$ spar(G) = r(G) d(G) quad (6) $

Величину, обратную данному индексу, назовем индексом компактности (плотности):

$ dens(G) = 1/spar(G) quad (7) $

Но это еще не все. Хорошо бы привязать введенные нами индексы к какому-то стандарту, например, к полному графу. Тогда мы бы могли сказать, насколько отличается плотность (или разреженность) от полного графа. Для этого введем понятие несмещенных оценок. Несмещенная оценка получается умножением инварианта на фактор

$n/(n-1)$ (подобный трюк есть в статистике при определении дисперсии). Несмещенные оценки пометим звездочкой:

$ r*(G) = r(G) n/(n-1), quad d*(G) = d(G) n/(n-1) (8) $

Тогда несмещенная оценка разреженности получается из обычной умножением на квадрат фактора — следствие определения (6):

$ spar*(G) = spar*(G) n^2/(n-1)^2 quad (9) $

Наконец-то мы добрались до финального выражения.

В полном графе

$K_n$ несмещенные индексы разреженности и компактности равны 1 — это предельные значения данных параметров. Из этого следует, что плотность (компактность) всех остальных графов будет меньше, чем плотность полного графа, а разреженность соответственно больше.

Например, несмещенная оценка плотности приведенного выше графа из Википедии равна 0.495. Данный граф примерно в два раза менее плотен, чем полный граф.

Спектральный и кластерный анализ

Особняком стоит анализ графов на основе спектров его матриц. В качестве матрицы обычно используется либо матрица смежности, либо лапласиан. Среди прочего спектр лапласиана используют для поиска кластеров вершин в графе, то есть выделения обособленных (слабо связанных) групп — этому посвящено большое количество работ.

Здесь нет возможности сильно вдаваться в подробности (да тут и не подходящее место для этого). Но считаем нужным отметить следующее для тех, кто будет использовать спектральный анализ для своих графов.

Обычно для поиска кластеров берут слой спектра лапласиана графа с наименьшим весом (наименьшим собственным значением) и формируют кластеры на основе близости значений соответствующего собственного вектора (вектор Фидлера). Но на практике (для графов с различными по величине связями) значение минимального собственного числа будет плохо обусловленным, — зависит от погрешностей данных. Да и вообще большинство слоев спектра обычно «плохо звенит», — направление таких слоев сформировано относительно небольшим числом вершин графа (это те, компоненты которых отличны от нуля в данном слое).

Поэтому для кластеризации надо сначала определить подходящие слои спектра. Такими слоями являются слои с наибольшей поляризацией вершин. Компоненты собственных векторов таких слоев должны быть заметно отличны от нуля (по абсолютному значению). Сами вершины делятся на кластеры по знаку компоненты. Соответственно для одного слоя получим два возможных кластера вершин. Если слоев два, то можно найти 4 кластера и т.д. При этом следует учитывать величину собственного числа слоя — оно определяет его мощность.

Сервис для анализа связности букв на основе корпуса слов

Чтобы разбавить унылую теорию веселой практикой, мы опубликовали сервис, который выполняет экспресс-анализ связности букв русского языка на основе заданного текста. Буквы связаны между собой неявным образом посредством слов, которые они образуют. На основании текстового файла сервис строит граф связности букв и выводить некоторые параметры из тех, которые описаны выше.

Используя данный сервис, можно выяснить, как меняются связи букв со временем. Мы сравнили графы букв, полученные по двум сказкам Пушкина «Сказка о мертвой царевне…» и «Сказка о царе Салтане», и более современное произведение Леонида Филатова «Сказ про Федота-стрельца».

Полученные центральности букв близки к общей частотности букв русского языка. Но заметны некоторые исторические особенности. Например, видно, что буква «ф» во времена Пушкина только народилась, — в «Сказке о мертвой царевне…» она вообще не встречается, а в «Сказке о царе Салтане» — только в единственном слове «флот».

Интересно, что значения центральностей букв связаны с их делением на кластеры (группы). Кластерный анализ текстов сказок (на основе спектра лапласиана графа букв) показал, что группы букв просто разбивают множество букв по степени их центральности. При этом существуют три основные группы (слоя) (показаны слои «по Филатову»):

Основная: [о, е, а, т, н, р, и, с, л, д*]
Промежуточная: [у, ь, к, в*, м, п, б, я]
Редкая: [ы, з, г, й, ч, ш, х, ж, ю, ц, ф, щ, э, ъ]

Внутри группы буквы отсортированы по степени убывания остовной центральности. Буквы основной группы можно отнести к центру (их центральности > 1), а промежуточной и редкой (центральность < 0.5) — к периферии.

Буквы «д» и «в» — беглые. За прошедшее время они поменялись местами. Роль буквы «д» повысилась, она перешла из промежуточного слоя в основной. А значимость «в» наоборот — понизилась. У Пушкина она была в основной группе, у Филатова — в промежуточной.

Наиболее связанные пары букв тоже известны. Вот первая десятка пар по степени убывания связи:

[е, н], [о, т], [е, т], [а, н], [а, к], [о, н], [а, р], [о, р], [а, л], [о, д]

Напомним, что граф ненаправленный, поэтому положение буквы внутри пары не имеет значения: [е, н] = [н, е]. Связность пары [о, д] в два раза меньше связности [е, н].

Отметим, что одна буква в парах данного списка всегда гласная, а другая согласная. Первая пара с двумя гласными находится на 11-м месте — это пара [е, о], а первая пара с двумя согласными — на 25-м: [с, т]. Отсюда ясно, что триплеты (три буквы) максимальной связности (см. формулу (1)) будут включать в себя буквы «е» и «о». Вот первые триплеты максимальной связности:

[ето], [оне], [неа], [ато], [нет], [рот], [сто], [она], [тон], [ора], [ока], [вот], [сет],…

От связности 3-й арности перейдем к 0-й и рассмотрим значение плотности/разреженности графа букв. Напомним, что минимальную разреженность (максимальную плотность) имеет полный граф. Все остальные графы намного более разрежены. Анализ показывает, что в современной сказке о Федоте разреженность равна примерно 39, в сказке о Салтане — 112, а в сказке о мертвой царевне — 222. Скорее всего более высокая плотность букв в сказке о Федоте объясняется ее большим объемом, то есть там просто больше разных слов и соответственно больше связей между разными буквами, которых нет у Пушкина.

Конечно, этот экспресс-анализ не претендует на широкие обобщения, поскольку выполнен на базе всего лишь трех текстов. Если взять более широкий корпус, то выводы могут быть другими.

Связность букв — лишь пример возможного анализа графа. Вы можете провести подобный анализ для своей компании на основании собственных данных.

Благодарю Сергея Аверкиева (averkij) за помощь в подготовке и публикации сервиса.

Источник

Содержание

  1. § 5. Плотность графа
  2. Алгоритм выделения полных подграфов
  3. § 6. Раскраска графа
  4. Раздел 1. Математическая логика
  5. Тема 1. Логика высказываний
  6. Тема 2. Булевы функции
  7. Тема 3. Логика предикатов
  8. Тема 4. Метод резолюций
  9. Раздел 2. Теория графов
  10. Тема 5. Раскраски
  11. §1. Хроматическое число
  12. §2. Оценки хроматического числа

§ 5. Плотность графа

В кластерном анализе, при информационном поиске и других практических задачах используется понятие плотности графа.

Кластер – (англ. пучок, группа) наименьший участок жесткого или флоппи-диска (дискета); при фрагментации задействованные (несущие информацию) и свободные кластеры все более перемешиваются, что отрицательно сказывается на быстродействии компьютера; для упорядочения распределения кластера используются программа – дефрагментация.

Плотностью графа 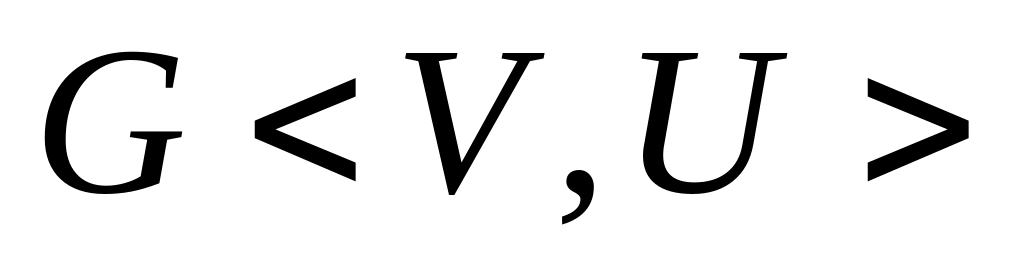называется максимальная мощность носителя полного подграфа К графа G и обозначается :

.

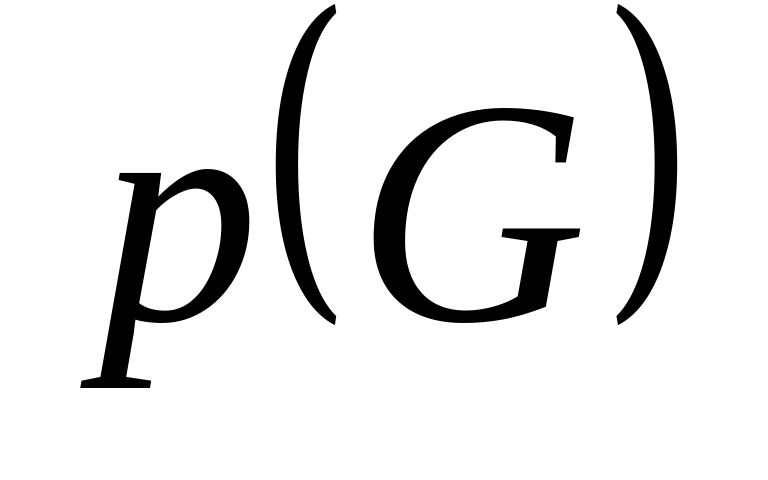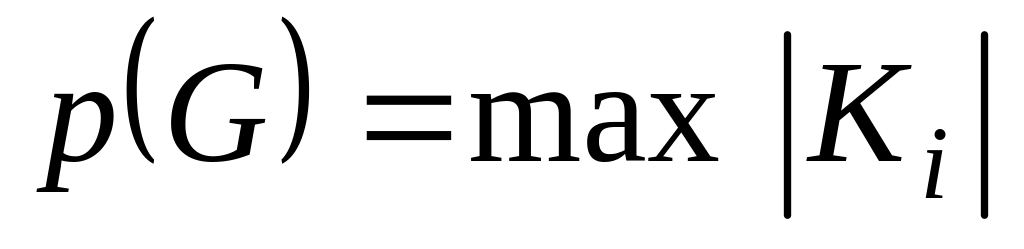Другими словами, максимальное число попарно смежных вершин графа G является плотностью этого графа.

Следовательно, для определения плотности графа G необходимо выделить в графе G все полные подграфы.

Алгоритм выделения полных подграфов

1. Сопоставляем корню строящегося дерева заданный граф G .

2. Фиксируем в графе вершину с максимальной степенью, сопоставив ее концу дуги, исходящей из корня. Строим исходящие из корня дуги, число которых равно 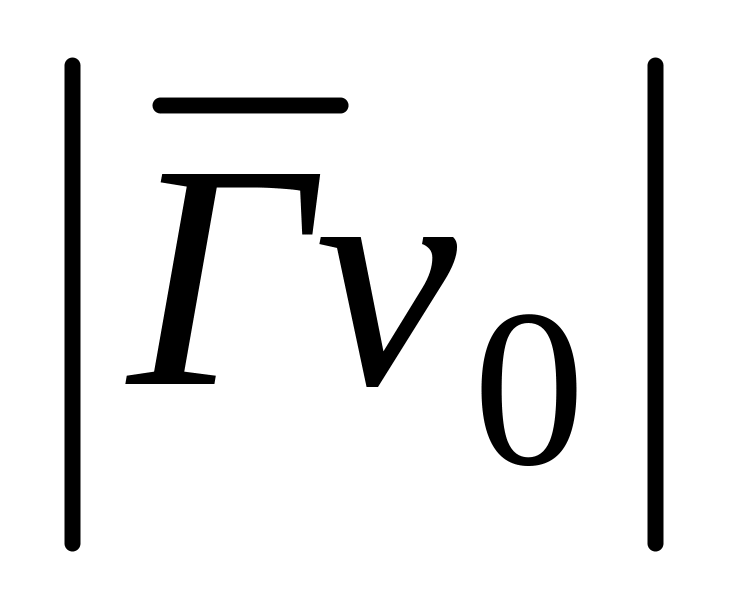( 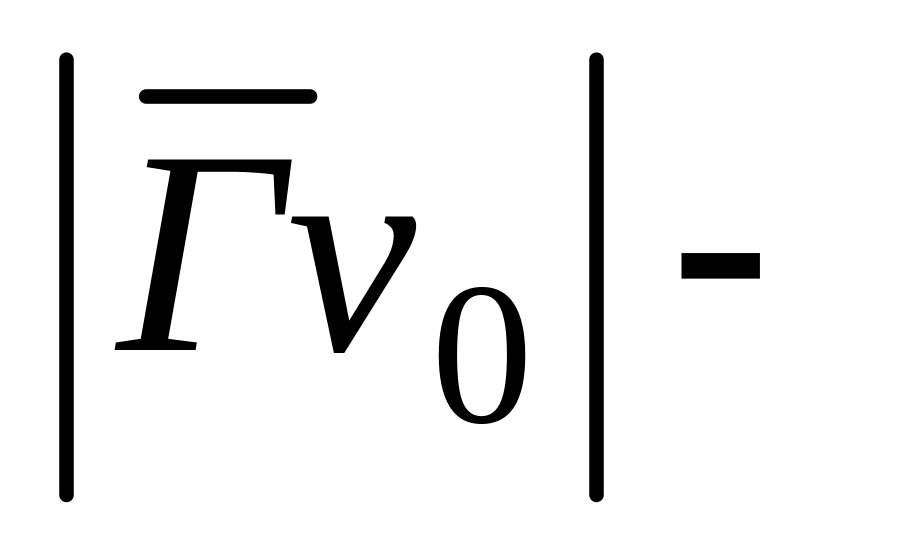мощность носителя неокрестности вершины v0 ). Конец каждого из этих дуг взаимно однозначно сопоставляем вершине неокрестности .

3. Каждый конец построенных дуг взвешиваем окрестностью 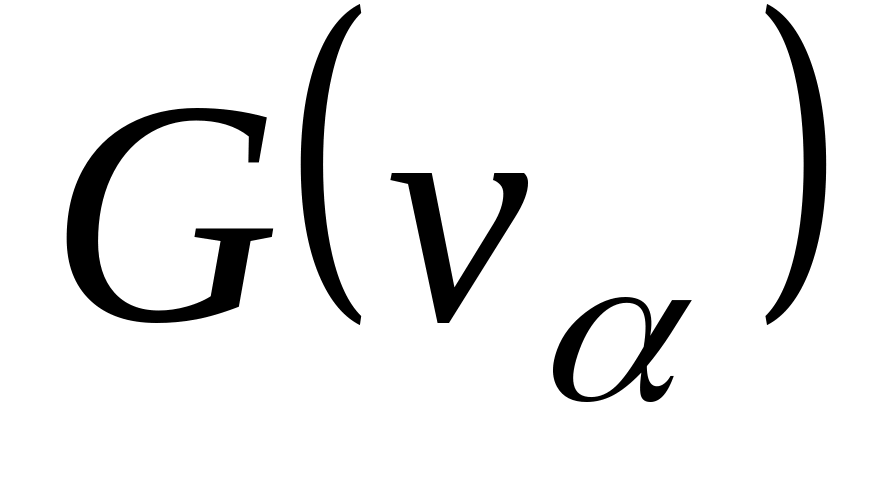вершины графа, сопоставленного рассматриваемому корню.

4. Считаем конец построенного яруса корнем нового дерева.

5. Устанавливаем, взвешена ли вершина символом Ø . Если “нет”, то переходим к п.2, если “да” – то к п.6.

6. Каждая ветвь построенного дерева однозначно определяет полный подграф заданного графа G .

Закон поглощения. Если в k – ом ярусе дерева вершины vi и vj смежны, поддерево с корнем vi построено и если в поддереве с корнем vj появляется вершина vi , то соответствующая ветвь не строится.

Пример. Определить плотность графа G (рис. 5.10).

□ Используя алгоритм выделения полных подграфов, построим искомое дерево (рис. 5.11).

Здесь Ki – полные подграфы. Видно, что мощность носителей всех подграфов равна трем, значит

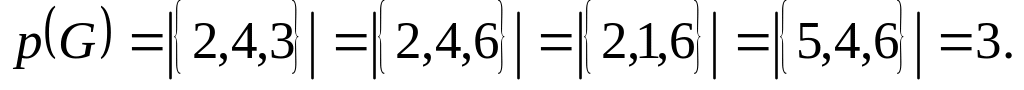
Каждое множество состоит из попарно смежных вершин. ■

§ 6. Раскраска графа

К построению раскрасок графов сводится целый ряд практических задач, например, задачи составления расписаний, распределения оборудования, проектирования некоторых технических изделий.

Раскраской вершин графа называется разбиение носителя V графа G на подмножества, при котором каждое подмножество Vi не содержит ни одной пары смежных вершин.

Каждому подмножеству сопоставляется цвет, в который окрашивают элементы этого подмножества.

Хроматическим числом 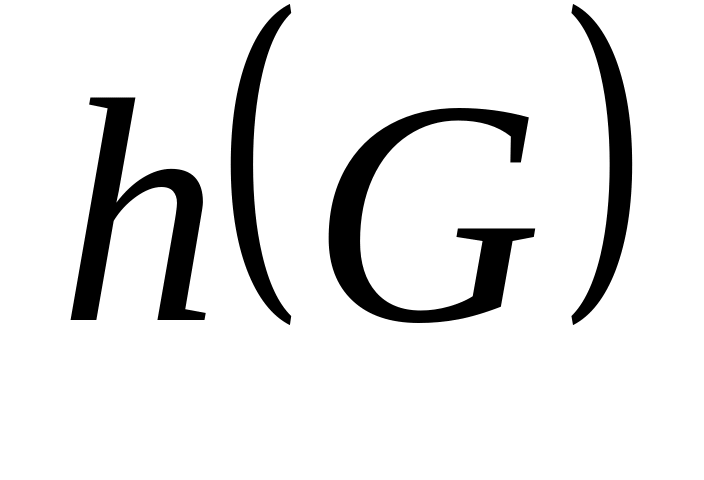графа G называется минимальное число п (число красок), для которого граф имеет п – раскраску.

Если = п , то граф называется п – хроматическим .

Если 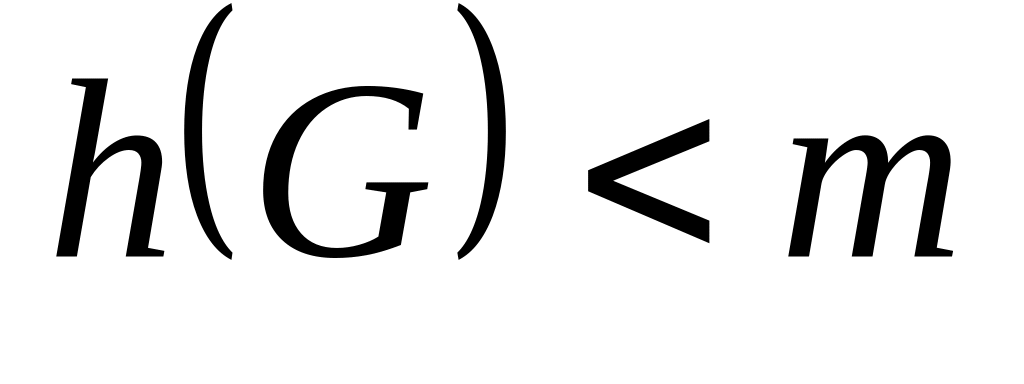(т – число красок и раскраска удовлетворяет определению), то граф называется т – раскрашиваемым .

1 – хроматический граф – это пустой граф.

Теорема 1. Граф является 2 – хроматическим тогда и только тогда, когда он не содержит циклов нечетной длины.

Источник

Раздел 1. Математическая логика

Тема 1. Логика высказываний

Тема 2. Булевы функции

Тема 3. Логика предикатов

Тема 4. Метод резолюций

Раздел 2. Теория графов

Тема 5. Раскраски

При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин. Довольно часто дополнительно требуется, чтобы таких классов было наименьшее число. В теории графов подобные задачи формулируются в терминах раскраски вершин графа.

В теме рассматриваются только обыкновенные графы.

§1. Хроматическое число

§2. Оценки хроматического числа

Если нет формулы, позволяющей (точно) вычислить хроматическое число, то можно попытаться найти приемлемые оценки для этого числа.

Рассмотрим вначале нижние оценки для c (G).

Начнем с оценки, связанной с плотностью графа.

Определение. Плотностью j (G) графа G называется наибольшее число вершин полного подграфа графа G.

Следующее утверждение очевидно.

Предложение 1. Для любого графа G выполняется неравенство

Для графов, изображенных на рис. 5.4, это неравенство превращается в равенство. Однако, как показывает следующее утверждение разность между c (G) и j (G) может быть сколь угодно большой.

Теорема 5.2. Для всякого k ≥ 2 существует граф G такой, что j (G)=2 и c (G)=k.

Доказательство. Для связного не одноэлементного графа G равенство j (G)=2 означает, что G не содержит треугольников, т.е. трехэлементных полных графов. Индуктивно построим последовательность G2,G3,…,Gk,… графов без треугольников, для которых c (Gk)=k.

Положим G2=K2. Предположим, что граф Gk=(Vk,Ek) уже построен и Vk=1,v2,…,vn>. Пусть Vk′=1′,v2′,…,vn′>, Vk Ç Vk′= Æ и v Ï Vk È Vk′. Множество вершин графа Gk+1 будет равно Vk È Vk′ È .Множество ребер этого графа получается добавлением к Ek ребер, соединяющих вершину vi′ c вершинами из Vk, которым смежна vi в графе Gk, и ребер, соединяющих v со всеми вершинами из Vk′. Переход от G2 к G3 показан на рис. 5.5, а переход от G3 к G4 – на рис. 5.6.

Докажем, что Gk+1 не содержит треугольников. Действительно, треугольник не может содержать вершину v, поскольку она смежна только вершинам V’, которые попарно не смежны. По той же причине треугольник не может содержать две вершины из V′. Если же в графе Gk+1 попарно смежны вершины vi′, vp, vq, то в Gk попарно смежны вершины vi, vp, vq. Поскольку по предположению индукции в Gk нет треугольников, то и в Gk+1 нет треугольников.

Проверим, что c (Gk+1)=k+1. Пусть

правильная раскраска графа G. Продолжим функцию f на Vk′ È следующим образом: f(vi′)=f(vi), f(v)=k+1. Мы получим правильную раскраску графа Gk+1 (k+1) краской. Следовательно, c (Gk+1) ≤ k+1. Предположим, что Gk+1 можно правильно раскрасить k красками. Тогда вершины из Vk′ раскрашены не более, чем k-1 краской, поскольку одна краска израсходована на вершину v. Если перекрасить вершины из Vk следующим образом: вершину vi покрасить той же краской, что и vi′, то мы получим правильную раскраску графа Gk не более, чем k-1 красками. Полученное противоречие доказывает, что граф Gk+1 нельзя правильно раскрасить k красками. Таким образом, X(Gk+1)=k+1.

Вторая оценка использует число независимости графа.

Определение. Множество попарно несмежных вершин графа называется независимым множеством. Числом независимости b (G) графа G называется наибольшее число вершин независимого множества.

Так для графов G1 и G2, изображенных на рис.5.1, получаем, что b (G1)=3, b (G2)=2.

Предложение 2. Для любого графа G выполняется неравенство

Доказательство. Пусть c (G)=k. Тогда при оптимальной раскраске графа G множество V разбивается на k классов V1,V2,…,Vk одинаково раскрашенных вершин. Каждое из множеств Vi является независимым и поэтому ½ Vi ½ £ b (G). Тогда

Разность c (G) — n/ b (G) тоже может быть сколь угодно большой, как и в первом случае. Только установить это можно гораздо проще. Пусть Н – полный граф с множеством вершин V=1,v2,…,vk>. Добавим к V еще k новых вершин v1′,v2′,…,vk′ и k новых ребер, соединяющих вершины vi′ и vi для 1 £ i £ k. Полученный граф обозначим буквой G. Легко видеть, что c (G)=k, a n/ b (G)=2.

Нижние оценки хроматического числа в предложениях 1 и 2 обладают еще одним недостатком: задача вычисления чисел j (G) и b (G) столь же сложна, как и задача вычисления хроматического числа. (Это утверждение здесь мы пояснять не будем, подробно о сложности задач см. в книге Гэри и Джонсона .)

Известны нижние оценки хроматического числа, использующие «легко вычисляемые» величины. Укажем одну из них.

Предложение 3. Для любого графа G выполняется неравенство

Отметим, что для полного графа 2m=n(n-1), поэтому для произвольного графа n 2 –2m > 0. (По поводу доказательства предложения 3 см. книгу Н. Кристофидеса, стр.78.)

Из верхних оценок укажем одну, приведенную в теореме 5.3, которую часто называют теоремой Брукса. (Теорема доказана Бруксом в 1941г.) Через D (G) обозначим наибольшую степень вершин графа G.

Теорема 5.3. Пусть G=(V,E) – связный неполный граф и D (G) ³ 3. Тогда c (G) £ D (G).

Доказательство. В силу теоремы можно считать, что G – двусвязный граф.

Докажем вначале, что в G существуют (различные) вершины u и v такие, что d(u,v)=2 и граф G–u–v является связным. Обозначим через D множество доминирующих вершин графа, т.е. таких вершин, что любая другая вершина смежна с этой вершиной. Если вершинная связность k (G) больше или равна трех или D ¹ Æ , то существование указанных вершин u и v достаточно очевидно. Действительно, поскольку G неполный граф, то в нем найдутся вершины u и v такие, что d(u,v)=2. Если k (G) ³ 3, то их удаление не нарушит связности графа. (Напомним, что k (G) – наименьшее количество вершин, удаление которых нарушает связность.) Эти вершины не принадлежат D, поэтому если D ¹ Æ , то в графе G–u–v найдется доминирующая (в нем) вершина. Отсюда следует, что граф G–u–v является связным и d(u,v)=2.

Будем считать, что k (G) 3 и D= Æ . Поскольку G не содержит точек сочленения, то из неравенства k (G) 3 следует равенство k (G)=2. Возьмем вершину х для которой r (x) ³ 3. Такая вершина существует, поскольку D (G) ³ 3.

Рассмотрим граф G’=G – x. Так как k (G)=2, то G’ – связный граф. Если k (G’)=2, то в качестве u возьмем х, а в качестве v – вершину графа G, находящуюся от х на расстоянии 2. (Такая вершина v существует, поскольку D= Æ .)

Предположим теперь, что k (G’)=1, т.е. что граф G’ содержит (хотя бы одну) точку сочленения. Пусть В – концевой блок графа G’ и а – точка сочленения графа G, принадлежащая этому блоку. Тогда вершина х смежна хотя бы с одной вершиной блока В, отличной от а. Поскольку в противном случае точка а будет точкой сочленения графа G (см. рис. 5.7, где прямоугольниками изображены блоки графа G – х).

Возьмем два концевых блока В и С графа G – х и в блоках В и С точки u и v, смежные с х. Поскольку u и v не смежны, то d(u,v)=2. Легко видеть, что граф G – u – v связен. Действительно, графы B – u и C – v являются связными, а поэтому граф G – u – v – x является связным. Но r (х) ³ 3 и поэтому граф G – u – v также связный.

Итак, в G существуют вершины u,v такие, что d(u,v)=2, вершины u и v смежны с вершиной х и граф G – u – v является связным. Упорядочим вершины графа G – u – v следующим образом. На первое место поставим вершину х1, на второе – одну из смежных с х вершин (напомним, что в графе G r (х) ³ 3). Предположим, что мы упорядочили i вершин графа G – u – v и получили последовательность: x1,x2,…,xi. Среди оставшихся вершин графа G – u – v найдется вершина w, которая смежна одной из вершин x1,…,xi, поскольку G – u – v связный граф. Положим xi+1=w. В результате мы получим последовательность x1,…,xn-2 графа G – u – v такую, что каждая вершина xi (1 £ i £ n-2) смежна хотя бы одной вершине с меньшим номером.

Для удобства обозначим D (G) буквой k и раскрасим граф G k красками следующим образом. Вершины u и v покрасим первой краской. Вершины графа G – u – v расположены в указанную выше последовательность x1,x2,…,xn-2. Эти вершины раскрашиваем, начиная с xn-2. Вершину xn-2 раскрасим первой краской, если она не смежна u и v, и второй, если xn-2 смежна одной из этих вершин. Предположим, что вершина xi (2 i £ n-2) уже раскрашена. Тогда, поскольку r (xi-1) £ k и xi-1 смежна хотя бы одной вершине с меньшим номером, то для раскраски вершин, смежных с xi-1, израсходовано менее k красок. Следовательно, осталась краска для xi-1. Итак, все вершины графа G, кроме х1, раскрашены. Так как х1 смежна вершинам u и v, раскрашенным одной краской и r (х1) £ k, то для раскраски вершин, смежных х1, израсходовано менее k красок. Это означает, что осталась краска для х1. В итоге мы получаем правильную раскраску графа G.

Верхняя оценка хроматического числа, даваемая теоремой Брукса, является удовлетворительной для тех графов, степени вершин которых примерно одинаковы. В общем же случае разность между D (G) и c (G) может быть сколь угодно большей. Рассмотрим граф, изображенный на рис. 5.8. Очевидно, что c (G)=2 и в то же время, D (G)=l.

Итак, общий итог «изысканий», проведенных в первом и втором параграфах, можно назвать неутешительным. Как мы видели, не существует формулы, позволяющей вычислить хроматическое число по «знакомым» величинам: число вершин, ребер, компонент связности, степени вершин, и нет достаточно хороших оценок для хроматического числа. Эта ситуация является отражением того факта, что задача вычисления хроматического числа является трудно решаемой, так же, как и задача нахождения гамильтонова цикла. Обсуждение алгоритмов вычисления хроматического числа выходит за рамки данного пособия, и мы ограничимся лишь тем, что приведем простой алгоритм нахождения правильной раскраски, близкой к оптимальной.

Алгоритм состоит в следующем. Упорядочиваем вершины графа G: V=1,v2,…,vn>.Вершину v1 красим первой краской. Предположим, что вершины v1,…,vi уже раскрашены и на это использовано l красок. Если на раскрашенные вершины, смежные с vi+1, использованы все краски, то vi+1 раскрашиваем l+1 краской. Если среди l красок найдется краска, которая не использована для вершин, смежных с vi+1, то вершину vi+1 красим этой краской.

Приведенный алгоритм часто называют алгоритмом последовательной раскраски. Нетрудно привести примеры, когда такая раскраска не является оптимальной.

Источник

Источник

Сетевой анализ. Работа с Gephi. {#сетевой-анализ-работа-с-gephi}

Что такое граф? {#что-такое-граф}

Граф, или сеть– это модель, состоящая изузлови связей между ними, илиребер. По-английски это называется_nodes (vertices)и_edges.

Узлы в графах могут группироваться в сообщества.Сообщество– это плотный подграф, где все (или почти все) узлы связаны между собой. Графы бывают:

  • ориентированные и неориентированные (связи-стрелочки vs обычные связи)
  • связные и несвязные (все узлы связаны vs есть узлы, которые оторваны от основного графа).
  • взвешенные и невзвешенные (связи имеют некоторое числовое значение или нет)

В лекции вы видели много разнообразных примеров графов, вот еще один. Здесь станции – это узлы, а перегоны – ребра. Когда вы рассчитываете расстояние в пути, вы работаете со взвешенным графом: каждый перегон оценивается в несколько минут.

А вот так выглядит интернет!

А вот так выглядит алгоритм машинного обучения

Метрики {#метрики}

Метрика– это результат измерений, проведенных определенным способом. Представьте, что вы выбираете материал для реферата на тему “Слово о полку Игореве”: у вас есть оригинальный текст в 50 страниц, современная книга А.А. Зализняка “Слово о полку Игореве: взгляд лингвиста” в 500 страниц и англоязычная статья “The Igor Tales and Their Folkloric Background” в 100 страниц. Если метрикой для вас является количество страниц, то вы выберете оригинальный текст, а если простота чтения – то современную русскоязычную книжку.

Степень, или мощность узла(degree)– это количество его связей.

Взвешенная степень(weighed degree)– это количество связей узла, разделенное на общее количество связей в графе.

Важность узла можно определять разными способами:

  • degree centrality
    : у кого больше связей, тот и важнее
  • closeness centrality
    : чем центральнее узел (т.е. чем короче путь от него до всех остальных узлов), тем он важнее
  • betweenness centrality
    : количество кратчайших путей, проходящих через узел
  • eigencentrality
    : чем больше друзей у твоих друзей, тем ты важнее

Коэффициент ассортативности_(assortativity coefficient)_определяет, с кем связаны “важные” узлы: если с другими “важными” узлами, то значение коэффициента высокое, а если нет – низкое.

Коэффициент кластеризации_(clustering coefficient) –_степень взаимодействия между собой ближайших соседей узла, т.е. вероятность того, что ближайшие соседи узла будут связаны не только с ним, но и между собой.

Плотность графа_(density) –_отношение числа ребер к максимально возможному. В сообществах высокий коэффициент кластеризации и высокая плотность.

Модулярность_(modularity)_показывает, насколько при заданном разбиении графа на группы плотность связей внутри группы больше плотности связей между группами. С помощью этой метрики граф разбивается на сообщества.

Форматы графов {#форматы-графов}

Граф записывается в виде текстового (.gml) или XML-файла (.graphml, .gexf), где перечисляются все узлы, ребра и их атрибуты – например, название узла или вес ребра. Вот так выглядят файлы .gml и .gexf соответственно.

Gephi {#gephi}

Gephi– программа для визуализации графов. Скачать ее можноотсюда, авот здесьинструкция по работе с ней.

С помощью Gephi можно делать очень красивые и наглядные картинки. Вот пример из работы польского специалиста по стилометрии Яна Рыбицки – хронология романов Ч. Диккенса, построенная по наиболее частотным словам в тексте.

А это граф русских романов XIX века от команды тьюториала по стилометрии на II московско-тартусской школе по Digital Humanities.

Графы, созданные в Gephi, можно не только сохранять как картинки или pdf, но и публиковать в интернете (например, на GitHub) с помощью плагина Sigma. Вотпример интерактивного графапо Оссиановским поэмам Макферсона.

А теперь давайте разберемся, как всё это это сделать.

Работа с графом в Gephi {#работа-с-графом-в-gephi}

Мы будем работать с контактами внутри сообщества дельфинов-афалин.Здесьможно скачать данные (в gephi можно загружать файлы не только в формате .gml, .graphml, .gexf, но и в табличных форматах (.csv, .tsv,).Здесьесть подробный разбор этого. При запуске программы появляется приветственное окошко.

Нажимаем_Создать новый проект_, затем_Файл_→_Import Spreadsheet_. Выбираем файл out.dolphins.tsv →_Open_(Параметры: Separator:Tab Import As:Edges Table, остальные не меняем).

Если вы импортируете файл с графом, то после импорта Gephi покажет отчет с характеристиками графа, а также количеством узлов и ребер.

Сразу после загрузки граф будет выглядеть вот так.

Gephi позволяет вручную менять размер, цвет и подписи узлов и рёбер. Для этого нужно использовать панель инструментов слева от графа. Кроме того, узлы можно перетаскивать мышкой.

Чтобы сделать его более наглядным, можно настроить свет и размер узлов и ребер в соответствии с их атрибутами.

Начнём с того, что изменим размер узлов в зависимости от их степени, для этого в разделе Appearance нажмём_Nodes_и значок размера.

После чего выберем_Ranking_→ Degree. Затем_Применить_. Чем больше разброс между минимальным и максимальным значением, тем наглядней получается граф. Может получится, например, так:

Следующим шагом посчитаем модулярность, чтобы разбить наш граф на сообщества. Это делается во вкладке «Статистика» на рабочей панели справа.

Теперь перейдем к изменению цвета узлов и ребер. Это делается с помощью значка палитры во вкладке «Appearance» на левой рабочей панели. По умолчанию все узлы и ребра раскрашены одним цветом (Unique), но мы раскрасим их в соответствии с тем, к каким сообществам они принадлежат (Partition → Modularity Class).

В правом нижнем углу вы увидите маленькую надпись Palette – нажав на нее, можно выбрать цвета, в которые будут раскрашены узлы. В палитрах по умолчанию всего 8 цветов, для больших графов нужно больше. Для таких случаев в Gephi предусмотрена возможность сгенерировать палитру: чтобы цветов было столько, сколько разных значений у выбранного атрибута, нужно просто снять галочку с «Limit number of colours», а затем нажать Generate и OK. Можно также выбрать стиль палитры (параметр Presets): пастельные тона, темные цвета, насыщенные цвета и т.п.

После этих манипуляций получится примерно такая картина. Управлять масштабом графа можно с помощью колеса мыши, а кнопка с лупой в нижней части панели инструментов слева от рабочей области центрирует граф.

По умолчанию граф уложен случайным образом – то есть то, где располагается узел и какие узлы находятся рядом с ним, ничего не значит. Попробуем сделать картинку более осмысленной с помощью какого-нибудь алгоритма укладки. Меню «Укладка» находится в левом нижнем углу. Вот, например, алгоритм Fruchterman Reingold, который укладывает узлы по кругу (обратите внимание, как узлы одного цвета, принадлежащие к одному сообществу, притянулись друг к другу).

Кстати, необязательно ждать, пока укладка закончится (спойлер:она может идти вечно) — если результат вас устраивает, можно просто нажать_Стоп_. Если вам кажется, что узлы расположены слишком тесно, можно использовать «Расширение» (Expand). Если вам кажется, что граф вверх ногами, то можно использовать «Поворот» (Rotate)

Выберите самую репрезентативную, на ваш взгляд, укладку. Может получиться так:

Кроме того, вы можете захотеть добавить подписи узлов (они называютсяметками, или_labels_). Для работы с ними предусмотрена панель инструментов снизу от области с графом. Чтобы подписи появились, нужно нажать на черную букву Т; правее можно выбрать цвет, шрифт и кегль (в этом датасете подписей нет, но вообще это может пригодиться).

**NB!**В Gephi нет кнопки “Назад”, так что будьте осторожны с изменениями, чтобы потом не пришлось все переделывать с самого начала.

Далее приводится другой пример графа: естественно, такие же манипуляции можно проводить и с любым другим.

После включения меток вы скорее всего столкнетесь с тем, что они наползают друг на друга. Чтобы этого избежать, нужно запустить алгоритм “Укладка меток”. Картинки ниже – до и после укладки.

Все это время мы находились во вкладке “Обработка”. Следующая вкладка, “Лаборатория данных”, позволяет нам посмотреть на данные в табличном виде, добавить или удалить столбцы и строки, отредактировать или отфильтровать их с помощью регулярных выражений и экспортировать данные в csv (или, наоборот, импортировать их из него, что очень удобно).

Наконец, в последней вкладке, “Просмотр”, можно увидеть красиво отрисованный граф, а не рабочую версию. Единственное что – отображение меток придется включить заново, но уже в этой вкладке на панели инструментов слева. Если у вас большой граф, то лучше снять галочку с параметра “Пропорциональный размер” и немного увеличить шрифт. Остальные параметры подписей можно настроить по своему вкусу.

Скорее всего, сначала вы увидите просто белое поле без графа – чтобы он отрисовался, нужно нажать кнопку “Обновить” внизу. То же самое нужно делать после любых изменений, если вы хотите их увидеть. Мой граф в итоге выглядит вот так.

Он достаточно хорошо интерпретируется:

  • темно-зеленые узлы – это однокурсники из Вышки
  • светло-зеленые узлы – это однокурсники из МГУ
  • розовые узлы – это разные лингвисты (преподаватели Вышки, студенты Вышки не с моего курса, студенты ОТиПЛа МГУ)
  • бирюзовые узлы – это друзья из МГУ курсом старше
  • голубые узлы – это разные кельтологи и скандинависты
  • бордовые узлы – это однокурсники из СПбГУ
  • оранжевые узлы – это люди из родного города
  • темно-фиолетовые узлы – это коллеги по работе
  • светло-сиреневые узлы – это коллеги по походам
  • желтые узлы – московские друзья

Экспорт графа {#экспорт-графа}

Граф можно сохранить в png или в pdf: если вам нужен небольшой файл и не важна детальность, то лучше выбрать png, а если вы хотите рассматривать граф при каком угодно приближении без потери качества, то лучше выбрать pdf. Экспортировать граф можно двумя способами: с помощью соответствующей кнопки в левом нижнем углу в “Просмотре” или в меню “Файл > Экспорт”.

Кроме того, можно экспортировать не статичную картинку, а динамический граф и выложить его в интернет – как исследование поэм Макферсона, помните? Для этого нужно установить плагинSigma Exporterв меню “Сервис > Подключаемые модули > Доступные подключаемые модули” и перезагрузить Gephi. Не забудьте сохранить ваш проект (“Файл > Сохранить проект”, или Ctrl + S) перед перезагрузкой, чтобы не потерять работу!

После этого можно сохранять граф в Sigma (“Файл > Экспорт > Sigma.js template”).

В появившемся окне нужно указать путь к папке, куда вы хотите экспортировать проект, и данные для легенды: название и кратое описание графа, а также то, что обозначают узлы, ребра и их цвета.

После этого в указанной директории появится папка network. Все файлы из этой папки нужно загрузить в новый репозиторий на гитхабе. Если вы забыли что-то указать при экспорте, это можно будет поправить в файле config.json вручную, открыв его в блокноте. Вот список файлов, который должен оказаться в вашем репозитории.

Теперь, когда все нужные файлы лежат в репозитории, отправляемся в его настройки и прокручиваем их вниз до пункта GitHub Pages, а затем в Source выбираем Master branch и нажимаем кнопку Save. У вас должно появиться зеленое уведомление с адресом вашей странички формата

https://username.github.io/repository_name

Получиться должно что-то вот такое. Если хотите, можете поэкспериментировать с файлом index.html, чтобы избавиться от элементов, которые вам не нравятся (например, от пустого поля в верхней части легенды).

Обратите внимание, что все селекторы должны работать!

Полезная ссылка {#полезная-ссылка}

Туториал

Датасеты {#датасеты}

https://github.com/gephi/gephi/wiki/Datasets

http://www-personal.umich.edu/~mejn/netdata/

http://konect.uni-koblenz.de/

Источник

Добавить комментарий