Расчет теоретической плотности кристаллических веществ
Теоретическую
плотность кристаллических веществ
нередко и наиболее точно определяют с
помощью рентгенографического метода
(рассчитанная таким образом плотность
носит название рентгенографической).
При определении плотности по данным
рентгенографического анализа используется
связь значений плотности вещества с
атомными массами составляющих его
элементов и объемом, занимаемым ими.
Для
определения рентгенографической
плотности необходимо знать объем
элементарной ячейки (V0),
число атомов (Z)
в ней и суммарную массу этих атомов.
Тогда масса атомов в элементарной ячейке
равна
(A/N0)
Z,
[г], где
A/N0
– масса одного атома в граммах; N0
= 6,0224102 (число Авогадро),
А – грамм–атом.
Таким образом,
плотность равна:
ρ
= (A·Z
/ N0)·(1/
V0),
[г/см3],
При
переводе значений объема элементарной
ячейки из кубических ангстремов в
кубические сантиметры в знаменателе
формулы появляется V0·10–24,
тогда
ρ=1,6602
(A·Z/V0),
[г/см3].
Объем
элементарной ячейки определяется исходя
из сингонии и формально–геометрических
соображений (Приложение 3).
Значение
рассчитанной таким образом плотности
кристаллического вещества характеризует
идеализированную кристаллическую
решетку с реальными параметрами.
Справочные значения плотности, как
правило, будут отличаться от
рентгенографической в меньшую или
большую сторону. Эта разница может быть
вызвана наличием в реальных кристаллах
примесей, дефектов кристаллической
решетки, внутренних напряжений
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Дайте
определение кристаллического тела. -
Что
понимают под атомно–кристаллической
структурой? -
Что
такое кристаллическая решетка? -
Назовите
основные типы кристаллических решеток
для металлов. -
Сколько
атомов приходится на элементарную
ячейку ОЦК, ГЦК и ГПУ решеток? -
В
каких единицах измеряется период
решетки? -
Что
понимают под индексом Миллера? -
Что
характеризует координационное число? -
Дайте
понятие плотности поликристаллических
веществ.
ПОРЯДОК ВЫПОЛНЕНИЯ
РАБОТЫ
1.
Изучить предложенную теоретическую
часть и дидактическое обеспечение.
2. Выбрать вариант в соответствии с
порядковым номером в учебном журнале
и выполнить следующие задания:
Задание
1. Из таблицы 1 взять предложенные
исходные данные в соответствии с номером
выбранного варианта.
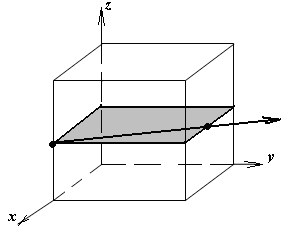
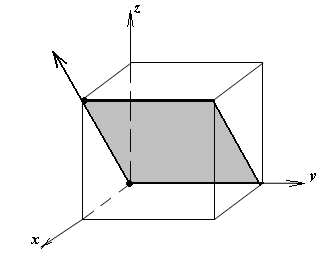
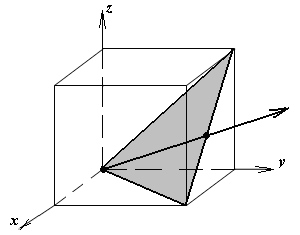
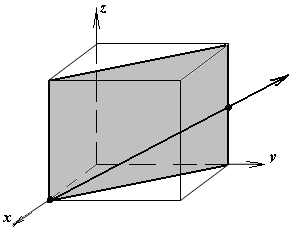
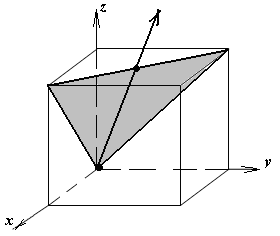
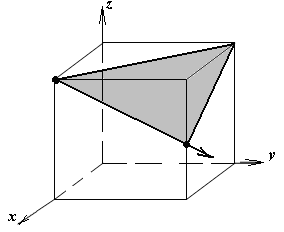
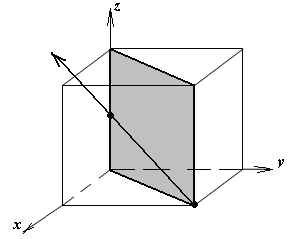
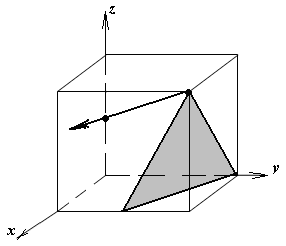
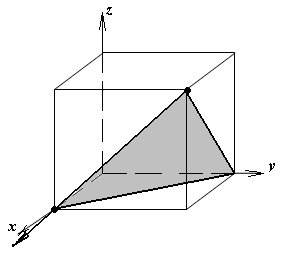
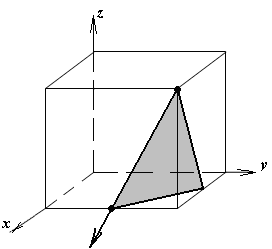
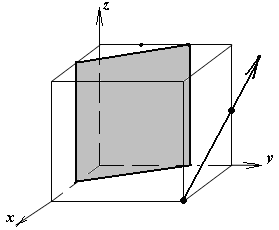
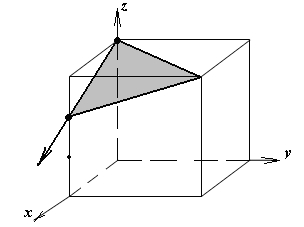
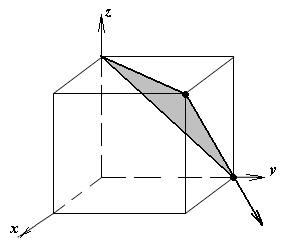
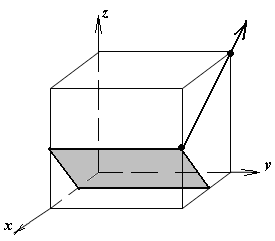
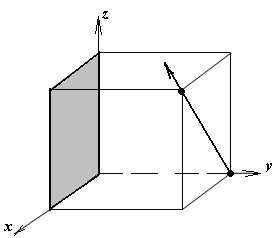
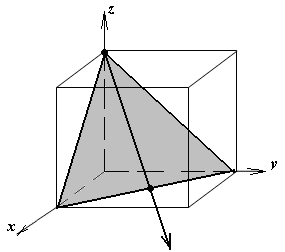
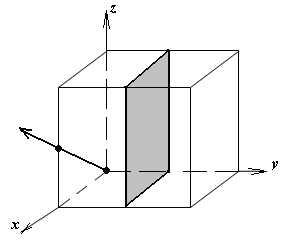
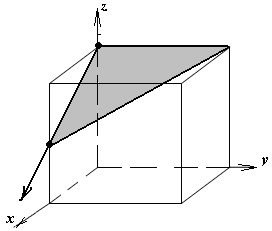
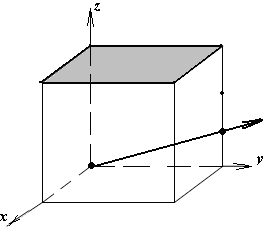
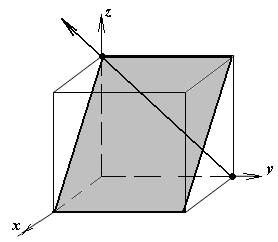
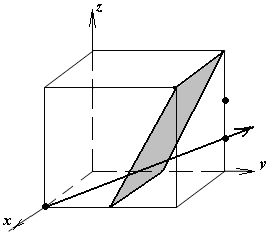
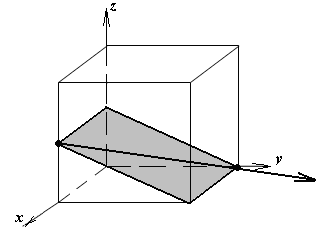
1.а
определить индексы плоскости и
направления, изображенных на рисунке;
1.б изобразить в элементарной ячейке
кубической решетки плоскость и
направление, индексы которых даны в
задании.
Задание 2. Рассчитать плотность
металла, используя данные о его
кристаллической решетке в соответствии
с номером варианта (таблица 2).
Формулы для расчета объема элементарной
ячейки приведены в приложении 2.
Сравнить полученные результаты расчета
со справочными данными (Таблица 3).
3. Сделать вывод по результатам работы.
4. Оформить отчет.
СОДЕРЖАНИЕ ОТЧЕТА
-
Тема
работы, номер варианта. -
Рисунок
элементарной ячейки кубической решетки,
приведенный в задании с указанием
найденных индексов Миллера; рисунок
элементарной ячейки с изображением
плоскости и направления, приведенных
в задании. -
Расчет
плотности металла. -
Вывод
по работе.
Таблица 1
Варианты
задания 1
|
№ варианта |
Задание Определить |
Задание Изобразить |
|
1 |
2 |
3 |
|
1 |
|
( [ |
|
2 |
|
[ |
|
3 |
|
( [ |
|
Продолжение |
||
|
1 |
2 |
3 |
|
4 |
|
(1 [1 |
|
5 |
|
( [ |
|
6 |
|
( [ |
|
Продолжение |
||
|
1 |
2 |
3 |
|
7 |
|
( [ |
|
8 |
|
( [ |
|
9 |
|
( [ |
|
10 |
|
( [ |
|
Продолжение |
||
|
1 |
2 |
3 |
|
11 |
|
( [ |
|
12 |
|
( [ |
|
13 |
|
( [ |
|
Продолжение |
||
|
1 |
2 |
3 |
|
14 |
|
( [ |
|
15 |
|
( [ |
|
16 |
|
( [ |
|
17 |
|
( [ |
|
Продолжение |
||
|
1 |
2 |
3 |
|
18 |
|
( [ |
|
19 |
|
( [ |
|
20 |
|
( [ |
|
Продолжение |
||
|
1 |
2 |
3 |
|
21 |
|
( [ |
|
22 |
|
( [ |
|
23 |
|
( [ |
|
Окончание таблицы |
||
|
1 |
2 |
3 |
|
24 |
|
( [ |
|
25 |
|
( [ |
Таблица 2
Варианты задания 2
|
№ ва-риа-нта |
Наименование |
Синго-ния |
Кристал-лическая |
Парамет-ры |
Основные |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
Золото |
Куби-ческая |
ГЦК |
а=4,0783 |
Основной |
|
2 |
Медь |
Куби-ческая |
ГЦК |
а=3,6153 |
Ковкий, . |
|
3 |
Платина |
Куби-ческая |
ГЦК |
а=3,924 |
Температура |
|
4 |
Серебро |
Куби-ческая |
ГЦК |
а=4,0856 |
Применяется |
|
5 |
Алюминий |
Куби-ческая |
ГЦК |
а=4,041 |
Температура |
|
6 |
Железо |
Куби-ческая |
ОЦК |
а=2,860 |
Твердость |
|
Продолжение |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
Никель |
Куби-ческая |
ОЦК |
а=3,489 |
Электропроводен, |
|
8 |
Магний |
Гекса-гональ-ная |
ГПУ |
а=3,103 с=5,200 |
Температура |
|
9 |
Литий |
Куби-ческая |
ОЦК |
а=3,509 |
Относится |
|
10 |
Бериллий |
Гекса-гональ-ная |
ГПУ |
а=2,286 с=3,584 |
Легкий, |
|
11 |
Натрий |
Куби-ческая |
ОЦК |
а=4,291 |
Относится |
|
12 |
Калий |
Куби-ческая |
ОЦК |
а=5,247 |
Относится |
|
Продолжение |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
13 |
Кальций |
Куби-ческая |
ГЦК |
а=5,582 |
Относится |
|
14 |
Титан |
Гекса-гональ-ная |
ГПУ |
а=2,950 с=4,683 |
Легкий, |
|
15 |
Ванадий |
Куби-ческая |
ОЦК |
а=3,028 |
Твердый, |
|
16 |
Хром |
Куби-ческая |
ОЦК |
а=2,885 |
На |
|
17 |
Кобальт |
Гекса-гональ-ная |
ГПУ |
а=2,505 с=4,089 |
Ферромагнитен, |
|
18 |
Цинк |
Гекса-гональ-ная |
ГПУ |
а=2,665 с=4,947 |
Температура |
|
19 |
Цирконий |
Гекса-гональ-ная |
ГПУ |
а=3,231 с=5,731 |
Твердый, |
|
Окончание |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
20 |
Ниобий |
Куби-ческая |
ОЦК |
а=3,301 |
Тугоплавкий |
|
21 |
Молибден |
Куби-ческая |
ОЦК |
а=3,147 |
Тугоплавкий |
|
22 |
Кадмий |
Гекса-гональ-ная |
ГПУ |
а=2,979 с=5,618 |
Мягкий, |
|
23 |
Вольфрам |
Куби-ческая |
ОЦК |
а=3,165 |
Наиболее |
|
24 |
Свинец |
Куби-ческая |
ГЦК |
а=4,950 |
Тяжелый, |
|
25 |
Барий |
Куби-ческая |
ОЦК |
а=5,025 |
Мягкий. |
Таблица
3
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Полезное
Информационные и обучающие видеоролики, вопросы и ответы, техническая документация и наша книга
Глава 1 Некоторые современные представления о конституции и химической связи в кристаллах
1.2. Остовно-электронное моделирование конституции и химической связи в кристаллических соединениях
1.1. Структурная плотность кристаллических решеток твердых тел
Проблема структурной плотности кристаллических решеток как показателя условий минералообразования в свое время оживленно дискутировалась, соответствующий обзор приведен в работе (Евзикова и Ициксон, 1969), где авторами были предложены следующие параметры: η – число структурных единиц (атомов, молекул) в единице объема; Ω – абсолютная структурная рыхлость или объем, приходящийся в среднем на каждую структурную единицу минерала. Взаимосвязь этих параметров выражается формулой:
![]() (1.1)
(1.1)
где: η – число структурных единиц в формуле минерала; Z – число формульных единиц в элементарной ячейке, а Vo – ее объем.
При всей очевидной ясности физического смысла параметров η и Ω необходимо указать на их недостаточность для характеристики структурной плотности минералов. Это фактически признается самими авторами в статье (Евзикова и Ициксон, 1969), где для реальных, практических оценок используется другая характеристика структурной рыхлости:
![]() (1.2)
(1.2)
где: М – молекулярная масса минерала (г/моль); ρ – плотность минерала (г/см3); n – число атомов в формуле соединения.[1]
Вопреки первоначальной негативной оценке (Наковник, 1972; Доливо-Добровольский, 1973), мы считаем эту характеристику минералов весьма ценной, и ее возможности в описании и предсказании свойств минералов будут продемонстрированы в соответствующем разделе.
Представляется очевидным, что по своему физическому смыслу параметр h должен быть одинаковым для решеток различных минералов, обладающих одним и тем же структурным типом. Однако в реальности это далеко не соблюдается, в чем легко убедиться при сравнении параметров η для группы кристаллов, обладающих решеткой типа галита (NaCl) – галенита (PbS) (таблица 1.1).
Таблица 1.1
Параметры η для кристаллов с решеткой типа NаCl-PbS
| Кристалл | η | Кристалл | η | Кристалл | η |
| LiF | 0,122 | NaF | 0,081 | AgI | 0,036 |
| MgO | 0,107 | MnS | 0,056 | PbTe | 0,030 |
| FeO | 0,101 | NaCl | 0,045 | KI | 0,023 |
| MnO | 1,091 | PbS | 0,038 | RbI | 0,020 |
Крайние члены (первый и последний) в этой таблице различаются по параметру η более чем в 6 раз! Аналогичная картина имеет место при рассмотрении кристаллов других структурных типов. Следовательно, необходим другой, более корректный параметр структурной плотности, в качестве которого мы рекомендуем относительную структурную плотность кристаллической решетки – γ, который входит в новую кристаллохимическую формулу плотности минералов (Богданов и Зуев, 1991):
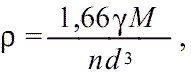 (1.3)
(1.3)
где 1,66 – константа, служащая для выражения плотности в г/см3, она равна атомной единице массы (а.е.м.) 1,66×10-24 г, поделенной на коэффициент перевода кубических ангстремов в кубические сантиметры (1 Å = 10-8 см); n – число атомов в формуле минерала; d (Å) – параметр межатомных расстояний.
В случае сложных минералов в качестве параметра d необходимо использовать усредненные для структуры величины межатомных расстояний. Например, для форстерита Mg2[6]Si[4]O4[4], в котором dср.(Mg-O6) = 2,12 Å и dср.(Si-O4) = 1,63 Å, усреднение межатомных расстояний с учетом координационных чисел (КЧ) атомов и их количеств в формуле минерала приводит к <d> = (2,12x6x2 + 1,63x4x1)/16 = 2,0 Å.
Параметры γ определяются КЧ атомов (см. рис. 1.1 и таблицу 1.2).
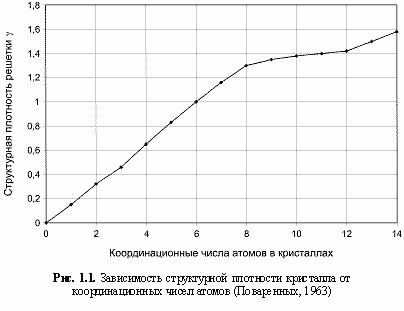
Таблица 1.2
Значения коэффициентов абсолютной и относительной плотности упаковки атомов в зависимости от их координационных чисел (Поваренных, 1963)
|
КЧ |
v, % | γ | КЧ | v, % | γ | КЧ | v, % | γ |
| 1 | 8,0 | 0,15 | 6 | 52,4* | 1,00 | 11 | 73,4 | 1,40 |
| 2 | 17,0 | 0,32 | 7 | 60,8 | 1,16 | 12 | 74,0* | 1,42 |
| 3 | 24,1(16,9*) | 0,46 | 8 | 68,0* | 1,30 | 13 | – | 1,50 |
| 4 | 34,0* | 0,65 | 9 | 70,0 | 1,35 | 14 | – | 1,58 |
| 5 | 43,5 | 0,83 | 10 | 72,3 | 1,38 |
Величины v, % характеризуют степень заполнения пространства равновеликими шарами (атомами). Параметры γ получены делением рассчитанных (отмечены звездочками) и интерполированных (рис. 1.1) величин v на величину v = 52,4%, отвечающую КЧ = 6 для структурного типа кристалла NaCl.
Однако можно вывести строгую формулу оценки g из кристаллохимических данных. Такую возможность дает сопоставление формулы (1.3) с известной рентгенометрической формулой плотности:
ρ= 1,66ZM / Vo (1.4)
Комбинируя эти две формулы, получим:
γ = Znd3 / Vo (1.5)
Расчет по формуле (1.5) для всех кристаллов (таблица 1.1) дает одинаковую структурную плотность γ = 1, что представляется вполне естественным, поскольку речь идет об одном и том же структурном типе кристаллов. Заметим, что формула (1.5) отличается от ранее предложенной формулы (1.1) лишь введением дополнительного параметра межатомных расстояний d, т. е. фактически уточняет последнюю.
В таблице 1.3 приведены вычисленные по формуле (1.5) параметры γ для некоторых других распространенных структурных типов минералов.
Таблица 1.3
Параметры структурной плотности для некоторых распространенных структурных типов минералов
| Структурный тип | γ | Структурный тип | γ |
|
NaCl, PbS |
1,0 |
Cu2O (куприт) |
0,49 |
|
CsCl, a-Fe |
1,3 |
SiO2 (кварц) |
0,33 |
|
Cu, Ag, Au |
1,42 |
CaF2 (флюорит) |
1,00 |
|
C (алмаз), ZnS |
0,65 |
CaWO4 (шеелит) |
0,85 |
|
FeS2 (пирит) |
0,87 |
Ca3Al2Si3O12 (гранат) |
0,88 |
|
FeS (троилит) |
1,00 |
Mg2SiO4 (форстерит) |
0,77 |
|
Al2O3 (корунд) |
0,82 |
ZrSiO4 (циркон) |
0,74 |
|
TiO2 (рутил) |
0,72 |
CaTiO3 (перовскит) |
1,31 |
|
PbCl2 (котунит) |
1,15 |
Ca5[PO4]3F (апатит) |
0,93 |
|
Al2SiO4F2 (топаз) |
0,62 |
CaCO3 (кальцит) |
0,65 |
|
Al2SiO5 (кианит) |
0,65 |
CaCO3 (арагонит) |
0,93 |
|
MgAl2O4 (шпинель) |
0,78 |
BaSO4 (барит) |
1,22 |
|
NaCaNb2O6F (пирохлор) |
0,95 |
K2SO4 (арканит) |
1,23 |
|
Fe2TiO5 (псевдобрукит) |
0,70 |
Ba[NO3]2 (нитробарит) |
0,87 |
|
YTiNbO6 (приорит) |
0,84 |
CePO4 (монацит) |
0,92 |
|
CaMn2O4 (марокит) |
1,01 |
FeWO4 (вольфрамит) |
0,75 |
|
La2O3 |
1,01 |
Cu2S (халькозин) |
0,81 |
|
CuO (тенорит) |
0,74 |
NiS (миллерит) |
0,93 |
|
CaSO4 (ангидрит) |
0,77 |
Na2SO4 (тенардит) |
0,82 |
|
Ni3S2 (хизлевудит) |
0,87 |
MgSiO3 (энстатит) |
0,68 |
|
Co4[As4]3 (скуттерудит) |
0,77 |
Mg7[Si8O22](OH)2 (антофиллит) |
0,62 |
|
S8 (самородная сера) |
0,34 |
Ca2Mg5[Si8O22](OH)2 (тремолит) |
0,72 |
|
Se (селен цепной стр-ры) |
0,46 |
Mg6[Si4O10](OH)8 (серпентин) |
0,62 |
|
В (кристаллический бор) |
0,76 |
Al2SiO5 (андалузит) |
0,56 |
|
MoS2 (молибденит) |
0,73 |
Al2SiO5 (силлиманит) |
0,55 |
|
Hg2Cl2 (каломелит) |
0,67 |
K2NiF4 |
1,1 |
|
BiF3 (Li3Bi) |
1,60 |
MgCu2 |
1,69 |
|
Mn2O3 (биксбиит) |
0,78 |
SnJ4 |
0,4 |
|
MoO3 (молибдит) |
0,67 |
PbO (глет) |
0,62 |
Согласно (Поваренных, 1963) (см. также таблицу 1.2), переход от γ к абсолютной плотности упаковки v осуществляется по формуле:
v = 52,4γ, (1.6)
где 52,4 есть выраженная в % степень заполнения пространства равновеликими соприкасающимися атомами-шарами в решетке типа NaCl с октаэдрической координацией атомов. Поскольку из формулы (1.6) γ = v / 52,4, то физический смысл параметра γ состоит в степени заполнения атомами пространства для рассматриваемого структурного типа по отношению к структурному типу NaCl. Соответственно параметр γ может быть охарактеризован как относительная структурная плотность решетки минерала.
Близким к параметру v, согласно данным работы (Наковник, 1972), является так называемый упаковочный индекс s (таблица 1.4).
Таблица 1.4
Сопоставление соответствующих параметров абсолютной плотности упаковки и упаковочных индексов в ряде минералов
| Минерал | v, % | s, % | Минерал | v, % | s, % | Минерал | v, % | s, % |
| Алмаз | 34 | 26 | Жадеит | 42 | 49 | Берндтит | 39 | 32 |
| Стишовит | 38 | 32 | Алтаит | 52 | 53 | Селлаит | 39 | 32 |
| Корунд | 43 | 45 | Пирит | 46 | 50 | Натролит | 27 | 33 |
| Мусковит | 43 | 42 | Кварц | 17 | 21 | Халькозин | 44 | 55 |
| Форстерит | 40 | 52 | Тридимит | 14 | 19 | Анальцим | 26 | 32 |
| Пироп | 47 | 46 | Андалузит | 30 | 31 | Торианит | 52 | 61 |
Рассмотренная концепция структурной плотности и способ нахождения параметра γ по формуле (1.5) относится, как отмечалось, к упаковкам равновеликих сфер. Однако эти данные можно распространять также и на катион-анионные упаковки разновеликих сфер, что следует из работы (Ye Danian, Zhang Jinmin, 1991). К тому же реальные, иначе называемые эффективными размеры катионных и анионных компонентов в гетероатомных минералах довольно близки, о чем свидетельствуют результаты соответствующих расчетов. Следует также оговориться, что формула (1.6) справедлива для упаковок из соприкасающихся сфер и следующих граничных условий 1,42 ≥ γ ≥ 0, где γ = 1,42 отвечает случаю плотнейших металлических упаковок с КЧ = 12.
Итак, структурную плотность кристаллов можно выражать либо в виде относительной (γ), либо в виде абсолютной (v) плотности упаковки атомов.
В качестве примеров в таблицах 1.5 и 1.6 приведены результаты оценок γ и v по формулам (1.5) и (1.6) для ряда групп полиморфных модификаций минералов. Поскольку в таблице 1.5 в пределах каждой из групп минералов (модификаций) идентичного состава КЧ атомов одинаковы, а межатомные расстояния М-Х довольно близки (Поваренных, 1966), то заметная разница в плотностях модификаций идентичного состава объясняется соответствующим различием плотностей упаковок (γ, v), причем эта зависимость, естественно, симбатная. В таблицах 1.6 и 1.7 имеет место более радикальный рост r в зависимости от роста γ(v), что связано с последовательным увеличением КЧ катионов в рассматриваемом ряду кристаллов состава MgSiO3 и SiO2.
Таблица 1.5
Структурная плотность некоторых кристаллических модификаций минералов в сопоставлении с их плотностью
| Формула | Название модификации | γ | v, % | ρ, г/см3 |
|
SiO2 |
Коэсит |
0,37 | 19,4 | 2,9 |
|
“ |
a-Кварц |
0,33 | 17,3 | 2,65 |
|
“ |
b-Кварц |
0,32 | 16,8 | 2,53 |
|
“ |
Кристобалит |
0,29 | 15,1 | 2,3 |
|
“ |
Тридимит |
0,275 | 14,4 | 2,2 |
|
“ |
Меланофлогит |
0,25 | 13,1 | 2,0 |
|
TiO2 |
Рутил |
0,72 | 37,7 | 4,3 |
|
“ |
Брукит |
0,70 | 36,7 | 4,1 |
|
“ |
Анатаз |
0,65 | 34,1 | 3,9 |
|
As2O3 |
Клодетит |
0,38 | 19,9 | 4,2 |
|
“ |
Арсенолит |
0,345 | 18,1 | 3,9 |
|
Sb2O3 |
Валентинит |
0,48 | 25,2 | 5,8 |
|
“ |
Сенармонтит |
0,46 | 24,1 | 5,6 |
|
FeS2 |
Пирит |
0,87 | 45,6 | 5,0 |
|
“ |
Марказит |
0,84 | 44,0 | 4,9 |
|
ZnS |
Сфалерит |
0,65 | 34,1 | 4,1 |
|
“ |
Вюртцит |
0,64 | 33,5 | 4,0 |
|
Cu2S |
Халькозин гекс. |
0,845 | 44,3 | 6,0 |
|
“ |
Халькозин ромб. |
0,81 | 42,4 | 5,8 |
|
FeS |
Троилит |
1,00 | 52,4 | 4,8 |
|
Fe0.88S |
Пирротин гекс. |
0,95 | 49,8 | 4,65 |
|
Fe0.82S |
Пирротин монокл. |
0,94 | 49,3 | 4,64 |
|
α-FeOOH |
Гетит |
0,76 | 39,8 | 4,3 |
|
γ-FeOOH |
Лепидокрокит |
0,72 | 37,7 | 4,1 |
|
Mg2SiO4 |
Тип K2NiF4 |
1,1 | 57,6 | 4,1 |
|
γ-Mg2SiO4 |
Рингвудит |
0,81 | 42,2 | 3,5 |
|
α-Mg2SiO4 |
Форстерит |
0,77 | 40,3 | 3,2 |
Таблица 1.6
Рост параметров структурной плотности и плотности в кристаллах в зависимости от увеличения КЧ катионов
| Кристаллическая фаза с указанием КЧкатионов и структурного типа | γ | v, % | ρ, г/см3 |
| Mg[6]Si[4]O3 (типа пироксена) | 0,68 | 35,6 | 3,2 |
| Mg[6]Si[6]O3 (типа ильменита) | 0,83 | 43,5 | 3,8 |
| Mg[7.5]Si[4.5]O3 (типа граната) | 0,88 | 46,1 | 3,7 |
| Mg[8]Si[6]O3 (типа перовскита) | 1,09 | 57,1 | 4,1 |
Таблица 1.7
Структурная, гравитационная и энергетическая плотности ряда модификаций SiO2 в сопоставлении с твердостью
| Модификации SiO2 | γ | ρ, г/см3 | Ev, кДж/см3 | НМ |
|
Кварц |
0,33 | 2,65 | 83 | 7 |
|
Коэсит |
0,37 | 2,93 | 91 | 7,5 |
|
Стишовит |
0,72 | 4,34 | 132 | 8,5 |
|
SiO2 типа пирита |
0,87 | 4,6 | 135 | 9,5 |
|
SiO2 типа флюорита |
1,00 | 4,8 | 139 | 10,9 |
|
SiO2 типа котунита |
1,15 | 5,1 | – | – |
Следует обратить внимание на то, что параметры γ не всегда дают корректные результаты в смысле предсказания стабильности структуры в зависимости от давления, определяемого глубиной образования. Так, по параметрам γ ряд глубинности соединений состава MgSiO3 (таблица 1.6) таков: пироксеновый тип → ильменитовый тип → гранатовый тип → перовскитовый тип, в то время как соответствующий экспериментальный ряд с указанием давлений переходов согласно данным работы (Ohtani, Kagawa, Fujino, 1991) отличается перестановкой мест ильменитового и гранатового типов фаз состава MgSiO3:
|
17 ГПа 22,5 ГПа 23 ГПа |
||||||
| Пироксеновый тип |
→ | Гранатовый тип |
→ | Ильменитовый тип |
→ | Перовскитовый тип |
Эти экспериментальные данные лучше интерпретируются с позиций использования параметров энергоплотности рассматриваемых кристаллических соединений состава MgSiO3 (Зуев, 1995).
Тем не менее, представляется вполне вероятным, что параметры структурной плотности кристаллических решеток минералов могут найти применение в качестве критериев глубинности минералообразования. Некоторые соответствующие данные по этому вопросу приведены в таблице 1.8, где типичные гипогенные (глубинные) и гипергенные (поверхностные) минералы весьма четко различаются по параметру γ: средняя величина γ для первых близка к 0,9, для вторых равна 0,45.
Таким образом, средние параметры γ типичных глубинных и поверхностных минералов различаются почти в два раза, а их соответствующие средние плотности (ρ) – в 1,3 раза. Это означает, что параметр γ более чувствителен, а потому и более информативен как критерий глубинности минералообразования по сравнению с параметром ρ. Как известно, типичная глубинная порода – кимберлит имеет в своем составе оливин, флогопит, пироп, циркон, диопсид (хром-диопсид), ильменит, перовскит и апатит. Все указанные минералы характеризуются довольно высокими параметрами γ (таблица 1.8).
Таблица 1.8
Сопоставление структурной и гравитационной плотностей для ряда глубинных и поверхностных минералов
| Гипогенныеминералы | γ | ρ, г/см3 | Гипергенныеминералы | γ | ρ, г/см3 |
|
Алмаз |
0,65 | 3,5 |
Лед |
0,24 | 0,92 |
|
Стишовит |
0,72 | 4,3 |
Опал |
0,25 | 2,2 |
|
Циркон |
0,74 | 4,7 |
Кварц |
0,33 | 2,65 |
|
Оливин |
0,77 | 3,6 |
Куприт |
0,49 | 6,1 |
|
Жадеит |
0,80 | 3,3 |
Сера |
0,34 | 2,1 |
|
Ильменит |
0,82 | 4,8 |
Арсенолит |
0,35 | 3,9 |
|
Диопсид |
0,83 | 3,3 |
Каолинит |
0,46 | 2,6 |
|
Флогопит |
0,84 | 3,0 |
Гиббсит |
0,53 | 2,4 |
|
Пироп |
0,89 | 3,55 |
Кальцит |
0,65 | 2,7 |
|
Апатит |
0,93 | 3,2 |
Гидрогетит |
<0,70 | 4,0 |
|
Троилит |
1,00 | 4,8 |
Гипс |
0,57 | 2,3 |
|
Периклаз |
1,00 | 3,6 |
Аурипигмент |
0,49 | 3,5 |
|
Перовскит |
1,31 | 4,0 |
Реальгар |
0,50 | 3,6 |
|
Рингвудит |
0,81 | 3,5 |
Азурит |
0,45 | 3,8 |
|
Средние параметры |
<0,87> | <3,8> |
Средние параметры |
<0,45> | <3,0> |
Интересно с позиций структурной плотности рассмотреть ряд глубинности минералов по И. В. Матяшу (Матяш, 1991), который связывает увеличение глубинности образования минералов с ростом их ионности (эффективных зарядов атомов кислорода) и плотности. Рост ионности, по И. В. Матяшу, приводит к образованию все более плотноупакованных, компактных структур. Значит, в этом случае вполне правомочно использование параметра структурной плотности γ соответствующих кристаллических решеток минералов.
Таблица 1.9
Ряд глубинности минералов (Матяш, 1991) в сопоставлении с параметрами: структурной плотности, ионности и удельной массовой энергии атомизации
| Минерал | γ | fi (Зуев, 1990) | Em, кДж/г | Минерал | γ | fi (Зуев, 1990) | Em, кДж/г |
|
Гидроксит (вода) |
0,25 | 0,33 | 53,9 |
Антофиллит |
0,62 | 0,60 | 29,8 |
|
Брусит |
0,68 | 0,57 | 34,3 |
Гиперстен |
0,68 | 0,60 | 29,0 |
|
Кварц |
0,33 | 0,5 | 31,3 |
Форстерит |
0,77 | 0,64 | 27,8 |
|
Серпентин |
0,60 | 0,54 | 31,8 |
Периклаз |
1,00 | 0,80 | 24,7 |
|
Тальк |
0,58 | 0,53 | 30,8 |
Как следует из таблицы 1.9, ряд глубинности минералов по И. В. Матяшу в целом подтверждается и дополнительно обосновывается использованием соответствующих параметров γ. Особое внимание заслуживает весьма тесная обратная корреляция глубинности минералов с величинами их удельной массовой энергии атомизации по Э. Мамырову (Мамыров, 1989).
Приведем также ряд других примеров прикладного использования параметров γ. По данным (Смольянинов, 1955) флюорит легко и иногда в больших количествах замещает кальцит, что можно связать с ростом γ в этом процессе:
CaCO3 (γ = 0,65) → CaF2 (γ = 1,0).
Аналогичным образом объясняется легкость замещения галенита англезитом:
PbS (γ = 1,0) → PbSO4 (γ = 1,22).
Можно констатировать, что в зоне окисления многие процессы замещения одних минералов другими сопровождаются уплотнением вновь образующихся кристаллических решеток минералов, что связано с ростом параметров γ. Повышенная устойчивость малахита по сравнению с азуритом может служить тому примером:
Азурит Cu3[CO3]2(OH)2 (γ = 0,45) → малахит Cu2[CO3](OH)2 (γ = 0,74).
Сульфид меди, например, халькопирит CuFeS2 (γ = 0,65), в зоне окисления замещается ковеллином CuS (γ = 0,69), купритом Cu2O
(γ = 0,49), самородной медью Cu (γ = 1,42), гетитом FeOOH (γ = 0,76). Как видим, параметры γ указанных продуктов замещения халькопирита заметно растут по отношению к исходной величине γ.
В качестве выводов по данному разделу можно заключить, что кристаллохимические параметры структурной плотности минералов γ определенно коррелируются с условиями (глубинностью) минералообразования, а также могут служить индикаторами (указателями) направленности процессов замещения одних минералов другими.
[1] Точнее, n есть число самостоятельных структурных узлов кристаллической решетки, включая атомы, ионы и радикалы (комплексные ионы).
Быстрое оформление заказа
Рассчитать количество материала
Оставьте контактные данные и мы перезвоним вам в ближайшее время
Оформление заказа
Физическое лицо / ИП
Юридическое лицо
✕
Спасибо за вашу заявку!
Мы скоро вам перезвоним
Рассчитать количество материала
Спасибо за заявку!
Ожидайте звонка нашего специалиста
1.6.3. Плотность кристаллических структур
В расчетах на прочность лопатки турбины необходимо знать плотность материала. В частности, ее величину для матрицы и армирующей фазы эвтектического композита лопатки, чтобы оценить величину объемных сил инерции при вращении рабочего колеса турбины. Решение данной задачи является одним из этапов обобщенной модели прочности лопатки [41] (рис. 1.39).
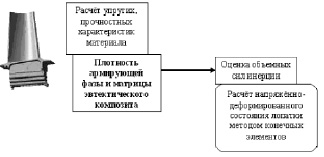
Рис. 1.39
В данном разделе обосновывается расчет плотности монокристаллов.
Плотность монокристаллов r определяется по известной формуле
r = m/V,
где m – масса; V – объем.
В рассматриваемом случае в качестве объема принимается объем элементарной атомной ячейки с периодом кристаллической решетки a0, равный
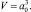
Масса элементарного объема определяется по следующей формуле:
m = mАMедkр,
где mА – атомная масса элемента; Mед = 1,66⋅10–27 кг – атомная единица массы; kр – коэффициент ретикулярной плотности для элементарной атомной ячейки (рис. 1.40).
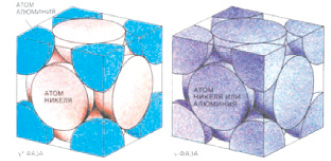
Рис. 1.40. Схема формирования ретикулярной плотности в ячейке [42]
Коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры определяется в соответствии с правилами кристаллографии [43].
Тогда формула расчета плотности монокристалла, разработанная автором, примет следующий вид [44]
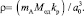
Плотность монокристалла простого вещества, состоящего из атомов одного химического элемента железа – Fe с объемно-центрированной кристаллической решеткой, определяется как
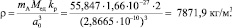
Плотность монокристалла простого вещества, состоящего из атомов одного химического элемента меди – Cu с гранецентрированной кристаллической решеткой, определяется как
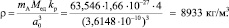
Плотность сложных веществ или соединений, состоящих их атомов разных химических элементов типа NaCl, определяется как сумма плотностей составляющих химических элементов, т.е.
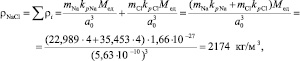
где kрNa, kрCl – коэффициент ретикулярной плотности соответственно для Na и Cl; mNa, mCl – атомная масса соответственно для Na и Cl; a0 – период кристаллической решетки NaCl (табл. 1.20).
Таблица 1.20
|
Символ элемента, |
Величина плотности r, кг/м3 |
Расхождение, % |
|
|
расчетная |
экспериментальная |
||
|
Fe |
7871,9 |
7872 |
0 |
|
Cu |
8933 |
8933 |
0 |
|
NaCl |
2174,5 |
2100 |
3,5 |
Из табл. 1.20 видно, что расчетная величина плотности для железа Fe составляет 7871,9 кг/м3, а экспериментальное значение – 7872 кг/м3 [7].
Результаты некоторых расчетов плотности приведены в табл. 1.21.
Таблица 1.21
|
Наименование |
Величина плотности, кг/м3 |
Погрешность, % |
Источник |
|
|
расчетная |
экспериментальная |
|||
|
Mo (ОЦК) |
10219,9 |
10218 (10200) |
0,02 |
[7] |
|
W (ОЦК) |
19248,5 |
19263 (19230) |
0,08 |
[7] |
|
Ta (ОЦК) |
16678,6 |
16623 (16600) |
3,3 |
[7] |
|
Nb (ОЦК) |
8581,5 |
8630 (8570) |
5,6 |
[7] |
|
TaС (кубич) |
14625,0 |
14500 |
8,6 |
[7] |
Примечание. Приведены рентгеновская и пикнометрическая (в скобках) экспериментальные значения плотности.
Как видно из табл. 1.20, 1.21, результаты расчетов удовлетворительно сходятся с результатами экспериментов.
Таким образом, результаты расчета применимы для оценки плотности моно- и поликристаллов, в том числе соединений, по которым редко или совсем не встречается справочная информация.
Результаты расчета плотности моно- и поликристаллов, из которых состоит матрица эвтектических композитов, являются исходными данными для моделирования прочности лопаток газовых турбин.
Страницы работы
Содержание работы
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПО ТЕМАМ ЧАСТИ №1
«СТРОЕНИЕ И СВОЙСТВА ТВЁРДЫХ ТЕЛ. КВАНТОВЫЕ
СТАТИСТИКИ»
Тема 1. Строение стёрдых тел
Основные формулы
1. Объем элементарной ячейки в кристаллах:
а) кубической
сингонии
![]() ,
,
б) гексагональной
сингонии
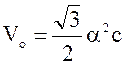 ,
,
где ![]() и с – параметры решетки.
и с – параметры решетки.
2.
Период решетки (расстояние между
ближайшими одноименными ионами)
а) объемоцентрированной
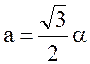 ,
,
б) гранецентрированной
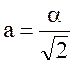 .
.
3.
Объем одного моля кристалла
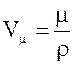 ,
,
где m – масса моля кристалла, r – его плотность.
4.
Число элементарных ячеек в одном
моле кристалла
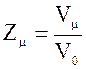 или
или 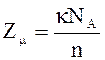 ,
,
где k -одинаковое число атомов в
химической формуле соединения, NA – число Авогадро, n – число
одинаковых атомов, приходящихся на элементарную ячейку.
5.
Число элементарных ячеек в единице
объема кристалла
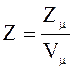 или в общем случае
или в общем случае 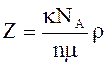 .
.
В качестве индексов узлов кристаллической решетки
принимается совокупность величин Х/а, У/в, Z/с,
обозначаемых [[m n p]].
6.
Индексы направления в
кристаллической решетке определяются наименьшими числами m, n, p,
пропорциональными индексам любого узла, через который проходит прямая:
m : n : p = Х/а : У/в : Z/с.
Индексы направления заключаются в одинарные скобки [m n p ].
7. Миллеровские индексы плоскости задаются с помощью
наименьших чисел h, k, l, обратных отрезкам u, v, w,
отсекаемых плоскостью на координатных осях. Индексы плоскости записываются в
круглых скобках (hkl).
9. Уравнение Вульфа-Брэггов для дифракции
рентгеновского излучения на кристаллах имеет вид:
![]() ,
,
где d – межплоскостное расстояние, Q – угол скольжения, k –
порядок дифракционного максимума.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1 .Сколько
атомов приходится на одну элементарную ячейку объемоцентрированной кубической
решетки?
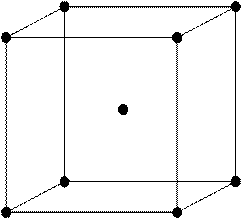 |
Рис. 1
Решение:
Элементарная ячейка
объемоцентрированной кубической решетки изображена на рис. 1. В этой ячейке
имеются узлы кристаллической решетки двух типов: узлы, находящиеся в вершинах
куба, и узел, находящийся на пересечении двух пространственных диагоналей куба.
Каждый узел в вершинах принадлежит одновременно восьми элементарным ячейкам.
Следовательно, на данную элементарную ячейку приходится 1/8 узла. Находящийся
на пересечении диагоналей узел целиком находится в ячейке. Так как вершин
восемь, то на одну элементарную ячейку в объемоцентрированной решетке
приходится всего атомов
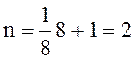 .
.
Задача 2. Определить
плотность кристалла стронция, если известно, что он имеет кристаллическую
решетку гранецентрированной кубической сингонии, а период решетки d =
0,43 нм.
Дано: d = 0,43 нм, А = 87,6 кг/катом. Определить r.
Решение: Плотность
кристалла стронция можно определить по формуле
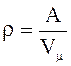 .
.
(1)
Выразим объем одного моля кристалла Vm через объем элементарной
ячейки V0,
воспользовавшись соотношением
Vm = V0 Zm.
Но Zm = NA/n, а V0 = a3, где а – параметр
решетки. Для гранецентрированной ячейки
а = Ö2 d и V0 = 2Ö2 d3.
На гранецентрированную ячейку приходится n = 4
атома. После подстановки указанных выше соотношений в формулу (1) окончательно
для плотности кристалла получим выражение
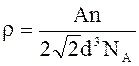 .
.
Подставим числовые значения:
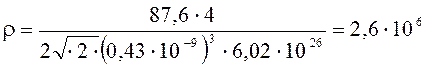 кг/ м3.
кг/ м3.
Задача
3. На грань кристалла каменной соли
падает параллельный пучок рентгеновских лучей с длиной волны 0, 147 нм.
Определить расстояние меэду атомными плоскостями кристалла, если дифракционный
максимум второго порядка наблюдается, когда лучи падают на кристалл под углом
31030/.
Дано: l= 0,147 нм = 1,47 10-10 м; j = 31030/ ; k = 2.
Определить d.
Решение: Запишем уравнение Вульфа-Брэггов
![]() .
.
Угол q является дополнительным к углу j.
q= p/2 – j = 58030/.
Межплоскостное расстояние d определим из
выражения
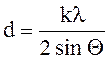 .
.
Подставим числовые значения:![]()
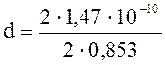 = 1,7 10-10 м = 0,17 нм.
= 1,7 10-10 м = 0,17 нм.
Тема 2. Тепловые свойства твердых тел
Основные формулы
1. Теплоемкость одного моля химически простых
твердых тел определяется по закону Дюлонга и Пти
![]() ,
,
где R – универсальная газовая постоянная.
2.
Теплоемкость одного моля химически
сложных тел определяется по закону Неймана – Коппа
![]() ,
,
где n – общее число частиц в химической формуле.
3.
Среднее значение квантового
осциллятора, приходящаяся на одну степень свободы, в квантовой теории
Эйнштейна:
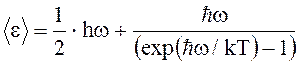 ,
,
где ![]()
![]() –
–
нулевая энергия, ![]() – перечеркнутая постоянная
– перечеркнутая постоянная
Планка, w – циклическая частота, k – постоянная Больцмана, Т – абсолютная температура.
4.
Внутренняя энергия одного моля
кристалла в квантовой теории теплоемкости Эйнштейна
Похожие материалы
- Задачи для самостоятельного решения по темам части № 1 «Строение и свойства твёрдых тел, квантовые статистики»
- Задания для самоподготовки к итоговому тестированию по темам части № 2 «Металлы, полупроводники, диэлектрики»
- Примеры решения задач по теме № 5 «Физика колебаний и волн»
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Изобретение относится к области испытания физических свойств материалов и предназначено для определения плотности. Технический результат изобретения – расширение функциональных возможностей, снижение трудоемкости за счет прогнозирования физических свойств материала расчетом по формуле. Сущность изобретения заключается в том, что для монокристаллов простых веществ определяют период кристаллической решетки рентгеноструктурным методом, а затем вычисляют плотность по установленной формуле, а для монокристаллов сложных веществ определяют период кристаллической решетки рентгеноструктурным методом, затем по установленной формуле определяют плотность каждого составного химического элемента ρi в элементарной ячейке кристаллической структуры сложного вещества, после чего плотность сложного вещества ρ определяют как сумму плотностей простых веществ, входящих в состав сложного вещества. 2 н.п. ф-лы, 1 табл.
Изобретение относится к способам определения плотности твердых тел.
Известен способ определения плотности твердых тел, включающий, в частности, погружение исследуемого тела в сосуд с жидкостью, предварительное измерение среднего диаметра и измерение скорости погружения (Авторское свидетельство СССР №1698705, М. Кл. G 01 N 9/00, 15.12.1991 г.).
Известен способ определения кажущейся плотности пористых изделий, включающий, в частности, физическое воздействие на изделие, определение параметра, с учетом которого по тарировочным графикам определяют плотность (Авторское свидетельство СССР №1820302, М. Кл. G 01 N 9/00, 07.06.1993 г).
Известен способ определения истинной плотности порошковых материалов, включающий, в частности, измерение модуля упругости исследуемого материала путем механического нагружения в упругой области образцов (Авторское свидетельство СССР №1827582, М. Кл. G 01 N 9/00, 15.07.1993 г.).
Недостатками способов являются ограниченные функциональные возможности.
Наиболее близким по достигаемому результату является способ, по которому производится последовательное взвешивание исследуемого тела, отбор материала из анализируемой части объема и определение плотности по формуле (Авторское свидетельство СССР №1723497, М. Кл. G 01 N 9/00, 30.03.1992 г.).
Недостатками являются трудоемкость способа и ограниченные функциональные возможности.
Технический результат изобретения снижение трудоемкости способа, возможность прогнозирования плотности материала путем расчета по формуле, а также расширение функциональных возможностей за счет определения плотности предельно малых объемов на уровне нанометрических размеров.
Технический результат изобретения достигается за счет того, что в способе определения плотности твердых тел, по которому плотность вычисляют по формуле, в отличие от прототипа для монокристаллов простых веществ определяют период кристаллической решетки рентгеноструктурным методом, а затем по формуле
ρ=(mAMедkр)/а0 3,
где mA – атомная масса элемента;
Мед = 1,66·10-27 кг – атомная единица массы;
kp – коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры;
а0 – период кристаллической решетки
определяют плотность.
К тому же технический результат изобретения достигается за счет того, что в способе определения плотности твердых тел, по которому плотность вычисляют по формуле, в отличие от прототипа для монокристаллов сложных веществ определяют период кристаллической решетки рентгеноструктурным методом, а затем по формуле
ρ=(mAMедkр)/а0 3,
где mA – атомная масса элемента;
Мед = 1,66·10-27 кг – атомная единица массы;
kp – коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры;
а0 – период кристаллической решетки
определяют плотность каждого составного химического элемента ρi в элементарной ячейке кристаллической структуры сложного вещества, после чего плотность сложного вещества ρ определяют как сумму плотностей простых веществ, т.е.
ρ=Σρi,
где i – номер химического элемента, входящего в состав сложного вещества.
Кроме того, период кристаллической решетки можно определить по справочным данным (Кристаллография и дефекты кристаллической решетки. Учебник для вузов / Новиков И.И., Розин К.М. М.: Металлургия, 1990, 336 с.).
Пример конкретной реализации способа
Для рентгеноструктурного анализа изготавливаются образцы. Монолитные образцы в форме шлифов изготавливают из исследуемого материала обычными механическими способами и перед съемкой подвергают электролитической полировке для снятия наклепа. Плоские шлифы подготавливают для съемки с помощью электролитического травления для снятия деформированного слоя. При съемке на просвет образцы должны электролитически утоньшаться до тонкой фольги.
Для определения периодов кристаллической решетки необходимо измерить межплоскостные расстояния, проиндицировать дифракционные отражения и, зная связь между межплоскостным расстоянием, индексами отражающих плоскостей и периодами решетки, рассчитать последние (С.С.Горелик, Л.Н.Расторгуев, Ю.А.Скаков Рентгенографический и электронно-оптический анализ. М.: Металлургия, 1970, 366 с.).
Методами прецизионного определения периода кристаллической решетки могут служить следующие:
– асимметричная съемка с расчетом по последним линиям;
– метод съемки на больших расстояниях в широком расходящемся пучке;
– метод съемки с независимым эталоном;
– безэталонный метод при обратной съемке и др.
Выбор того или иного метода определения периода решетки связан с расположением линий на рентгенограмме и симметрией решетки исследуемого материала (Н.Н.Качанов, Л.И.Миркин Рентгеноструктурный анализ. М.: Машгиз, 1960, 216 с.).
Коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры определяется в соответствии с правилами кристаллографии [Лахтин Ю.М., Леонтьев В.П. Материаловедение: Учебник для ВУЗов – 3-е изд., – М.: Машиностроение, 1990. – 528 с].
Например, плотность монокристалла простого вещества, состоящего из атомов одного химического элемента железа Fe с объемно-центрированной кристаллической решеткой, определяется как
ρ=(mAMедkр)/а0 3=(55,847·1,66·10-27·2)/(2,8665·10-10)3=7871,9 кг/м3.
Плотность монокристалла простого вещества, состоящего из атомов одного химического элемента меди – Cu с гранецентрированной кристаллической решеткой, определяется как
ρ=(mAMедkр)/а0 3=(63,546·1,66·10-27·4)/(3,6148·10-10)3=8933 кг/м3.
Плотность сложных веществ или соединений, состоящих их атомов разных химических элементов типа NaCl, определяется как сумма плотностей составляющих химических элементов, т.е.
ρNaCl=ΣρI=(mNakpNaМед)/a0 3+(mClkpClМед)/а0 3=((mNakpNa+mClkpCl)Мед)/а0 3=((22,989·4+35,453·4)·1,66·10-27)/(5,63·10-10)3=2174 кг/м3,
где kpNa, kpCl – коэффициент ретикулярной плотности соответственно для Na и Cl;
mNa, mCl – атомная масса соответственно для Na и Cl;
а0 – период кристаллической решетки NaCl.
| Таблица | |||
| Символ элемента или соединения | Величина плотности ρ, кг/м3 | ||
| расчетная | экспериментальная | погрешность % | |
| Fe | 7871,9 | 7872 | 0 |
| Cu | 8933 | 8933 | 0 |
| NaCl | 2174,5 | 2100 | 3,5 |
Из таблицы видно, что расчетная величина плотности для железа Fe составляет 7871,9 кг/м3, а экспериментальное значение – 7872 кг/м3 (Свойства элементов. В двух частях, 4.1. Физические свойства. Справочник. Второе изд. М., Металлургия, 1976. 600 с.).
Таким образом, заявляемое изобретение позволяет снизить трудоемкость за счет расчета по формуле, в свою очередь, определение плотности предельно малых объемов на уровне нанометрических размеров расширяет функциональные возможности способа.
1. Способ определения плотности твердых тел, по которому плотность вычисляют по формуле, отличающийся тем, что для монокристаллов простых веществ определяют период кристаллической решетки рентгеноструктурным методом, а затем по формуле
ρ=(mAMедkр)/а0 3,
где mA – атомная масса элемента;
Мед=1,66·10-27 кг – атомная единица массы;
kp – коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры;
а0 – период кристаллической решетки,
определяют плотность.
2. Способ определения плотности твердых тел, по которому плотность вычисляют по формуле, отличающийся тем, что для монокристаллов сложных веществ определяют период кристаллической решетки рентгеноструктурным методом, а затем по формуле:
ρ=(mAMедkр)/а0 3,
где mA – атомная масса элемента;
Мед=1,66·10-27 кг – атомная единица массы;
kp – коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры;
а0 – период кристаллической решетки,
определяют плотность каждого составного химического элемента ρi в элементарной ячейке кристаллической структуры сложного вещества, после чего плотность сложного вещества ρ определяют как сумму плотностей простых веществ, т.е.:
ρ=Σρi,
где i – номер химического элемента, входящего в состав сложного вещества.