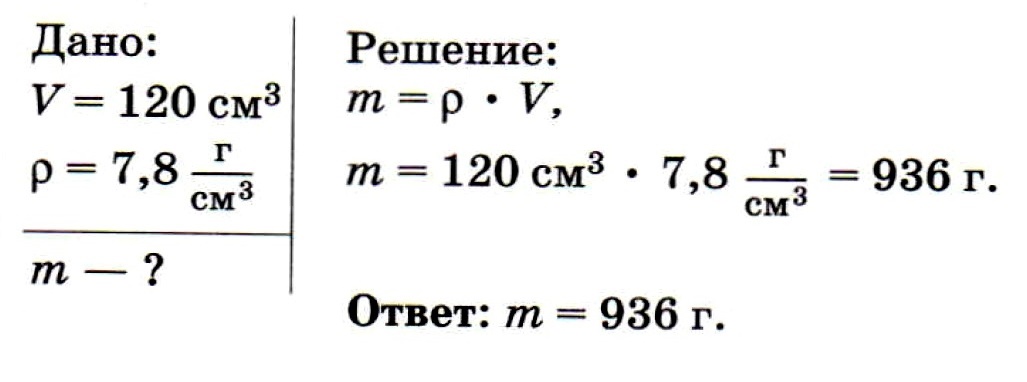Как найти плотность материала куба

Задачи на плотность, массу и объем с решением

Формулы, используемые по теме «Задачи на плотность, массу и объем с решением»

Название величины	Обозначение	Единицы измерения	Формула
Масса	m	кг	m = ρ * V
Объем	V	м3	V = m / ρ
Плотность	ρ	г/см3, кг/м3	ρ = m / V

Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Найдите плотность молока, если 206 г молока занимают объем 200 см³?

---

Задача № 2.
 Определите объем кирпича, если его масса 5 кг?

---

Задача № 3.
 Определите массу стальной детали объёмом 120 см³

---

Задача № 4.
 Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?

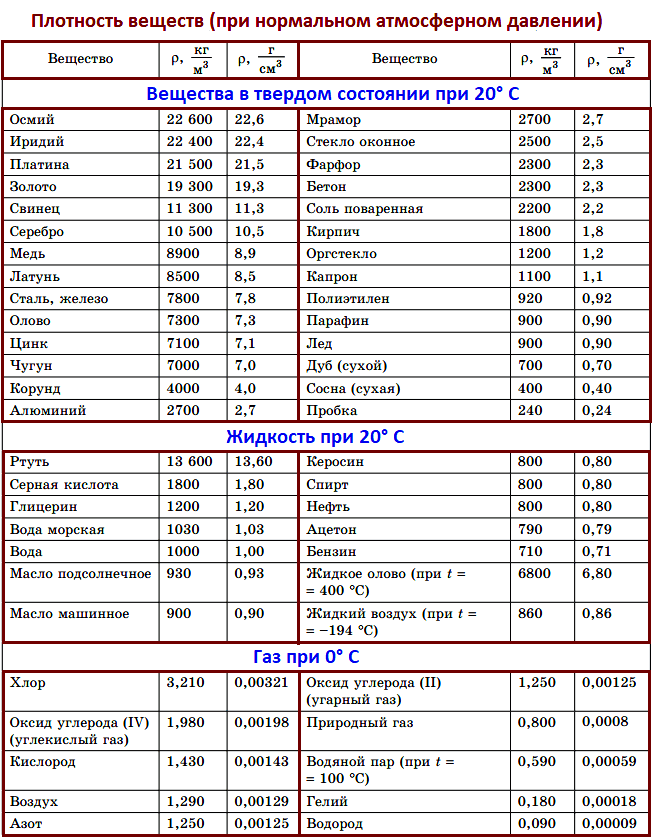
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ₂ = 7000 кг/м³) меньше плотности стали (ρ₁ = 7800 кг/м³). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.

---

Задача № 5.
 Определите плотность мела, если масса его куска объемом 20 см³ равна 48 г. Выразите эту плотность в кг/м³ и в г/см³.

Ответ: Плотность мела 2,4 г/см³, или 2400 кг/м³.

---

Задача № 6.
 Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м² ?

ОТВЕТ: 160 кг.

Указания к решению. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м³ • 0,04 м² • 5 м = 160 кг.

---

Задача № 7.
 Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.

ОТВЕТ: Брусок сделан из алюминия.

---

Задача № 8 (повышенной сложности).
 Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?

ОТВЕТ: 5 мм.

---

Задача № 9 (олимпиадный уровень).
 Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.

ОТВЕТ: 8000 кг/м³

Задачи на плотность,
массу и объем с решением

---

Справочный материал для
«Задачи на плотность, массу и объем«

Таблица плотности веществ.

Как, зная только массу, рассчитать плотность?

1. Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
2. Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
3. Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
4. Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
5. Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
6. Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
7. Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.

---

Задачи на плотность,
массу и объем с решением

ВОПРОСЫ ОТ ПОЛЬЗОВАТЕЛЕЙ САЙТА

Публикуем популярные вопросы от наших пользователей, оставленные в поле Комментариев. Прежде чем написать свой вопрос, проверьте: нет ли похожей задачи в начале статьи в разделе «Примеры решения задач» или среди вопросов в данном разделе!

Вопрос № 1. Длина стального листа 120 см, ширина 60 см, толщина 10 мм. Определить массу одного листа.

ОТВЕТ:≈ 56 кг.

Вопрос № 2. Какова масса платинового стержня, объём которого равен 21 дм³ ?

ОТВЕТ: 451,5 кг.

Вопрос № 3. Определить плотность бензина, если бак с бензином ёмкостью 20 литров имеет массу 14,2 кг?

Ответ: 710 кг/м³

Вопрос № 4. Масса бетонного блока, имеющего форму параллелепипеда, равна 12 кг. Какой станет масса блока, если одну его сторону увеличить в 2 раза, вторую – в 2,5 раза, а третью оставить без изменения?

ОТВЕТ: 60 кг.

Вопрос № 5. Сколько рейсов должен сделать самосвал грузоподъемностью 5 т, чтобы перевезти 100 м³ гранита? Плотность гранита 2600 кг/м³.

ОТВЕТ: 52 рейса.

Вопрос № 6. Плотность некоторого раствора 1300 кг/м³. После того как в этот раствор добавили 10 л воды (деминерализованной) плотность этого раствора стала 1290 кг/м³. Сколько литров раствора было с исходной плотностью?

ОТВЕТ: 290 литров.

---

Конспект урока по физике в 7 классе «Задачи на плотность, массу и объем с решением». Выберите дальнейшие действия:

• Перейти к теме: «ЗАДАЧИ на силу тяжести и вес тела».
• Вернуться к Списку конспектов по физике для 7-11 классов
• Найти конспект через Кодификатор ОГЭ по физике
• Найти конспект через Кодификатор ЕГЭ по физике

Unit Converter

Enter the cube mass (kg), the cube length (m), and the cube width (m), and cube height (m) into the Cube Density Calculator. The calculator will evaluate and display the Cube Density. 

• All Density Calculators
• Weight to Density Calculator
• Liquid Density Calculator
• Mass to Density Calculator

Cube Density Formula

The following formula is used to calculate the Cube Density. 

Dcube = CM / (L*W*H)

• Where Dcube is the Cube Density (kg/m^3)
• CM is the cube mass (kg) 
• L is the cube length (m) 
• W is the cube width (m) 
• H is the cube height (m)

How to Calculate Cube Density?

The following example problems outline how to calculate Cube Density.

Example Problem #1

1. First, determine the cube mass (kg).
   1. The cube mass (kg) is given as 400.
2. Next, determine the cube length (m). 
   1. The cube length (m) is calculated as: 5.
3. Next, determine the cube width (m). 
   1. The cube width (m) is found to be: 6.
4. Next, determine the cube height (M).
   1. For this problem, the height is 3m.
5. Finally, calculate the Cube Density using the formula above: 

Dcube = CM / (L*W*H)

Inserting the values from above yields: 

Dcube = 400/ (5*6*3) = 4.44 (kg/m^3)

Подпишись на наш канал в телеграм. Там мы даём ещё больше полезной информации для школьников!

Решение
задач на нахождение плотности смесей и сплавов,

средней
плотности неоднородных тел (7 класс)

Ларионов Вадим Сергеевич,

 учитель физики МБОУ Лицея №
15 г.Сарова, larionvadim@yandex.ru

Ларионова Наталья Валентиновна,

к.п.н., учитель физики МБОУ Лицея № 15
г.Сарова, nvlarionova@yandex.ru

В статье сформулированы методические рекомендации по
организации факультативного занятия по решению задач на нахождение плотности
смесей, сплавов и неоднородных тел. Представлены учебные материалы по теме,
структурированные по уровню сложности.

Задачи на
нахождение плотности смеси или сплава, средней плотности неоднородного
(«составного»)  тела являются базовыми при изучении темы «Плотность»  и
достаточно часто встречаются в олимпиадах по физике в 7-8-х классах. Именно
поэтому целесообразно данному типу задач посвятить отдельное факультативное занятие,
структура которого соответствует принципу «от простого к сложному» и содержит последовательные
блоки задач: ключевые, олимпиадные и задачи для самостоятельного решения (см.
приложение).

Средняя плотность
неоднородного («составного») тела, плотность смеси или сплава рассчитывается по
формуле

где m₁, m₂, m₃… -массы отдельных частей тела
(компонентов смеси или сплава), а V₁, V₂, V₃ … – их объёмы.

Для решения задач
по данной теме,  необходимо составить систему уравнений, в основе которой лежат
следующие положения:

1.       Определительная формула
плотности

2.       Свойство аддитивности массы
(масса смеси или сплава равна сумме масс его составных частей)

m=m₁+ m₂+ m₃+…

3.       Как правило, в таких задачах
полагают, что объём сплава (смеси) равен сумме объёмов его составных частей

V=V₁+V₂+V₃ …

В задачах, предложенных ниже,
исключением является задача № 6 из блока олимпиадных задач (задача о смешивании
спирта и воды).

Ключевые задачи,
представленные в занятии, в зависимости от подготовки учащихся могут быть
решены непосредственно на уроке при изучении темы «Плотность». В этом случае на
факультативном занятии рассматриваются олимпиадные задачи. Далее ученикам
предлагаются задачи для самостоятельного решения, которые, как правило,
составляют домашнее задание. В этом случае удобно дифференцировать домашнее
задание учеников, предложив не более трёх обязательных задач в зависимости от
уровня подготовленности учеников. Учитель может дополнить списки олимпиадных
задач и задач для самостоятельного решения, используя материалы последних
олимпиад.

Приложение

Плотность смесей, сплавов, «составных» тел

Цель:  Научиться решать задачи
на нахождение плотности смесей и сплавов, а также средней плотности
неоднородных тел («составных») тел.

Ключевые задачи

1.       Какова плотность сплава из
300г олова и 100г свинца? (8г/см³)

2.                    
Сплав
изготовлен из меди объёмом 0,4 м³  и цинка массой 710 кг. Какова
плотность сплава? (8540 кг/м³)

3.       Для приготовления вишнёвого
сиропа в кастрюлю вылили 1 л вишнёвого варенья и 2 л воды и хорошо перемешали.
Какова плотность сиропа, если плотность варенья 1300 кг/м³? (1100
кг/м³)

4.       Какова плотность смеси из
глицерина и спирта, если объём спирта составляет половину объёма смеси? Как
изменится ответ, если масса спирта составляет половину массы смеси? (1030 кг/м³, 980 кг/м³)

Олимпиадные задачи

1.       Масса первого изделия в 2
раза больше массы второго изделия, а их объёмы находятся в отношении V₁:V₂=1:3. Плотность первого изделия ρ₁=4г/см³.
Какова будет средняя плотность «составного» тела, если два изделия склеить?
Массой и объёмом клея пренебречь. (1,5 г/см³)

2.       Изделие, склеенное из трёх
различных частей, имеет объём V=600см³.
Объёмы частей находятся в соотношении V₁:V₂:V₃=2:3:5, а их плотности – в соотношении ρ₁:ρ₂:ρ₃=4:3:1.
Чему равна масса изделия, если плотность первой части ρ₁=2000кг/м³?
(660 г)

3.       Ученик измерил плотность
деревянного бруска, покрытого краской, и она оказалась равной ρ=600 кг/м³. Но на
самом деле брусок состоит из двух частей, равных по массе, плотность одной из
которых в два раза больше плотности другой. Найдите плотности обеих частей
бруска. Массой краски можно пренебречь. (450 кг/м³, 900 кг/м³)

4.       В дистиллированную воду
аккуратно вливают серную кислоту. Получившийся раствор имеет плотность ρ_р=1200
кг/м³ и массу m=120г. Объём раствора равен
сумме объёмов воды и кислоты. Плотность воды ρ_в=1000 кг/м³,
плотность кислоты ρ_к=1800 кг/м³.  Какова масса кислоты,
влитой в воду? (45 г)

5.       Однородный кубик со стороной
a и плотностью ρ поместили внутрь куска глины с плотностью 4ρ, которому придали
форму куба со стороной 2a. Получившийся куб облепили пластилином плотностью 2ρ,
в результате чего получился куб со стороной 3a (см. рисунок). Определите
среднюю плотность получившейся системы. (67ρ/27≈2,5ρ)

6.       Плотностью вещества называют
отношение массы тела из этого вещества к его объёму. Например, масса 1 см³
воды составляет 1 г, поэтому плотность воды 1 г/см³. Представим, что
смешали 100 литров воды и 100 литров спирта плотностью 0,8 г/см³, и
при смешении оказалось, что суммарный объём уменьшился на 5 процентов. Какова
плотность полученного раствора? (ρ=18/19 г/cм³≈0,95г/cм³)

Задачи
для самостоятельного решения

1.   Какую плотность имеет сплав
из 270г алюминия и 445г меди? (≈4,77
г/cм³)

2.   Сплав золота и серебра массой
400 г имеет плотность 1,4·10⁴ кг/м³. Полагая объём сплава
равным сумме объёмов его составных частей, определите массу золота в сплаве? (220
г)

3.   Масса первого изделия в 3
раза меньше массы второго изделия, а их объёмы находятся в соотношении V₁:V₂=2:1. Плотность первого тела ρ₁=1,8 г/см³.
Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой
и объёмом клея пренебречь. (4,8 г/см³)

4.   Изделие, склеенное из трёх
различных частей, имеет объём V=900см³.
Объёмы частей находятся в соотношении V₁:V₂:V₃=5:3:1, а их плотности – в соотношении ρ₁:ρ₂:ρ₃=1:2:5.
Чему равна масса изделия, если плотность первой части ρ₁=500кг/м³?
(800 г)

5.       Кубик с ребром a=20см сделан из материала с
плотностью ρ=3000кг/м³. Однако внутри кубика имеется воздушная
полость, поэтому его средняя плотность ρ_ср=1200кг/м³.
Определите объём этой воздушной полости. Во сколько раз изменится средняя
плотность кубика, если полость целиком заполнить водой? Массой воздуха внутри
полости можно пренебречь. (4800 см³, 1,5)

Литература к занятию

1.     Генденштейн Л.Э., Кирик Л.А.,
Гельгафт И.М. Задачи по физике с примерами решений. 7-9 классы. Под ред. В.А.Орлова.
– М.: Илекса, 2009. – 416 с.

2.       Бажанский И.И., Гой В.А.,
Чубов Ю.Б. Приморские олимпиады школьников по физике (2003-2007 гг). Учебное
пособие. – Владивосток: Изд-во Дальневост. ун-та, 2008. – 200с.

3.       Олимпиады 2008-2009. Физика.
Задачи Московских олимпиад школьников. Под ред. М.В.Семёнова, А.А.Якуты. – М.:
МЦНМО, 2009. – 70 с.

4.       400 физических этюдов.
Избранные задачи физических олимпиад Санкт-Петербурга. – СПб, 2006. –284 с.

5.       
Борисов
С.Н. Учебное пособие по физике для учащихся 7-го класса. – М.: МИФИ, 2009.  –
100 с.