Как найти плотность материала шара

Условие задачи:

В воде плавает шар, погрузившись на 0,25 своего объема. Определить плотность материала шара.

Задача №3.3.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(V_{п}=0,25V), (rho-?)

Решение задачи:

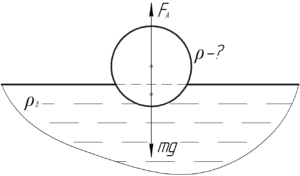Если шар плавает, значит сила Архимеда равна силе тяжести:

[{F_А} = mg]

Силу Архимеда находят по формуле:

[{F_А} = {rho _в}g{V_п}]

В этой формуле (rho_{в}) – плотность воды (жидкости, в которую погружен шар), (V_{п}) – объем погруженной части шара.

Массу шара можно найти как произведение плотности материала шара (rho) на его полный объем (V).

[m = rho V]

Тогда имеем:

[{rho _в}g{V_п} = rho Vg]

[{rho _в}{V_п} = rho V]

Так как по условию (V_{п}=0,25V), то:

[{rho _в} cdot 0,25V = rho V]

В итоге:

[rho  = 0,25{rho _в}]

Плотность воды равна 1000 кг/м³, поэтому плотность материала, из которого изготовлен шарик, равна:

[rho  = 0,25 cdot 1000 = 250;кг/м^3 = 0,25;г/см^3]

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.2.24 С какой силой давит атмосферный воздух на обложку книги размером 12×20 см2
3.3.2 Брусок дерева плавает в воде. Объем погруженной части бруска 36 см3. Определить
3.3.3 Льдина плавает на поверхности воды. Часть её объема, равная 150 м3, находится

Плотность является полезной характеристикой. Каждый материал имеет характерную плотность, и ни один из них не является одинаковым, поэтому вы можете использовать плотность в качестве метода идентификации. Вот как Архимеду удалось определить, была ли корона, подаренная ему королем, сделана из золота или нет.

Плотность определяется как масса на единицу объема, что означает, что если вы хотите рассчитать плотность чего-либо, вы должны измерить его массу, а затем рассчитать его объем. Формула плотности

rho = frac {m} {V}

где ρ – плотность, m – масса, а V – объем материала.

Расчет объема прост для обычных фигур, таких как кубы, прямоугольники и пирамиды, потому что все, что вам нужно сделать, это измерить размеры и использовать формулу. Это также верно для сфер.

Как рассчитать объем сферы

Формула для объема сферы: 4/3 × π_r_ ³, где r – радиус сферы. Это довольно просто, за исключением того, что на практике может быть сложно измерить радиус. Даже если у вас есть масштабированная двухмерная проекция сферы, с которой можно работать, все еще может быть трудно точно определить центр.

Обычно легче измерить диаметр, который равен удвоенному радиусу. Это означает, что r = d / 2, поэтому после выполнения арифметики вы можете переписать формулу объема в терминах диаметра следующим образом:

V = frac {1} {6} × πd ^ 3

Масса сферы против веса

Всегда есть небольшая путаница между массой и весом. Масса, которая является величиной, необходимой для определения плотности, является неотъемлемым сопротивлением тела к изменению движения, но вес – это сила, оказываемая гравитацией на тело. Масса может быть измерена в килограммах, но вес измеряется в ньютонах. В имперской системе единица измерения массы – слизняки, а вес измеряется в фунтах.

Соглашение состоит в том, чтобы взвешивать объекты в килограммах в системе СИ, которые являются единицами массы, и в фунтах в имперской системе, которые являются единицами веса. Выполняя измерения на поверхности Земли, обычно безопасно игнорировать эти различия, но не в космосе, где сила гравитации различна.

Расчет плотности сферы

После того, как вы взвесите сферу, у вас будет значение m . Теперь все, что вам нужно сделать, это рассчитать его объем ( V ), что вы можете сделать, если измерить его диаметр, d . Формула плотности ρ = m / V , и вы можете изменить эту формулу объема, чтобы выразить соотношение через d :

begin {align} rho & = frac {m} {(1/6) × πd ^ 3} & = frac {6m} {πd ^ 3} end {выровненный}

Использование плотности для расчета массы или объема сферы

Предположим, у вас есть пушечное ядро, сделанное полностью из железа. Вы можете посмотреть плотность железа в таблице: 7, 8 г / см ³. Вы взвешиваете пушечное ядро ​​и обнаруживает, что оно весит 20 фунтов. Теперь у вас есть достаточно информации, чтобы рассчитать его объем, поэтому просто измените формулу плотности для V: V = m / ρ .

Есть только одна проблема. Плотность в метрических единицах CGS, а вес в имперских единицах. В зависимости от того, хотите ли вы указать объем в метрических или имперских единицах, вы можете либо перевести вес в килограммы, либо посмотреть плотность в фунтах на кубический дюйм. Используйте любое из этих преобразований:

1 ; text {lb} = 0.45359 ; text {kg, so} 20 ; text {lbs} = 9.07 ; text {kg} 7.8 ; text {г / см} ^ 3 = 0, 28 ; text {фунт / дюйм} ^ 3

Кроме того, вы можете рассчитать вес (массу) пушечного ядра, если вы можете измерить его диаметр. Используйте эту формулу:

m = frac {1} {6} rhoπd ^ 3

Масса

Бозон Хиггса невозможно представить. Это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.

Объем тела

Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Это важный навык — уметь объемы соотносить. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.

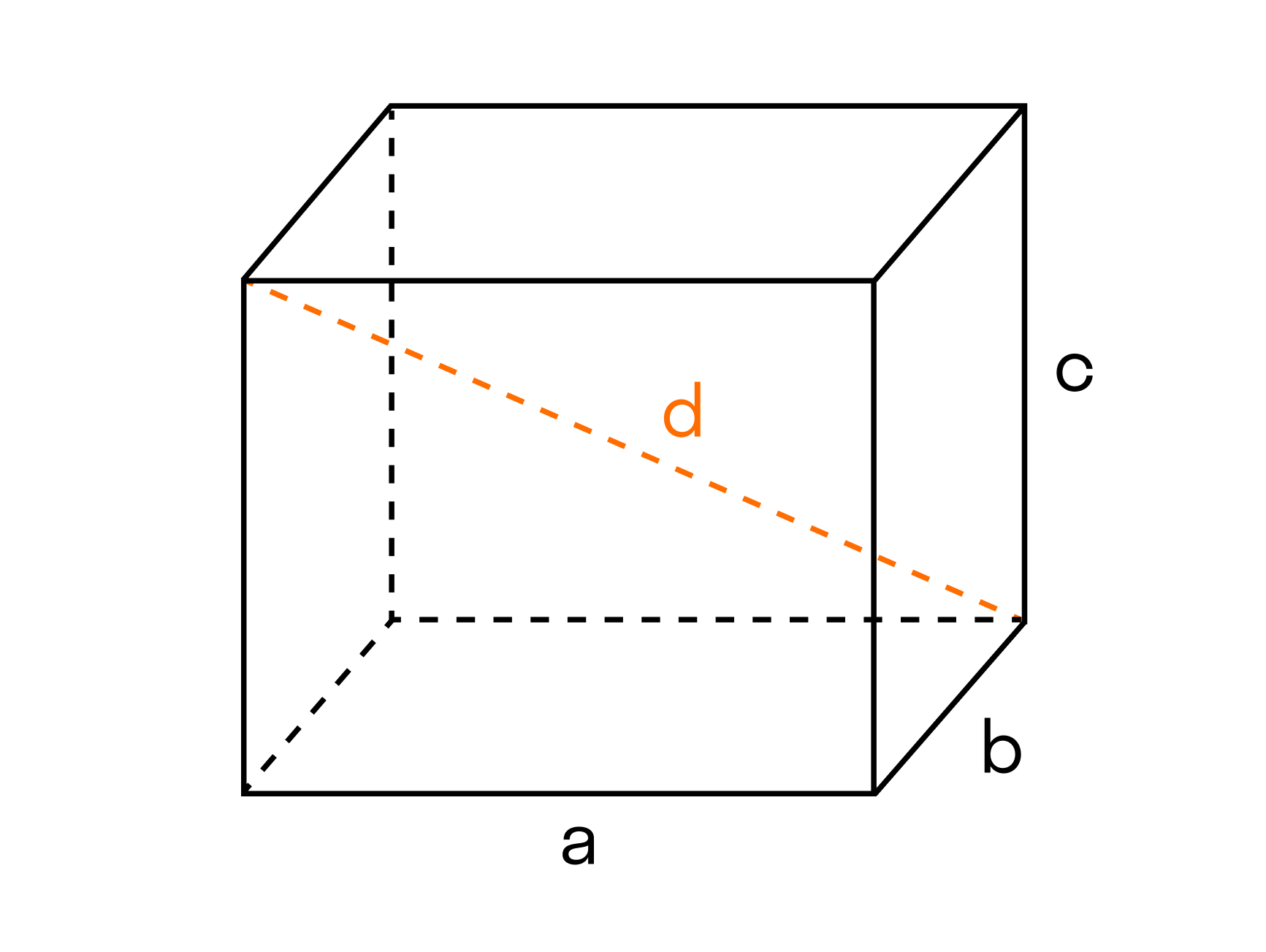
Например, чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.

А для цилиндра будет справедлива такая формула:

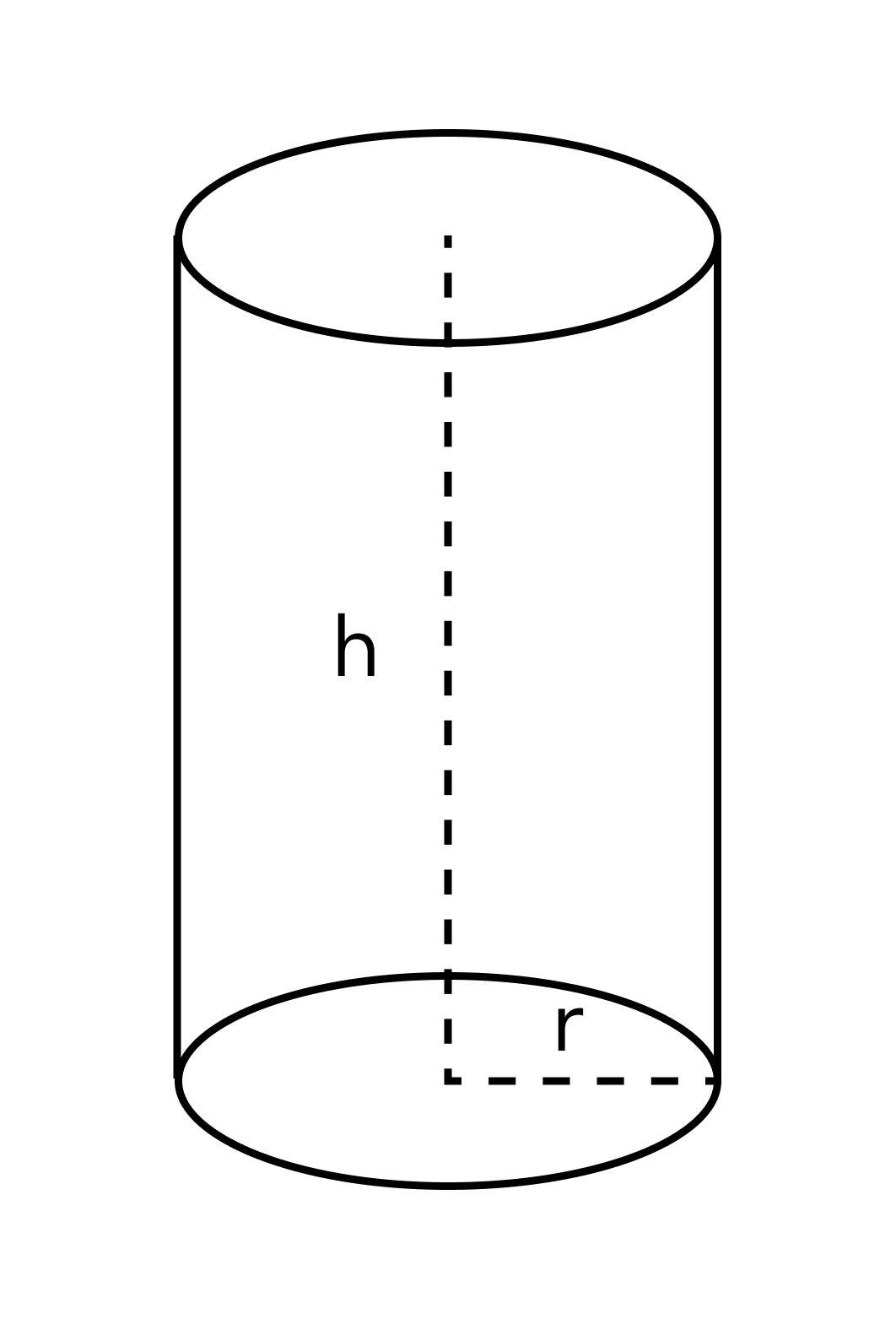
Плотность вещества

Плотность — скалярная физическая величина. Определяется как отношение массы тела к занимаемому этим телом объёму.

Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.

Маленькое исключение Исключение составляет вода. Так, плотность воды меньше плотности льда. Объяснение кроется в молекулярной структуре льда. Когда вода переходит из жидкого состояния в твердое, она изменяет молекулярную структуру так, что расстояние между молекулами увеличивается. Соответственно, плотность льда меньше плотности воды.

Ниже представлены значения плотностей для разных веществ. В дальнейшем это поможет при решении задач.

Где самая большая плотность? Самая большая плотность во Вселенной — в черной дыре. Плотность черной дыры составляет около 1014 кг/м3

Средняя плотность

В школьном курсе чаще всего говорят о средней плотности тела. Дело в том, что если мы рассмотрим какое-нибудь неоднородное тело, то в одной его части будет, например, большая плотность, а в другой — меньшая.

Если вы когда-то делали ремонт, то знакомы с такой вещью, как цемент. Он состоит из двух веществ: клинкера и гипса. Значит нам нужно отдельно найти плотность гипса, плотность клинкера по формуле, указанной выше, а потом найти среднее арифметическое двух плотностей. Можно сделать так.

А можно просто массу цемента разделить на объем цемента и мы получим ровно то же самое. Просто в данном случае мы берем не массу и объем вещества, а массу и объем тела.

Решение задач: плотность вещества

А теперь давайте тренироваться!

Задача 1

Цилиндр 1 поочерёдно взвешивают с цилиндром 2 такого же объёма, а затем с цилиндром 3, объем которого меньше (как показано на рисунке).

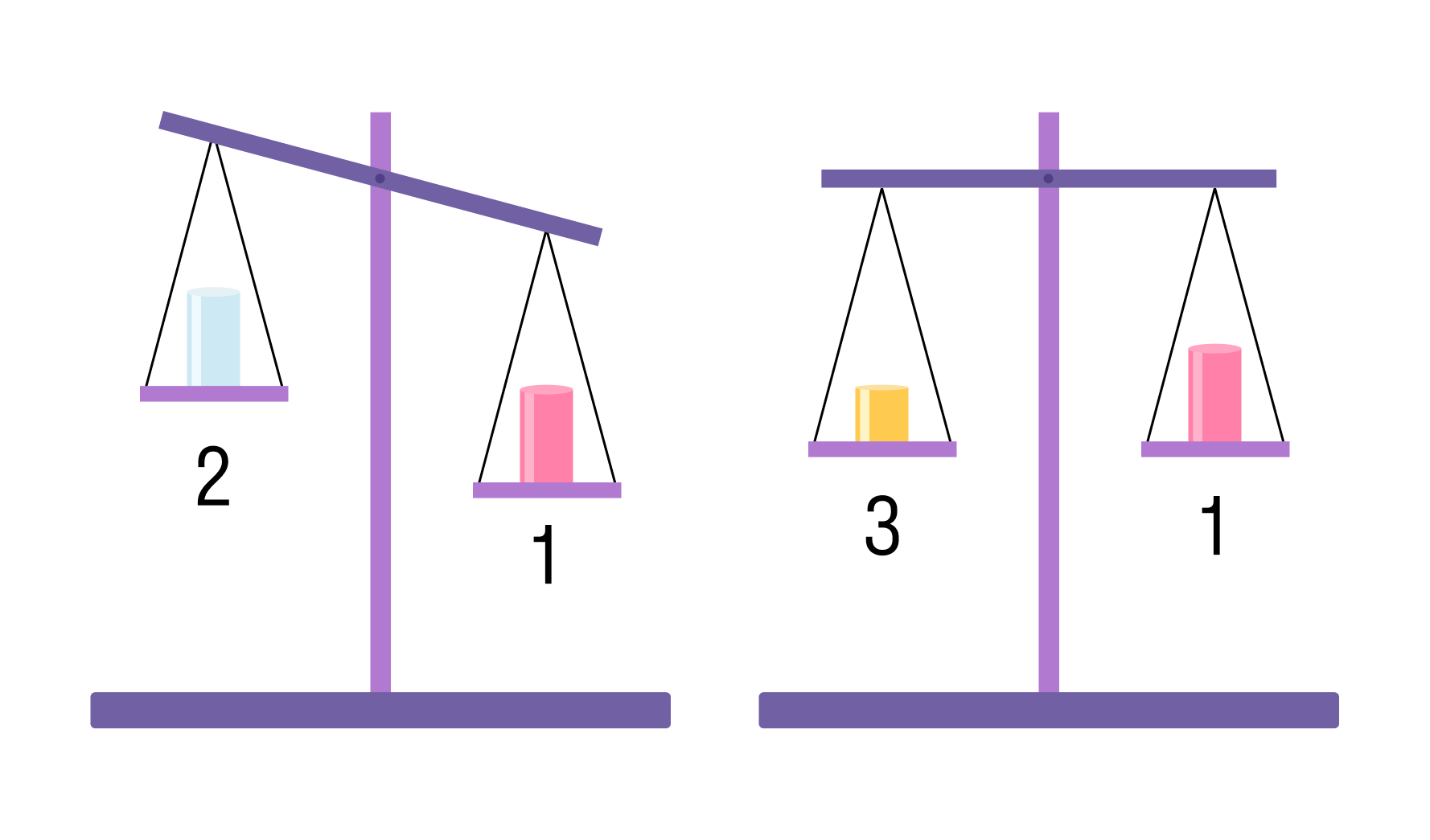
Какой цилиндр имеет максимальную среднюю плотность?

Решение:

Плотность тел прямо пропорциональна массе и обратно пропорциональна объему:

р = m/V

Исходя из проведенных опытов можно сделать следующие выводы:

1) масса первого цилиндра больше массы второго цилиндра при одинаковом объеме. Значит плотность первого цилиндра выше плотности второго.

2) масса первого цилиндра равна массе третьего цилиндра, объем которого меньше. Следовательно, плотность третьего цилиндра больше плотности первого цилиндра.

Таким образом, средние плотности цилиндров:

р2 &lt, р1 &lt, р3

Ответ: 3.

Задача 2

Шар 1 последовательно взвешивают на рычажных весах с шаром 2 и шаром 3 (как показано на рисунке). Для объёмов шаров справедливо соотношение V1 = V3 &lt, V2.

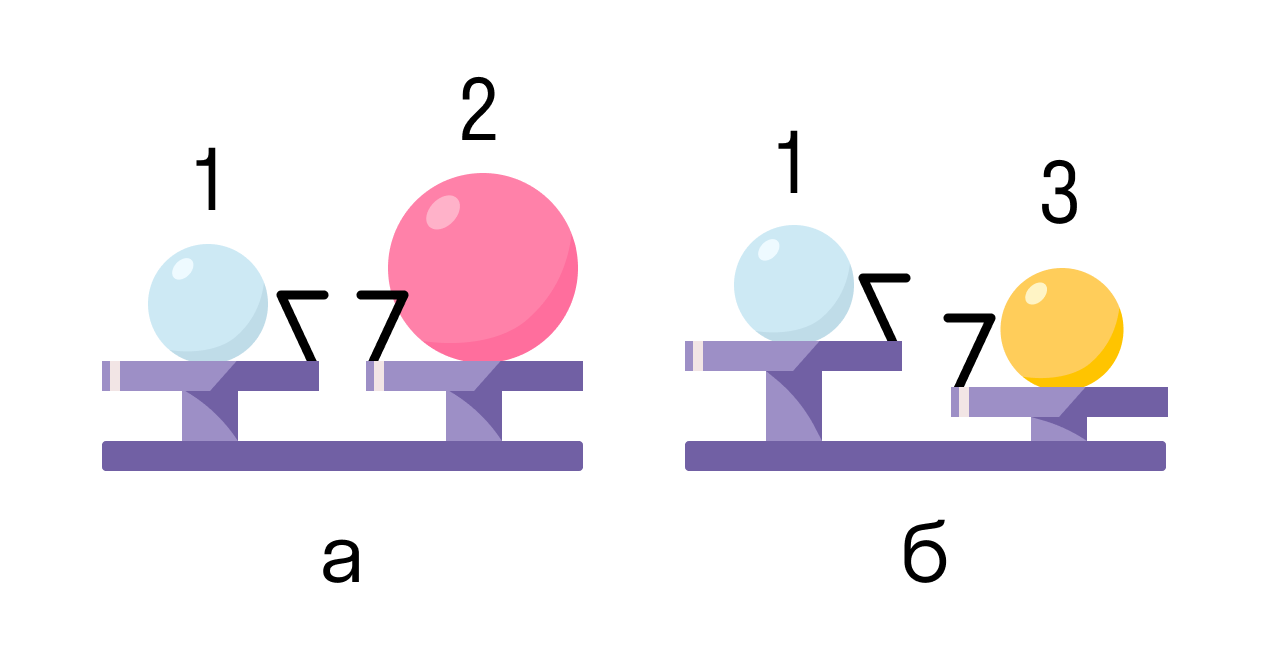
Какой шар имеет максимальную среднюю плотность?

Решение:

Из рисунка ясно, что масса шаров 1 и 2 равна — следовательно, плотность второго шара меньше, чем первого. Третий шар тяжелее, чем первый при одинаковом объёме, поэтому плотность третьего шара больше плотности первого. Таким образом, максимальную среднюю плотность имеет шар 3.

Ответ: 3

Задача 3

Найти плотность шара объемом 0,5 м^3 и массой 1,5 кг.

Решение:

Возьмем формулу плотности и подставим в нее данные нам значения.

р = m/V

р = 1,5/0,5 = 3 кг/м^3

Ответ: р = 3 кг/м^3

Плавание тел

Почему шарик с гелием взлетает? Или мяч при игре в водное поло не тонет? Жидкости и газы действуют на погруженные тела с выталкивающей силой. Подробно это явление рассматривают в теме «‎Сила Архимеда»‎. Если говорить простым языком: если плотность тела, погруженного в воду, больше плотности воды — тело пойдет ко дну. Если меньше – оно всплывет на поверхность.

Задача 1

Стальной шарик в воде падает медленнее, чем в воздухе. Чем это объясняется?

Решение:

Плотность воды значительно выше, чем воздуха, поэтому стальной шарик в воде падает медленнее

Задача 2

В таблице даны плотности некоторых твердых веществ. Если вырезать из этих веществ кубики, то какие кубики смогут плавать в воде? Плотность воды — 1000 кг/м3.

Решение:

Плавать будут кубики, плотность которых меньше плотности воды, то есть сделанные из парафина или сосны.

Плотность – полезная характеристика. У каждого материала есть характерная плотность, и все они не совпадают, поэтому вы можете использовать плотность в качестве метода идентификации. Так Архимеду удалось определить, была ли корона, подаренная ему царем, золотой или нет.

Плотность определяется как масса на единицу объема, что означает, что если вы хотите рассчитать плотность чего-либо, вы должны измерить его массу, а затем рассчитать его объем. Формула плотности:

rho = frac {m} {V}

гдеρэто плотность,мэто масса иVобъем материала.

Для обычных фигур, таких как кубы, прямоугольные коробки и пирамиды, легко вычислить объем, потому что все, что вам нужно сделать, это измерить размеры и использовать формулу. То же верно и для сфер.

Как рассчитать объем сферы

Формула объема сферы 4/3 × πр​³, гдер– радиус сферы. Это довольно просто, но на практике бывает сложно измерить радиус. Даже если у вас есть масштабированная 2D-проекция сферы, с которой можно работать, все равно будет сложно определить центр.

Обычно легче измерить диаметр, который равен удвоенному радиусу. Это означаетр​ = ​d/ 2, поэтому после выполнения арифметики вы можете переписать формулу объема в терминах диаметра следующим образом:

V = frac {1} {6} × πd ^ 3

Масса сферы vs. Масса

Всегда есть небольшая путаница между массой и весом. Масса, которая является величиной, необходимой для определения плотности, представляет собой внутреннее инерционное сопротивление тела изменению движения, но вес – это сила, действующая на тело под действием силы тяжести. Масса может быть измерена в килограммах, но вес измеряется в ньютонах. В имперской системе единица измерения массы – пули, а вес измеряется в фунтах.

Согласно принятому соглашению объекты взвешиваются в килограммах в системе СИ, которая является единицей массы, и в фунтах в британской системе мер, которые представляют собой единицы веса. При проведении измерений на поверхности Земли эти различия обычно безопасно игнорировать, но не в космосе, где сила тяжести другая.

Расчет плотности сферы

После того, как вы взвесите сферу, о которой идет речь, вы получите значением. Теперь все, что вам нужно сделать, это вычислить его объем (V), что можно сделать, измерив его диаметр,d. Формула плотности:ρ​ = ​м​/​V, и вы можете изменить эту формулу объема, чтобы выразить отношения в терминахd​:

begin {align} rho & = frac {m} {(1/6) × πd ^ 3} \ & = frac {6m} {πd ^ 3} end {выравнивается}

Использование плотности для вычисления массы или объема сферы

Предположим, у вас есть пушечное ядро, полностью сделанное из железа. Вы можете посмотреть плотность железа в таблице: 7,8 г / см³. Вы взвешиваете пушечное ядро ​​и обнаруживаете, что оно весит 20 фунтов. Теперь у вас есть достаточно информации, чтобы рассчитать его объем, поэтому просто измените формулу плотности, чтобы найти V:V​ = ​м​/​ρ​.

Есть только одна проблема. Плотность указывается в метрических единицах CGS, а вес – в британских единицах. В зависимости от того, какой объем вам нужен – в метрических или британских единицах, вы можете либо преобразовать вес в килограммы, либо найти плотность в фунтах на кубический дюйм. Используйте любое из этих преобразований:

1 ; text {lb} = 0,45359 ; text {кг, поэтому} 20 ; text {lbs} = 9,07 ; text {кг} \ 7,8 ; text {г / см} ^ 3 = 0,28 ; text {фунт / дюйм} ^ 3

Как вариант, вы можете рассчитать вес (массу) пушечного ядра, если сможете измерить его диаметр. Используйте эту формулу:

m = frac {1} {6} rhoπd ^ 3