| Плотность | |
|---|---|
 |
|
| Размерность | L−3 M |
| Единицы измерения | |
| СИ | кг/м³ |
| СГС | г/см³ |
| Примечания | |
| скалярная величина |
Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или как производная массы по объёму:
.
Данные выражения не эквивалентны, и выбор зависит от того, какая именно плотность рассматривается. Различаются:
Для точечной массы плотность является бесконечной. Математически её можно определить или как меру, или как производную Радона — Никодима по отношению к некоторой опорной мере.
Для обозначения плотности обычно используется греческая буква 
Понятие «плотность» в физике может иметь более широкую трактовку. Существуют поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам. Кроме того, говорят не только о плотности массы, но и о плотности других величин, например энергии, электрического заряда. В таких случаях к термину «плотность» добавляются конкретизирующие слова, скажем «линейная плотность заряда». «По умолчанию» под плотностью понимается вышеуказанная (трёхмерная, кг/м³) плотность массы.
Формула нахождения плотности[править | править код]
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где M — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.
При вычислении плотности газов при стандартных условиях эта формула может быть записана и в виде:
где 

Плотность тела в точке записывается как
тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как
Случай сыпучих и пористых тел[править | править код]
В случае сыпучих и пористых тел различают
- истинную плотность, определяемую без учёта пустот;
- насыпную плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.
Истинную плотность из насыпной (кажущейся) получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.
Зависимость плотности от температуры[править | править код]
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.
Диапазон плотностей в природе[править | править код]
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда (2·10−31—5·10−31 кг/м³, без учёта тёмной материи)[2].
- Плотность межзвёздной среды приблизительно равна 10−23—10−21 кг/м³.
- Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
- Плотность газообразного водорода (самого лёгкого газа) при стандартных условиях равна 0,0899 кг/м³.
- Плотность сухого воздуха при стандартных условиях составляет 1,293 кг/м³.
- Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
- Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
- Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
- Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
- Плотность пресной воды при 4 °C 1000 кг/м³.
- Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
- Гранит имеет плотность 2600 кг/м³.
- Средняя плотность Земли равна 5520 кг/м³.
- Плотность железа равна 7874 кг/м³.
- Плотность металлического урана 19100 кг/м³.
- Плотность золота 19320 кг/м³.
- Плотность нептуния — самого плотного актиноида — 20200 кг/м³.
- Самые плотные вещества при стандартных условиях — металлы платиновой группы шестого периода (осмий, иридий, платина), а также рений. Имеют плотность 21000—22700 кг/м³.
- Плотность атомных ядер приблизительно 2·1017 кг/м³.
- Теоретически верхняя граница плотности по современным[когда?] физическим представлениям — это планковская плотность 5,1⋅1096 кг/м³.
Плотности астрономических объектов[править | править код]
Средняя плотность небесных тел Солнечной
системы (в г/см³)[3][4][5]
- Средние плотности небесных тел Солнечной системы см. на врезке.
- Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.
- Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
- Плотность межгалактической среды 2×10−34÷5×10−34 кг/м³.
- Средняя плотность красных гигантов на много порядков меньше чем у Солнца из-за того, что их радиус в сотни раз больше.
- Плотность белых карликов 108÷1012 кг/м³
- Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
- Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:
- Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M−2). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 1019 кг/м³, превышающей ядерную плотность (2×1017 кг/м³), то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).
Плотности некоторых газов[править | править код]
| Азот | 1,250 | Кислород | 1,429 |
| Аммиак | 0,771 | Криптон | 3,743 |
| Аргон | 1,784 | Ксенон | 5,851 |
| Водород | 0,090 | Метан | 0,717 |
| Водяной пар (100 °C) | 0,598 | Неон | 0,900 |
| Воздух | 1,293 | Радон | 9,81 |
| Гексафторид вольфрама | 12,9 | Углекислый газ | 1,977 |
| Гелий | 0,178 | Хлор | 3,164 |
| Дициан | 2,38 | Этилен | 1,260 |
Для вычисления плотности произвольного идеального газа, находящегося в произвольных условиях, можно использовать формулу, выводящуюся из уравнения состояния идеального газа:[6]
,
где:
Плотности некоторых жидкостей[править | править код]
| Бензин | 710 | Молоко | 1040 |
| Вода (4 °C) | 1000 | Ртуть (0 °C) | 13600 |
| Керосин | 820 | Диэтиловый эфир | 714 |
| Глицерин | 1260 | Этанол | 789 |
| Морская вода | 1030 | Скипидар | 860 |
| Масло оливковое | 920 | Ацетон | 792 |
| Масло моторное | 910 | Серная кислота | 1835 |
| Нефть | 550—1050 | Жидкий водород (−253 °C) | 70 |
Плотность некоторых пород древесины[править | править код]
| Бальса | 0,15 | Пихта сибирская | 0,39 |
| Секвойя вечнозелёная | 0,41 | Ель | 0,45 |
| Ива | 0,46 | Ольха | 0,49 |
| Осина | 0,51 | Сосна | 0,52 |
| Липа | 0,53 | Конский каштан | 0,56 |
| Каштан съедобный | 0,59 | Кипарис | 0,60 |
| Черёмуха | 0,61 | Лещина | 0,63 |
| Грецкий орех | 0,64 | Берёза | 0,65 |
| Вишня | 0,66 | Вяз гладкий | 0,66 |
| Лиственница | 0,66 | Клён полевой | 0,67 |
| Тиковое дерево | 0,67 | Бук | 0,68 |
| Груша | 0,69 | Дуб | 0,69 |
| Свитения (Махагони) | 0,70 | Платан | 0,70 |
| Жостер (крушина) | 0,71 | Тис | 0,75 |
| Ясень | 0,75 | Слива | 0,80 |
| Сирень | 0,80 | Боярышник | 0,80 |
| Пекан (кария) | 0,83 | Сандаловое дерево | 0,90 |
| Самшит | 0,96 | Эбеновое дерево | 1,08 |
| Квебрахо | 1,21 | Бакаут | 1,28 |
| Пробка | 0,20 |
Плотность некоторых металлов[править | править код]
Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.
| Осмий | 22610[7] | Родий | 12410[8] | Хром | 7190[9] |
| Иридий | 22560[10] | Палладий | 12020[11] | Германий | 5320[12] |
| Плутоний | 19840[13] | Свинец | 11350[14] | Алюминий | 2700[15] |
| Платина | 19590[16] | Серебро | 10500[17] | Бериллий | 1850[18] |
| Золото | 19300[14] | Никель | 8910[19] | Рубидий | 1530[20] |
| Уран | 19050[21] | Кобальт | 8860[22] | Натрий | 970[23] |
| Тантал | 16650[24] | Медь | 8940[25] | Цезий | 1840[26] |
| Ртуть | 13530[27] | Железо | 7870[28] | Калий | 860[29] |
| Рутений | 12450[30] | Марганец | 7440[31] | Литий | 530[32] |
Измерение плотности[править | править код]
Для измерений плотности используются:
- Пикнометр — прибор для измерения истинной плотности
- Различные виды ареометров — измерители плотности жидкостей.
- Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
- Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
- Метод гидростатического взвешивания.
Остеоденситометрия — процедура измерения плотности костной ткани человека.
См. также[править | править код]
Видеоурок: плотность вещества
- Список химических элементов с указанием их плотности
- Удельный вес
- Удельная плотность
- Относительная плотность
- Объёмная плотность
- Конденсация
- Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
- Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
- Концентрация частиц
- Концентрация растворов
- Плотность заряда
- Уравнение неразрывности
Примечания[править | править код]
- ↑ Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
- ↑ Агекян Т. А. . Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
- ↑ Planetary Fact Sheet Архивировано 14 марта 2016 года. (англ.)
- ↑ Sun Fact Sheet Архивная копия от 15 июля 2010 на Wayback Machine (англ.)
- ↑ Stern, S. A., et al. The Pluto system: Initial results from its exploration by New Horizons (англ.) // Science : journal. — 2015. — Vol. 350, no. 6258. — P. 249—352. — doi:10.1126/science.aad1815.
- ↑ МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА. Учебно-методическое пособие к лабораторным работам № 1-51, 1-61, 1-71, 1-72. Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров (2014). Дата обращения: 4 января 2019. Архивировано 23 ноября 2018 года.
- ↑ Krebs, 2006, p. 158.
- ↑ Krebs, 2006, p. 136.
- ↑ Krebs, 2006, p. 96.
- ↑ Krebs, 2006, p. 160.
- ↑ Krebs, 2006, p. 138.
- ↑ Krebs, 2006, p. 198.
- ↑ Krebs, 2006, p. 319.
- ↑ 1 2 Krebs, 2006, p. 165.
- ↑ Krebs, 2006, p. 179.
- ↑ Krebs, 2006, p. 163.
- ↑ Krebs, 2006, p. 141.
- ↑ Krebs, 2006, p. 67.
- ↑ Krebs, 2006, p. 108.
- ↑ Krebs, 2006, p. 57.
- ↑ Krebs, 2006, p. 313.
- ↑ Krebs, 2006, p. 105.
- ↑ Krebs, 2006, p. 50.
- ↑ Krebs, 2006, p. 151.
- ↑ Krebs, 2006, p. 111.
- ↑ Krebs, 2006, p. 60.
- ↑ Krebs, 2006, p. 168.
- ↑ Krebs, 2006, p. 101.
- ↑ Krebs, 2006, p. 54.
- ↑ Krebs, 2006, p. 134.
- ↑ Krebs, 2006, p. 98.
- ↑ Krebs, 2006, p. 47.
Литература[править | править код]
- Плотность — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
- Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
- Krebs R. E. . The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.
Ссылки[править | править код]
- Онлайн интерактивная таблица плотности веществ Архивная копия от 29 апреля 2011 на Wayback Machine (рус.)
- Подробная таблица значений плотности распространенных жидкостей Архивная копия от 5 октября 2016 на Wayback Machine (рус.)
- Урок по теме “Плотность вещества” Архивная копия от 30 января 2022 на Wayback Machine
Загрузить PDF
Загрузить PDF
Плотность тела является отношением массы к объему. Значение плотности может использоваться в геологии, физике и других естественных науках. Также от этого свойства зависит плавучесть или способность тела держаться на поверхности воды, в которой используется единица плотности в 1 грамм на кубический сантиметр (г/см3) — стандартные единицы измерения плотности.
-
1
Измерьте массу оборудования перед началом работы. Если вам требуется рассчитать плотность жидкости и в особенности газа, то нужно знать массу емкости. Это позволит вам вычесть массу из общей массы при измерении массы тела или вещества.[1]
- Поместите пустую пробирку, сосуд или другую емкость на весы и запишите массу в граммах.
- Некоторые весы позволяют «тарировать» вес. В этом случае поместите емкость на весы, после чего нажмите кнопку «Тарировать», чтобы на весах обнулилось значение массы. Такая функция позволяет вычесть массу емкости, в которой находится вещество.
-
2
Поместите тело на весы и узнайте массу. Поместите твердое тело либо емкость с жидкостью или газом на весы, чтобы измерить массу. Запишите массу в граммах без учета массы использованной емкости.[2]
-
3
Переведите массу в граммы, если используются другие единицы. Некоторые весы могут работать с другими единицами. Если в весах не используются граммы, потребуется преобразовать единицы путем умножения на коэффициент пересчета.
- 1 унция — это примерно 28,35 граммов. 1 фунт — примерно 453,59 граммов.
- В этих случаях нужно умножить массу тела на коэффициент пересчета 28,35 для унций и 453,59 для перевода фунтов в граммы.
-
4
Узнайте объем тела в кубических сантиметрах. Если вам повезло и тело имеет прямоугольные грани, то достаточно изменить длину, ширину и высоту тела в сантиметрах. Перемножьте все три значения между собой, чтобы получить объем.[3]
-
5
Определите объем тела другой формы. Для жидкости и газа нужно использовать градуированный цилиндр или пробирку, чтобы узнать объем. Для твердых тел неправильной формы потребуется использовать соответствующую формулу или погрузить данное тело в воду, чтобы подсчитать объем.
- 1 миллилитр равен 1 кубическому сантиметру. Преобразовать объем воды и газа очень просто!
- Существуют различные математические формулы для расчета объема прямоугольной призмы , цилиндра, пирамиды и других тел.
- Твердое и плотное тело неправильной формы вроде камня с неровными сторонами требуется погрузить в воду и узнать объем вытесненной воды. Согласно закону Архимеда, тело вытесняет объем жидкости, равный собственному объему. Далее следует вычесть объем жидкости из общего объема жидкости с погруженным в нее телом.[4]
Реклама
-
1
Разделите массу тела на объем. Разделите массу вещества в граммах на значение объема в кубических сантиметрах с помощью калькулятора или в столбик (возможно даже в уме). Для тела массой 20 граммов, которое занимает объем в 5 кубических сантиметров, значение плотности составит 4 грамма на кубический сантиметр.[5]
-
2
Упростите ответ до подходящего значения в значащих цифрах. В реальном мире обычно используются не настолько точные значения, как в задачах. Следовательно, если вы разделите реальную массу на объем, то получите длинное число с большим количеством знаков после запятой.
- Уточните значащие цифры у преподавателя или человека, которому требуются ваши расчеты.
- Обычно следует округлять до 2–3 знаков после десятичного разделителя. Следовательно, ваш результат вроде 32,714907 можно округлить до 32,71 или 32,715 г/см3.
-
3
Практическое применение. Обычно значение плотности тела соотносится с плотностью воды (1,0 г/см3). Тело тонет в воде, если его плотность выше единицы. В других случаях тело будет плавучим.
- Это же касается некоторых жидкостей. Например, если попытаться смешать оливковое масло с водой, то масло всплывет на поверхность по причине меньшей плотности.
- Также плотность соотносится с удельной плотностью. Часто она представляет собой плотность тела, разделенную на плотность воды (или другого вещества). Единицы измерения сокращаются, в результате чего остается число, которое представляет собой удельный вес. Его часто используют в химии, чтобы определить концентрацию вещества в растворе.[6]
Реклама
Что вам понадобится
- Обычные или пружинные весы
- Рулетка или измерительная лента
- Калькулятор
- Градуированный цилиндр (для порошков, жидкостей или газов)
Об этой статье
Эту страницу просматривали 34 464 раза.
Была ли эта статья полезной?
Онлайн-калькулятор плотности, который поможет вам определить соотношение между плотностью, массой и весом объекта с помощью формулы плотности. В этом калькуляторе есть небольшая, но очень важная опция, где вы можете легко определить плотность объекта по категории и названию материала. Если вы хотите получить краткие сведения о том, как рассчитать плотность по формуле, продолжайте читать!
Кроме того, вы можете попробовать наш онлайн-калькулятор импульса, который поможет вам найти импульс движущегося объекта, а также определить массу объекта.
Читать дальше!
Что такое формула плотности?
Расчеты не слишком сложные, а очень простые. Просто введите значения в следующее уравнение плотности, чтобы легко вычислить любую из требуемых переменных:
р = м / В
Где,
V – объем & m – масса объекта.
Если вы хотите найти объем с помощью плотности и массы, калькулятор плотности использует формулу:
V = м / п
Чтобы найти массу с плотностью и объемом, рассмотрите следующую формулу:
т = р * V
Плотность можно определить как массу на единицу объема объекта. Со значениями введите единицы измерения, и этот калькулятор выполнит преобразование единиц измерения.
Как найти плотность объекта по массе и объему (шаг за шагом):
Рассчитать плотность с помощью этого расчет плотности очень просто. Вы можете найти любое из трех значений, введя два значения в формулу. Вот пример для каждого расчета:
Проведите по!
Пример:
Объект весил около 150 г и объем 90 см3. Найти плотность объекта?
Решение:
Формула:
р = м / В
Вот,
m = 150 г
V = 90 см3
Так,
р = 150/90
p = 1,66 г · см-3
как определить плотность объем по и массе:
Вы можете легко определить объем объекта, изменив уравнение плотности. Давайте посмотрим на пример:
Пример:
Какой у тела объем, если его масса 500 г, а плотность 4 см-3?
Решение:
Формула:
V = м / п
Вот,
м = 500г
р = 4 см-3
Так,
V = 500/4
V = 125 см3
Как найти массу объекта с учетом плотности и объема:
Расчет массы по объему и плотности становится простым. Просто следуйте следующему примеру:
Пример:
Объем объекта 200 см3, а плотность 9 см-3, какова масса объекта?
Решение:
Формула:
т = р * V
Вот,
V = 200 см3
р = 9 см-3
Так,
т = (9) * (200)
м = 1800г
Какая плотность воды?
Плотность воды между 0 ° C и 4 ° C обычно составляет 100 кг / м3, но она меняется в зависимости от температуры. При повышении температуры объем материала увеличивается. Согласно формуле, объем и плотность обратно пропорциональны друг другу, в конечном итоге плотность материала уменьшается. Плотность воды при различных температурах приведена в следующей таблице:
Стол
Ниже приведена таблица единиц, в которой плотность обычно выражается плотностями некоторых материалов.
Столы
Как пользоваться калькулятором плотности:
Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!
Входы:
- Прежде всего, выберите во вкладке то, что вам нужно найти.
- Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
- Наконец, нажмите кнопку “Рассчитать”.
Выходы:
Как только вы заполните все поля, калькулятор покажет:
- Плотность объекта
- Масса объекта
- Объем объекта
- Корень кубический из объема
Заметка:
Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.
Заключение:
Плотности широко используются для идентификации чистых веществ и определения состава различных видов смесей. В реальной жизни это полезно, когда выясняется, что что-то будет плавать в воде, и важно при расчете объема и массы вещества. Когда дело доходит до расчетов, запишите онлайн-калькулятор плотности, который поможет вам в кратчайшие сроки найти взаимосвязь между массой, объемом и плотностью вещества.
Others Languages:Density Calculator, Yoğunluk Hesaplama, Kalkulator Gęstości, Kalkulator Kepadatan, Dichte Rechner, 密度 計算, 밀도 계산, Výpočet Hustoty, Cálculo De Densidade, Calcul Densité, Calculadora De Densidad, Calcolo Densità, حساب الكثافة, Tiheys Laskuri, Massefylde Beregning, Tetthets Kalkulator.
Содержание:
- Определение и формула плотности вещества
- Виды плотности вещества
- Единицы измерения плотности вещества
- Примеры решения задач
Определение и формула плотности вещества
Определение
Плотностью вещества (плотностью вещества тела) называют скалярную физическую величину, которая равна отношению массы
(dm) малого элемента тела к его единичному объему (dV). Чаще всего плотность вещества обозначают греческой буквой
$rho$. И так:
$$rho=frac{d m}{d V}$$
Виды плотности вещества
Применяя выражение (1) для определения плотности, говорят о плотности тела в точке.
Плотность тела зависит от материала тела и его термодинамического состояния.
В том случае, если тело можно считать однородным (плотность вещества во всем теле одинакова (
$rho = const$), то $rho$ определяют следующей формулой:
$$rho=frac{m}{V}$$
где m – масса тела, V – объем тела.
Если тело является неоднородным, то иногда пользуются понятием средней плотности
$langlerhorangle$, которая рассчитывается как:
$$langlerhorangle=frac{m}{V}(3)$$
где m – масса тела, V – объем тела. В технике для неоднородных (например, сыпучих) тел используют понятие объемной плотности.
Объемную плотность рассчитывают так же как $langlerhorangle=frac{m}{V}(3)$ (3). Объем определяют,
включая промежутки в сыпучих и рыхлых материалах (таких как: песок, гравий, зерно и т.д.).
При рассмотрении газов, находящихся в нормальных условиях для вычисления плотности применяют формулу:
$$rho=frac{mu}{V_{mu}}(4)$$
где $mu$ – молярная масса газа,
$V_{mu}$ – молярный объем газа, который при нормальных условиях составляет 22,4 л/моль.
Единицы измерения плотности вещества
В соответствии с определением, можно записать, что
единицами измерения плотности в системе СИ служит: [$rho$]=кг/м3
в СГС: [$rho$]=г/(см)3
При этом: 1 кг/м3 = (10)-3 г/(см)3 .
Примеры решения задач
Пример
Задание. Какова плотность воды, если объем, который занимает одна молекула H2O,
примерно равен $Delta V approx 3 cdot 10^{-29}$ м3? Считайте, что молекулы в воде плотно упакованы.
Решение. Если считать, что молекулы в воде плотно упакованы, то ее плотность можно найти как:
$$rho=frac{m_{0}}{Delta V}$$
где m0 – масса молекулы воды. Найдем m0, используя известное соотношение:
$$frac{m}{mu}=frac{N}{N_{A}}$$
где N=1 – количество молекул (в нашем случае одна молекула), m – масса рассматриваемого количества молекул
(в нашем случае m=m0), NА=6,02• 1023 моль-1 – постоянная Авогадро,
$mu$=18•10-3
кг/моль (так как относительная молекулярная масса воды равна Mr=18). Следовательно, применяя выражение (2)
для нахождения массы одной молекулы имеем:
$$m_{0}=frac{mu}{N_{A}}(3)$$
Подставим m0 в выражение (1), получаем:
$$rho=frac{mu}{Delta V N_{A}}(4)$$
Проведем расчет искомой величины:
$rho=frac{18 cdot 10^{-3}}{3 cdot 10^{-29} cdot 6,02 cdot 10^{23}}=10^{3} mathrm{kr} / mathrm{m}^{3}$ кг/м3
Ответ. Плотность воды равна 103 кг/м3 .

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
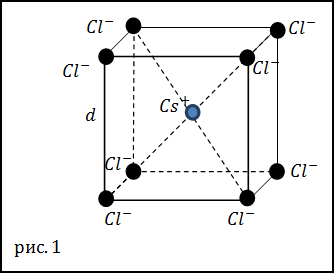
Задание. Какова плотность кристаллов хлорида цезия (CsCl), если кристаллы имеют кубическую кристаллическую
решетку (рис.1) в вершинах которой находятся ионы хлора (Cl–), а в центре расположен ион цезия
(Cs+). Ребро кристаллической решетки считайте равным d=0, 41 нм.
Решение. За основу решения задачи примем выражение:
$$frac{m}{mu}=frac{N}{N_{A}}(2.1)$$
где m – масса вещества (в нашем случае это масса одной молекулы
$left.operatorname{CsCl}left(m_{0}right)right), N=1, N_{A}=6,02 cdot 10^{23}$ – постоянная Авогадро,
$mu=168 cdot 10^{-3}$ кг/моль молярная масса хлорида Цезия
(так как относительная молекулярная хлорида цезия равна $M_r = 168$).
Выражение (2.1) для одной молекулы примет вид:
$$frac{m_{0}}{mu}=frac{1}{N_{A}}$$
В выражении (2.2) массу молекулы можно выразить через ее плотность как:
$$m_{0}=rho V_{m}(2.3)$$
где Vm – объем исследуемой молекулы. Так как кристаллы имеют кубическую кристаллическую решетку, ребро которой нам известно
(и равно d), то вместо объема Vm можно использовать выражение:
$$V_{m}=d^{3}(2.4)$$
Подставим выражения (2.3) и (2.4) в формулу (2.2), получим:
$$frac{rho V_{m}}{mu}=frac{1}{N_{A}}(2.5)$$
Тогда выражение для плотности примет вид:
$$rho=frac{mu}{d^{3} N_{A}}$$
Переведем размер стороны кристаллической решетки в единицы системы СИ, получим d=0,41нм=0, 41•10-9) м. Проведем вычисления:
$rho=frac{168 cdot 10^{-3}}{left(0,41 cdot 10^{-9}right)^{3} cdot 6,02 cdot 10^{23}}=4047,6$ кг/м3
Ответ. $rho=4047,6$ кг/м3
Читать дальше: Формула потенциальной энергии.
Найти массу, плотность или объем онлайн
На данной странице калькулятор поможет найти плотность, массу или объем вещества онлайн. Для расчета введите значения в калькулятор.
Объем, масса и плотность
Найти
Масса:
Объем:
Плотность:
Ответы:
Формула для нахождения массы тела через плотность и объем:
m – масса; V – объем; p – плотность.
Формула для нахождения объема тела через плотность и массу:
m – масса; V – объем; p – плотность.
Формула для нахождения плотности тела через объем и массу:
m – масса; V – объем; p – плотность.