Как найти плотность неоднородного тела

Как найти плотность неоднородного тела

Решение
задач на нахождение плотности смесей и сплавов,

средней
плотности неоднородных тел (7 класс)

Ларионов Вадим Сергеевич,

 учитель физики МБОУ Лицея №
15 г.Сарова, larionvadim@yandex.ru

Ларионова Наталья Валентиновна,

к.п.н., учитель физики МБОУ Лицея № 15
г.Сарова, nvlarionova@yandex.ru

В статье сформулированы методические рекомендации по
организации факультативного занятия по решению задач на нахождение плотности
смесей, сплавов и неоднородных тел. Представлены учебные материалы по теме,
структурированные по уровню сложности.

Задачи на
нахождение плотности смеси или сплава, средней плотности неоднородного
(«составного»)  тела являются базовыми при изучении темы «Плотность»  и
достаточно часто встречаются в олимпиадах по физике в 7-8-х классах. Именно
поэтому целесообразно данному типу задач посвятить отдельное факультативное занятие,
структура которого соответствует принципу «от простого к сложному» и содержит последовательные
блоки задач: ключевые, олимпиадные и задачи для самостоятельного решения (см.
приложение).

Средняя плотность
неоднородного («составного») тела, плотность смеси или сплава рассчитывается по
формуле

где m1, m2, m3… -массы отдельных частей тела
(компонентов смеси или сплава), а V1, V2, V3 … – их объёмы.

Для решения задач
по данной теме,  необходимо составить систему уравнений, в основе которой лежат
следующие положения:

1.       Определительная формула
плотности

2.       Свойство аддитивности массы
(масса смеси или сплава равна сумме масс его составных частей)

m=m1+ m2+ m3+…

3.       Как правило, в таких задачах
полагают, что объём сплава (смеси) равен сумме объёмов его составных частей

V=V1+V2+V3 …

В задачах, предложенных ниже,
исключением является задача № 6 из блока олимпиадных задач (задача о смешивании
спирта и воды).

Ключевые задачи,
представленные в занятии, в зависимости от подготовки учащихся могут быть
решены непосредственно на уроке при изучении темы «Плотность». В этом случае на
факультативном занятии рассматриваются олимпиадные задачи. Далее ученикам
предлагаются задачи для самостоятельного решения, которые, как правило,
составляют домашнее задание. В этом случае удобно дифференцировать домашнее
задание учеников, предложив не более трёх обязательных задач в зависимости от
уровня подготовленности учеников. Учитель может дополнить списки олимпиадных
задач и задач для самостоятельного решения, используя материалы последних
олимпиад.

Приложение

Плотность смесей, сплавов, «составных» тел

Цель:  Научиться решать задачи
на нахождение плотности смесей и сплавов, а также средней плотности
неоднородных тел («составных») тел.

Ключевые задачи

1.       Какова плотность сплава из
300г олова и 100г свинца? (8г/см3)

2.                    
Сплав
изготовлен из меди объёмом 0,4 м3  и цинка массой 710 кг. Какова
плотность сплава? (8540 кг/м3)

3.       Для приготовления вишнёвого
сиропа в кастрюлю вылили 1 л вишнёвого варенья и 2 л воды и хорошо перемешали.
Какова плотность сиропа, если плотность варенья 1300 кг/м3? (1100
кг/м3)

4.       Какова плотность смеси из
глицерина и спирта, если объём спирта составляет половину объёма смеси? Как
изменится ответ, если масса спирта составляет половину массы смеси? (1030 кг/м3, 980 кг/м3)

Олимпиадные задачи

1.       Масса первого изделия в 2
раза больше массы второго изделия, а их объёмы находятся в отношении V1:V2=1:3. Плотность первого изделия ρ1=4г/см3.
Какова будет средняя плотность «составного» тела, если два изделия склеить?
Массой и объёмом клея пренебречь. (1,5 г/см3)

2.       Изделие, склеенное из трёх
различных частей, имеет объём V=600см3.
Объёмы частей находятся в соотношении V1:V2:V3=2:3:5, а их плотности – в соотношении ρ1:ρ2:ρ3=4:3:1.
Чему равна масса изделия, если плотность первой части ρ1=2000кг/м3?
(660 г)

3.       Ученик измерил плотность
деревянного бруска, покрытого краской, и она оказалась равной ρ=600 кг/м3. Но на
самом деле брусок состоит из двух частей, равных по массе, плотность одной из
которых в два раза больше плотности другой. Найдите плотности обеих частей
бруска. Массой краски можно пренебречь. (450 кг/м3, 900 кг/м3)

4.       В дистиллированную воду
аккуратно вливают серную кислоту. Получившийся раствор имеет плотность ρр=1200
кг/м3 и массу m=120г. Объём раствора равен
сумме объёмов воды и кислоты. Плотность воды ρв=1000 кг/м3,
плотность кислоты ρк=1800 кг/м3.  Какова масса кислоты,
влитой в воду? (45 г)

5.       Однородный кубик со стороной
a и плотностью ρ поместили внутрь куска глины с плотностью 4ρ, которому придали
форму куба со стороной 2a. Получившийся куб облепили пластилином плотностью 2ρ,
в результате чего получился куб со стороной 3a (см. рисунок). Определите
среднюю плотность получившейся системы. (67ρ/27≈2,5ρ)

6.       Плотностью вещества называют
отношение массы тела из этого вещества к его объёму. Например, масса 1 см3
воды составляет 1 г, поэтому плотность воды 1 г/см3. Представим, что
смешали 100 литров воды и 100 литров спирта плотностью 0,8 г/см3, и
при смешении оказалось, что суммарный объём уменьшился на 5 процентов. Какова
плотность полученного раствора? (ρ=18/19 г/cм3≈0,95г/cм3)

Задачи
для самостоятельного решения

1.   Какую плотность имеет сплав
из 270г алюминия и 445г меди? (≈4,77
г/cм3)

2.   Сплав золота и серебра массой
400 г имеет плотность 1,4·104 кг/м3. Полагая объём сплава
равным сумме объёмов его составных частей, определите массу золота в сплаве? (220
г)

3.   Масса первого изделия в 3
раза меньше массы второго изделия, а их объёмы находятся в соотношении V1:V2=2:1. Плотность первого тела ρ1=1,8 г/см3.
Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой
и объёмом клея пренебречь. (4,8 г/см3)

4.   Изделие, склеенное из трёх
различных частей, имеет объём V=900см3.
Объёмы частей находятся в соотношении V1:V2:V3=5:3:1, а их плотности – в соотношении ρ1:ρ2:ρ3=1:2:5.
Чему равна масса изделия, если плотность первой части ρ1=500кг/м3?
(800 г)

5.       Кубик с ребром a=20см сделан из материала с
плотностью ρ=3000кг/м3. Однако внутри кубика имеется воздушная
полость, поэтому его средняя плотность ρср=1200кг/м3.
Определите объём этой воздушной полости. Во сколько раз изменится средняя
плотность кубика, если полость целиком заполнить водой? Массой воздуха внутри
полости можно пренебречь. (4800 см3, 1,5)

Литература к занятию

1.     Генденштейн Л.Э., Кирик Л.А.,
Гельгафт И.М. Задачи по физике с примерами решений. 7-9 классы. Под ред. В.А.Орлова.
– М.: Илекса, 2009. – 416 с.

2.       Бажанский И.И., Гой В.А.,
Чубов Ю.Б. Приморские олимпиады школьников по физике (2003-2007 гг). Учебное
пособие. – Владивосток: Изд-во Дальневост. ун-та, 2008. – 200с.

3.       Олимпиады 2008-2009. Физика.
Задачи Московских олимпиад школьников. Под ред. М.В.Семёнова, А.А.Якуты. – М.:
МЦНМО, 2009. – 70 с.

4.       400 физических этюдов.
Избранные задачи физических олимпиад Санкт-Петербурга. – СПб, 2006. –284 с.

5.       
Борисов
С.Н. Учебное пособие по физике для учащихся 7-го класса. – М.: МИФИ, 2009.  –
100 с.

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Скачиваний:

69

Добавлен:

31.03.2015

Размер:

1.78 Mб

Скачать

6.4. Измерительное устройство поляриметра

Прибор предназначен для определения концентрации растворов оптиче-

ски активных веществ. Определение концентрации сводится к определению уг-

ла поворота плоскости поляризации исследуемым раствором.

Рис. 5.8. Измерительная шкала поляриметра

На рис. 5.8 показана измерительная шкала поляриметра. Слева ос-

новная шкала (от 0 до 3600), справа неподвижная шкала нониуса.

На примере измерительной системы поляриметра произведем расчет це-

ны деления по формуле (5.1)

Для нониуса nн =25; Сш=0,5. Тогда Cн

nн 1

25 1

0,5 0,48

25

nн

Цена деления отсчета такого устройства (5.2)

С0=Сш – Сн=0,50-0,48=0,020

Задание к лабораторной работе

1.Измерьте с помощью штангенциркуля стороны бруска. Для каждой сто-

роны проведите не менее 8 измерений. Результаты измерений занесите в таблицу:

71

Экспериментальные и расчетные данные

n

hi

h

hi

(

h

hi )2

1

…..

8

2.Вычислить абсолютную и относительную погрешности прямых измере-

ний сторон.

3.Вычислить средний объем бруска.

4.Вычислить абсолютную и относительную погрешности косвенных изме-

рений объема бруска.

5.Запишите доверительный интервал измерений объема.

РАБОТА № 7. ИДЕНТИФИКАЦИЯ ВЕЩЕСТВ ПО ПЛОТНОСТИ С ПОМОЩЬЮ ПИКНОМЕТРА

Актуальность работы:

Денситометрия – физический метод анализа, основанный на определении плотности вещества. Плотность характеризует инерционные и гравитационные свойства вещества и является одной из важнейших физических констант. При исследовании лекарственных веществ по величине плотности можно иденти-

фицировать подлинность лекарственных препаратов.

Цель работы:

Изучить способ определения плотности твердого тела, нерастворимого в данной жидкости; освоить метод определения плотности пикнометром.

Целевые задачи:

знать: нахождение плотности однородного и неоднородного тела, зависи-

мость плотности от температуры.

72

уметь: определять плотность твёрдого тела, имеющего неправильные гео-

метрические формы (рассыпчатого) и нерастворимого в воде с помощью пикнометра, определять плотность неизвестной жидкости.

План подготовки конспекта:

1.Основные теоретические сведения

2.Выяснить, что измеряется в лабораторной работе, каким методом и для

чего.

2.Подготовить таблицы.

3.Записать расчётные формулы.

Вопросы для подготовки к входному тестированию:

1.Как найти плотность однородного и неоднородного тела?

2.Как зависит плотность от температуры?

3.В чём заключается метод определения плотности твёрдого тела,

имеющего неправильные геометрические формы (рассыпчатого) и нераствори-

мого в воде с помощью пикнометра?

4. В чём заключается метод определения плотности неизвестной жидко-

сти?

Теоретические сведения

Денситометрия – физический метод анализа, основанный на определении плотности вещества. Плотность характеризует инерционные и гравитационные свойства вещества и является одной из важнейших физических констант. При исследовании лекарственных веществ по величине плотности можно иденти-

фицировать подлинность лекарственных препаратов.

Плотностью однородного тела называется физическая величина, равная отношению массы тела m к его объёму V:

V

В СИ плотность измеряется в кг/м 3.

73

В неоднородных телах плотность различных его участков различна. По-

этому расчет плотности неоднородного вещества по указанной формуле не правомочен. Выберем в таком теле малый объём V, внутри которого тело можно считать практически однородным. Тогда средняя плотность выбранного

объёма будет равна m . Переходя к пределу, получим плотность тела в вы-

V

бранной точке:

lim

m

dm

.

V 0 V

dV

Для большинства веществ составлены таблицы плотности для температу-

ры 200С. При определении плотности различных веществ, с целью их иденти-

фикации, не обязательно доводить температуру до 200С. Плотность вещества определяют при температуре исследуемого объекта, а затем используют фор-

мулу объемного теплового расширения твердых и жидких тел, по которой объ-

ем тела V при температуре t 0 С, равен:

V=V0 (1 t0 ),

где V0 – начальный объём при температуре t0 0С; – коэффициент объем-

ного расширения, t 0 = t0 – t00 .

Следовательно, зависимость плотности от температуры можно записать в виде:

m

V0 0

0

, где –плотность при t0 .

V V0 (1 t)

1 t

0

0

7.2. Определение плотности твердого тела опытным путем

Приборы и принадлежности:

– пикнометр, аналитические весы, разновесы, термометр, пипетки, ис-

следуемые жидкость и твердое тело; – дистиллированная вода.

Рассмотрим методику определения плотности твердого тела, нераствори-

мого в данной жидкости, с помощью пикнометра. Пикнометр – стеклянная кол-

74

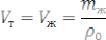
бочка с определенным объёмом (чаще это 25 мл или 50 мл), снабженная при-

тертой пробкой и имеющая метку на горлышке (см. рис. 6.1).

Чтобы определить плотность твердого тела, используя формулу (6.1), нужно знать массу исследуемого тела m и его объём V. Массу твердого тела можно определить взвешиванием на аналитических весах, но исследуемое тело может иметь неправильные геометрические размеры и определение его объёма путем измерений весьма проблематично. Поэтому объём тела определяют косвенным путем, основываясь на законе Архимеда, используя пикнометр. Объем тела равен объему вытесненной им жидкости, который можно найти по формуле:

где ρ0–плотность жидкости, mж– масса вытесненной твердым телом жид-

кости, равная

mж=Мпв+m-Mп

Объем тела определим расчетным путем: V

V

выт

Мпв m Мпв

.

Т

0

Тогда, подставляя в формулу (6.1) выражения для объема и массы твер-

дого тела получим расчетную формулу для плотности твердого тела:

0

m

Мпв m Мпв

7.3.Порядок выполнения работы

I. Определение плотности твердого тела, нерастворимого в воде.

1.Измерить температуру дистиллированной воды и из справочных таблиц

найти плотность воды 0.

2. Определить взвешиванием массу m, выбранных для анализа кусочков твер-

дого тела.

3.Определить массу сухого и чистого пикнометра Мп.

4.Аккуратно, чтобы не осталось капель на стенках горлышка внутри пикно-

метра, наполнить пикнометр жидкостью до метки и взвесить Мпв.

75

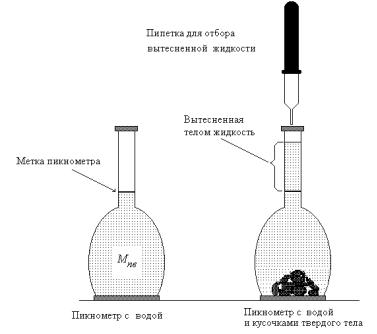
5. Поместить в пикнометр кусочки исследуемого твердого тела, встряхивая,

удалить пузырьки воздуха. Пипеткой удалить воду, вытесненную телом, до метки на пикнометре. Пикнометр с оставшейся водой и твердыми телами взве-

сить Мпвт.

Рис. 6.1

6.Все опыты провести для трех разных по массе тел m1, m2, m3.

7.Результаты измерений занести в таблицу

8.Провести статистическую обработку результатов измерений.

Результаты измерений

№ п/п

m

M п

М пв

Мпвт

1.

2.

3.

76

II. Определение плотности жидкости

Используя сделанные выше рассуждения, выведете формулу для опреде-

ления плотности жидкости.

Массы пустого пикнометра М п и пикнометра с водой М пв возьмем из предыдущих опытов.

Масса воды в пикнометре mв= Мпв – Мпв (6.2)

Обозначим через М ж массу пикнометра с исследуемой жидкостью, тогда по аналогии с (6.2), масса исследуемой жидкости:

m ж = М ж – М п .

Используем формулу (6.1), откуда объём воды: V в =

mв

, а объём иссле-

о

дуемой жидкости: Vж

mж

. Так как объёмы воды и исследуемой жидкости

ж

равны V в = V ж , то:

m

m

и ж

m

.

в

ж

о

ж

m

о

ж

в

Выполнение работы

Заполните пикнометр исследуемой жидкостью до метки, взвесьте и зане-

сите в таблицу значение М ж. Опыт повторить трижды.

Таблица 2

№ п/п

М п

М пв

М ж

1.

Примечание: значения М п и Мпв взять из первого опыта.

77

РАБОТА № 8. ОПЫТНОЕ ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗА

Актуальность работы:

Коэффициент Пуассона – это отношение теплоёмкости газа при постоян-

ном давлении к теплоёмкости газа при постоянном объёме. Эта величина зави-

сит от числа степеней свободы газа и является одной из характеристик газа.

Цель работы:

Определение отношения теплоемкостей газа (коэффициент Пуассона) ме-

тодом Клемана-Дезорма.

Целевые задачи:

знать: уравнение Менделеева-Клайперона, изопроцессы, определение теп-

лоёмкости, теплоёмкости газов в любом изопроцессе

уметь: определять отношения теплоемкостей газа (коэффициент Пуассона)

методом Клемана-Дезорма.

План подготовки конспекта:

1.Основные теоретические сведения

2.Выяснить, что измеряется в лабораторной работе, каким методом и для

чего.

2.Подготовить таблицу.

3.Записать расчётную формулу.

Вопросы для подготовки к входному тестированию:

1.Первое начало термодинамики.

2.Удельная теплоемкость. Связь между удельными теплоемкостями.

3.Молярная теплоемкость при постоянном объеме.

4.Молярная теплоемкость при постоянном давлении.

5.Почему Cp, больше Cv?

6.Какой процесс называется адиабатическим?

7.Что происходит с внутренней энергией газа и его температурой при адиабатическом расширении, при адиабатическом сжатии?

78

8.Чему равна внутренняя энергия газа?

9.В какой момент вашей работы происходит адиабатический процесс,

изохорический процесс, объясните на графике.

10.Почему кран открывается на короткий промежуток времени? 11.Какие значения принимает i для 1, 2 и 3 атомных газов.

12.Какое влияние на результат опыта окажет присутствие водяного пара.

Теоретические сведения

Любое состояние газа можно характеризовать тремя основными парамет-

рами: давлением (Р), объемом (V) и температурой (Т). Уравнение, которое свя-

зывает эти параметры, называется уравнением состояния газа. Таким уравнени-

ем для идеального газа является уравнение Менделеева – Клапейрона:

PV=nRT,

где n – число молей в объеме V.

Зная массу газа и его молекулярный вес , можно определить число молей n, содержащихся в этом объеме:

n m , тогда

PV

m

PT .

(8.1)

Для одного моля n = 1 уравнение имеет вид:

PV=RT , (8.2)

где R – универсальная газовая постоянная, ее численное значение опреде-

ляется соотношением:

R= P0V0 ,

T0

где P0 = 1атм., V0 = 22,4 литра (это объем, занимаемый одним молем газа при Т0 = 2730 К).

В системе СИ R = 8,31.103 дж/кмоль градус. В калориях R 2

кал/моль градус.

Теплоемкость газа зависит от условий нагревания газа. Удельная теплоем-

79

кость газа c – количество тепла, которое необходимо подвести к единице массы вещества, чтобы повысить его температуру на один градус. Ее можно опреде-

лить, воспользовавшись выражением:

Q= сm Т,

откуда с =

Q

.

(8.3)

m T

Молярная теплоемкость «C» – количество тепла, которое необходимо под-

вести к одному молю вещества, чтобы повысить его температуру на один гра-

дус. Она связана с удельной теплоемкостью соотношением:

С= с,

С =

Q

.

(8.4)

m

T

Чтобы определить значение теплоемкости в разных процессах, воспользу-

емся первым началом термодинамики.

1-е начало термодинамики. Теплота, подводимая к газу, расходуется на увеличение внутренней энергии газа U и на работу совершаемую газом против внешних сил.

Q= U+A

(8.5)

Внутренняя энергия идеального газа равна:

U =

i

m

RT ,

(8.6)

2

где i – число степеней свободы молекулы газа. Эта величина отражает ко-

личество координат характеризующих положение частицы в пространстве. Ее изменение равно

U =

i

m

R T

(8.7)

2

Внутренняя энергия газа изменяется при изменении температуры газа.

Элементарная работа, совершаемая газом, равна:

A=P V или dА=PdV (8.8)

В формулу, определяющую молярную теплоемкость (8.4), подставим вы-

ражение (8.5):

C=

U

A

(8.9)

m

T

T

80

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

Источник
Плотность
{displaystyle rho ={frac {M}{V}}}
Размерность L−3 M
Единицы измерения
СИ кг/м³
СГС г/см³
Примечания
скалярная величина

Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму или как производная массы по объёму:

{displaystyle rho ={frac {M}{V}},qquad rho ={frac {dm}{dV}}}.

Данные выражения не эквивалентны, и выбор зависит от того, какая именно плотность рассматривается. Различаются:

Для точечной массы плотность является бесконечной. Математически её можно определить или как меру, или как производную Радона — Никодима по отношению к некоторой опорной мере.

Для обозначения плотности обычно используется греческая буква rho (ро) (происхождение обозначения подлежит уточнению), иногда используются латинские буквы D и d (от лат. densitas «плотность»). Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.

Понятие «плотность» в физике может иметь более широкую трактовку. Существуют поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам. Кроме того, говорят не только о плотности массы, но и о плотности других величин, например энергии, электрического заряда. В таких случаях к термину «плотность» добавляются конкретизирующие слова, скажем «линейная плотность заряда». «По умолчанию» под плотностью понимается вышеуказанная (трёхмерная, кг/м³) плотность массы.

Формула нахождения плотности[править | править код]

Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:

{displaystyle rho ={frac {M}{V}},}

где M — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.

При вычислении плотности газов при стандартных условиях эта формула может быть записана и в виде:

{displaystyle rho ={frac {M_{mol}}{V_{mol}}},}

где {displaystyle M_{mol}} — молярная масса газа, {displaystyle V_{mol}} — молярный объём (при стандартных условиях приближённо равен 22,4 л/моль).

Плотность тела в точке записывается как

rho ={frac {dm}{dV}},

тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как

{displaystyle M=int rho (mathbf {r} )d^{3}mathbf {r} =int rho (mathbf {r} )dV=int dm.}

Случай сыпучих и пористых тел[править | править код]

В случае сыпучих и пористых тел различают

  • истинную плотность, определяемую без учёта пустот;
  • насыпную плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму.

Истинную плотность из насыпной (кажущейся) получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме.

Зависимость плотности от температуры[править | править код]

Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.

При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.

Диапазон плотностей в природе[править | править код]

Для различных природных объектов плотность меняется в очень широком диапазоне.

  • Самую низкую плотность имеет межгалактическая среда (2·10−31—5·10−31 кг/м³, без учёта тёмной материи)[2].
  • Плотность межзвёздной среды приблизительно равна 10−23—10−21 кг/м³.
  • Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
  • Плотность газообразного водорода (самого лёгкого газа) при стандартных условиях равна 0,0899 кг/м³.
  • Плотность сухого воздуха при стандартных условиях составляет 1,293 кг/м³.
  • Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
  • Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
  • Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
  • Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
  • Плотность пресной воды при 4 °C 1000 кг/м³.
  • Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
  • Гранит имеет плотность 2600 кг/м³.
  • Средняя плотность Земли равна 5520 кг/м³.
  • Плотность железа равна 7874 кг/м³.
  • Плотность металлического урана 19100 кг/м³.
  • Плотность золота 19320 кг/м³.
  • Плотность нептуния — самого плотного актиноида — 20200 кг/м³.
  • Самые плотные вещества при стандартных условиях — металлы платиновой группы шестого периода (осмий, иридий, платина), а также рений. Имеют плотность 21000—22700 кг/м³.
  • Плотность атомных ядер приблизительно 2·1017 кг/м³.
  • Теоретически верхняя граница плотности по современным[когда?] физическим представлениям — это планковская плотность 5,1⋅1096 кг/м³.

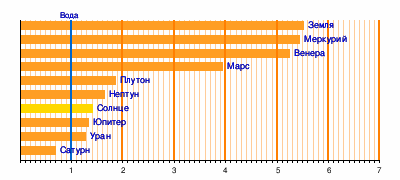
Плотности астрономических объектов[править | править код]

Средняя плотность небесных тел Солнечной
системы (в г/см³)[3][4][5]

  • Средние плотности небесных тел Солнечной системы см. на врезке.
  • Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.
  • Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
  • Плотность межгалактической среды 2×10−34÷5×10−34 кг/м³.
  • Средняя плотность красных гигантов на много порядков меньше чем у Солнца из-за того, что их радиус в сотни раз больше.
  • Плотность белых карликов 108÷1012 кг/м³
  • Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
  • Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:
rho ={frac {3,c^{6}}{32pi M^{2}G^{3}}}.
Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M−2). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 1019 кг/м³, превышающей ядерную плотность (2×1017 кг/м³), то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).

Плотности некоторых газов[править | править код]

Плотность газов, кг/м³ при НУ.

Азот 1,250 Кислород 1,429
Аммиак 0,771 Криптон 3,743
Аргон 1,784 Ксенон 5,851
Водород 0,090 Метан 0,717
Водяной пар (100 °C) 0,598 Неон 0,900
Воздух 1,293 Радон 9,81
Гексафторид вольфрама 12,9 Углекислый газ 1,977
Гелий 0,178 Хлор 3,164
Дициан 2,38 Этилен 1,260

Для вычисления плотности произвольного идеального газа, находящегося в произвольных условиях, можно использовать формулу, выводящуюся из уравнения состояния идеального газа:[6]

{displaystyle rho ={frac {pM_{mol}}{RT}}},

где:

Плотности некоторых жидкостей[править | править код]

Плотность жидкостей, кг/м³

Бензин 710 Молоко 1040
Вода (4 °C) 1000 Ртуть (0 °C) 13600
Керосин 820 Диэтиловый эфир 714
Глицерин 1260 Этанол 789
Морская вода 1030 Скипидар 860
Масло оливковое 920 Ацетон 792
Масло моторное 910 Серная кислота 1835
Нефть 550—1050 Жидкий водород (−253 °C) 70

Плотность некоторых пород древесины[править | править код]

Плотность древесины, г/см³

Бальса 0,15 Пихта сибирская 0,39
Секвойя вечнозелёная 0,41 Ель 0,45
Ива 0,46 Ольха 0,49
Осина 0,51 Сосна 0,52
Липа 0,53 Конский каштан 0,56
Каштан съедобный 0,59 Кипарис 0,60
Черёмуха 0,61 Лещина 0,63
Грецкий орех 0,64 Берёза 0,65
Вишня 0,66 Вяз гладкий 0,66
Лиственница 0,66 Клён полевой 0,67
Тиковое дерево 0,67 Бук 0,68
Груша 0,69 Дуб 0,69
Свитения (Махагони) 0,70 Платан 0,70
Жостер (крушина) 0,71 Тис 0,75
Ясень 0,75 Слива 0,80
Сирень 0,80 Боярышник 0,80
Пекан (кария) 0,83 Сандаловое дерево 0,90
Самшит 0,96 Эбеновое дерево 1,08
Квебрахо 1,21 Бакаут 1,28
Пробка 0,20

Плотность некоторых металлов[править | править код]

Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.

Плотность металлов, кг/м³

Осмий 22610[7] Родий 12410[8] Хром 7190[9]
Иридий 22560[10] Палладий 12020[11] Германий 5320[12]
Плутоний 19840[13] Свинец 11350[14] Алюминий 2700[15]
Платина 19590[16] Серебро 10500[17] Бериллий 1850[18]
Золото 19300[14] Никель 8910[19] Рубидий 1530[20]
Уран 19050[21] Кобальт 8860[22] Натрий 970[23]
Тантал 16650[24] Медь 8940[25] Цезий 1840[26]
Ртуть 13530[27] Железо 7870[28] Калий 860[29]
Рутений 12450[30] Марганец 7440[31] Литий 530[32]

Измерение плотности[править | править код]

Для измерений плотности используются:

  • Пикнометр — прибор для измерения истинной плотности
  • Различные виды ареометров — измерители плотности жидкостей.
  • Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
  • Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
  • Метод гидростатического взвешивания.

Остеоденситометрия — процедура измерения плотности костной ткани человека.

См. также[править | править код]

Видеоурок: плотность вещества

  • Список химических элементов с указанием их плотности
  • Удельный вес
  • Удельная плотность
  • Относительная плотность
  • Объёмная плотность
  • Конденсация
  • Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
  • Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
  • Концентрация частиц
  • Концентрация растворов
  • Плотность заряда
  • Уравнение неразрывности

Примечания[править | править код]

  1. ↑ Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
  2. ↑ Агекян Т. А. . Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
  3. ↑ Planetary Fact Sheet Архивировано 14 марта 2016 года. (англ.)
  4. ↑ Sun Fact Sheet Архивная копия от 15 июля 2010 на Wayback Machine (англ.)
  5. ↑ Stern, S. A., et al. The Pluto system: Initial results from its exploration by New Horizons (англ.) // Science : journal. — 2015. — Vol. 350, no. 6258. — P. 249—352. — doi:10.1126/science.aad1815.
  6. ↑ МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА. Учебно-методическое пособие к лабораторным работам № 1-51, 1-61, 1-71, 1-72. Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров (2014). Дата обращения: 4 января 2019. Архивировано 23 ноября 2018 года.
  7. ↑ Krebs, 2006, p. 158.
  8. ↑ Krebs, 2006, p. 136.
  9. ↑ Krebs, 2006, p. 96.
  10. ↑ Krebs, 2006, p. 160.
  11. ↑ Krebs, 2006, p. 138.
  12. ↑ Krebs, 2006, p. 198.
  13. ↑ Krebs, 2006, p. 319.
  14. ↑ 1 2 Krebs, 2006, p. 165.
  15. ↑ Krebs, 2006, p. 179.
  16. ↑ Krebs, 2006, p. 163.
  17. ↑ Krebs, 2006, p. 141.
  18. ↑ Krebs, 2006, p. 67.
  19. ↑ Krebs, 2006, p. 108.
  20. ↑ Krebs, 2006, p. 57.
  21. ↑ Krebs, 2006, p. 313.
  22. ↑ Krebs, 2006, p. 105.
  23. ↑ Krebs, 2006, p. 50.
  24. ↑ Krebs, 2006, p. 151.
  25. ↑ Krebs, 2006, p. 111.
  26. ↑ Krebs, 2006, p. 60.
  27. ↑ Krebs, 2006, p. 168.
  28. ↑ Krebs, 2006, p. 101.
  29. ↑ Krebs, 2006, p. 54.
  30. ↑ Krebs, 2006, p. 134.
  31. ↑ Krebs, 2006, p. 98.
  32. ↑ Krebs, 2006, p. 47.

Литература[править | править код]

  • Плотность — статья из Большой советской энциклопедии.  — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
  • Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
  • Krebs R. E. . The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.

Ссылки[править | править код]

  • Онлайн интерактивная таблица плотности веществ Архивная копия от 29 апреля 2011 на Wayback Machine (рус.)
  • Подробная таблица значений плотности распространенных жидкостей Архивная копия от 5 октября 2016 на Wayback Machine (рус.)
  • Урок по теме “Плотность вещества” Архивная копия от 30 января 2022 на Wayback Machine
Источник
Плотность
rho ={frac {m}{V}}
Размерность L−3 M
Единицы измерения
СИ кг/м³
СГС г/см³
Примечания
скалярная величина

Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму[1].

Для обозначения плотности обычно используется греческая буква ρ (ро) (происхождение обозначения подлежит уточнению), иногда используются также латинские буквы D и d (от лат. densitas — «плотность»).

Более точное определение плотности требует уточнение формулировки:

  • Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
  • Плотность вещества — это плотность однородного или равномерно неоднородного тела, состоящего из этого вещества.
  • Плотность тела в точке — это предел отношения массы малой части тела (Delta m), содержащей эту точку, к объёму этой малой части ({displaystyle Delta V}), когда этот объём стремится к нулю[2], или, записывая кратко, {displaystyle lim _{Delta Vto 0}{Delta m/Delta V}}. При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.

Поскольку масса в теле может быть распределена неравномерно, более адекватная модель определяет плотность в каждой точке тела как производную массы по объёму. Если учитывать точечные массы, то плотность можно определить как меру, либо как производную Радона—Никодима по отношению к некоторой опорной мере.

Содержание

  • 1 Виды плотности и единицы измерения
  • 2 Формула нахождения плотности
  • 3 Зависимость плотности от температуры
  • 4 Диапазон плотностей в природе
  • 5 Плотности астрономических объектов
  • 6 Плотности некоторых газов
  • 7 Плотности некоторых жидкостей
  • 8 Плотность некоторых пород древесины
  • 9 Плотность некоторых металлов
  • 10 Измерение плотности
  • 11 См. также
  • 12 Примечания
  • 13 Литература
  • 14 Ссылки

Виды плотности и единицы измерения

Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.

Для сыпучих и пористых тел различают:

  • истинную плотность, определяемую без учёта пустот;
  • удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму. Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме. Для сыпучих тел удельная плотность называется насыпно́й плотностью.

Формула нахождения плотности

Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:

rho ={frac {m}{V}},

где m — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.

  • При вычислении плотности газов при нормальных условиях эта формула может быть записана и в виде:
rho ={frac {M}{V_{m}}},
где М — молярная масса газа, V_{m} — молярный объём (при нормальных условиях приближённо равен 22,4 л/моль).

Плотность тела в точке записывается как

rho ={frac {dm}{dV}},

тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как

m=int rho ({mathbf r})d^{3}{mathbf r}=int rho ({mathbf r})dV=int dm.

Зависимость плотности от температуры

Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.

При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.

Диапазон плотностей в природе

Для различных природных объектов плотность меняется в очень широком диапазоне.

  • Самую низкую плотность имеет межгалактическая среда (2·10−31—5·10−31 кг/м³, без учёта тёмной материи)[3].
  • Плотность межзвёздной среды приблизительно равна 10−23—10−21 кг/м³.
  • Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
  • Плотность газообразного водорода (самого лёгкого газа) при нормальных условиях равна 0,0899 кг/м³.
  • Плотность сухого воздуха при нормальных условиях составляет 1,293 кг/м³.
  • Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
  • Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
  • Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
  • Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
  • Плотность пресной воды при 4 °C 1000 кг/м³.
  • Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
  • Гранит имеет плотность 2600 кг/м³.
  • Средняя плотность Земли равна 5520 кг/м³.
  • Плотность железа равна 7874 кг/м³.
  • Плотность металлического урана 19100 кг/м³.
  • Плотность атомных ядер приблизительно 2·1017 кг/м³.
  • Теоретически верхняя граница плотности по современным физическим представлениям это планковская плотность 5,1·1096 кг/м³.

Плотности астрономических объектов

Средняя плотность небесных тел Солнечной
системы (в г/см³)[4][5][6]

  • Средние плотности небесных тел Солнечной системы см. на врезке.
  • Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.
  • Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
  • Плотность межгалактической среды 2×10−34÷5×10−34 кг/м³.
  • Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
  • Плотность белых карликов 108÷1012 кг/м³
  • Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
  • Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:
rho ={frac {3,c^{6}}{32pi M^{2}G^{3}}}.
Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M−2). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 1019 кг/м³, превышающей ядерную плотность (2×1017 кг/м³), то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).

Плотности некоторых газов

Плотность газов, кг/м³ при НУ.

Азот 1,250 Кислород 1,429
Аммиак 0,771 Криптон 3,743
Аргон 1,784 Ксенон 5,851
Водород 0,090 Метан 0,717
Водяной пар (100 °C) 0,598 Неон 0,900
Воздух 1,293 Радон 9,81
Гексафторид вольфрама 12,9 Углекислый газ 1,977
Гелий 0,178 Хлор 3,164
Дициан 2,38 Этилен 1,260

Плотности некоторых жидкостей

Плотность жидкостей, кг/м³

Бензин 710 Молоко 1040
Вода (4 °C) 1000 Ртуть (0 °C) 13600
Керосин 820 Эфир 720
Глицерин 1260 Спирт 800
Морская вода 1030 Скипидар 860
Масло оливковое 920 Ацетон 792
Масло моторное 910 Серная кислота 1840
Нефть 550—1050 Жидкий водород (−253 °C) 70

Плотность некоторых пород древесины

Плотность древесины, г/см³

Бальса 0,15 Пихта сибирская 0,39
Секвойя вечнозелёная 0,41 Ель 0,45
Ива 0,46 Ольха 0,49
Осина 0,51 Сосна 0,52
Липа 0,53 Конский каштан 0,56
Каштан съедобный 0,59 Кипарис 0,60
Черёмуха 0,61 Лещина 0,63
Грецкий орех 0,64 Берёза 0,65
Вишня 0,66 Вяз гладкий 0,66
Лиственница 0,66 Клён полевой 0,67
Тиковое дерево 0,67 Бук 0,68
Груша 0,69 Дуб 0,69
Свитения (Махагони) 0,70 Платан 0,70
Жостер (крушина) 0,71 Тис 0,75
Ясень 0,75 Слива 0,80
Сирень 0,80 Боярышник 0,80
Пекан (кария) 0,83 Сандаловое дерево 0,90
Самшит 0,96 Эбеновое дерево 1,08
Квебрахо 1,21 Бакаут 1,28
Пробка 0,20

Плотность некоторых металлов

Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.

Плотность металлов, г/см³

Осмий 22,61[7] Родий 12,41[8] Хром 7,19[9]
Иридий 22,56[10] Палладий 12,02[11] Германий 5,32[12]
Плутоний 19,84[13] Свинец 11,35[14] Алюминий 2,70[15]
Платина 19,59[16] Серебро 10,50[17] Бериллий 1,85[18]
Тантал 19,30[19] Медь 8,94[20] Цезий 1,84[21]
Золото 19,30[14] Никель 8,91[22] Рубидий 1,53[23]
Уран 19,05[24] Кобальт 8,86[25] Натрий 0,97[26]
Ртуть 13,53[27] Железо 7,87[28] Калий 0,86[29]
Рутений 12,45[30] Марганец 7,44[31] Литий 0,53[32]

Измерение плотности

Для измерений плотности используются:

  • Пикнометр — прибор для измерения истинной плотности
  • Различные виды ареометров — измерители плотности жидкостей.
  • Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
  • Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.

См. также

Видеоурок: плотность вещества

  • Список химических элементов с указанием их плотности
  • Удельный вес
  • Удельная плотность
  • Относительная плотность
  • Объёмная плотность
  • Конденсация
  • Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
  • Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
  • Концентрация частиц
  • Концентрация растворов
  • Плотность заряда
  • Уравнение неразрывности

Примечания

  1. ↑ Существуют также поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам.
  2. ↑ Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
  3. ↑ Агекян Т. А.  Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
  4. ↑ Planetary Fact Sheet (англ.)
  5. ↑ Sun Fact Sheet (англ.)
  6. ↑ Stern, S. A., et al. (2015). «The Pluto system: Initial results from its exploration by New Horizons». Science 350 (6258): 249–352. DOI:10.1126/science.aad1815.
  7. ↑ Krebs, 2006, p. 158.
  8. ↑ Krebs, 2006, p. 136.
  9. ↑ Krebs, 2006, p. 96.
  10. ↑ Krebs, 2006, p. 160.
  11. ↑ Krebs, 2006, p. 138.
  12. ↑ Krebs, 2006, p. 198.
  13. ↑ Krebs, 2006, p. 319.
  14. ↑ 1 2 Krebs, 2006, p. 165.
  15. ↑ Krebs, 2006, p. 179.
  16. ↑ Krebs, 2006, p. 163.
  17. ↑ Krebs, 2006, p. 141.
  18. ↑ Krebs, 2006, p. 67.
  19. ↑ Krebs, 2006, p. 151.
  20. ↑ Krebs, 2006, p. 111.
  21. ↑ Krebs, 2006, p. 60.
  22. ↑ Krebs, 2006, p. 108.
  23. ↑ Krebs, 2006, p. 57.
  24. ↑ Krebs, 2006, p. 313.
  25. ↑ Krebs, 2006, p. 105.
  26. ↑ Krebs, 2006, p. 50.
  27. ↑ Krebs, 2006, p. 168.
  28. ↑ Krebs, 2006, p. 101.
  29. ↑ Krebs, 2006, p. 54.
  30. ↑ Krebs, 2006, p. 134.
  31. ↑ Krebs, 2006, p. 98.
  32. ↑ Krebs, 2006, p. 47.

Литература

  • Плотность — статья из Большой советской энциклопедии.  — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
  • Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
  • Krebs R. E.  The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.

Ссылки

  • Онлайн интерактивная таблица плотности веществ (рус.)
  • Подробная таблица значений плотности распространенных жидкостей (рус.)
Источник

Ключевые ситуации при изучении физики. Сплавы

Наибольшие трудности при изучении физики учащиеся испытывают при решении задач, т.е. когда требуется применить знания. Эти трудности представляются ребятам настолько большими, что многие из них отказываются даже от попыток решать задачи. Отказ от решения задач еще как-то «проходил» во времена устных экзаменов по физике. Но теперь – как при прохождении Государственной итоговой аттестации, выполнении заданий Единого государственного экзамена или тестирования при поступлении – проверяют именно умение применять полученные знания, а не декларировать их.

Понимание смысла физических законов – главная цель школьного курса физики, но понимание этих законов может родиться только в осознанной деятельности по применению этих законов. Школьникам же часто предлагают алгоритмы решения задач, которые провоцируют бездумное, автоматическое применение физических формул.
Преодолеть эту принципиальную трудность можно, только неоднократно применяя законы физики в тщательно отобранных простейших ситуациях, когда смысл этих законов кристально ясен.

В школьном курсе физики тысячи задач. Однако, если посмотреть на все множество этих задач «с высоты птичьего полета», то нетрудно заметить, что подавляющее их большинство группируются вокруг нескольких десятков типичных учебных ситуаций. Эти ситуации можно назвать ключевыми. А овладение ключевыми ситуациями «даст ключи» к решению задач.

Ключевые ситуации – важнейшая связь между «теорией» и «задачами». Без этой связи теория мертва для школьника, а задачи представляются ему случайной россыпью неинтересных загадок. Однако пока еще некоторые учителя «дают» своим ученикам «теорию» отдельно, а «задачи» отдельно. После такого разрезания по живому от живой физики остаются только мертвые формулы-шаблоны для примитивных задач на подстановку.

Изучение ключевых ситуаций – это живой мост между «теорией» и «задачами», причем мост с двухсторонним движением. С одной стороны, задачи рождаются при изучении ключевых ситуаций, в которых наглядно проявляется действие физических законов, с другой стороны, благодаря решению задач на основе ключевой ситуации теория осознается, т.е. становится действенной силой, а не пассивным набором фактов и формул.
И еще одна очень важная роль ключевых ситуаций. Дело в том, что результатом изучения школьного курса физики должен быть не набор решенных задач (это быстро забывается), а понимание физических законов и физическая интуиция, которая может развиваться именно при рассмотрении ключевых ситуаций.

Приложение 1. Фрагмент урока с выделением ключевой ситуации по теме «Плотность».
Приложение 2. Фрагмент урока с выделением ключевой ситуации по теме «Полые тела».
Приложение 3. Дополнительный материал по теме «Сплавы».

Приведем фрагмент урока с выделение ключевой ситуации по теме «Сплавы».

Фрагмент урока по теме «СПЛАВЫ»

Учитель. Тема урока зашифрована ребусом. Кто первый раскроет секрет?

Ученики. …

Учитель. Тема урока «Сплавы».
Сплав — макроскопически однородная смесь двух или большего числа химических элементов с преобладанием металлических компонентов. Основной или единственной фазой сплава, как правило, является твёрдый раствор легирующих элементов в металле, являющемся основой сплава.
Сплавы имеют металлические свойства, например: металлический блеск, высокие электропроводность и теплопроводность. Иногда компонентами сплава могут быть не только химические элементы, но и химические соединения, обладающие металлическими свойствами. Например, основными компонентами твёрдых сплавов являются карбиды вольфрама или титана. Макроскопические свойства сплавов всегда отличаются от свойств их компонентов, а макроскопическая однородность многофазных (гетерогенных) сплавов достигается за счёт равномерного распределения примесных фаз в металлической матрице.
Сплавы обычно получают с помощью смешивания компонентов в расплавленном состоянии с последующим охлаждением. При высоких температурах плавления компонентов, сплавы производятся смешиванием порошков металлов с последующим спеканием (так получаются, например, многие вольфрамовые сплавы).
Сплавы являются одним из основных конструкционных материалов. Среди них наибольшее значение имеют сплавы на основе железа и алюминия. В состав многих сплавов могут вводиться и неметаллы, такие как углерод, кремний, бор и др. В технике применяется более 5 тыс. сплавов.

Цель нашего урока – научиться решать задачи для определения плотности, массы или объема сплавов или веществ входящих в их состав.
Рассматривая сплавы, обычно предполагают, что объем сплава равен сумме объемов составляющих его веществ. В таком случае плотность сплава , где индексы 1 и 2 относятся к двум компонентам сплава.
Если заданы или требуется найти массы компонентов известной плотности ρ1 и ρ2, то объемы компонентов надо выразить через их массы и плотности, в результате чего формула для плотности сплава примет вид .
Часто в задаче дано или требуется найти соотношение масс компонентов сплава. Обозначим . Тогда . Эта формула связывает плотность сплава ρ и массовое отношение компонент . Из нее при следует: . Приведенные формулы позволяют по заданному значению одной из величин ( или ρ) найти значение другой.

Запишите в тетрадях:

Примечание.

1. Задача первого уровня предназначена для применения основной формулы: .
2. Задачи второго уровня похожи, поэтому целесообразно применить разные способы решения.
3. Задачи третьего уровня предусмотрены для закрепления способов решения задач предложенных ранее с добавлением дополнительных вычислений (объема и процентного отношения).

РЕШЕНИЕ ЗАДАЧ

Задачи по теме «СПЛАВЫ»:

Найдите плотность бронзы, для изготовления которой взяли 100 г меди и 30 г олова, считая, что объем сплава равен сумме объемов входящих в него металлов.

1. Кусок сплава из свинца и олова массой 664 г имеет плотность 8,3 г/см 3 . Определите массу свинца в сплаве. Принять объем сплава равным сумме объемов его составных частей.

2. В куске кварца содержится небольшой самородок золота. Масса куска 100 г, а его плотность 8 г/см 3 . Определите массу золота, содержащегося в кварце. Принять, что плотность кварца и золота соответственно равны 2,65 и 19,36 г/см 3 .

1. Сплав золота и серебра массой 400 г имеет плотность 14·103 кг/м 3 . Полагая объем сплава равным сумме объемов его составных частей, определите массу, объем золота и процентное содержание его в сплаве.

2. В чистой воде растворена кислота. Масса раствора 240 г, а его плотность 1,2 г/см 3 . Определите объем кислоты в растворе и его процентное содержание, если плотность кислоты 1,8 г/см 3 . Принять объем раствора равным сумме объемов его составных частей.

Выходной контроль:

1 А соотношение масс
2 Б плотность сплава, если известны соотношения масс
3 В процентное содержание массы одного из веществ в сплаве
4 Г процентное содержание объема одного из веществ в сплаве
5 Д плотность сплава
6 Е объем кварца
7 Ж плотность сплава, при заданных плотностях веществ его составляющих

Ответы: 1-Д, 2-Ж, 3-А, 4-Б, 5-В. 6-Г, 7-Е.

Домашнее задание:

Сплавы различаются по своему предназначению.
Конструкционные сплавы: стали, чугуны, дюралюминий.
Конструкционные со специальными свойствами (например, искробезопасность, антифрикционные свойства): бронзы, латуни.
Для заливки подшипников: баббит.
Для измерительной и электронагревательной аппаратуры: манганин, нихром.
Для изготовления режущих инструментов: победит.

Подготовьте сообщение о каком-нибудь сплаве. Расскажите о веществах, которые в него входят, о их процентном вхождении в сплав и т.д.

Задачи:

1. Найдите плотность стали (сталь — деформируемый (ковкий) сплав железа с углеродом), для изготовления которой взяли 100 г железа и 2 г углерода (углекислого газа), считая, что объем сплава равен сумме объемов входящих в него веществ.
2. Чтобы получить латунь, сплавили куски меди массой 178 кг и цинка массой 355 кг. Какой плотности была получена латунь? Объем сплава равен сумме объемов его составных частей.
3. Сплав золота и серебра массой 500 г имеет плотность 11 г/см3. Полагая объем сплава равным сумме объемов его составных частей, определите массу, объем золота и процентное содержание его в сплаве.

Ответы: 1. 0,098 г/см 3 , 2. 8540 кг/м 3 , 3. 50 г, 2,59 см 3 , 10%.

Подведение итогов урока. Рефлексия

На полях рабочей тетради изобрази схематически один из рисунков, который соответствует степени усвоения материала на уроке. Солнце – мне все понятно, туча – материал интересный, но надо еще поработать, луна – я все проспал.

Статья «Решение задач на нахождение плотности смесей и сплавов, средней плотности неоднородных тел» (7 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Решение задач на нахождение плотности смесей и сплавов,

средней плотности неоднородных тел (7 класс)

Ларионов Вадим Сергеевич,

учитель физики МБОУ Лицея № 15 г.Сарова, larionvadim @ yandex . ru

Ларионова Наталья Валентиновна,

В статье сформулированы методические рекомендации по организации факультативного занятия по решению задач на нахождение плотности смесей, сплавов и неоднородных тел. Представлены учебные материалы по теме, структурированные по уровню сложности.

Задачи на нахождение плотности смеси или сплава, средней плотности неоднородного («составного») тела являются базовыми при изучении темы «Плотность» и достаточно часто встречаются в олимпиадах по физике в 7-8-х классах. Именно поэтому целесообразно данному типу задач посвятить отдельное факультативное занятие, структура которого соответствует принципу «от простого к сложному» и содержит последовательные блоки задач: ключевые, олимпиадные и задачи для самостоятельного решения (см. приложение).

Средняя плотность неоднородного («составного») тела, плотность смеси или сплава рассчитывается по формуле

где m 1 , m 2 , m 3 … -массы отдельных частей тела (компонентов смеси или сплава), а V 1 , V 2 , V 3 … — их объёмы.

Для решения задач по данной теме, необходимо составить систему уравнений, в основе которой лежат следующие положения:

1. Определительная формула плотности

2. Свойство аддитивности массы (масса смеси или сплава равна сумме масс его составных частей)

m=m 1 + m 2 + m 3 +…

3. Как правило, в таких задачах полагают, что объём сплава (смеси) равен сумме объёмов его составных частей

V = V 1 + V 2 + V 3 …

В задачах, предложенных ниже, исключением является задача № 6 из блока олимпиадных задач (задача о смешивании спирта и воды).

Ключевые задачи, представленные в занятии, в зависимости от подготовки учащихся могут быть решены непосредственно на уроке при изучении темы «Плотность». В этом случае на факультативном занятии рассматриваются олимпиадные задачи. Далее ученикам предлагаются задачи для самостоятельного решения, которые, как правило, составляют домашнее задание. В этом случае удобно дифференцировать домашнее задание учеников, предложив не более трёх обязательных задач в зависимости от уровня подготовленности учеников. Учитель может дополнить списки олимпиадных задач и задач для самостоятельного решения, используя материалы последних олимпиад.

Плотность смесей, сплавов, «составных» тел

Цель: Научиться решать задачи на нахождение плотности смесей и сплавов, а также средней плотности неоднородных тел («составных») тел.

Ключевые задачи

1. Какова плотность сплава из 300г олова и 100г свинца? (8г / см 3 )

2. Сплав изготовлен из меди объёмом 0,4 м 3 и цинка массой 710 кг. Какова плотность сплава? (8540 кг/м 3 )

3. Для приготовления вишнёвого сиропа в кастрюлю вылили 1 л вишнёвого варенья и 2 л воды и хорошо перемешали. Какова плотность сиропа, если плотность варенья 1300 кг/м 3 ? (1100 кг/м 3 )

4. Какова плотность смеси из глицерина и спирта, если объём спирта составляет половину объёма смеси? Как изменится ответ, если масса спирта составляет половину массы смеси? (1030 кг / м 3 , 980 кг / м 3 )

Олимпиадные задачи

1. Масса первого изделия в 2 раза больше массы второго изделия, а их объёмы находятся в отношении V 1 : V 2 =1:3. Плотность первого изделия ρ1=4г/см 3 . Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой и объёмом клея пренебречь. (1,5 г/см 3 )

2. Изделие, склеенное из трёх различных частей, имеет объём V =600см 3 . Объёмы частей находятся в соотношении V 1 : V 2 : V 3 =2:3:5, а их плотности – в соотношении ρ1:ρ2:ρ3=4:3:1. Чему равна масса изделия, если плотность первой части ρ1=2000кг/м 3 ? (660 г)

3. Ученик измерил плотность деревянного бруска, покрытого краской, и она оказалась равной ρ=600 кг/м 3 . Но на самом деле брусок состоит из двух частей, равных по массе, плотность одной из которых в два раза больше плотности другой. Найдите плотности обеих частей бруска. Массой краски можно пренебречь. (450 кг/м 3 , 900 кг/м 3 )

4. В дистиллированную воду аккуратно вливают серную кислоту. Получившийся раствор имеет плотность ρр=1200 кг/м 3 и массу m =120г. Объём раствора равен сумме объёмов воды и кислоты. Плотность воды ρв=1000 кг/м 3 , плотность кислоты ρк=1800 кг/м 3 . Какова масса кислоты, влитой в воду? (45 г)

5. Однородный кубик со стороной a и плотностью ρ поместили внутрь куска глины с плотностью 4ρ, которому придали форму куба со стороной 2a. Получившийся куб облепили пластилином плотностью 2ρ, в результате чего получился куб со стороной 3a (см. рисунок). Определите среднюю плотность получившейся системы. (67ρ/27≈2 ,5ρ)

6. Плотностью вещества называют отношение массы тела из этого вещества к его объёму. Например, масса 1 см 3 воды составляет 1 г, поэтому плотность воды 1 г/см 3 . Представим, что смешали 100 литров воды и 100 литров спирта плотностью 0,8 г/см 3 , и при смешении оказалось, что суммарный объём уменьшился на 5 процентов. Какова плотность полученного раствора? ( ρ =18/19 г/ c м 3 ≈0,95г/ c м 3 )

Задачи для самостоятельного решения

1. Какую плотность имеет сплав из 270г алюминия и 445г меди? (≈ 4,77 г /c м 3 )

2. Сплав золота и серебра массой 400 г имеет плотность 1,4·10 4 кг/м 3 . Полагая объём сплава равным сумме объёмов его составных частей, определите массу золота в сплаве? (220 г)

3. Масса первого изделия в 3 раза меньше массы второго изделия, а их объёмы находятся в соотношении V 1 : V 2 =2:1. Плотность первого тела ρ1=1,8 г/см 3 . Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой и объёмом клея пренебречь. (4,8 г/см 3 )

4. Изделие, склеенное из трёх различных частей, имеет объём V =900см 3 . Объёмы частей находятся в соотношении V 1 : V 2 : V 3 =5:3:1, а их плотности – в соотношении ρ1:ρ2:ρ3=1:2:5. Чему равна масса изделия, если плотность первой части ρ1=500кг/м 3 ? (800 г)

5. Кубик с ребром a =20см сделан из материала с плотностью ρ=3000кг/м 3 . Однако внутри кубика имеется воздушная полость, поэтому его средняя плотность ρср=1200кг/м 3 . Определите объём этой воздушной полости. Во сколько раз изменится средняя плотность кубика, если полость целиком заполнить водой? Массой воздуха внутри полости можно пренебречь. (4800 см 3 , 1,5)

Литература к занятию

1. Генденштейн Л.Э., Кирик Л.А., Гельгафт И.М. Задачи по физике с примерами решений. 7-9 классы. Под ред. В.А.Орлова. – М.: Илекса, 2009. – 416 с.

2. Бажанский И.И., Гой В.А., Чубов Ю.Б. Приморские олимпиады школьников по физике (2003-2007 гг). Учебное пособие. – Владивосток: Изд-во Дальневост. ун-та, 2008. – 200с.

3. Олимпиады 2008-2009. Физика. Задачи Московских олимпиад школьников. Под ред. М.В.Семёнова, А.А.Якуты. – М.: МЦНМО, 2009. – 70 с.

4. 400 физических этюдов. Избранные задачи физических олимпиад Санкт-Петербурга. – СПб, 2006. –284 с.

5. Борисов С.Н. Учебное пособие по физике для учащихся 7-го класса. – М.: МИФИ, 2009. – 100 с.

Подготовка к олимпиадам: 7 класс, плотность

Продолжим подготовку к олимпиадам. Сегодня будем решать задачи на тему “плотность”. При смешивании двух веществ сумма их масс дает массу смеси, а вот с объемами все не так очевидно. Если вы в плотно набитое сухим песком ведро попытаетесь налить воды, то в промежутки между песчинками проникнет достаточное ее количество, таким образом, сумма объемов песка и воды – по-прежнему все то же ведро. О том, что сумма объемов не равна объему смеси, может быть сказано в задаче, или об этом придется догадаться.

Задача 1. Определите плотность сплава, состоящего из $2m$ золота и $7m$ серебра. Плотности металлов известны.

Средняя плотность равна

В данном случае можно считать

Задача 2. Определите плотность сплава, состоящего из $2V$ золота и $7V$ серебра. Плотности металлов известны.

Средняя плотность равна

Объем сплава в данном случае равен сумме объемов компонентов.

Задача 3. Известно, что после того, как из канистры объемом 7 л вылили всю воду, там осталось 1,4 мл воды в виде капель на стенках. Затем канистру плотно закрыли пробкой и поставили на солнце. В результате вся вода внутри канистры испарилась. Определите плотность получившегося газа, если первоначальная плотность воздуха равна 1,3 кг/м$^3$.

Пренебрежем объемом капель по сравнению с объемом канистры. Тогда вначале плотность воздуха равна

Где $m_v$ – масса воздуха.

После того, как капли испарились, плотность можно определить как

Где $m_0$ – масса воды.

Ответ: $rho_2=1,5$ кг/м$^3$.

Задача 4. Однородный кубик со стороной a и плотностью $rho$ поместили внутрь куска глины плотностью $4rho$, которой придали форму куба со стороной $2a$. Получившийся куб облепили пластилином плотностью $2rho$, в результате чего получился куб со стороной $3a$ (см. рисунок). Определите среднюю плотность получившейся системы.

Объем получившегося слепка, очевидно, равен $V=(3a)^3=27a^3$.

Определим массу. Масса внутреннего кубика равна

$$m_1=rho V_1=rho a^3$$

Определим массу глины. Ее объем равен $V_2=(2a)^3-a^3$. Тогда

И, наконец, масса пластилина. Объем его будет равен $(3a)^3-(2a)^2=19a^3$, масса

Тогда плотность всего куска

Задача 5. В ведро, доверху заполненное сухим песком массой 8 кг, добавили 4 л воды. В результате вода вся впиталась и не выступила на поверхность песка. Определите среднюю плотность получившегося сырого песка. Объем ведра 8 литров.

Вот тот случай, когда при смешивании компонентов $Vneq V_1+V_2$.

Плотность будет равна ($m_p$ – масса песка, $m_v$ – масса воды).

Ответ: 1,5 кг/л, или 1500 кг/м$^3$.

Задача 6. Смешали 1 кг воды плотностью 1000 кг/м$^3$ и 2 кг спирта плотностью 800 кг/м$^3$. Известно, что суммарный объем смеси составляет 95% от объема исходных компонент. Определите плотность получившейся смеси.

Тут прямо в условии нам показано, что $Vneq V_1+V_2$.

Плотность будет равна ($m_1$ – масса воды, $m_2$ – масса спирта).

Ответ: 902,25 кг/м$^3$.

Задача 7. В прямоугольном сосуде квадратного сечения (расстояние между стенками сосуда $a = 6$ см) плавает в вертикальном положении тонкостенный стакан квадратного сечения с толстым дном (длина внешней стороны квадрата $b = 4$ см). В пространство между стенками сосуда и стакана тонкой струйкой начинают наливать воду так, что за каждую секунду в сосуд поступает $mu = 2,7$ граммов. С какой скоростью $upsilon$ будет всплывать стакан? Плотность воды ρ=1000 кг/м$^3$.

Сколько воды поступит в стакан за время $Delta t$? $Delta m=mu Delta t$. Она растекается по стакану слоем толщины $h$. Для удобства можно представлять, что вся эта вода располагается у дна. Определим объем этой воды как $Delta V=h a^2$. С другой стороны,

Скорость подъема стакана равна

Задача 8. Однородная деталь из сплава с плотностью 2000 кг/м$^3$ имеет массу $m_1=54$ кг. А её точная копия, но в 3 раза меньших размеров, сделанная из сплава с плотностью 4000 кг/м$^3$, оказалась массой $m_2=2$ кг. Есть подозрение, что внутри копии существует скрытая полость. Какой у неё объём? Ответ дать в см$^3$.

Объем маленькой детали равен $V$, тогда, поскольку большая втрое больше, то ее объем больше в 27 раз – $27V$. Тогда плотность большой детали равна

Следовательно, ее объем равен

Плотность малой детали равна

Где $V_0$ – объем полости.

Задача 9. Для определения качества древесины были экспериментально определены массы досок различной длины. Их ширина равнялась 20 см, толщина 3 см. Зависимость массы досок m от их длины представлена в таблице. Постройте график этой зависимости и по нему найдите массу доски длиной 1 м и плотность древесины.

плотность

Строим график и по нему находим массу доски: 4,2 кг.

плотность

Для определения плотности возьмем точку не в начале графика, потому что чем больше значение, тем меньше относительная погрешность. Например, точку, где $m=9$ кг. Длина равна тогда (по графику) $L=2,1$. Тогда

Ответ: 4,2 кг, 714,3 кг/м$^3$.

Задача 10. Шарик накачали гелием. Масса газа составляет 20% от массы всего шарика. Через день, когда часть гелия просочилась через стенки, объем шарика уменьшился в 2 раза, а масса гелия стала составлять 10% от массы всего шарика. Определите, во сколько раз изменилась средняя плотность воздушного шарика.

Плотность шарика сначала:

Плотность после того, как он сдулся

Сначала масса складывалась из массы газа и массы оболочки:

После того, как шар сдулся, масса равна

Тогда, возвращаясь к плотностям, имеем:

Тогда отношение плотностей

Задача 11. В ящик с жесткими стенками, имеющий форму куба объемом 1 м в кубе и массой 300 кг, насыпали стальные шары диаметром 20 мм плотностью 7800 кг/м$^3$. Затем ящик потрясли и добавили в него столько шаров, что больше уже не получается засунуть ни одного шара (то есть получилась максимально плотная упаковка шаров в ящике). Суммарная масса шаров и ящика получилась 6072 кг. Далее в этот ящик с шарами досыпали еще мелких шариков диаметром 1 мм, сделанных из того же материала, и снова утрясли ящик до максимально возможного заполнения, досыпая при необходимости мелкие шарики. Оцените, какой после этого стала суммарная масса ящика с шарами и шариками.

Определяем массу шариков «крупного» размера:

Так как они заняли 1м$^3$, то средняя плотность упаковки $rho_=5772$ кг/м$^3$.

Поскольку плотность шариков известна, то определим их объем:

Тогда «свободного» пространства остается $V=1-0,74=0,26$ м$^3$.

Если плотность «упаковки» мелких шариков такая же, как и крупных, то их масса равна

Сложим плотности «крупных» и «мелких» шариков:

Задача 12. Большую коробку доверху заполнили деревянными кубиками, плотно уложив их ровными рядами. Через середины противоположных граней каждого из этих кубиков проделаны по три сквозных квадратных отверстия (схема одного кубика приведена на рисунке). Определите среднюю плотность содержимого коробки, если сторона кубика равна 9 см, а сторона отверстия 3 см. Плотность дерева 800 кг/м3 .

7_плотность_4

Определим, какую фигуру в итоге вырезали из каждого кубика. Она имеет форму пространственного креста:

плотность

Это заключение позволяют сделать размеры кубиков и размер отверстия. Этот «крест» будет состоять из 7 кубиков размером 3 на 3. То есть без отверстий кубик бы состоял из $3^3=27$ кубиков 3 на 3, а с отверстиями он лишился 7 кубиков, поэтому состоит из 20 кубиков 3 на 3. Определим массу 20 маленьких кубиков (то есть массу кубика с дырками):

Источник

Добавить комментарий