Вычисление средней плотности планеты (формула)
apd
Гуру
(2828),
закрыт
13 лет назад
Пожалуйста, подскажите формулу вычисления средней плотности планеты зная её радиус и массу. Плотность выразить в гр/см³ (грамм на кубический сантиметр)
Необходима именно формула! Заранее спасибо.
spin722
Мыслитель
(9200)
13 лет назад
Массу планеты разделить на объем планеты .
Объем планеты считаем как объем шара
4/3пи*R^3
Если значения массы подставить в формулу в граммах, а радиус планеты в сантиметрах – то плотность будет в граммах на сантиметр куб.
Условие задачи:
Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше, чем на экваторе. Период вращения планеты вокруг своей оси 2 ч 40 мин.
Задача №2.5.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(P_п=2P_э), (T=2; ч; 40; мин), (rho-?)
Решение задачи:
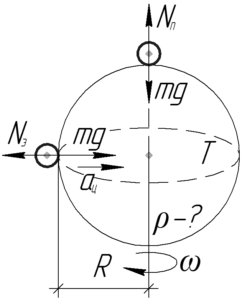 Тело на экваторе вращается вместе с планетой по окружности радиуса (R) (радиус планеты). Применим второй закон Ньютона:
Тело на экваторе вращается вместе с планетой по окружности радиуса (R) (радиус планеты). Применим второй закон Ньютона:
[mg – {N_э} = m{a_ц};;;;(1)]
Тело на полюсе лежит на оси вращения планеты, поэтому оно вращается лишь вокруг себя. Первый закон Ньютона для этого тела даст такое равенство:
[mg = {N_п};;;;(2)]
По третьему закону Ньютона сила реакции опоры ((N_э) и (N_п)) равна весу тела ((P_э) и (P_п) соответственно). Учтите, что эти силы хоть и равны по величине, но противоположны по направлению и приложены к разным телам. С учетом этого запишем равенства (1) и (2) в такой системе:
[left{ begin{gathered}
{P_э} = mg – m{a_ц} hfill \
{P_п} = mg hfill \
end{gathered} right.]
Поделим нижнее равенство на верхнее. Так как (P_п=2P_э), то получим:
[frac{g}{{g – {a_ц}}} = 2]
[2g – 2{a_ц} = g]
[g = 2{a_ц};;;;(3)]
Поскольку в задаче нужно узнать среднюю плотность планеты (rho), то запишем такие формулы: во-первых, формулу определения ускорения свободного падения (g) на поверхности планеты, во-вторых, формулу определения массы через плотность и объем, в-третьих, формулу определения объема шара.
[g = Gfrac{M}{{{R^2}}};;;;(4)]
[M = rho cdot V;;;;(5)]
[V = frac{4}{3}pi {R^3};;;;(6)]
Подставив (6) в (5), а полученное в (4), получим:
[g = frac{4}{3}pi Grho R;;;;(7)]
Чтобы выразить центростремительное ускорение (a_ц) через период вращения планеты (T) запишем такие формулы: формулу определения ускорения (a_ц) через угловую скорость (omega) и формулу связи последней с периодом вращения (T).
[{a_ц} = {omega ^2}R]
[omega = frac{{2pi }}{T}]
В итоге:
[{a_ц} = frac{{4{pi ^2}}}{{{T^2}}}R;;;;(8)]
Подставим выражения (7) и (8) в ранее полученное равенство (3):
[frac{4}{3}pi Grho R = frac{{8{pi ^2}}}{{{T^2}}}R]
[rho = frac{{6pi }}{{G{T^2}}}]
Переведем данный в условии период вращения (T) в систему СИ (в секунды):
[T = 2;ч;40;мин = 2 cdot 3600 + 40 cdot 60; с = 9600; с]
Посчитаем ответ:
[rho = frac{{6 cdot 3,14}}{{6,67 cdot {{10}^{ – 11}} cdot {{9600}^2}}} = 3065; кг/м^3 approx 3,07; г/см^3]
Ответ: 3,07 г/см3.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.5.14 Во сколько раз период обращения искусственного спутника, совершающего движение
2.5.16 На экваторе некоторой планеты тела весят вдвое меньше, чем на полюсе. Плотность
2.5.17 На экваторе некоторой планеты тела весят втрое меньше, чем на полюсе. Период
Ответ: Средняя плотность планеты Земля = 5482,9 кг/м³
Объяснение: Дано: R – радиус Земли = 6400км = 6400000 м
g – ускорение свободного падения = 9,8 м/с²
G – гравитационная постоянная = 6,67408 *10^-11 м³с^-2 кг^-1
Найти ρ -плотность планеты Земля
Среднюю плотность планеты Земля можно найти по формуле ρ = M/V. Здесь М – масса Земли; V – объем Земли. В первом приближении форму Земли можно считать шарообразной, тогда её объем можно найти по формуле V = 4*π*R³/3. Известно, что g определяется выражением: g = G*М/R². Из этого выражения М = g*R²/G. Подставив найденные выражения для массы и объема в формулу для нахождения плотности, будем иметь: ρ = 3*g*R²/4*G*π*R³ = 3*g/4*G*π*R = 3*9,8/4*6,67408 *10^-11*3,14*6400000 = 5482,9 кг/м³
Плотность планеты
Плотность — это физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму.
Плотность планеты Земля = 5500 кг/м3.
Рассчитать плотность можно с помощью этой онлайн программы плотности (если известна масса и объем).
Любые данные по плотности важны в научных и практических работах.
— выполнение прикладных расчетов
— оценка влияния плотности на объект исследования
В проектной деятельности любое решение должно подтверждаться научно подтвержденными данными.
Использование данных по плотности целесообразно для выполнения прикладного расчета или задачи.
На этой странице представлена основная простейшая информация о плотности. Точное значение плотности зависит от температуры и давления. В нашей проектной организации вы можете заказать расчет плотности для любого материала.
Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше
Определить плотность шарообразной планеты, если вес тела на полюсе в 2 раза больше, чем на экваторе. Период вращения планеты вокруг своей оси 2 ч 40 мин.
Задача №2.5.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
 Тело на экваторе вращается вместе с планетой по окружности радиуса (R) (радиус планеты). Применим второй закон Ньютона:
Тело на экваторе вращается вместе с планетой по окружности радиуса (R) (радиус планеты). Применим второй закон Ньютона:
Тело на полюсе лежит на оси вращения планеты, поэтому оно вращается лишь вокруг себя. Первый закон Ньютона для этого тела даст такое равенство:
По третьему закону Ньютона сила реакции опоры ((N_э) и (N_п)) равна весу тела ((P_э) и (P_п) соответственно). Учтите, что эти силы хоть и равны по величине, но противоположны по направлению и приложены к разным телам. С учетом этого запишем равенства (1) и (2) в такой системе:
Поделим нижнее равенство на верхнее. Так как (P_п=2P_э), то получим:
Поскольку в задаче нужно узнать среднюю плотность планеты (rho), то запишем такие формулы: во-первых, формулу определения ускорения свободного падения (g) на поверхности планеты, во-вторых, формулу определения массы через плотность и объем, в-третьих, формулу определения объема шара.
Подставив (6) в (5), а полученное в (4), получим:
Чтобы выразить центростремительное ускорение (a_ц) через период вращения планеты (T) запишем такие формулы: формулу определения ускорения (a_ц) через угловую скорость (omega) и формулу связи последней с периодом вращения (T).
Подставим выражения (7) и (8) в ранее полученное равенство (3):
Переведем данный в условии период вращения (T) в систему СИ (в секунды):
[T = 2;ч;40;мин = 2 cdot 3600 + 40 cdot 60; с = 9600; с]
Ответ: 3,07 г/см 3 .
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
О массах и плотностях планет

Планеты Солнечной системы. Авторы и права: CC0 Public Domain.
То, что планеты Солнечной системы значительно различаются по своему размеру, является хорошо известным фактом.
Так, например, планеты внутренней части нашей системы имеют меньшие размеры, но являются более плотными, чем газовые или ледяные гиганты, располагающиеся во внешней части Солнечной системы. А в ряде случаев, планеты могут быть даже меньше, чем некоторые спутники. Однако размер планеты не обязательно пропорционален его массе.
Спасибо за интерес к сайту!
Вы можете поддержать проект “Вселенная Сегодня” удобным для вас способом:
5599 0020 1641 0583
9112 3930 4027 6490
Z215342785781
Таким образом, в то время как Меркурий может быть меньше по размеру, чем спутник Юпитера Ганимед или спутник Сатурна Титан, он более чем в два раза массивнее этих спутников. И в то время как Юпитер в 318 раз массивнее Земли, его радиус лишь в 11,21 раза больше земного.
Давайте пройдёмся по каждой из планет и посмотрим, насколько они различаются.
Меркурий
Со средним диаметром 4879 километров (3031,67 миль) Меркурий является самой маленькой планетой Солнечной системы. Он также является второй (после Земли) по плотности планетой: 5,427 г/см 3 .
Меркурий, как и другие планеты земной группы состоит из силикатных пород и минералов, а также железного ядра, которое в отличии от других планет является аномально большим по отношению к коре и мантии. Таким образом масса Меркурия составляет около 0,330*10 24 кг., что эквивалентно 0,055 массы Земли. Сила меркурианского притяжения составляет всего 3,7 м/с 2 .

Меркурий. Авторы и права: NASA / Johns Hopkins University Applied Physics Laboratory / Carnegie Institution of Washington.
Венера
Венера, которая из-за сходства состава, размера и массы порой часто именуется “сестрой Земли” имеет плотность 5,243 г/см 3 . Она является второй планетой от Солнца, а её средний радиус составляет примерно 6050 километров (3759,3 миль). Таким образом масса планеты достигает 4,87*10 24 кг., что эквивалентно 0,815 массы Земли. Учитывая плотность и размеры, сила тяжести на Венере сопоставима с Земной и равна примерно 8,87 м/с 2 .

Венера в реальных цветах. Фото получено зондом Mariner. Исходные изображения находятся в общественном достоянии. Авторы и права: NASA / Ricardo Nunes.
Земля
Как и другие планеты внутренней части Солнечной системы, Земля также состоит из металлов и силикатов. Со средним радиусом 6371 километров (3 958 миль) и средней плотностью 5,514 г/м 3 , она является наиболее крупной и самой плотной, из планет земной группы. Масса Земли достигает 5,97*10 24 кг., а сила земного притяжения, как все вы знаете равна 9,8 м/с 2 .
Марс является третьей по величине планетой земной группы. Как и другие, Марс состоит из металлов и силикатных пород, но в то время как он примерно в два раза меньше Земли (со средним диаметром 6792 километров, или 4220 миль), его масса составляет всего одну десятую массы Земли.
Короче говоря, Марс имеет массу 0,642*10 24 кг., или примерно 0,11 массы Земли. Учитывая размеры и плотность (составляющую 3,9335 г/см 3 ) сила притяжения на Марсе не превышает 3,8 м/с 2 .

Марсоход “Curiosity” получил этот автопортрет 23 января 2018 года, когда он находился на склонах горы Шарп. Авторы и права: NASA JPL-Caltech.
Юпитер
Юпитер является самой крупной планетой в Солнечной системе. Учитывая то, что его средний диаметр равен 142984 километров, в нём могут поместиться все другие планеты нашей системы (кроме Сатурна). Однако с массой 1898*10 24 кг., Юпитер почти в 2,5 раза массивнее всех других планет в Солнечной системе вместе взятых. Тем не менее, как газовый гигант, он имеет более низкую общую плотность, чем планеты земной группы. Его средняя плотность равна 1,326 г/см 3 .
Сатурн
Сатурн является вторым по величине газовым гигантом; и со средним диаметром 120536 километров, он всего лишь немного меньше, чем Юпитер. Тем не менее, он значительно менее массивен, чем его двоюродный брат Юпитер. С массой 569*10 24 кг. Сатурн в 95 раз массивнее Земли, однако его плотность составляет всего 0,687 г/см 3 . Сатурн является единственной планетой в Солнечной системе, которая имеет меньшую плотность, чем вода (1 г/см 3 ).

Облака Сатурна. Авторы и права: NASA / Cassini.
Средний диаметр Урана равен 120536 километров, он является третьей по величине планетой в Солнечной системе. С массой 86,8*10 24 кг., Уран – это четвёртая наиболее массивная планета. Средняя плотность, таким образом, достигает 1,271 г/см 3 .
Нептун
Нептун примерно в четыре раза больше Земли (диаметр 49528 километров), а его масса равна 102*10 24 кг. Таким образом плотность Нептуна больше, чем плотность любого из газовых гигантов (1,638 г/см 3 ).
Исходя из вышесказанного, вы можете увидеть, что массы планет Солнечной системы значительно варьируются. Но если мы говорим о плотности, то она не всегда пропорциональна размерам. Короче говоря, в то время как некоторые планеты могут быть всего в несколько раз больше, чем другие, они при этом могут быть во много и много раз более массивными.
Понравилось? Расскажи друзьям:

Вы могли пропустить:

Встречайте китайский марсоход “Чжуронг”

Астрономы наблюдают необычные затемнения молодой звезды

Вселенная может быть на 1,2 миллиарда лет моложе
Комментарии 4
Интересная получается ситуация: астрономы размеры скалистых планет (Марса, Земли, Венеры и Меркурия), а также спутников Юпитера и Сатурна измеряют по поверхности твёрдой агрегатной фазы вещества, игнорируя, не учитывая протяжённость атмосферы таких планет и спутников больших планет газовых гигантов.
Но размеры планет газовых гигантов измеряют по границы внешних облаков в их атмосферах. И размеры звёзд, в частности Солнца, измеряют по видимой внешней границе их фотосфер-атмосфер.
Автор публикации ошибся с обозначением диаметра Сатурна и Урана: привёл абсолютно одинаковую величину 120536 км.
Мне интересна общая шкала массы и средней плотности вещества планет (и относительно крупных спутников планет) и звёзд.
Потому что в моей модели вселенной объём пространства неплотной материи вакуума и эфира космоса и масса плотной материи вещества равно пропорционально расту на Объёмно-массовую Постоянную хаббла: 6,9*10^-18 в секунду, то есть, удваиваются за период времени около 3,173 миллиардов лет.
Исключена гипотеза Большого Взрыва.. Вселенная всегда была и всегда будет существовать, мульти локально прирастая объёмом пространства неплотной материей вакуума, электростатики и магнетизма эфира микроскопическими большими взрывами.из каждого нейтрона, протона, ядра атома и электрона. И половина от прирастающего объёма пространства космоса порциями по 4-5,5 кубических метров самофокусируются и сжимаются в объёмы пространства по 10^-47 — 10^-46 кубических метров плотной материи новых атомных единиц массы в форме новых нейтронов.
Это значит, что астероиды могут вырастать в скалистые планеты , которые вырастают в планеты газовые гиганты, которые вырастают в звёзды коричневые карлики и т.д.
Естественно какие-то космические объекты сталкиваются и раскалываются на осколки, а также сливаясь в один объект. Газово-пылевые облака, наверное могут фрагментироваться и сжиматься в какие-то космические объекты. Но больше вероятность, что рассеиваются и постепенно конденсируются на затравочные камни, льдинки и так намораживаются в кометы с их веществом из льда и вмороженной пыли.
Никогда не осуществлялся приказ на сотворение вселенной отданный в 1927 году аббатом Жоржем Леметром на совершения 14 миллиардов лет назад одного-единственного супер большого Большого Взрыва рождения из ничего сразу всей массы вещества и всей энергии и некоторого первичного объёма пространства вакуума и эфира космоса вселенной.
Просто потому что вселенная всегда была и всегда будет существовать. Ведь вселенная самодостаточна работой процесса своего бытия с коэффициентом полезного действия 1,0000000000000000069 в секунду, который можно назвать Объёмно-Массовой Постоянной Хаббла.
Доказательством этого является достоверно наблюдаемый астрономами рост объёма пространства. Это отражают Линейной Постоянной Хаббла: 2,3*10-18 в секунду, то есть 1,0000000000000000023 в секунду.
Вероятно, в грамме любого вещества рождается около 4,155 миллионов новых нейтронов в секунду. Почти все эти нейтроны в относительно холодном веществе включаются в состав ядер атомов разных изотопов разных элементов…
Сравнительная диаграмма масс планет Солнечной системы. Масса Юпитера составляет 71 %, а масса Сатурна 21 % от суммарной массы всех планет. Масса планет земной группы весьма незначительна, у Меркурия она составляет всего 0,1 %, что в данном масштабе не видно.
Астрофизика — раздел астрономии, изучающий небесные тела, их системы и пространство между ними на основе анализа происходящих во Вселенной физических процессов и явлений.
Объекты изучения астрофизики:
- космические тела от космических пылинок до межгалактических структур и Вселенной в целом;
- различные виды полей (гравитационные, магнитные, электромагнитные);
- геометрические свойства космического пространства.
Цель астрофизики — установление закономерности и понимание строения, взаимодействия и эволюции небесных тел, их систем и Вселенной как целого.
Диапазон физических параметров – плотности, температуры, давления, напряженности магнитного поля, с которыми приходится иметь дело в астрофизике — во много раз превосходит достижимый в лабораториях на Земле. Поэтому многие астрофизические объекты выступают в роли уникальной физической лаборатории, которая дает возможность изучать вещества и поля в экстремальных условиях. Это делает астрофизику неотъемлемой частью физики.
В зависимости от объекта изучения выделяются следующие разделы астрофизики:
- физика Солнечной системы (гелиофизика);
- физика звезд и межзвездной среды;
- физика галактическая (изучение Млечного Пути);
- внегалактическая астрономия (изучение объектов за пределами Млечного Пути);
- космология (изучение Вселенной в целом).
Различают также радиоастрономию, рентгеновскую, инфракрасную и ультрафиолетовую астрономию, субмиллиметровую и гамма-астрономию. Эти подразделы различаются спектральным диапазоном, в котором ведутся наблюдения за космическими телами и процессами.
Физика звезд
Физика звезд является одним из главных разделов астрофизики. Она изучает строение наружных слоев звезды, внутренне содержимое этих тел, а также происходящие внутри процессы, которые определяет строение и эволюцию звезд.
Звезда — массивное самосветящееся небесное тело, состоящее из газа или плазмы, в котором происходят, происходили или будут происходить термоядерные реакции.

Один из методов исследования звезд является изучение звездного спектра, на основании анализа которого ученые смогли установить химический состав этих тел. Установлено, что атмосфера большинства звезд напоминает атмосферу Солнца, в состав которой входит:
- 70% водорода;
- 27% гелия;
- до 3% — другие элементы, в том числе тяжелые.
В астрофизике звезды классифицируют по различным параметрам: по температуре, по размерам и массам.
Спектральная классификация звезд
Согласно спектральной классификации спектральный класс звезд определяется поверхностной температурой звезды и обозначается определенной буквой (O; B; A; F; G; K; M) — именно в такой последовательности. Класс O — самый высокий класс в иерархии, а класс MM – самый низкий. Чем выше класс, иерархии, тем звезды горячее, больше, ярче. А чем ниже класс, тем, соответственно они холоднее, меньше, тусклее, но такие звезды живут дольше, чем звезды выше классом.
Совет! Чтобы запомнить последовательность спектральных классов звезд, запомните следующую фразу: «Один Высокий Англичанин Финики Жевал Как Морковь». Первые буквы слов в ней идут в такой же последовательности, как и классы звезд.

Цвет звезды также определяется ее температурой (в скобках — наименование класса и температура поверхности звезды в Кельвинах):
- голубые звезды (О, 30 000 – 60 000);
- бело-голубые звезды (В, 10 000 – 30 000);
- белые звезды (А, 7500 – 10 000);
- желто-белые звезды (F, 6000 – 7000);
- желтые звезды (G, 5000 – 6000);
- оранжевые звезды (К, 3500 – 5000);
- красные звезды (М, 2000 – 3500);
- коричневые звезды (нет класса, 900–2700).
Солнце имеет класс G, так как его поверхность имеет температуру 5800–5900 К. Это желтая звезда, являющаяся центром Солнечной системы. Внутри Солнце очень горячее. В центральной точке температура может достигать 15 млн К.
Классификация по размерам
Звезды по размерам делятся на 4-и типа:
- Обычные звезды (средние). Они соизмеримы с Солнцем.
- Карлики. Меньше Солнца в сотни раз.
- Гиганты. Больше Солнца в десятки раз.
- Сверхгиганты. Больше Солнца в сотни раз.
Внимание! Несмотря на то, что эта классификация звезд по размерам, при сравнении нужно учитывать массы звезд. Так, обычными звездами считаются те, масса которых сравнима с массой Солнца.
Пример №1. Ниже дана таблица с названиями некоторых звезд, их температурой, массой, радиусом и расстоянием до них. Среди них выделите звезды — голубые гиганты.
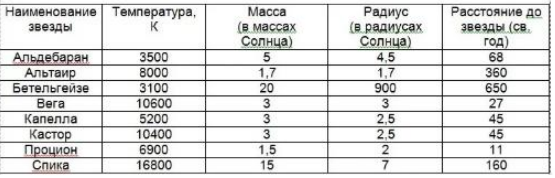
Голубой свет излучают звезды с температурой от 10 до 30 тыс. К. Из таблицы голубыми являются звезды: Вега, Кастор и Спика. Звезда-гигант должна быть в десятки раз больше Солнца. Чтобы сравнить величину звезд, нужно сравнить их массы. Вега и Кастор весят лишь в 3 раза больше Солнца, в то время как Спика — в 15 раз. Поэтому голубой гигант здесь — только Спика.
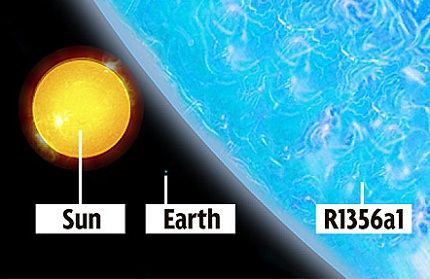
Это интересно! Самая большая из известных звезд — R136a1 — была обнаружена в Большом Магелланом Облаке в 2010 году. Она больше Солнца в 256 раз.
Классификация звезд на основе диаграммы Герцшпрунга – Расселла
Среди астрономов также применяется классификация, основанная на диаграмме Герцшпрунга – Расселла. На этой диаграмме по оси абсцисс откладываются спектральные классы (или эффективные температуры), по оси ординат — светимости L (или абсолютные звездные величины M). Если бы между светимостями и их температурами не было никакой зависимости, то все звезды распределялись на такой диаграмме равномерно. Но на диаграмме обнаруживаются несколько закономерностей, которые называют последовательностями.
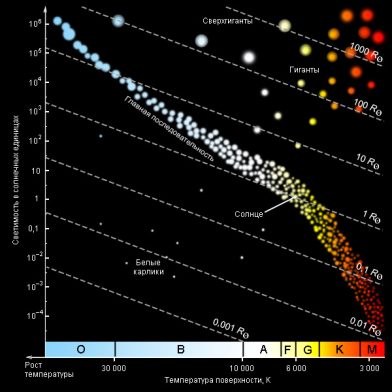
Большинство звезд (около 90 %), располагаются на диаграмме вдоль длинной узкой полосы, называемой главной последовательностью. Она протянулась из верхнего левого угла (от голубых сверхгигантов) в нижний правый угол (до красных карликов). К звездам главной последовательности относится Солнце, светимость которого принимают за единицу.
Точки, соответствующие гигантам и сверхгигантам, располагаются над главной последовательностью справа, а соответствующие белым карликам – в нижнем левом углу, под главной последовательностью.
По распределению звезд в соответствии с их светимостью и температурой на диаграмме Герцшпрунга–Рассела выделены следующие классы светимости:
- сверхгиганты – I класс светимости;
- гиганты – II класс светимости;
- звезды главной последовательности – V класс светимости;
- субкарлики – VI класс светимости;
- белые карлики – VII класс светимости.
Внимание! Принято указывать класс светимости после спектрального класса звезды. Солнце – звезда G2V.
В настоящее время выяснилось, что звезды главной последовательности – нормальные звезды, похожие на Солнце, в которых происходит сгорание водорода в термоядерных реакциях. Главная последовательность – это последовательность звезд разной массы. Самые большие по массе звезды располагаются в верхней части главной последовательности и являются голубыми гигантами. Самые маленькие по массе звезды – карлики. Они располагаются в нижней части главной последовательности. Параллельно главной последовательности, но несколько ниже ее располагаются субкарлики. Они отличаются от звезд главной последовательности меньшим содержанием металлов.
Происхождение и эволюция звезд
Звезды возникали в ходе эволюции галактик. Большинство астрономов считают, что это происходило в результате сгущения (конденсации) облаков материи, которые постепенно формировались внутри галактик.
Этапы эволюции звезд:
- Стадия образования протозвезды — образуется шарообразное тело в холодном газопылевом облаке в результате действия сил тяготения.
- Стадия сжатия звезд — протозвезда сжимается и становится более плотной. Образуется молодая звезда.
- Стационарная стадия — начало термоядерных реакций. Из водорода образуется гелий, формируя гелиевое ядро. В ядре из гелия образуются более тяжелые элементы.
- Заключительная стадия (зависит от массы звезды).
Внешние слои звезд, подобных нашему Солнцу (но с массами, не большими 1,2 массы Солнца), постепенно расширяются и, в конце концов, совсем покидают ядро звезды. На месте гиганта остается маленький и горячий белый карлик. Белых карликов в мире звезд много. Это значит, что многие звезды превращаются в белых карликов, которые затем постепенно остывают, становясь «потухшими звездами».
Более массивные звезды могут потерять устойчивость и взорваться с образованием сверхновой звезды, которая обогащает космос новыми химическими элементами. Впоследствии она сжимается и образует нейтронную звезду. Если масса звезды превышает массу Солнца в 2 и более раз, то при взрыве сверхновой может произойти коллапс с образованием черной дыры.
Сверхновая звезда (супернова) — физическое явление, при котором происходил взрыв звезды.

Нейтронная звезда — звезда, состоящая, в основном, из нейтронной сердцевины, покрытой сравнительно тонкой корой вещества в виде тяжёлых атомных ядер и электронов. Радиус нейтронных звезд не превышает 10–20 км. При этом их масса сравнима с массой Солнца или превышает ее в 8–10 раз.

Черная дыра — это объект с колоссальной массой и плотностью, гравитация которого настолько сильная, что не позволяет его покинуть даже световым квантам. Наиболее массивные черные дыра располагаются в центре галактик.

Солнечная система
Солнечная система — планетная система, включающая в себя центральную звезду — Солнце — и все естественные космические объекты, обращающиеся вокруг Солнца. Между всеми небесными телами во Вселенной существуют силы взаимного притяжения. Этими силами Солнце удерживает возле себя планеты и другие небесные тела.
Всего в Солнечной системе 8 планет:
- Меркурий,
- Венера,
- Земля,
- Марс,
- Юпитер,
- Сатурн,
- Уран,
- Нептун,
- Плутон (не является планетой с 2006 года).
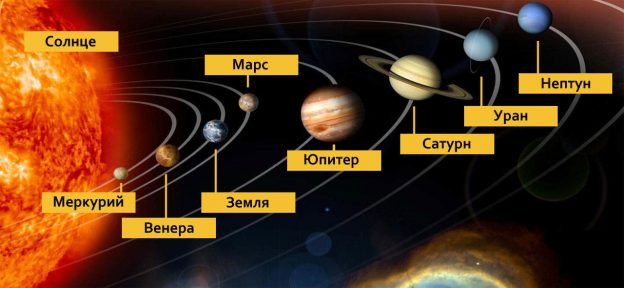
Внимание! Самая большая планета Солнечной системы — Юпитер.
Все планеты Солнечной системы делятся на 2 группы:
- Земного типа (Меркурий, Венера, Земля, Марс).
- Газовые гиганты (Юпитер, Сатурн, Уран и Нептун).
Между Марсом и Юпитером находится пояс астероидов — относительно небольших небесных тел Солнечной системы, движущихся по орбите вокруг Солнца. Последние исследования обнаружили еще один пояс астероидов за Нептуном (пояс Койпера). Плутон сравним по размеру с астероидами. Именно поэтому его перестали считать планетой.
Почти все планеты имеют спутники. Их нет только у Венеры и Меркурия. У Земли спутник один — это Луна. Чем больше масса, а соответственно и гравитация планеты, тем больше у нее спутников. Больше сего спутников у Юпитера. По последним данным их не менее 79. Самые известные из них (расположены в порядке удаленности): Ио, Европа, Ганимед и Каллисто. Сатурн имеет так называемое кольцо, которое содержит множество объектов являющимися спутниками. Кольца есть у всех газовых гигантов Солнечной системы, но у Сатурна оно самое большое и выраженное.

Внимание! Все планеты, кроме Меркурия, имеют атмосферу — газовую оболочку небесного тела, удерживаемую около него гравитацией.
Все планеты вращаются по эллиптическим орбитам. Один оборот Земля делает за сутки, одно вращение вокруг Солнца — за год. Смену времен года на Земле определяет ее наклон оси к плоскости вращения, которая называется эклиптикой.
Основные формулы:
| Наименование искомой величины | Формула | Обозначения |
| Объем планеты (любого другого шарообразного тела) | V=43πR3 | π — число «пи» (округленно 3,14)
V — объем планеты (тела); R — радиус планеты (тела). |
| Масса планеты (тела) | M=ρV | M — масса;
ρ — среднее значение плотности; V — объем планеты (тела). |
| Ускорение свободного падения планеты (тела) | g=GMR2 | g — ускорение свободного падения (на Земле 9,8 м/с2);
G — гравитационная постоянная (6,67∙10–11 м3/(кг∙ с2)); M — масса; R — радиус планеты (тела). |
| Первая космическая скорость (минимальная горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты) | v1=√gR | v1 — первая космическая скорость;
g — ускорение свободного падения; R — радиус планеты (тела). |
| Вторая космическая скорость (наименьшая скорость, которую необходимо придать стартующему с поверхности небесного тела объекту, масса которого пренебрежимо мала по сравнению с массой небесного тела, для преодоления гравитационного притяжения и покидания замкнутой орбиты вокруг него) | v2=v1√2 | v1 — первая космическая скорость;
v2 — вторая космическая скорость. |
| Сила гравитационного притяжения между двумя телами | F=GM1M2R2 | F — сила гравитационного притяжения тел 1 и 2;
M1 — масса первого тела; M2 — масса второго тела; G — гравитационная постоянная; R — радиус планеты (тела). |
Пример №2. Определить вторую космическую скорость Марса.
v2=v1√2=√2gR
Ускорение свободного падения:
g=GMR2
Тогда:
v2=√2GMR2R=√2GMR
Радиус Марса — 3,4∙106 м. Масса Марса — 6,4∙1023 кг.
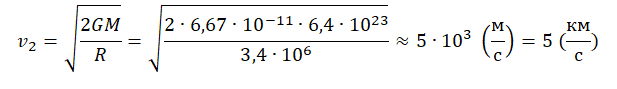
Задание EF19040
Внимательно прочитайте текст задания и выберите верный ответ из списка.
Рассмотрите таблицу, содержащую сведения о ярких звёздах.
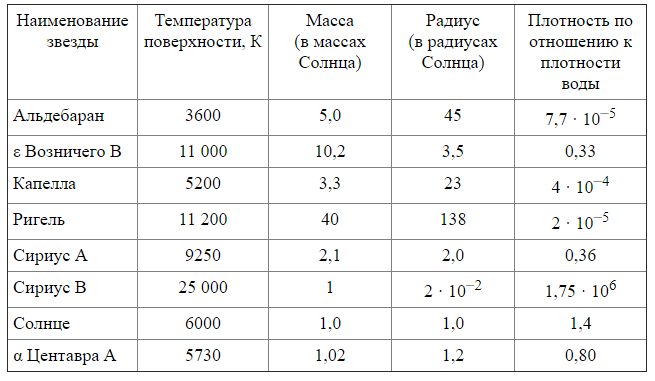
Выберите два утверждения, которые соответствуют характеристикам звёзд.
Ответ:
А) Наше Солнце имеет максимальную массу для звёзд главной последовательности на диаграмме Герцшпрунга – Рессела.
Б) Звезда Ригель относится к сверхгигантам.
В) Звезда Сириус А относится к звёздам главной последовательности на диаграмме Герцшпрунга – Рессела.
Г) Звезда α Центавра А относится к белым карликам.
Д) Звезда Сириус В относится к звёздам главной последовательности на диаграмме Герцшпрунга – Рессела.
Алгоритм решения
- Проанализировать каждое из утверждений и установить, верные ли они.
- Выбрать только верные утверждения.
Решение
Согласно утверждению А, наше Солнце имеет максимальную массу для звёзд главной последовательности на диаграмме Герцшпрунга – Рессела. Но это не так, потому что главная последовательность включает в себя звезды различных масс. И Солнце не является в ней самой массивной звездой. Утверждение А — неверное.
Согласно утверждению Б, звезда Ригель относится к сверхгигантам. Это так, потому что к сверхгигантам относят те звезды, масса которых больше массы Солнца в десятки и более раз. Утверждение Б — верное.
Согласно утверждению В, звезда Сириус А относится к звёздам главной последовательности на диаграмме Герцшпрунга – Рессела. Это действительно так. Утверждение В — верное.
Согласно утверждению Г, звезда α Центавра А относится к белым карликам. Но это не так. Белые звезды имеют температуру выше 7500 К и массу меньше солнечной в 100 и более раз. Утверждение Г — неверное.
Согласно утверждению Д, звезда Сириус В относится к звёздам главной последовательности на диаграмме Герцшпрунга – Рессела. Это не так. Эта звезда относится к бело-голубым карликам, которая лежит ниже главной последовательности. Утверждение Д — неверное.
Ответ: БВ
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22793
Внимательно прочитайте текст задания и выберите верный ответ из списка
На рисунке представлена диаграмма Герцшпрунга – Рессела.
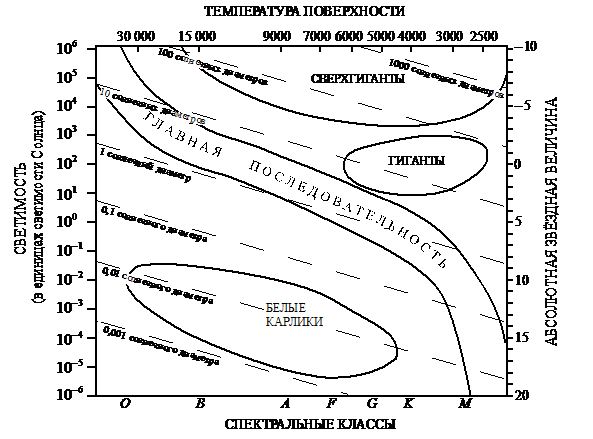
Выберите два утверждения о звёздах, которые соответствуют диаграмме.
Ответ:
А) Температура поверхности звёзд спектрального класса G выше температуры поверхности звёзд спектрального класса А.
Б) Радиус звезды Бетельгейзе почти в 1000 раз превышает радиус Солнца, а значит она относится к сверхгигантам.
В) Плотность белых карликов существенно меньше средней плотности гигантов.
Г) Звезда Антарес имеет температуру поверхности 3300 К и относится к звёздам спектрального класса А.
Д) «Жизненный цикл» звезды спектрального класса K главной последовательности более длительный, чем звезды спектрального
класса В главной последовательности.
Алгоритм решения
- Проанализировать каждое из утверждений и установить, верные ли они.
- Выбрать только верные утверждения.
Решение
Согласно утверждению А, температура поверхности звёзд спектрального класса G выше температуры поверхности звёзд спектрального класса А. Но это не так, потому что спектральные классы звезд располагаются на оси от большей температуры к меньшей. Утверждение А — неверное.
Согласно утверждению Б, радиус звезды Бетельгейзе почти в 1000 раз превышает радиус Солнца, а значит она относится к сверхгигантам. Это действительно так. Утверждение Б — верное.
Согласно утверждению В, плотность белых карликов существенно меньше средней плотности гигантов. Нет, гиганты имеют меньшую плотность. Утверждение В — неверное.
Согласно утверждению Г, звезда Антарес имеет температуру поверхности 3300 К и относится к звёздам спектрального класса А. Но это не так. К классу А относятся звезды с температурой выше 7500 К. Утверждение Г — неверное.
Согласно утверждению Д, «Жизненный цикл» звезды спектрального класса K главной последовательности более длительный, чем звезды спектрального класса В главной последовательности. Это действительно так. Такие звезды медленнее расходуют свое топливо, а потому дольше живут. Утверждение Д — верное.
Ответ: БД
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22761
Внимательно прочитайте текст задания и выберите верный ответ из списка
Рассмотрите таблицу, содержащую характеристики планет Солнечной системы.
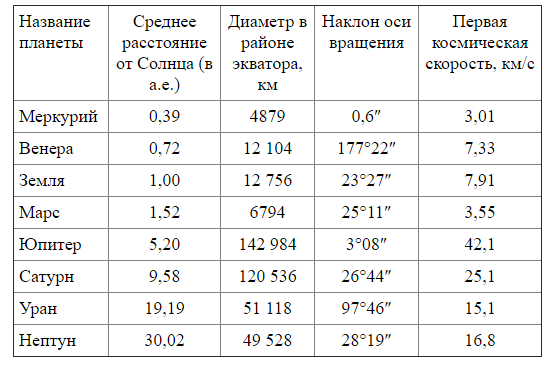
Выберите два утверждения, которые соответствуют характеристикам планет.
Ответ:
А) Чем дальше планета от Солнца, тем больше первая космическая скорость для её спутников.
Б) Ускорение свободного падения на Сатурне составляет около 10,5 м/с2.
В) Вторая космическая скорость при старте с поверхности Юпитера составляет 25 км/с.
Г) Среднее расстояние от Венеры до Солнца в три раза меньше, чем от Марса до Солнца.
Д) На Марсе может наблюдаться смена времён года.
Алгоритм решения
1.Проанализировать каждое из утверждений и установить, верные ли они.
2.Выбрать только верные утверждения.
Решение
Согласно утверждению А, чем дальше планета от Солнца, тем больше первая космическая скорость для её спутников. Но это не так, потому что первая космическая скорость зависит только от радиуса планеты и ускорения свободного падения:
v1=√gR
Утверждение А — неверное.
Согласно утверждению Б, ускорение свободного падения на Сатурне составляет около 10,5 м/с2. Это действительно так, что можно подтвердить вычислениями:
g=GMR2
Радиус Сатурна равен около 60,25∙106 м (половина диаметра, взятого из таблицы), а его масса равна около 5,7∙1026 кг (табличная величина).
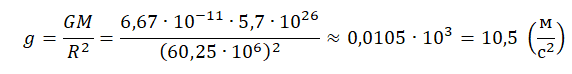
Утверждение Б — верное.
Согласно утверждению В, вторая космическая скорость при старте с поверхности Юпитера составляет 25 км/с. Нет, это неправильно. Вторая космическая скорость определяется формулой:
v2=v1√2
В таблице первая космическая скорость для Юпитера составляет 42,1 км/ч. Поэтому вторая космическая скорость никак не может быть меньше первой. Утверждение В — неверное.
Согласно утверждению Г, среднее расстояние от Венеры до Солнца в три раза меньше, чем от Марса до Солнца. Но это не так — согласно данным из таблицы, среднее расстояние от Венеры до Солнца составляет 0,72 а.е., а от Марса до Солнца — 1,52 а.е. Утверждение Г — неверное.
Согласно утверждению Д, на Марсе может наблюдаться смена времён года. Это действительно так. Угол наклона оси вращения составляет чуть более 25 градусов, что на 2 градуса, больше чем на Земле, на которой смена времен года ярко выражена по обеим сторонам от экватора. Утверждение Д — верное.
Ответ: БД
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 2.7k
