Приборы
и принадлежности:
весы, набор
разновесок, скамеечка к весам, исследуемое
твёрдое тело, исследуемая жидкость,
дистиллированная вода, проволочка для
подвешивания тела к коромыслу весов,
стеклянный стаканчик- 2 шт.
Цель
работы:
-
Определить
плотность твёрдого тела. -
Определить
плотность жидкости.
ХОД
РАБОТЫ:
-
Составим таблицу
для внесения в неё значений полученных
величин.
Температура
окружающего воздуха равна 22° C.
Таблица 1.
|
m, |
m1, |
, |
m2, |
m |
|
|
37,1 |
32,4 |
7,878 |
33,2 |
3,9 |
0,828 |
-

При помощи тонкой проволочки
(рис. 1) подвесим исследуемое тело (А) к
левому коромыслу весов, уравновесим
гирями и определим m1
– массу тела вместе с
проволокой. Подвешивание
Подвешивание
тела произведём с таким расчётом, чтобы
после того, как над чашкой весов будет
установлена скамеечка со стаканом
жидкости, тело не касалось дна и стенок
стакана. Тело и проволочка при этом
должны быть сухими и чистыми.
-
Установим
над чашкой весов скамеечку (В), поставим
на неё стакан и нальём дистиллированную
воду до такого уровня, чтобы тело при
качаниях коромысла весов оставалось
полностью погруженным в воду, а проволочка
была погружена на глубину около 1 см.
Приведём
весы в равновесие и определим m1
– массу
гирь, уравновешивающих вес тела с
проволочкой, погруженных в воду, плотность
которой при данной температуре обозначим
ж.
-
По
данным таблицы вычислим плотность
исследуемого твёрдого тела:
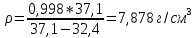 .
.
Исходя
из полученного значения плотности
вещества и температуры окружающей среды
можно сделать вывод, что исследуемое
тело изготовлено из стали.
-
Заменив
стакан с дистиллированной водой стаканом
с исследуемой жидкостью, прежним
способом погрузим в него тело, которое
использовалось в предыдущем задании,
предварительно осушив его и проволочку
фильтровальной бумагой. -
Уравновесим
весы и определим таким же способом
массу гирь m2
для исследуемой жидкости. Результаты
измерений занесём в таблицу 1. -
определим
плотность жидкости:
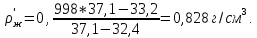
Исходя из полученного
значения плотности вещества и температуры
окружающей среды можно сделать вывод,
что исследуемое вещество керосин.
ОБРАБОТКА
РЕЗУЛЬТАТОВ:
В
настоящей работе каждое измерение
проводится по одному разу, поэтому
определение случайных погрешностей
теряет смысл. Здесь можно оценить лишь
систематическую погрешность, связанную
с точностью приборов.
Величина
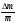
определяется классом точности весов.
Чувствительность лабораторных весов
составляет порядка 10 мг, поэтому
абсолютная погрешность определения
массы имеет тот же порядок.
Оценим
погрешность определения плотности:
 .
.
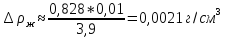 .
.
ВЫВОД:
В
данной лабораторной работе мы
экспериментальным путём определили
плотность твёрдого тела и жидкости
методом гидростатического взвешивания
и материала, из которого они состоят.
Полученные результаты по точности
измерений удовлетворяют требованиям.
КОНТРОЛЬНЫЕ
ВОПРОСЫ
-
Докажите закон
Архимеда.
Заменим мысленно
погруженное в жидкость тело этой же
жидкостью, которая отвердела, сохранив
свою плотность. На это тело будет
действовать такая же сила Архимеда, что
и на данное тело: ведь его поверхность
совпадает с поверхностью выделенного
объема жидкости, а силы давления на
различные участки поверхности остались
такими же.
Выделенный объем
жидкости, «плавая» внутри той же жидкости,
находится в равновесии. Значит, действующие
на него сила тяжести Fт
и сила Архимеда FA
уравновешивают друг друга, то есть равны
по модулю и направлены противоположно.
Для покоящегося тела сила тяжести равна
весу — значит, сила Архимеда равна весу
выделенного объема жидкости. А это и
есть объем погруженной части тела.
-
Можно ли методом
гидростатического взвешивания определить
плотность дерева? Почему? Что получится
в результате такого измерения?
Плотность дерева
можно определить способом гидростатического
взвешивания, при условии, что плотность
используемой жидкости меньше плотности
исследуемого тела.
|
Дерево |
pд, |
Жидкость |
pж, |
|
|
Хурма |
1,08 |
Ацетон |
0,792 |
|
|
Квебрахо |
1,21 |
Бензин |
0,68-0,72 |
|
|
Гваякум |
1,28 |
Пентан |
0,626 |
|
|
Железное |
1,35 |
Нефть |
0,55-1,05 |
|
|
Жидкий |
0,07 |
-
Плотность железа
приблизительно в 8 раз больше плотности
воды. Почему же корабли, корпуса которых
изготовлены из стали, не тонут?
Корабля, изготовленные
из сталей и другим материалов, чья
плотность больше плотности воды не
тонут потому, что сила тяжести,
воздействующая на воду со стороны
корабля, уравновешивается с выталкивающей
силой, воздействующей на корабль со
стороны воды. Для удержания корабля на
плаву необходимо, чтобы объём вытесненной
воды превосходил объём железа в 8 раз.
-
На чашке весов
стоит стакан с водой. В стакан опускают
тело, удерживая его на нити так, что оно
не касается ни дна, ни стенок стакана.
Изменятся ли показания весов?
При условии, что
груз находится над поверхностью воды
в стакане, показания весов не изменятся,
т. к. груз не будет оказывать никакого
воздействия ни на стакан, ни на воду в
ней.
При условии, что
тело не вытесняет из стакана через край
в воду, вес оказываемый системой
“Стакан+вода+груз” будет равен весу
системы “Стакан+вода” и системы
“Вода, вытесняемая грузом”.
При условии, что
груз вытеснит воду в через край в объёме
равном объёму погружённой части груза,
равновесие весов не изменится.
Измерение массы и объема. Плотность вещества
- Закон инерции
- Инертность тела
- Инертная и гравитационная масса
- Измерение массы с помощью весов
- Плотность вещества
- Задачи
- Лабораторная работа №5. Определение плотности жидкостей
- Лабораторная работа №6. Определение плотности твердых тел
п.1. Закон инерции
Как свидетельствуют многочисленные эксперименты и наш повседневный опыт, чтобы неподвижное тело сдвинулось с места, на него должно подействовать другое тело. С другой стороны, чтобы остановить тело, уже находящееся в движении, или изменить его траекторию, также необходимо внешнее воздействие (обычно, причиной остановки в механике является трение; причиной изменения траектории – столкновение с другим телом и т.п.).
Возникает вопрос: а что будет с телом, если на него не действуют никакие другие тела?
Очевидно, если тело покоилось, то оно продолжит покоиться.
А если оно двигалось, что тогда произойдет?
А теперь представим себе идеальный случай: трение полностью отсутствует.
В этом случае шарик будет двигаться с постоянной скоростью бесконечно долго.
Закон инерции
Если на тело не действуют другие тела, оно либо покоится, либо движется прямолинейно и равномерно.
Закон инерции впервые был сформулирован Галилео Галилеем в его работе «Диалог о двух главнейших системах мира» (опубликована в 1632 г.). Однако Галилей ошибочно считал, что свободное равномерное движение тела возможно не только по прямой, но и по окружности.
В 1644 г. Рене Декарт уточнил формулировку Галилея, указав, что для изменения направления скорости также необходимо внешнее воздействие. Т.к. при равномерном движении по окружности направление скорости всё время меняется, оно не является свободным. Следовательно, свободное движение может быть только прямолинейным.
п.2. Инертность тела
Инертность – это свойство тела сохранять состояние покоя или прямолинейное и равномерное движение.
Благодаря инертности, тело не может мгновенно перейти из состояния покоя в движение или из состояния движения в покой. Для изменения скорости тела необходимо определенное время.
При взаимодействии инертность проявляется в том, что разные тела под одинаковым внешним воздействием получают разные ускорения (об ускорении – см. §11 данного справочника).
п.3. Инертная и гравитационная масса
Инертная масса – это количественная мера инертности, показатель того, в какой степени данное тело будет препятствовать изменению своей скорости.
Гравитационная масса – это количественная характеристика способности тела к взаимодействию по закону всемирного тяготения.
На сегодняшний день с высоким уровнем точности (относительная ошибка (sim 10^{-13}) в эксперименте 2009 г.) установлено, что значения инертной и гравитационной массы одного и того же тела равны. Поэтому инертную и гравитационную массы на практике не различают (принцип эквивалентности) и рассматривают «просто» массу тела.
Единицей массы в системе СИ является килограмм (кг).
Масса является одной из семи основных единиц системы СИ (см. §2 данного справочника).
При изучении очень больших или очень малых физических тел удобней использовать внесистемные единицы массы.
Например, в астрофизике единицей для сравнения масс небесных тел служит масса Солнца, (M_{odot}approx 1,99cdot 10^{30} text{кг}). А в физической химии при определении масс атомов и молекул используется атомная единица массы, равная 1/12 массы свободного покоящегося атома углерода, (1 text{а.е.м.}approx 1,66cdot 10^{-27} text{кг}).
п.4. Измерение массы с помощью весов
Весы – это прибор для измерения массы по весу тела на основании принципа эквивалентности инертной и гравитационной масс.
 Весы равноплечие рычажные лабораторные и наборы гирек к ним |
Вес тела определяется сравнением с весом эталонной массы (гири). Весы находятся в равновесии, если помещенные на их чаши тела одинаково притягиваются к Земле. Чтобы найти массу тела, его кладут на одну чашу весов, а на другую – гири известной массы, пока весы не уравновесятся. |
Метод двойного взвешивания (метод Гаусса)
Шаг 1. Поместить тело для взвешивания на левую чашку весов, а на правую чашку весов поставить гири до полного уравновешивания. Записать полученный результат (m_1).
Шаг 2. Переложить тело на правую чашку весов, а гири – на левую. Повторить уравновешивание. Записать полученный результат (m_2).
Шаг 3. Найти массу тела как среднее арифметическое $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ т.к. (delta_m=0,01text{%}) – относительная погрешность для весов класса точности III.
п.5. Плотность вещества
Плотность вещества однородного тела – это физическая величина, равная отношению массы тела к его объему: $$ rho=frac mv $$
Единицей плотности в системе СИ является килограмм на метр кубический (кг/м3).
Плотности различных веществ тщательно измерены и занесены в справочные таблицы.
Плотности в справочнике даны для химически чистых веществ (содержание основного вещества 98% и выше), при нормальных условиях (давление 760 мм рт.ст. и температура 0°С), если не указаны другие значения давления и температуры.
Плотность зависит от следующих свойств вещества:
- масса молекул (атомов) вещества. Например, масса атомов алюминия 27 а.е.м., а атомов золота 197 а.е.м. При этом плотность алюминия 2700 кг/м3, а плотность золота 19300 кг/м3, что приблизительно соответствует соотношению масс атомов. Небольшое различие можно объяснить большим расстоянием между более крупными атомами золота в кристаллической решетке (гранецентрированный куб, как для алюминия, так и для золота).
- расположение частиц вещества. Например, расстояния между слоями атомов углерода в графите в 3 раза больше, чем межатомные расстояния в самих слоях; а вот в алмазе атомы углерода упакованы очень плотно. В результате плотность графита 2160 кг/м3, а плотность алмаза 3510 кг/м3, хотя оба вещества состоят из атомов углерода.
- агрегатное состояние, в котором находится вещество. Наименьшие плотности у газов, наибольшие – у твердых веществ. Например, плотность воздуха (газ) 1,29 кг/м3, плотность воды (жидкость) 1000 кг/м3, плотность железа (твердое тело) 7900 кг/м3.
п.6. Задачи
Задача 1. Найдите плотность мела, если масса кусочка равна 7,2 г, а объем – 3,6 см3.
Дано:
(m=7,2 text{г}=7,2cdot 10^{-3} text{кг})
(V=3,6 text{см}^3=3,6cdot 10^{-6} text{м}^3)
__________________
(rho-?)
Плотность (rho=frac mv) $$ rho=frac{7,2cdot 10^{-3}}{3,6cdot 10^{-6}}=2cdot 10^3=2000 (text{кг/м}^3) $$ Ответ: (2000 text{кг/м}^3)
Задача 2. Найдите объем тела человека массой 60 кг, ели средняя плотность человеческого тела равна плотности воды. Ответ дайте в литрах.
Дано:
(m=60 text{кг})
(rho=1000 text{кг/м}^3)
__________________
(V-?)
Плотность (rho=frac mv Rightarrow) Объем (V=frac mp) $$ V=frac{60}{1000}=0,06 (text{м}^3)=60 (text{л}) $$ Ответ: 60 л.
Задача 3. Алюминиевая кастрюля имеет массу 0,5 кг. Если кастрюлю таких же размеров изготовить из стали, какая у неё будет масса?
Дано:
(m_1=0,5 text{кг})
(rho_1=2700 text{кг/м}^3)
(rho_2=7800 text{кг/м}^3)
__________________
(m_2-?)
У кастрюль одинаковых размеров одинаковый объем. Получаем: begin{gather*} V=frac{m_1}{rho_1}=frac{m_2}{rho_2}Rightarrow m_2=frac{rho_2}{rho_1}m_1\ m_2=frac{7800}{2700}cdot 0,5approx 1,4 (text{кг}) end{gather*} Ответ: ≈1,4 кг.
Задача 4*. В банку, до краев наполненную водой, опустили кусок золота массой 1 кг. В другую такую же банку опустили кусок меди массой 1 кг. Где больше вылилось воды и насколько больше? (ответ дайте в миллилитрах).
Дано:
(m=1 text{кг})
(rho_1=19320 text{кг/м}^3)
(rho_2=8940 text{кг/м}^3)
__________________
(Delta V-?)
Объем вытесненной воды равен объему погруженного тела: $$ V_1=frac{m}{rho_1}, V_2=frac{m}{rho_2} $$ Т.к. (rho_1gt rho_2, V_1lt V_2), объем воды, вытесненной медью, больше. $$ Delta V=V_2-V_1=frac{m}{rho_2}-frac{m}{rho_1}=mleft(frac{1}{rho_2}-frac{1}{rho_2}right)=mfrac{rho_1-rho_2}{rho_1rho_2} $$ Подставляем: begin{gather*} Delta V=1cdotfrac{19320-8940}{19320cdot 8940}approx 6,01cdot 10^{-5} text{м}^3\ 1 text{л}=10^{-3} text{м}^3, 1 text{мл}=1 text{cм}^3=10^{-3} text{л}=10^{-6} text{м}^3\ Delta Vapprox 60,1 text{мл} end{gather*} Ответ: ≈60,1 мл; больше вылилось во втором случае, для меди.
п.7. Лабораторная работа №5. Определение плотности жидкостей
Цель работы
Научиться измерять массу и объем жидкостей. Научиться определять жидкости по плотности, оценивать погрешность полученных результатов.
Теоретические сведения
Для определения массы тел в данной работе используется метод двойного взвешивания (см. выше в данном параграфе).
Масса тела определяется как среднее арифметическое двух взвешиваний на разных чашках весов: $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ Пусть масса стакана с жидкостью равна (M), абсолютная погрешность этого взвешивания (Delta M); масса пустого стакана (m_{text{ст}}), абсолютная погрешность (Delta m_{text{ст}}). Тогда масса жидкости $$ m=M-m_{text{ст}} $$ Абсолютная и относительная погрешности определения массы жидкости $$ Delta m=Delta M+Delta m_{text{ст}}, delta_m=frac{Delta m}{m}cdot 100text{%} $$ Мерный цилиндр проградуирован в миллилитрах. Для расчёта плотности жидкости в системе СИ необходимо помнить, что $$ 1 text{мл}=1 text{cм}^3=10^{-6} text{м}^3 $$ Абсолютная погрешность измерения объема жидкости равна половине цены деления мерного цилиндра $$ Delta V=frac d2 $$ Относительная погрешность равна $$ delta_V=frac{Delta V}{V}cdot 100text{%}. $$ Плотность жидкости равна $$ rho=frac mv. $$ Относительная погрешность результата $$ delta_{rho}=delta_m+delta_V. $$ Абсолютная погрешность результата $$ Deltarho=rhocdot delta_{rho} $$ Перевод полученных результатов в систему СИ $$ 1frac{text{г}}{text{см}^3}= frac{10^{-3} text{кг}}{10^{-6} text{м}^3}=10^3frac{text{кг}}{text{м}^3}=1000frac{text{кг}}{text{м}^3} $$
Приборы и материалы
Два стакана с неизвестными жидкостями; мерный цилиндр; весы с разновесом.
Ход работы
1. Приготовьте весы к взвешиванию.
2. Поставьте на весы первый стакан с жидкостью. Методом двойного взвешивания определите массу стакана и жидкости (M_1). Оцените абсолютную погрешность взвешивания.
3. Вылейте жидкость из первого стакан в мерный цилиндр и определите её объем (V_1). Оцените абсолютную погрешность измерения объема.
4. Методом двойного взвешивания определите массу первого стакана (m_{text{ст1}}). Оцените абсолютную погрешность взвешивания.
5. По формулам, данным в теоретической части, определите плотность жидкости, относительную и абсолютную погрешности полученного результата.
6. По таблице в справочнике определите, какая жидкость находится в первом стакане.
7.-11. Повторите шаги 2.-6. для второго стакана с жидкостью.
12. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Цена деления мерного цилиндра (d=1 text{мл}=1 text{см}^3)
Первый стакан
| Стадии двойного взвешивания | (M, text{г}) | (m_{text{ст}}, text{г}) |
| (m_1) | 151,2 | 50,1 |
| (m_2) | 150,8 | 49,9 |
| (m=frac{m_1+m_2}{2}) | 151,0 | 50,0 |
| (|m_1-m_2|) | 0,4 | 0,2 |
| (0,01text{%}m) | 0,015 | 0,005 |
| (Delta m) | 0,4 | 0,2 |
Масса первой жидкости
begin{gather*} m=151,0-50,0=101,0,\ Delta m=0,4+0,2=0,6,\ delta_m=frac{0,6}{101,0}cdot 100text{%}=0,59text{%} end{gather*}
Объем первой жидкости
begin{gather*} V=109 text{мл},\ Delta V=frac d2=0,5 text{мл},\ delta_V=frac{0,5}{109}cdot 100text{%}=0,46text{%} end{gather*}
Плотность первой жидкости
begin{gather*} rho=frac mV=frac{101,0}{109}approx 0,927frac{text{г}}{text{см}^3}=927frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,59text{%}+0,46text{%}approx 1,1text{%},\ delta rho=rhocdotdelta_{rho}=927cdot 0,011approx 10frac{text{кг}}{text{м}^3},\ rho=(927pm 10)frac{text{кг}}{text{м}^3},\ delta_{rho}=1,1text{%} end{gather*}
В первом стакане – подсолнечное масло.
Второй стакан
| Стадии двойного взвешивания | (M, text{г}) | (m_{text{ст}}, text{г}) |
| (m_1) | 100,4 | 50,0 |
| (m_2) | 100,2 | 49,9 |
| (m=frac{m_1+m_2}{2}) | 100,3 | 49,95≈50,0 |
| (|m_1-m_2|) | 0,2 | 0,1 |
| (0,01text{%}m) | 0,01 | 0,005 |
| (Delta m) | 0,2 | 0,1 |
Масса второй жидкости
begin{gather*} m=100,3-50,0=50,3,\ Delta m=0,2+0,1=0,3,\ delta_m=frac{0,3}{50,3}cdot 100text{%}=0,6text{%} end{gather*}
Объем второй жидкости
begin{gather*} V=50 text{мл},\ Delta V=frac d2=0,5 text{мл},\ delta_V=frac{0,5}{50}cdot 100text{%}=1,0text{%} end{gather*}
Плотность второй жидкости
begin{gather*} rho=frac mV=frac{50,3}{50,0}= 1,006frac{text{г}}{text{см}^3}=1006frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,6text{%}+1,0text{%}= 1,6text{%},\ delta rho=rhocdotdelta_{rho}=1006cdot 0,016approx 16frac{text{кг}}{text{м}^3},\ rho=(1006pm 16)frac{text{кг}}{text{м}^3},\ delta_{rho}=1,6text{%} end{gather*}
Во втором стакане – вода.
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для определения плотности жидкости в работе методом двойного взвешивания измерялась масса (стакана с жидкостью и пустого стакана) и объем жидкости в мерном цилиндре.
Результаты для двух данных жидкостей
begin{gather*} rho_1=(927pm 10)frac{text{кг}}{text{м}^3}, delta_{rho 1}=1,1text{%}\ rho_2=(1006pm 16)frac{text{кг}}{text{м}^3}, delta_{rho 2}=1,6text{%} end{gather*}
По таблицам в справочнике было определено, что в первом стакане – растительное масло, а во втором – вода. Полученные результаты также подтверждаются цветом (желтоватый – для масла, прозрачный – для воды) и запахом (характерный запах у масла и отсутствие запаха у воды).
п.8. Лабораторная работа №6. Определение плотности твердых тел
Цель работы
Научиться измерять массу и объем твердых тел неправильной формы. Научиться определять вещества твердых тел по плотности, оценивать погрешность полученных результатов.
Теоретические сведения
Для определения массы тел в данной работе используется метод двойного взвешивания (см. выше в данном параграфе).
Масса тела определяется как среднее арифметическое двух взвешиваний на разных чашках весов: $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ Относительная погрешность $$ delta_m=frac{Delta m}{m}cdot 100text{%} $$ Объем твердого тела неправильной формы определяется с помощью погружения в жидкость.
Пусть объем жидкости в мерном цилиндре до погружения тела (V_0), после погружения – (V’).
Тогда объем самого тела (V=V’-V_0).
Абсолютная погрешность измерения объема равна половине цены деления мерного цилиндра (Delta V_0=frac d2) для прямого измерения. Для разности двух прямых измерений общая абсолютная погрешность $$ Delta V=2Delta V_0=d $$ Относительная погрешность $$ delta_V=frac dVcdot 100text{%}. $$ Плотность твердого тела равна $$ rho=frac mv. $$ Относительная погрешность результата $$ delta_{rho}=delta_m+delta_V. $$ Абсолютная погрешность результата $$ Deltarho=rhocdot delta_{rho} $$ Перевод полученных результатов в систему СИ $$ 1frac{text{г}}{text{см}^3}= frac{10^{-3} text{кг}}{10^{-6} text{м}^3}=10^3frac{text{кг}}{text{м}^3}=1000frac{text{кг}}{text{м}^3} $$
Приборы и материалы
Мерный цилиндр, наполненный водой наполовину; два тела неправильной формы из металлов; весы с разновесом.
Ход работы
1. Приготовьте весы к взвешиванию.
2. Методом двойного взвешивания определите массу первого тела. Найдите абсолютную и относительную погрешность взвешивания.
3. С помощью погружения первого тела в жидкость найдите его объем. Абсолютная погрешность равна цене деления мерного цилиндра. Рассчитайте относительную погрешность.
4. По формулам, данным в теоретической части, определите плотность твердого тела, относительную и абсолютную погрешности полученного результата.
5. По таблице в справочнике определите, из какого вещества изготовлено первое тело.
6-9. Повторите шаги 2.-5. для второго твердого тела неправильной формы.
10. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Цена деления мерного цилиндра (d=0,5 text{мл}=0,5 text{см}^3)
Первое тело
| Стадии двойного взвешивания | (m, text{г}) |
| (m_1) | 22,34 |
| (m_2) | 22,38 |
| (m=frac{m_1+m_2}{2}) | 22,36 |
| (|m_1-m_2|) | 0,04 |
| (0,01text{%}m) | 0,002 |
| (Delta m) | 0,04 |
| (delta m) | 0,18% |
| Стадии определения объема | (V, text{см}^3) |
| (V_0) | 50,0 |
| (V’) | 58,5 |
| (V=V’-V_0) | 8,5 |
| (Delta V=d) | 0,5 |
| (delta_V) | 5,9% |
Плотность первого тела
begin{gather*} rho=frac mV=frac{22,36}{8,5}approx 2,631frac{text{г}}{text{см}^3}=2631frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,18text{%}+5,9text{%}approx 6,1text{%},\ delta rho=rhocdotdelta_{rho}=2631cdot 0,061approx 160frac{text{кг}}{text{м}^3},\ rho=(2630pm 160)frac{text{кг}}{text{м}^3},\ delta_{rho}=6,1text{%} end{gather*}
Первое тело изготовлено из алюминия.
Второе тело
| Стадии двойного взвешивания | (m, text{г}) |
| (m_1) | 101,21 |
| (m_2) | 101,27 |
| (m=frac{m_1+m_2}{2}) | 101,25 |
| (|m_1-m_2|) | 0,06 |
| (0,01text{%}m) | 0,005 |
| (Delta m) | 0,06 |
| (delta m) | 0,06% |
| Стадии определения объема | (V, text{см}^3) |
| (V_0) | 50,0 |
| (V’) | 63,0 |
| (V=V’-V_0) | 13,0 |
| (Delta V=d) | 0,5 |
| (delta_V) | 3,8% |
Плотность второго тела
begin{gather*} rho=frac mV=frac{101,25}{13,0}approx 7,788frac{text{г}}{text{см}^3}=7788frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,06text{%}+3,8text{%}approx 3,9text{%},\ delta rho=rhocdotdelta_{rho}=7788cdot 0,039approx 300frac{text{кг}}{text{м}^3},\ rho=(7790pm 300)frac{text{кг}}{text{м}^3},\ delta_{rho}=3,9text{%} end{gather*}
Второе тело изготовлено из железа.
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для определения плотности твердых металлических тел неправильной формы в работе методом двойного взвешивания измерялась масса тел. Объем определялся методом погружения в мерном цилиндре.
Результаты для двух данных тел
begin{gather*} rho_1=(2630pm 160)frac{text{кг}}{text{м}^3}, delta_{rho 1}=6,1text{%}\ rho_2=(7790pm 300)frac{text{кг}}{text{м}^3}, delta_{rho 2}=3,9text{%} end{gather*}
По таблицам в справочнике было определено, что первое тело изготовлено из алюминия, второе – из железа.
Онлайн-калькулятор плотности, который поможет вам определить соотношение между плотностью, массой и весом объекта с помощью формулы плотности. В этом калькуляторе есть небольшая, но очень важная опция, где вы можете легко определить плотность объекта по категории и названию материала. Если вы хотите получить краткие сведения о том, как рассчитать плотность по формуле, продолжайте читать!
Кроме того, вы можете попробовать наш онлайн-калькулятор импульса, который поможет вам найти импульс движущегося объекта, а также определить массу объекта.
Читать дальше!
Что такое формула плотности?
Расчеты не слишком сложные, а очень простые. Просто введите значения в следующее уравнение плотности, чтобы легко вычислить любую из требуемых переменных:
р = м / В
Где,
V – объем & m – масса объекта.
Если вы хотите найти объем с помощью плотности и массы, калькулятор плотности использует формулу:
V = м / п
Чтобы найти массу с плотностью и объемом, рассмотрите следующую формулу:
т = р * V
Плотность можно определить как массу на единицу объема объекта. Со значениями введите единицы измерения, и этот калькулятор выполнит преобразование единиц измерения.
Как найти плотность объекта по массе и объему (шаг за шагом):
Рассчитать плотность с помощью этого расчет плотности очень просто. Вы можете найти любое из трех значений, введя два значения в формулу. Вот пример для каждого расчета:
Проведите по!
Пример:
Объект весил около 150 г и объем 90 см3. Найти плотность объекта?
Решение:
Формула:
р = м / В
Вот,
m = 150 г
V = 90 см3
Так,
р = 150/90
p = 1,66 г · см-3
как определить плотность объем по и массе:
Вы можете легко определить объем объекта, изменив уравнение плотности. Давайте посмотрим на пример:
Пример:
Какой у тела объем, если его масса 500 г, а плотность 4 см-3?
Решение:
Формула:
V = м / п
Вот,
м = 500г
р = 4 см-3
Так,
V = 500/4
V = 125 см3
Как найти массу объекта с учетом плотности и объема:
Расчет массы по объему и плотности становится простым. Просто следуйте следующему примеру:
Пример:
Объем объекта 200 см3, а плотность 9 см-3, какова масса объекта?
Решение:
Формула:
т = р * V
Вот,
V = 200 см3
р = 9 см-3
Так,
т = (9) * (200)
м = 1800г
Какая плотность воды?
Плотность воды между 0 ° C и 4 ° C обычно составляет 100 кг / м3, но она меняется в зависимости от температуры. При повышении температуры объем материала увеличивается. Согласно формуле, объем и плотность обратно пропорциональны друг другу, в конечном итоге плотность материала уменьшается. Плотность воды при различных температурах приведена в следующей таблице:
Стол
Ниже приведена таблица единиц, в которой плотность обычно выражается плотностями некоторых материалов.
Столы
Как пользоваться калькулятором плотности:
Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!
Входы:
- Прежде всего, выберите во вкладке то, что вам нужно найти.
- Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
- Наконец, нажмите кнопку “Рассчитать”.
Выходы:
Как только вы заполните все поля, калькулятор покажет:
- Плотность объекта
- Масса объекта
- Объем объекта
- Корень кубический из объема
Заметка:
Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.
Заключение:
Плотности широко используются для идентификации чистых веществ и определения состава различных видов смесей. В реальной жизни это полезно, когда выясняется, что что-то будет плавать в воде, и важно при расчете объема и массы вещества. Когда дело доходит до расчетов, запишите онлайн-калькулятор плотности, который поможет вам в кратчайшие сроки найти взаимосвязь между массой, объемом и плотностью вещества.
Others Languages:Density Calculator, Yoğunluk Hesaplama, Kalkulator Gęstości, Kalkulator Kepadatan, Dichte Rechner, 密度 計算, 밀도 계산, Výpočet Hustoty, Cálculo De Densidade, Calcul Densité, Calculadora De Densidad, Calcolo Densità, حساب الكثافة, Tiheys Laskuri, Massefylde Beregning, Tetthets Kalkulator.
С древних времен люди замечали, что всякий брошенный вверх предмет неминуемо падает вниз, на землю. Это явление в современной физике описывается в рамках классической механики с привлечением понятия гравитационного притяжения нашей планетой всех окружающих тел. С силой гравитации тесно связан вес тела. В данной статье рассмотрим эту физическую величину и приведем формулы веса.
Что такое вес тела?
Прежде чем приводить формулу веса в физике, рассмотрим определение самой величины. Весом называют силу, с которой тело воздействует на опору либо растягивает подвес, к которому оно прикреплено. В этом принципиальное отличие веса тела от массы. Последняя является физической характеристикой инерционных свойств объектов. Масса – это неотъемлемое свойство тел, вес же – это величина переменная, поскольку она зависит от характеристик гравитационного поля, в котором находится рассматриваемое тело.
Примером действия веса является ситуация, когда мы становимся на весы. Хотя последние откалиброваны таким образом, что они показывают массу в килограммах, в действительности же измеряется именно вес, с которым наше тело давит на весы.

Другой пример – это взвешивание предметов с помощью ручных пружинных весов, которые называют кантером. Подвешенный к прибору предмет растягивает пружину до тех пор, пока сила ее упругости не уравновесит вес тела. Эти весы, как и предыдущие, откалиброваны на шкалу массы.
Формула веса тела в покое
В середине XVII века, наблюдая за поведением небесных тел (планет, естественных спутников, комет) и используя экспериментальные данные, Исаак Ньютон сформулировал закон всемирного тяготения. Благодаря этому закону появилась возможность численного расчета гравитационных сил, с которыми взаимодействуют тела в природе. Согласно этому закону, сила тяжести Ft на поверхности любой планеты может быть рассчитана по формуле:
Ft = m*g
Где m – масса тела, g – это линейное ускорение, которое планета сообщает всем телам, находящимся вблизи нее. Для Земли оно равно 9,81 м/с2. Сразу отметим, что величина g от массы не зависит, однако она зависит от расстояния до планеты, убывая, как его квадрат.
Когда любое тело массой m находится на поверхности, например стакан с водой стоит на столе, то на него действуют две силы:
- тяжести Ft;
- реакции опоры N.
Так как тело никуда не движется и покоится, то обе силы противоположны по направлению и равны по модулю, то есть:
- Ft = N
Согласно определению веса, формула для него принимает вид:
P = N = Ft = m*g
Именно с силой Ft стакан с водой давит на стол.
Свободное падение и вес тела
Проведем следующий мысленный эксперимент: предположим, что в деревянный ящик поместили камень некоторой массы m, затем бросили этот ящик с высоты. Какой вес будет иметь камень в процессе свободного падения?
Для ответа на этот вопрос следует записать основное уравнение динамики. В данном случае оно имеет вид:
m*a = Ft – N
Здесь a – ускорение, с которым падает ящик и камень. В случае свободного падения, это ускорение равно величине g. Тогда получаем:
m*g = m*g – N =>
N = 0
То есть сила реакции опоры равна нулю. Этот вывод уравнения движения говорит о том, что камень во время свободного падения давить на дно ящика не будет, то есть его вес будет равным нулю. Такая ситуация наблюдается на космических станциях, на которых центробежная сила и сила тяжести уравновешивают друг друга.

Для движения с произвольным ускорением вниз формула веса примет вид:
P = m*(a – g)
Решение задачи
Известно, что во время старта ракеты ее ускорение равно 40 м/с2. Необходимо определить вес космонавта, находящегося в ней, если его масса равна 70 кг.
Для начала запишем второй закон Ньютона для рассматриваемой задачи. Имеем:
m*a = N – m*g
Здесь сила тяжести направлена против ускорения, а реакция опоры – вдоль вектора ускорения. Из этого равенства получаем:
P = N = m*(g + a)

Подставляя данные, получаем, что вес космонавта во время старта ракеты будет равен 3486,7 Н. Если бы в процессе старта космонавт встал на весы, то они бы показали значение его массы 355,4 кг.
Как найти плотность тела
При решении некоторых физических задач требуется найти плотность тела. Иногда плотность физического тела необходимо определить и на практике, например, для того чтобы узнать, утонет оно или нет. Кстати, тело человека также можно отнести к физическим телам. Причем понятие «плотности» человеческого тела давно уже вошло в обиход. Так «крепко сбитого» человека обычно называют «плотным», а того, кто имеет противоположную конституцию тела – «рыхлым».
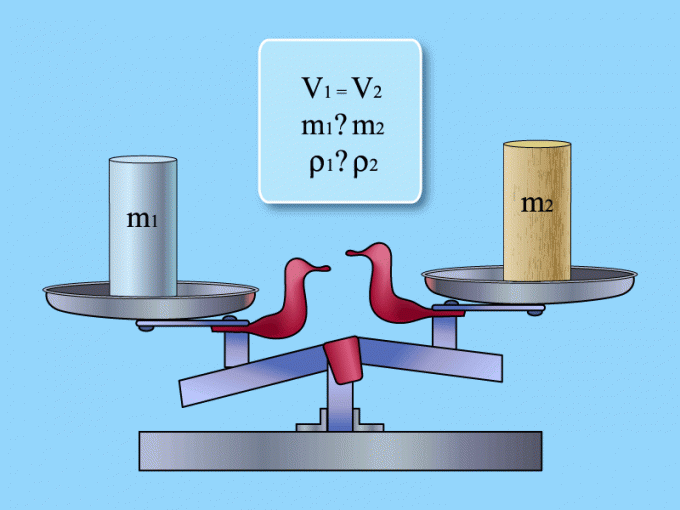
Вам понадобится
- калькулятор, весы, линейка, мерная кружка, таблица плотности веществ.
Инструкция
Чтобы найти плотность физического тела, определите из какого вещества или материала оно состоит. Затем возьмите таблицу плотности веществ и найдите в ней соответствующее вещество. Так, например, если предмет изготовлен из алюминия, его плотность будет равна 2,7 г/см³.
Если тело состоит из нескольких веществ, то найдите в соответствующих таблицах плотность каждого из них. Чтобы найти плотность тела в целом, определите вклад каждого вещества в формирование плотности предмета. Для этого определите объем или массу каждой однородной части, а затем посчитайте массу и объем всего тела.
Пусть, например, тело состоит из двух частей массой m1 и m2, соответственно. Плотность каждой части – ρ1 и ρ2. Чтобы найти среднюю плотность тела, найдите общий объем: V = V1 + V2 = m1 * ρ1 + m2 * ρ2, а затем разделите на общую массу тела (m = m1 + m2): ρ = V / m = (m1 * ρ1 + m2 * ρ2) / (m1 + m2), где:V – общий объем тела;
V1 и V2 – объем первой и второй части тела соответственно;
m – общая масса тела;
m1 и m2 – масса первой и второй части тела соответственно;
ρ – средняя плотность тела;
ρ1 и ρ2 – плотность первой и второй части тела соответственно.
Если известны объемы (V1 и V2) каждой части тела, а также их плотности, для вычисления плотности тела воспользуйтесь аналогичной формулой:ρ = V / m = (V1 + V2) / (m1 + m2) = (V1 + V2) / (V1 / ρ1 + V2 / ρ2). Обозначения параметров те же, что и в предыдущей формуле.
Если материал (вещество), из которого состоит тело, неизвестен или имеет непостоянную плотность (например, дерево, плотность которого зависит от влажности), чтобы найти его плотность, определите его объем и разделите на массу. То есть воспользуйтесь формулой:ρ = V / m.Для этого, конечно, придется посчитать или измерить объем и массу тела, зато такой метод даст самый точный результат. Если тело имеет форму простой геометрической фигуры, посчитайте его объем, воспользовавшись соответствующими формулами стереометрии. Объем сложных тел определите через объем вытесненной ими жидкости. Массу тела найдите с помощью взвешивания.
Источники:
- как определить плотность тела
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
 ж‘,
ж‘,