Как найти плотность потока мощности

Как найти плотность потока мощности

Чтобы наземные
устройства могли принимать сигналы со
спутника, необходимо создать у поверхности
Земли определенную напряженность
электромагнитного поля (или плотность
потока мощности электромагнитных волн).
Мощность электромагнитных волн,
излучаемых антенной, является важнейшей
характеристикой передающей системы.
Излучать их равномерно во все стороны,
то есть изотропно,
при спутниковом
телевизионном вещании нецелесообразно
и в большинстве случаев недопустимо.
Поэтому излучаемая энергия электромагнитных
волн концентрируется антенной в узкий
луч и направляется на выбранную земную
поверхность.

В этом случае для
ее оценки пользуются понятием эквивалентной
изотропной излучаемой мощности ЭИИМ.
ЭИИМ (Е)
показывает, какую мощность пришлось бы
иметь передатчику искусственного
спутника, если бы излучение велось
изотропно, все направленно. Однако
благодаря направленным свойствам
антенны, требуемая мощность излучения
меньше на коэффициент ее усиления.
Уровень энергии электромагнитных волн
в точке приема на поверхности Земли
зависит от рассеяния
энергии по
мере удаления от спутника и дополнительных
ее потерь в атмосфере Земли. Уровень
энергии, падающей на перпендикулярную
к потоку поверхность, отнесенный к
площади этой поверхности, называется
плотностью потока мощности — ППМ (W).
Для определения ППМ в месте приема, если
известны значения ЭИИМ, пользуются
формулой:

W (дБ Вт/м ) = Е (дБ
Вт) — 10 Ig (
) — Lдоп
(дБ Вт/м ) (2.2)

Первое вычитаемое
определяет потери на рассеяние. Второе—
учитывает потери в атмосфере Земли,
поэтому приведенная фор- мула справедлива
для любой погоды. При расчетах для ясной
погоды второе вычитаемое отсутствует.
Расстояние до спутника принимается
равным CI = 3,7 10′ м.

Более точно
расстояние можно определить по формуле:

d=rs

(2.3)

где rs
= 42164 км —
расстояние от центра Земли до
геостационарной орбиты (экваториальный
радиус);
=
(L-S) — разность
между географической долготой точки
приема (L) и долготой спутника (S);
θ,— географическая широта точки приема;
0,1513 — частное от деления радиуса Земли
на траекторию движения спутника.

Для определения
значения плотности потока мощности по
известной величине эквивалентно
изотропной излучаемой мощности (без
учета потерь) можно руководствоваться
упрощенной формулой (2.4) или графической
зависимостью, представленной на рис.
2.3

W (дБ Вт /м ) = Е (дБ
Вт) — 153,0.

Плотность потока
мощности является очень важной
характеристикой для приема со
спутников-ретрансляторов. Она позволяет
оценить возможность уверенного приема
в данной географической точке на антенну
соответствующего размера и при выбранных
значениях коэффициента шума и усиления
малошумящего усилителя- конвертера.
Величина плотности потока мощности
влияет на систему спутникового
телевизионного вещания. Увеличение ее
приводит к упрощению и удешевлению
наземных приемных устройств, однако
усложняет и повышает стоимость передающих
систем спутника. Уменьшение ППМ, наоборот,
удорожает наземные приемные устройства
при одновременном удешевлении спутника.
Необходимая ППМ у поверхности Земли
определена путем экономических расчетов
с оптимизацией стоимости как приемных
наземных устройств, так и передающих
спутниковых систем и выбрана с учетом
электромагнитной совместимости с
наземными службами, т.е. с учетом
минимальных взаимных помех.

Для индивидуальных
приемных устройств значение ППМ согласно
плана ВАКР-77 (Всемирной Административной
Конференции по радио) на границе зоны
покрытия должно быть минус 103 дБ Вт/м, а
для систем коллективного приема минус
111 дБ Вт/м .

Форма зоны покрытия
зависит от точки пересечения (точки
прицеливания) основного
лепестка излучения антенны спутника с
земной поверхностью. Например, точка
прицеливания российского спутника
ГАЛС-1 находится между Москвой и Саратовом
и форма зоны покрытия представляет
собой вытянутый эллипс.

Границы зоны
покрытия очерчены контурами на
географической карте с определенными
уровнями ППМ или ЭИИМ. Размеры ее
стремятся сделать минимальными, чтобы
снизить необходимую мощность передатчика
спутника с целью его удешевления.

На практике для
рассмотрения возможности приема в
данном месте с выбранного спутника
пользуются его трансляционными кривыми,
нарисованными на контурной географической
карте. Они представляют собой ряд
замкнутых линий с одинаковыми значениями
ППМ (ЭИИМ). В большинстве случаев на
картах вместо плотности потока мощности
отображаются значения ЭИИМ— проекция
(Footprint EIRP)
уровней ЭИИМ
в диапазоне от 40 до 53 дБ Вт.

Следует отметить,
что согласно предложениям ВАКР-77
нормируются значения ППМ, а не ЭИИМ
(табл.2.1). Нормирование вели- чины ППМ в
зоне приема связывается с углом возвышения
антенны (углом места) — y в направлении
на спутник. Допускаемая ППМ будет тем
больше, чем больше угол у, чем отвеснее
падают электромагнитные волны, т.е. чем
ближе точка приема расположена к
Экватору.

Согласно требованиям
ВАКР-77 предельная плотность потока
мощности частотно-модулированного
телевизионного сигнала для всех видов
телефонной связи в контрольной полосе
не должна превышать — 152 дБ. Вт/м’ -4,0 кГц.

Некоторые предельные
мешающие значения ППМ от спутников-
ретрансляторов для радиорелейных,
сотовых, спутниковых телефонных систем
и т.д. в зависимости от угла 0 (угла между
направлением прихода мешающей
электромагнитной волны и горизонтальной
плоскостью) приведены в табл.2.1.

Предельная
плотность потока мощности (W)

для угла θ, дБ-Вт/м

Как видно, плотности
потока мощности ограничиваются в
диапазонах частот выделенных для
спутников ФСС.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Макеты страниц

Рассмотрим теперь передачу звуковойэнергии по среде. Передача осуществляется звуковым давлением, совершающим работу при перемещении частиц среды, на которые оно действует. При расчете передаваемой энергии достаточно учитывать работу только звукового давления, потому что, как показано в предыдущем параграфе, работа равновесного давления приводит лишь к перераспределению энергии в среде.

Найдем мощность сил звукового давления, действующего на частицы, расположенные на какой-либо плоской элементарной площадке Сила звукового давления, действующая на площадку, равна Пусть скорость частиц, лежащих на этой площадке, равна тогда искомая мощность есть Эта мощность зависит от ориентировки площадки по тому же закону, что и поток массы среды, протекающей через эту площадку: Поэтому, по аналогии с применяемым в гидродинамике понятием вектора плотности потока импульса среды введем вектор плотности потока мощности:

Мощность сил давления, приложенных к площадке равна

(аналогично формуле, выражающей поток вещества через площадку:

Формулы (39.1), (39.2) — общие гидродинамические формулы, если есть полное давление; но мы будем относить величины только к акустическим величинам (так же, как плотность энергии в предыдущем параграфе): плотность потока звуковой мощности будем рассматривать как условную величину в том же смысле, как плотность звуковой энергии в среде.

В бегущей плоской волне модуль вектора равен

а сам вектор направлен по вектору медленности волны. Плотность потока мощности в направлении какой-либо оси координат, например оси равна

Плотности потока мощности плоских волн, бегущих в одном направлении, не аддитивны. Так, плотность потока мощности

волны равна

Аддитивность получится, если рассматривать средние за длительный промежуток времени потоки мощности для гармонических волн разных частот или для статистических волн при условии их статистической независимости. Здесь положение такое же, как и при расчете плотности энергии суммы двух волн.

Плотность потока мощности суперпозиции двух плоских волн, бегущих навстречу друг другу, всегда равна разности плотностей потоков мощности этих волн. В самом деле, в суммарном поле волн имеем

откуда

Между плотностью звуковой энергии в среде и плотностью потока звуковой мощности существует важное соотношение, аналогичное закону сохранения энергии в механике. Умножим уравнение движения

скалярно на вектор и уравнение неразрывности

на давление Складывая полученные уравнения, найдем

В скобках стоят соответственно плотность звуковой энергии Е и вектор плотности потока мощности Значит,

Это — дифференциальный закон сохранения звуковой энергии в среде.

Проинтегрируем это уравнение по какому-либо объему , ограниченному неподвижной поверхностью При интегрировании второго слагаемого можно преобразовать объемный интеграл в поверхностный.

Получим

Эта формула выражает интегральный закон сохранения энергии для звуковой энергии.

Этот «акустический» закон сохранения энергии пришлось выводить специально, вместо того чтобы сослаться прямо на «обычный» закон сохранения энергии, потому что как плотность энергии, так и плотность потока мощности берутся не полностью: учитывается только их квадратичная — «акустическая» — часть по отношению к давлению и скорости, а перераспределение энергии не учитывается.

Полученная формула относится к замкнутым объемам. Однако для бегущей плоской волны, ограниченной во времени, формулу можно применять и к незамкнутой поверхности. В самом деле, пусть имеется плоская звуковая волна, исчезающаяна некотором расстоянии слева и справа от данной точки. Проведем через эту точку плоскость, перпендикулярную к направлению распространения волны. Слева и справа от этой плоскости построим цилиндры, опирающиеся на эту плоскость, с осью, параллельной направлению распространения волны, и замкнем эти цилиндры достаточно далеко справа и слева от плоскости, где возмущение уже отсутствует или еще отсутствует. Рассматривая каждый из этих цилиндров как замкнутый объем и применяя к каждому из них закон сохранения акустической энергии, получим, что поверхностные интегралы сводятся к интегралам по общему основанию цилиндров, так как потоки через боковые и через далекие стенки равны нулю.

Теорему о сохранении акустической энергии можно поэтому трактовать как протекание энергии сквозь плоскость, перпендикулярную к направлению распространения волны: уменьшение энергии с одной стороны плоскости равно увеличению энергии с другой стороны.

Легко найти величину этого потокам так как для выбранной поверхности нормаль совпадает с направлением скорости частиц, то, согласно (38.2), в расчете на единицу площади поток через плоскость равен

В этой формуле существенно использование соотношения справедливого только в отсутствие дисперсии. Тогда плотность потока мощности оказывается равной плотности энергии, умноженной на скорость волны. Этот результат наглядно интерпретируется так: энергия в бегущей плоской волне переносится со скоростью звука.

Заметим, что в гармонической волне связать наличие потока мощности или усредненного потока мощности с каким-либо переносом энергии нельзя: так как в гармонической волне возмущение охватывает всю среду, то замкнуть цилиндры, о которых шла речь выше, так, чтобы их основания оказались вне области возмущения, невозможно. Если же замкнуть цилиндры внутри возмущенной области, то теорема сохранения выразит только, что в замкнутом объеме энергия бегущей гармонической волны не изменяется в среднем за период. Тем не менее в этом случае плотность энергии можно локализовать и для гармонической волны в каждый момент времени.

Если в среде имеется дисперсия, то уравнение (39.6) справедливо только для монохроматических волн, т. е. в случае, когда нельзя говорить о переносе энергии по среде. При этом следует еще иметь в виду, что величина с в (39.6) — разная для различных частот. Но формулу, аналогичную (39.6) и дающую скорость перемещения энергии по среде, можно получить для узкополосного сигнала — группы волн. В самом деле, в этом случае вся энергия сосредоточена в области, занятой группой, и эта группа перемещается с групповой скоростью и. Поэтому энергия волны также перемещается с групповой скоростью, и вместо формулы (39.6) имеем теперь

Для гармонических волн мощность какого-либо процесса удобно характеризовать ее средним значением за период или за промежуток времени, большой по сравнению с периодом. Задача о нахождении среднего по времени произведения двух гармонических величин одного периода часто возникает в теории колебаний: к ней сводятся все задачи о нахождении мощности гармонических процессов любой природы. В акустике одна из величин — давление, другая — скорость; при воздействии какой-либо гармонической силы на тело одна из величин — сама сила, другая — скорость тела; в электрических цепях одна их величин — разность потенциалов, а другая — сила тока. Дадим общее правило нахождения средней мощности во всех этих задачах, причем будем обозначать перемножаемые величины по-прежнему буквами и V, какова бы ни была их физическая природа.

Рассмотрим самый общий случай:

когда между исходными величинами имеется некоторый сдвиг фаз Амплитуды будем считать вещественными. Поскольку нахождение мощности есть нелинейная операция над гармоническими величинами и V, перейдем к вещественной

записи:

Мгновенная мощность процесса равна

При усреднении по периоду волны второе слагаемое в скобках даст нуль. Таким образом, средняя мощность процесса равна

В частном случае синфазности величин средняя мощность равна

В случае, когда сдвинуты по фазе на 90°, средняя мощность равна нулю.

Часто удобно вычислять мощность без перехода к вещественной записи: как легко получить из (39.8), Значит,

В ряде случаев одну из величин, например и, удобно представить в виде суммы двух слагаемых, из которых одно синфазно со второй величиной а другое сдвинуто относительно нее на 90°. В комплексной записи это значит, что одно слагаемое пропорционально а второе пропорционально . В этом случае говорят об «одинаковой мнимости» и о «разной мнимости» величин. Пусть, например, величины одинаковой, а и – разной мнимости. Мгновенная мощность равна

В первом слагаемом сдвиг фаз между сомножителями равен нулю, значит, средняя величина этого слагаемого равна

Среднее значение второго слагаемого равно нулю. Следовательно, средняя мощность всего процесса есть

Слагаемые в (39.13) соответствуют слагаемым в скобках в (39.9). Первое слагаемое в обеих формулах дает постоянную мощность, производящую накапливающуюся с течением времени работу; это так называемая активная мощность процесса. Второй член, дающий в среднем по времени нуль, называют реактивной мощностью. Соответственно компоненты называют активной и реактивной компонентами величины относительно величины принятой за основную. Можно было бы принять за основную величину и тогда представить в виде суммы активной и реактивной составляющих относительно Модуль активной компоненты каждой величины относительно второй из них равен амплитуде, умноженной на косинус угла сдвига фаз между величинами. Этот косинус равен отношению активной мощности к амплитуде реактивной мощности.

При комплексной записи часто удобно вводить импеданс — отношение величин

Импеданс гармонического процесса — в общем случае комплексная величина, не зависящая от времени. Средняя мощность процесса простым образом выражается через вещественную часть импеданса и амплитуду скорости. В самом деле, в общем случае (39.8)

и вещественная часть импеданса равна откуда, пользуясь (39.10), непосредственно получаем

Согласно (22.5) вектор скорости частиц в гармонической звуковой волне можно представить в виде суммы

Первое слагаемое имеет мнимость, отличную от давления, а второе — ту же мнимость, что и давление. Отсюда видно, что пространственное изменение амплитуды колебаний в волне не дает вклада в средний поток мощности, и он определяется только градиентом фазы и направлен вдоль этого градиента. Средний вектор плотности потока мощности равен

Например, в бегущей плоской гармонической волне и, следовательно,

(что, конечно, можно было получить и непосредственно из соотношения

В стоячей волне средняя плотность потока мощности равна нулю.

В неоднородной гармонической волне вектор потока средней мощности направлен вдоль вещественной 4 компоненты волнового вектора и, согласно (39.16), равен В перпендикулярном направлении, вдоль мнимой компоненты волнового вектора а, средний поток мощности равен нулю, так как скорость частиц в направлении а имеет другую мнимость, чем давление.

Воспользуемся полученными результатами, чтобы найти мощность, уносимую от плоскости спектрами — плоскими волнами, излучаемыми плоскостью, на которой заданы бегущие синусоидальные распределения давления или скорости. Пусть задано давление при. причем пусть Тогда нормальная компонента скорости частиц на плоскости равна , где угол скольжения данного спектра; скорость и давление синфазны и средняя плотность потока в направлении оси равна

Рис. 39.1. а — мощность излучения волной давления, бегущей плоскости, б – мощность излучения волной нормальных скоростей, бегущей по плоскости. Эффективность излучения выше при излучении волной нормальных скоростей и быстро растет при уменьшении угла скольжения излученной волны.

При изменении угла скольжения от 90° до нуля при неизменной амплитуде давления излучаемая в направлении оси z мощность падает от своего максимального значения до нуля, изменяясь по закону (рис. 39.1, а). Таким образом, при заданной амплитуде давления на плоскости наиболее эффективно излучение, перпендикулярное к плоскости, — поршневое излучение.

При нормальная скорость оказывается разной мнимости с давлением. Поэтому средняя излучаемая энергия в этом случае равна нулю: бесконечная плоскость, вдоль которой бежит синусоидальная волна давлений, ничего не излучает, если скорость бега волны меньше скорости звука в среде (длина волны возмущения на плоскости меньше длины волны звука той же частоты в среде).

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • ГЛАВА I. УПРУГИЕ ВОЛНЫ
  • § 1. Распространение упругих волн
  • § 2. Волновое поле. Частица среды
  • § 3. Задачи акустики
  • § 4. Скорость звуковых волн
  • § 5. Одномерная волна. Способ «остановки движения»
  • § 6. Поперечные волны на струне
  • § 7. Изгибные волны на стержне
  • § 8. Продольные плоские волны в жидкости
  • § 9. Волны малой амплитуды. Линеаризация
  • § 10. Замечание относительно закона Гука
  • ГЛАВА II. ОБЩИЕ УРАВНЕНИЯ АКУСТИКИ. ПЛОСКИЕ ВОЛНЫ
  • § 12. Граничные условия
  • § 13. Полная система акустических уравнений и ее упрощение (линеаризация). Особенность картины сплошной среды в акустике
  • § 14. Лапласова и ньютонова скорости звука. Температурные колебания в звуковой волне
  • § 15. Принцип суперпозиции волн
  • § 16. Волновое уравнение
  • § 17. Одномерная задача. Плоская волна
  • § 18. Гармонические плоские волны. Стоячие волны
  • § 19. Акустика микронеоднородных сред. Температурные и вязкие волны
  • § 20. Поршневое излучение плоской волны. Импульс бегущей плоской волны
  • ГЛАВА III. ГАРМОНИЧЕСКИЕ ВОЛНЫ
  • § 21. Гармонические волны
  • § 22. Комплексная запись гармонических волн
  • § 23. Разложение Фурье волны с произвольной зависимостью от времени
  • § 24. Спектральные разложения волн
  • § 25. Плоские гармонические волны
  • § 26. Сохранение формы бегущих гармонических плоских волн. Дисперсионное уравнение
  • § 27. Групповая скорость. Распространение узкополосного сигнала
  • § 28. Распространение широкополосного сигнала в диспергирующей среде
  • § 29. Пространственное спектральное разложение по плоским волнам
  • § 30. Поршневое излучение
  • § 31. Пристраивание плоской волны в среде к бегущейволне давления на плоскости
  • § 32. Неоднородные плоские волны
  • § 33. Пространственный спектр по плоским волнам для любого распределения давления на плоскости
  • § 34. Пространственный спектр по плоским волнам для любого распределения нормальных скоростей на плоскости
  • § 35. Волны, модулированные по фронту
  • § 36 Волны комплексных частот
  • ГЛАВА IV. ЭНЕРГИЯ ЗВУКОВЫХ ВОЛН
  • § 38. Плотность энергии в звуковой волне
  • § 39. Плотность потока мощности в звуковой волне
  • ГЛАВА V. ОТРАЖЕНИЕ И ПРОХОЖДЕНИЕ ПЛОСКИХ ВОЛН ПРИ НОРМАЛЬНОМ ПАДЕНИИ
  • § 40. Отражение и прохождение звука
  • § 41. Отражение от идеальных границ. Метод мнимых изображений
  • § 42. Правильное отражение. Отражение гармонических волн
  • § 43. Отражение и прохождение звука на границе двух сред
  • § 44. Плавное изменение свойств среды. Лучевая картина
  • § 45. Проводимость и импеданс линейного препятствия. Поле перед препятствием
  • § 46. Отражение от «сосредоточенной массы» и прохождение через нее
  • § 47. Отражение от «сосредоточенной упругости» и прохождение через нее
  • § 48. Отражение от резонатора. Согласование двух сред
  • § 49. Препятствия в виде плоскопараллельных слоев
  • § 50. Отражение негармонических волн
  • § 51. Теория длинных линий
  • § 52. Узкая труба и стержень как длинные линии
  • ГЛАВА VI. НАКЛОННОЕ ПАДЕНИЕ ПЛОСКИХ ВОЛН
  • § 53. Отражение и прохождение плоских волн при наклонном падении. Закон Снеллиуса
  • § 54. Отражение и прохождение звука на границе двух сред
  • § 55. Анализ формул Френеля
  • § 56. Отражение гармонических волн и импульса при закритических углах скольжения. Полное отражение
  • § 57. Рефракция лучей в неоднородной среде
  • § 58. Проводимость и импеданс при синусоидальном распределении давления по плоскости. Отражение от поверхности с заданной проводимостью. Учет, неидеальности среды
  • § 59. Поверхностная волна вблизи плоской границы, характеризуемой нормальной проводимостью
  • § 60. Применение теории длинных линий к задачам о наклонном падении волн
  • ГЛАВА VII. ВОЛНЫ В УЗКИХ ТРУБАХ
  • § 62. Гармонические волны в узкой трубе
  • § 63. Ограниченные трубы. Собственные колебания в ограниченных трубах
  • § 64. Труба, ограниченная крышками с конечной проводимостью
  • § 65. Крышки с потерями
  • § 66. Свободные колебания в трубах. Задачи с начальными условиями
  • § 67. Вынужденные колебания в трубах
  • § 68. Распространение звука в трубах с податливыми стенками
  • ГЛАВА VIII. ВОЛНОВОДЫ
  • § 69. Волноводное распространение звука
  • § 70. Нормальные волны. Плоская задача
  • § 71. Волноводы с идеальными стенками
  • § 72. Нормальная проводимость стенок
  • § 73. Поглощающие стенки
  • § 74. Создание гармонического поля в волноводе
  • § 75. «Затягивание» импульса в волноводе
  • § 76. Волновод с прямоугольным сечением
  • § 77. Стоячие волны в помещении
  • § 78. Произвольные свойства стенок
  • § 79. Распространение инфразвука в море. Плоская задача
  • § 80. Распространение инфразвука в море. Трехмерная задача
  • § 81. Круглая труба как волновод
  • ГЛАВА IX. СФЕРИЧЕСКИ-СИММЕТРИЧНЫЕ ВОЛНЫ
  • § 82. Сферические волны
  • § 83. Сферически-симметричные волны
  • § 84. Скорость частиц в сферически-симметричной волне
  • § 85. Гармонические сферически-симметричные волны
  • § 86. Сферически-симметричные колебания сферического объема жидкости
  • § 87. Монополь. Объемная скорость
  • § 88. Сопротивление среды в сферической волне. Присоединенная масса
  • § 89. Колебания упругой сферы в среде. Колебания газового пузырька в воде
  • § 90. Мощность излучения монополя. Плотность энергии в сферически-симметричной волне
  • § 91. Лучевая картина для монополя, Монополь в слоисто-неоднородной среде
  • § 92. Монопольный приемник
  • § 93. Совместная работа нескольких монополей
  • § 94. Характеристики направленности системы монополей
  • § 95. Приемные системы из монопольных приемников
  • § 96. Близкорасположенные монополи
  • § 97. Мощность, излучаемая при совместном действии близкорасположенных монополей
  • § 98. Монополь в волноводе
  • § 99. Взаимодействие монополей в волноводе
  • ГЛАВА X. ДИПОЛЬ
  • § 100. Диполь. Момент диполя
  • § 101. Диполь как осциллирующая сфера. Кардиоидный излучатель
  • § 102. Присоединенная масса диполя. Сила диполя
  • § 103. Влияние идеальных стенок на излучение диполя
  • § 104. Мощность излучения диполя
  • § 105. Негармонический дипольный источник
  • § 106. Осцилляции и излучение звука малым твердым телом под действием сторонней силы
  • § 107. Вращающийся диполь
  • § 108. Дипольное излучение малых тел, осциллирующих с большой амплитудой. Дипольное излучение вращающихся тел
  • ГЛАВА XI. РАССЕЯНИЕ ЗВУКА
  • § 109. Рассеяние звука на препятствии
  • § 110. Малое препятствие, отличающееся от среды только сжимаемостью
  • § 111. Малое препятствие, отличающееся от среды только плотностью
  • § 112. Рассеяние звука пузырьком газа в жидкости
  • § 113. Резонатор Гельмгольца. Рассеяние звука резонатором Гельмгольца
  • § 114. Рассеяние звука в слабо неоднородной среде
  • § 115. Рассеяние от слабо шероховатой поверхности
  • ГЛАВА XII. ПОГЛОЩЕНИЕ ЗВУКА
  • § 116. Затухание звука
  • § 117. Затухание звука в результате поглощения
  • § 118. Различные механизмы поглощения звука
  • § 119. Индикаторные диаграммы для частицы среды
  • § 120. Расчет коэффициентов поглощения звука для различных механизмов поглощения
  • ГЛАВА XIII. РАСПРОСТРАНЕНИЕ ВОЛН КОНЕЧНОЙ АМПЛИТУДЫ
  • § 121. Волны конечной амплитуды
  • § 122. Плоская бегущая волна конечной амплитуды (точное решение)
  • § 123. Нахождение квадратичной поправки методом малых возмущений
  • § 124. Квадратичная поправка в плоской волне
  • § 125. Квадратичная поправка для бегущей плоской волны
  • § 126. Нелинейное взаимодействие волн. Акустическое детектирование
  • § 127. Затухание волн конечной амплитуды, обусловленное нелинейностью
  • § 128. О нелинейных поправках высших порядков
  • § 129. Распространение плоской волны конечной амплитуды в среде с дисперсией скорости
  • § 130. Стоячие волны конечной амплитуды
  • § 131. Уравнения квадратичной поправки для неодномерных волн
  • § 132. О нелинейном взаимодействии плоских волн, бегущих под углом друг к другу
  • ГЛАВА XIV. УПРУГИЕ ВОЛНЫ В ТВЕРДЫХ ТЕЛАХ
  • § 133. Твердое тело как акустическая среда
  • § 134. Тензор деформации
  • § 135. Тензор напряжений
  • § 136. Закон Гука
  • § 137. Граничные условия для твердых тел
  • § 138. Однородные деформации. Различные модули упругости
  • § 139. Продольные и поперечные плоские волны в твердом теле
  • § 140. Общие уравнения распространения волн в твердом теле
  • § 141. Скалярный и векторный потенциалы
  • ГЛАВА XV. ОТРАЖЕНИЕ И ПРОХОЖДЕНИЕ ПЛОСКИХ ВОЛН В ТВЕРДОМ ТЕЛЕ. ТВЕРДЫЕ ВОЛНОВОДЫ
  • § 143. Отражение и прохождение звука на границе жидкости и твердой среды
  • § 144. Рэлеевская волна
  • § 145. Влияние граничащей среды на поверхностные волны
  • § 146. Твердые волноводы
  • ГЛАВА XVI. СФЕРИЧЕСКИЕ ВОЛНЫ В ТВЕРДОМ ТЕЛЕ
  • § 147. Типы сферических волн в твердом теле
  • § 148. Сферически-симметричные волны. Радиальные колебания твердой сферы
  • § 149. Монополь в твердой среде
  • § 150. Колебания сферической полости в твердом теле. Рассеяние на резонансной полости
  • § 151. Крутоль
  • § 152. Диполь в твердом теле
Источник

Государственная
система санитарно-эпидемиологического
нормирования Российской Федерации

4.3. МЕТОДЫ КОНТРОЛЯ. ФИЗИЧЕСКИЕ ФАКТОРЫ

Определение плотности потока мощности
электромагнитного поля в местах размещения
радиосредств, работающих в диапазоне частот
700 МГц – 30 ГГц

Методические указания

МУК 4.3.043-96

Госкомсанэпиднадзор России

Москва

1996

1. Разработаны сотрудниками Самарского
отраслевого научно-исследовательского института радио Министерства связи
Российской Федерации (Бузовым А. Л., Романовым В. А.) и Поволжского института
информатики, радиотехники и связи (Кубановым В. П., Сподобаевым Ю. М.).

2. Утверждены и введены в действие
Председателем Госкомсанэпиднадзора России – Главным Государственным санитарным
врачом Российской Федерации 2 февраля 1996 г.

3. Представлены Министерством связи России (№
6109 от 23.11.95).

4. Введены впервые.

СОДЕРЖАНИЕ

1.
Область применения

2. Сущность
метода

3. Краткая
характеристика источников излучения

4.
Методика расчета плотности потока мощности апертурных антенн

5.
Порядок расчета плотности потока мощности в произвольной точке горизонтальной
плоскости

6. Примеры
расчета

7.
Инструментальный контроль уровней электромагнитных полей технических средств
РРСП ПВ, ТРРСП и ССП

Список
сокращений и обозначений

“УТВЕРЖДАЮ”

Председатель
Государственного комитета санитарно-эпидемиологического надзора Российской
Федерации – Главный Государственный санитарный врач Российской Федерации

Е.Н. Беляев

2
февраля 1996 года

МУК 4.3.043-96

Дата
введения: с момента утверждения.

4.3. МЕТОДЫ КОНТРОЛЯ. ФИЗИЧЕСКИЕ ФАКТОРЫ

Определение плотности потока мощности
электромагнитного поля в местах размещения
радиосредств, работающих в диапазоне частот
700 МГц – 30 ГГц

Методические указания

1. Область применения

Методические указания составлены в помощь
инженерам органов и учреждений санитарно-эпидемиологической службы,
инженерно-техническим работникам, проектным организациям средств связи с целью
обеспечения предупредительного санитарного надзора за источниками излучения технических
средств радиорелейных систем прямой видимости (РРСП ПВ), тропосферных
радиорелейных систем (ТРРСП) и спутниковых систем (ССП) радиовещания,
телевидения и радиосвязи диапазона частот 700 МГц – 30 ГГц, определения границ
санитарно-защитных зон и зон ограничения застройки, а также для прогнозирования
уровней электромагнитного поля (ЭМП) при выборе мест размещения этих средств.

2. Сущность метода

Названные
системы предназначены для передачи различных сообщений и работают, как правило,
в непрерывном режиме. Конструкции антенн довольно разнообразные, но практически
все они относятся к классу апертурных. Все апертурные антенны имеют
многолепестковые диаграммы направленности (ДН), что определяет сложную
структуру электромагнитного поля (ЭМП) вблизи радиотехнических объектов (РТО).

Методика
расчетного прогнозирования электромагнитных полей вблизи технических средств
радиорелейных и спутниковых систем передачи базируется на строгих решениях
соответствующих электродинамических задач. Основные положения методики и
расчетные формулы приведены в разделе
4.

Методические
указания содержат методику расчетного прогнозирования плотности потока мощности
электромагнитного поля излучающих технических средств радиосвязи, радиовещания
и телевидения в диапазоне частот 700 МГц-30 ГТц, а также методику измерений
уровней электромагнитного поля.

3. Краткая характеристика
источников излучения

3.1. Некоторые
частотные и энергетические характеристики типового оборудования, а также
геометрические и электрические параметры антенн РРСП ПВ приведены в табл. 3.1.

3.2. В табл. 3.1 использованы общепринятые
обозначения антенн: РПА – рупорно-параболическая антенна: АДЭ – антенна
двухзеркальная с эллиптическим переизлучателем (число после аббревиатуры-
диаметр апертуры в метрах); ПАС – перископическая антенная система; ПА –
параболическая антенна.

3.3. Антенну
РПА можно рассматривать как квадратную апертуру с размерами 2,7 ´2,7
м2.

Антенна АДЭ имеет несколько модификаций,
отличающихся диаметром и углом раскрыва основного зеркала: АДЭ-5, АДЭ-3,5 и
АДЭ-2,5.

У основной
модификации ПАС апертуру верхнего зеркала можно считать кругом с диаметром 3,9
м.

3.4. Некоторые
частотные и энергетические характеристики типового оборудования, а также
геометрические и электрические параметры антенн ТРРСП приведены в табл. 3.2.

3.5. Некоторые
частотные и энергетические характеристики типового оборудования земных станций
ССП, а также геометрические и электрические параметры их антенн приведены в табл. 3.3.

3.6. Антенны
РРСП ПВ, ТРРСП и ССП по принципу действия рассматриваются как излучающие
отверстия (апертуры) круглой или квадратной формы. Площадь апертуры существенно
превышает квадрат длины волны излучаемого ЭМП.

Таблица 3.1

Характеристика
типового оборудования РРСП ПВ

№ №
п.п.

Тип
РРСП

Средняя длина волны, см

Мощность передатчика одного
ствола, Вт

Тип антенны

Диаметр апертуры
м

Коэфф. усилен
дБ

1.

Рассвет-2

8,2

5

РПА

–

39,5

2.

Восход

8,2

10

РПА

–

39,9

3.

Курс-2м

15,8

1,6

АДЭ-5

5

37,9

4.

Курс-4

8.2

0,5

РПА

–

39,5

АДЭ-5

5

43,5

АДЭ-3,5

3,5

40,7

ПАС

3,9

40

5.

Курс-6

5,07

7,5

РПА

–

43

АДЭ-3,5

3,5

44,8

ПАС

3,9

40

6.

Курс-8

3,7

0,4

АДЭ-2,5

2,5

44

ПАС

3,9

43

7.

Радуга-4

8,2

4

РПА

–

39,5

АДЭ-5

5

43,5

АДЭ-3,5

3,5

40,7

ПАС

3,9

40

8.

Радуга-6

5,07

3

РПА

–

43

АДЭ-3,5

3,5

44,8

ПАС

3,9

40

9.

Ракита-8

3,7

0,6

АДЭ-2,5

2,5

44

ПАС

3,9

43

10.

Радан

2,7

0,1

ПА

1,5

45

11.

Комплекс-5М

2,7

0,5

ПА

1,5

45

Таблица 3.2

Характеристика типового оборудования ТРРСП

№ №
п.п.

Тип
ТРРСП

Средняя длина волны, см

Мощность,
Вт
и число передат.

Тип антенны

Размер апертуры
м

Коэфф. усилен
дБ

1.

Горизонт-М

30

3 ´ 103 ´ 2

НПА

20 ´ 20

43

2.

ТР-120

30

5 ´ 103 ´ 2

30 ´ 30

47

3.

ДТР-12

30

104 ´ 2

Примечание:
В таблице 3.2. использовано обозначение: НПА – несимметричная параболическая
антенна.

Таблица 3.3

Характеристика типового оборудования ССП

№ №
п.п.

Тип
ССП

Средняя длина
волны

Мощность передатчика одного
ствола, Вт

Тип антенны

Диаметр апертуры
м

Коэфф. усилен
дБ

1.

Орбита-2

5

104

2-х
зерк.

12

52

2.

Марс

5

3 ´ 103

Кассегрена

7

50

3.7. Данные, приведенные в табл. 3.1 ¼ 3.3,
не следует считать исчерпывающими и неизменными. Излагаемая ниже методика
оценки ППМ позволяет легко справиться с задачей, если даже речь будет идти об
апертурной антенне иной конструкции.

4. Методика расчета ППМ апертурных
антенн

4.1. Плотность
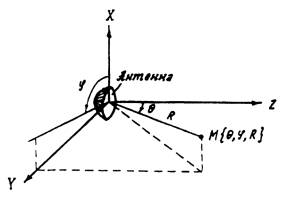
потока мощности, создаваемая апертурной антенной в расчетной точке ( рис. 1) определяется по формуле:

П = ПА + ПОбл,
Вт/м2                                                 (4.1)

Рис. 1. Взаимное
расположение антенны и точки наблюдения

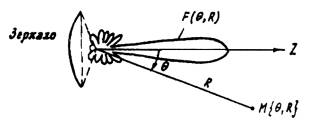
Рис. 2. К расчету
составляющей ППМ – ПА

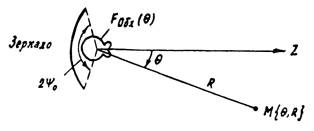
Рис. 3. К расчету
составляющей ППМ – ПОбл

где, ПА
– апертурная составляющая ППМ ( рис. 2):

ПОбл
– составляющая ППМ, определяемая непосредственно излучением облучателя ( рис. 3).

4.2. В предположении
осевой симметрии ХН облучателя и антенны ППМ не зависит от координаты j. При
этом составлявшие ПА и ПОбл записываются в виде

, Вт/м2                                               ( 4.2)

, Вт/м2                                         ( 4.3)

где, Р –
мощность, излучаемая антенной, Вт;

D0 – КНД антенны в
направлении максимального излучения в волновой зоне (величина безразмерная);

В2( R) – функция, учитывающая
изменение КНД по мере перехода расчетной точки из ближней зоны в волновую
(величина безразмерная);

 – нормированная ХН
антенны по мощности (величина безразмерная);

 – КНД облучателя в
направлении его максимального излучения (величина безразмерная);

 – нормированная ХН
облучателя по мощности (величина безразмерная);

 – сферические
координата расчетной точки.

Существенно
отметить, что КНД и ХН апертуры являются функциями расстояния R, а эти же параметры облучателя не
зависят от R, т.к.
расчетная точка по отношению к облучателю всегда находится в волновой зоне.

4.3. Закон
распределения амплитуды поля по апертуре принят в виде:

– для круглой
апертуры

                                                         ( 4.4)

– для квадратной апертуры

                                                             ( 4.5)

где, a =
0,316;

r – текущее значение
координаты на диаметре апертуры;

t –
текущее значение координата вдоль любой стороны квадрата;

 – сторона квадрата.

4.4. Вне углов
сектора перехвата энергии облучателя зеркалом функция , считается неизменной и равной 0,316. Следовательно в этом
случае  = 0,1.

С учетом этого
формула (4.3) записывается в таком
виде:

, Вт/м2                                                                                     ( 4.6)

4.5. Методика
расчета ХН антенны предполагает использование переменных и u и x, которые записываются в виде:

– для круглой апертуры,

– для квадратной апертуры,                                                   (4.7)

x = R/Rгр                                                                                                              ( 4.8)

где d диаметр апертуры, м;

 – длина волны, м;

 – для круглой
апертуры;                                                             ( 4.9)

 -для квадратной
апертуры.                                                         ( 4.10)

Переменные u и x принято называть обобщенными
координатами. Величину x
часто называют относительным расстоянием.

4.6. С учетом
введения обобщенных координат u и x формула (4.2)
приводится к виду

, Вт/м2                                                           ( 4.11)

4.7. Перевод
размерности ППМ Вт/м2 в мкВт/см2 осуществляется
умножением выражений ( 4.6) и ( 4.11) на 100.

4.8. Переход
от абсолютных значений размерности ППМ к относительным (децибелам относительно
1 мкВт/см2) позволяет записать выражения ( 4.6) и ( 4.11)
в виде:

, дБ                          ( 4.12)

,                                                                   ( 4.13)

где, В(х) –
функция, учитывающая изменение КНД в зависи мости от относительного расстояния;

 – нормированная ХН в координатах u, x.

Прочие величины, входящие в ( 4.12) и ( 4.13)
определены выше.

Формула ( 4.12)
справедлива как для круглой апертуры, так и для квадратной. В случае ее
применения для квадратной апертуры в знаменателе первого слагаемого параметр d (диаметр) заменяется на  (сторона квадрата).

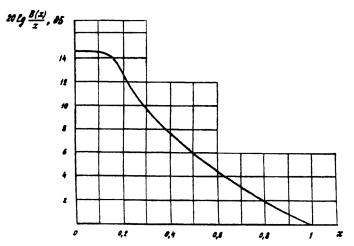
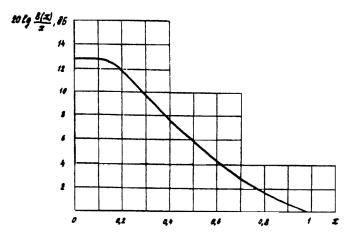
4.9. Функция  в области х < 0,2 является осциллирующей. При х > 0,2 она изменяется монотонно. В силу
специфики задачи оценки ЭМО осциллирующая часть функции заменяется огибающей ее
максимумов. На рис. 4 и рис. 5 приведена эта функция соответственно для антенн с
круглой и квадратной апертурами. В области х > 1

.

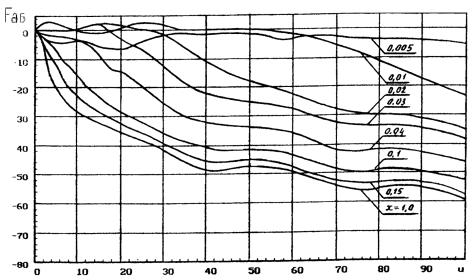
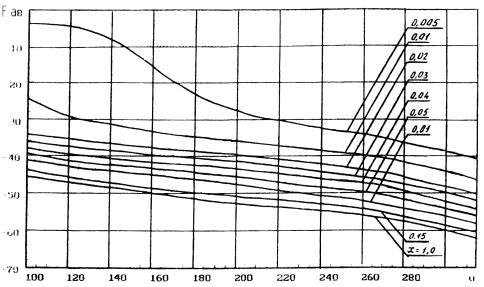
4.10. Функция  сильно осциллирующая. Графики гарантированных
огибающих ХН антенн с круглой апертурой для фиксированных значений х
приведены на рис. 6 и рис. 7. По оси ординат отложены значения F дБ =   дБ.

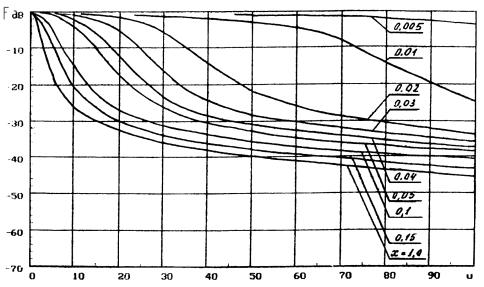
Аналогичные кривые для антенн с квадратной
апертурой приведены на рис. 8 и рис. 9.

4.11. Функция  рассчитывалась апертурным методом – численным
интегрированием полей элементарных излучателей (элементов Гюйгенса),
расположенных по всей апертуре. В случае круглой апертуры учитывалось затенение
апертуры облучателем. Учет затенения осуществлялся исключением интегрирования
полей элементов Гюйгенса, расположенных в центре апертуры внутри круга с
диаметром dr . В методике принято, что коэффициент затенения dr / d = 0,1 ( dr – диаметр “теневого диска”, d – диаметр апертуры).

4.12. Графики
гарантированной огибающей для различных х, приведенные на рис. 6 ¼ 9, являются
универсальными, т.е. они справедливы для апертур любых размеров при условии,
что линейные размеры антенны существенно превышают длину волны.

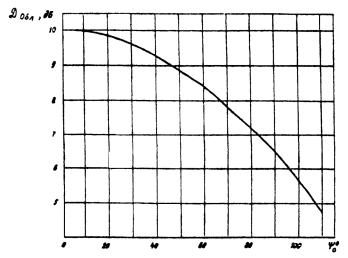
4.13. Величина D Обл , дБ = 10 lg D Обл определяется ХН облучателя. По выбранному
закону распределения поля по апертуре ( 4.4)
или ( 4.5), используя геометрические
характеристики зеркала d и y 0 , можно записать аналитическое выражение   в секторе углов перехвата энергии зеркалом.
Вне этого сектора  = const = 0,316. График зависимости   приведен на рис.
10.

Рис. 4. График функции  для круглой апертуры

Рис. 5. График функции  для квадратной
апертуры

Рис. 6. Гарантированные огибающие XH круглой апертуры с учетом затенения для u = 0 ¼ 100

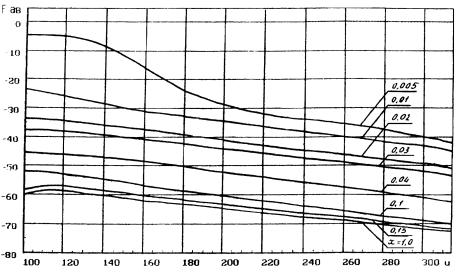
Рис. 7. Гарантированные огибающие XH круглой апертуры с учетом затенения для u = 100 ¼ 314

Рис. 8. Гарантированные огибающие XH квадратной апертуры для u = 0 ¼ 100

Рис. 9. Гарантированные огибающие XH квадратной апертуры для u = 100 ¼ 314

Рис. 10. Зависимость КНД облучателя в направлении максимального
излучения от угла

4.14. Термины
“облучатель”, “ХН облучателя”, “КНД облучателя” в
методике применяется как собственно к облучателю в однозеркальных ПА, так и к
системе “облучатель – вспомогательное зеркало” в двухзеркальных
антеннах.

4.15.
Ограничение по минимальному удалению расчетной точки от центра апертуры
определяется относительным расстоянием х = 0,005.

4.16. Ограничение по сектору углов, в котором
методика дает возможность расчета ППМ, определяется :

– при   ³
90° сектор составляет от 0° до ±90°;

– при   <
90° сектор составляет от 0° до ±(180° – ).

Вне этих
секторов в рассматриваемых задачах ППМ считается пренебрежимо малой.

4.17.
Дифракционные явления, на кромках зеркала и вспомогательных конструкциях
антенны не учитываются.

4.18. Расчет
суммарной ППМ осуществляется по формуле:

,                                                           ( 4.14)

где, ПА,дБ  и ПОбл,дБ вычисляются по формулам (4.12) и ( 4.13).

4.19. При
расчетах ЭМО вблизи радиотехнических объектов, в составе которых несколько,
антенн, в выбранных точках рассчитывается ППМ от каждой антенны, а полная ППМ
находится суммированием ППМ. создаваемых отдельными антеннами.

5. Порядок расчета ППМ в произвольной
точке горизонтальной плоскости

5.1.
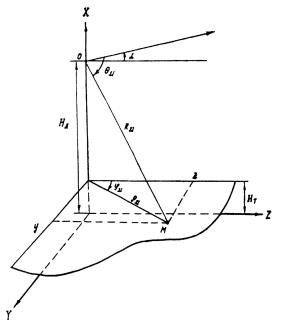
Постановка задачи иллюстрируется рис. 11.
Центр апертуры – 0, его высота над землей – НА. Угол a
характеризует отклонение направлений максимального излучения от плоскости
горизонта. Ось Z
системы координат XYZ
совмещается с проекцией направления максимального излучения на плоскость Y0 Z. Горизонтальная плоскость, на которой
определяется ППМ, находится на высоте Нт над землей. Расчетная точка
задается либо через координаты rМ (расстояние до точки М вдоль поверхности
земли) и jМ
(азимут), либо через y
и z.

Заданными
считаются:

Р – мощность,
излучаемая антенной, вт;

l – длина волны, м;

d или а – диаметр или
сторона квадрата апертуры, м;

D0 – КНД антенны в
направлении максимального излучения в волновой зоне;

2 y0
– угол раскрыва антенны.

Если какие-либо
из перечисленных параметров для реальной антенны неизвестны, их, как правило,
можно рассчитать, используя соответствующую литературу по антенно-фидерным
устройствам.

Рис.
11. К расчету ППМ в произвольной точке

5.2. Порядок
расчета следующий:

5.2.1.
Вычисляется расстояние “центр апертуры – точка наблюдения”:

.                                                                      (5.1)

5.2.2.
Вычисляется угол между направлением максимального излучения и направлением
линии “центр апертуры – точка М”:

                                        (5.2)

5.2.3. По формулам
(4.9) или ( 4.10) определяется
граничное расстояние R гр .

5.2.4.
Определяются параметры uм
и xм
по формулам (4.7) и ( 4.8) соответственно.

5.2.5. По
графикам рис. 4 или рис. 5 находится значение функции  в дБ. x

5.2.6. По
графикам рис. 6 ¼ 9 находится значение F ( uм,
хм) в дБ.

5.2.7.
Применение формулы (4.12) позволяет
получить значение ППМ антенны ПА в дБ.

5.2.8. По графику рис. 4.10 определяется значение D Обл , в дБ.

5.2.9.
Применение формулы (4.13) позволяет
получить значение ППМ облучателя ПОбл в дБ.

5.2.10.
суммарное значение ППМ рассчитывается по формуле (4.14).

5.2.11.
Повторяя операции по п. п. 5.2.1 ¼
5.2.10 последовательно для различных
точек выбранного азимута ( jм= const), можно определить, во-первых, как меняется ППМ вдоль
соответствующего азимута, а, во-вторых, найти ту точку, где ППМ равна ПДУ. Если
подобные точки найти на других азимутальных линиях, проведенных, например,
через 10°, то геометрическое место таких точек будет границей соответствующей
санитарной зоны (СЗЗ или ЗОЗ).

6. Примеры расчета

Пример 1

6.1. Постановка задачи.

Техническое
средство – оборудование РРСП ПВ “Радуга-4” на оконечной радиорелейной
станции. Работают три радиоствола. Используется антенна АДЭ-5 с углом раскрыва
зеркала 2 y0
= 210°. Антенна находится на высоте 50 м.

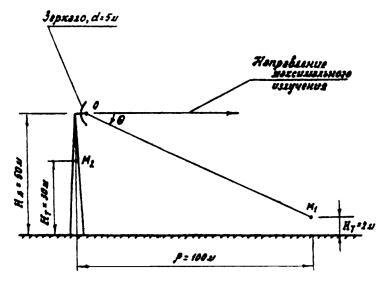
Сравнить ППМ в точках М1, и М2
ПДУ ППМ. Точка М1 расположена в направлении на соседнюю станцию, ее
высота над поверхностью земли – 2м. а удаление от основания мачты – 100 м.
Точка М2 расположена на оси мачты, на высоте 30 м. Постановка задачи
иллюстрируется рис. 12.

6.2. Порядок решения.

6.2.1. По табл. 3.1 определяются:

– суммарная
мощность, излучаемая антенной, Р = 3 ´4 = 12 Вт (работают 3 ствола, кпд АФТ считается
равным 1);

– длина волны lср
= 0,082м;

– диаметр
антенны d = 5 м;

– КНД антенны АДЭ-5 D 0,дБ = 43,5 дБ.

6.2.2. Расчет ППМ выполняется сначала в точке
М1, затем в точке М2.

Расчет ППМ в точке М1

6.2.3.
Находится расстояние Rм
– “центр апертуры – точка М1” и угол Qм:

 м;

.

При j = 0
и a
= 0:

.

Рис. 12. Иллюстрация к примеру расчета ППМ от
антенны РРСП ПВ

6.2.4. Находится граничное расстояние R гр :

R гр = 2 d 2 / l = 2 ´ 52 / 0,082 = 610 м.

6.2.5 Определяются координаты x и u :

x = R м / R гр = 111/610 = 0,182,

.

6.2.6. По графикам рис. 6 определяется функция

20lgF(u,
x) = – 55 дБ

6.2.7. По графику рис. 4 определяется функция

 дБ.

6.2.8. По формуле
(4.12) рассчитывается ПА:

 
дБ.

6.2.9.
По графику рис. 10 определяем

D Обл , дБ = 10 lg D Обл = 5 дБ.

6.2.10. По формуле (4.13) рассчитывается ПОбл:

 дБ.

6.2.11. По формуле
(4.14) рассчитывается суммарная ППМ в точке М1:

 
 мкВт/см2.

Вывод: ППМ в точке М1 существенно
меньше ПДУ = 10 мкВт/см2.

Расчет ППМ в точке М2

6.2.12. Принимается, что R М » НА – НТ = 50 – 30 + 20 м.

Q М = 90 ° .

6.2.13. Определяются

R гр = 2 d 2 / l = 2 ´ 52 / 0,082 = 610 м,

x = R м / R гр = 20/610 = 0,032,

.

6.2.14. По графикам рис. 7 определяется функция

20lgF(u,
x) = – 42 дБ .

6.2.15. По графику рис. 4 определяется функция

 дБ.

6.2.16. По формуле (4.12) рассчитывается ПА:

ПА = -38,9 + 43,5 + 14,5 – 42 + 3
= -19,9 дБ.

6.2.17. По формуле (4.13)
рассчитывается ПОбл с учетом того, что величина D Обл, дБ определена в п. 6.2.9.:

 дБ.

6.2.18. По формуле (4.14) рассчитывается суммарная ППМ в точке
М2:

П = 10-1,99 +10-1,12 =
0,086 мкВт/см2.

Вывод: ППМ в
точке М2 существенно меньше ПДУ = 10 мкВт/см2.

Пример 2

6.3. Постановка задачи.

Техническое
средство – оборудование ТРРСП ТР-120 на оконечной станции. Используются две
антенны НПА 30 ´30
м2. Разнос между антеннами 40 м, центры апертур антенн находятся на
высоте НА = 25 м над землей.

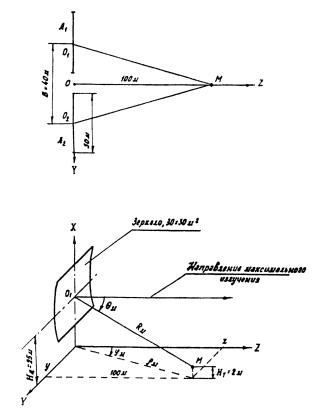
Оценить ППМ в точке М, которая расположена в
направлении на соседнюю станцию, а ее высота над землей – 2 м. Удаление точки М
от линии проекции антенн на поверхность земли 100 м. Постановка задачи
иллюстрируется рис. 13.

6.4. Порядок решения.

6.4.1. По
табл. 2.2 определяются

– мощность,
излучаемая одной антенной, Р = 5 кВт = 5000 Вт (при кпд АФТ равном 1);

– длина волны lср
= 0,3 м;

– размеры антенны а ´ а = 30 ´ 30 м2;

– КНД антенны D 0, дБ = 47 дБ.

Расчет ППМ выполняется сначала для одной
антенны затем для другой. Результата расчетов ППМ суммируются.

Рис. 13. Иллюстрации к примеру расчета ППМ от антенн ТРРСП

Расчет ППМ,
создаваемой антенной А1 в точке М

6.4.2.
Находится расстояние Rм
и угол Qм:

   
 м;

.

Для = 0, ,

 м

.

6.4.3. Находится граничное расстояние R гр :

R гр = 2 а2/ l = 2 ´ 302 / 0,3 = 6000 м.

6.4.4. Определяются координаты х и u :

x = R м / R гр = 104,5/6000 = 0,017,

.

6.4.5. По графику рис. 5 определяется функция

 дБ.

6.4.6. По
графикам рис. 8 определяется функция

20lgF(u,
x) = – 26 дБ .

6.4.7. По формуле (4.12) рассчитывается ПА:

,
 дБ.

6.4.8. Угол раскрыва зеркала антенны с
размерами 30 ´ 30 м2 2 y 0 равен 40°. По графику рис. 10
определяется D Обл,
дБ :

D Обл , дБ = 10 lg D Обл = 9,8 дБ.

6.4.9. По формуле
(4.13) рассчитывается ПОбл:

 дБ.

6.4.10. По формуле (4.14) рассчитывается ППМ,
создаваемая в точке М антенной А1 – П1:

 2,5 + 3,5 = 6 мкВт/см2.

Расчет ППМ, создаваемой антенной А2 в точке М

6.4.11. В силу
симметрии расположения точки М относительно антенн А1 и А2
ППМ, создаваемая антенной А2 в точке М, будет равна ППМ, создаваемой
в этой точке антенной А1, т.е.
П1 = П2 = 6 мкВт/см2.

Суммарная ППМ в точке М от совокупности
антенн А1 и А2 будет равна

П = П1 +П2 = 6 + 6 = 12
мкВт/см2.

Вывод: ППМ в точке М превышает ПДУ (П > 10 мкВт/см2).

Пример 3

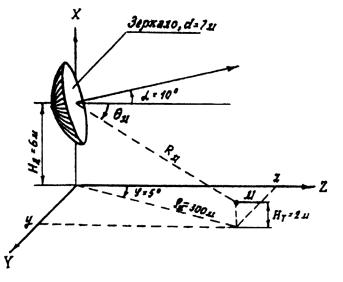
6.5. Постановка задачи.

Техническое
средство – ССП. Передатчик работает на длине волны l = 0,05 м. Мощность
передатчика Р = 3 кВт. Используется антенна Кассегрена с углом раскрыва 2 y0
= 180° и D0 =
50 дБ. Диаметр апертуры d
= 7 м. Высота центра апертуры над землей НА = 6 м. Направление
максимального излучения составляет с плоскостью горизонта угол a =
10°. Постановка задачи иллюстрируется рис. 14.

6.6. Порядок решения.

6.6.1. Находится расстояние R м и угол q м :

 м;

  .

6.6.2. Находится граничное расстояние R гр :

R гр = 2 d 2 / l = 2 ´ 72 / 0,05 = 1960 м.

6.6.3. Определяются координаты х и u :

x = R м / R гр = 300/1960 = 0,153,

.

6.6.4. По графику рис. 4 определяется функция

20 lg [В( x )/х] = 14,5 дБ.

6.6.5. По
графикам рис. 6 определяется функция 20 lgF ( u , x )
= – 54 дБ.

6.6.6. По формуле (4.12) рассчитывается ПА:

,
 дБ.

6.6.7. По графику рис. 10 определяется D Обл, дБ :

D Обл , дБ = 10 lg D Обл = 6,5 дБ.

6.6.8. По формуле
(4.13) рассчитывается ПОбл:

 дБ.

6.6.9. По формуле (4.14) рассчитывается суммарная ППМ, в точке
М:

 0,07 + 0,12 = 0,19
мкВт/см2.

Вывод: ППМ в точке М существенно меньше ПДУ =
10 мкВт/см2.

Рис. 14. Иллюстрация к примеру расчета ППМ от антенны ССП

7. Инструментальный контроль
уровней электромагнитных полей технических средств РРСП ПВ, ТРРСП и ССП

Инструментальный
контроль уровней ЭМП проводится с целью определения фактического состояния
электромагнитной обстановки в районах размещения излучающих средств и служит
средством оценки достоверности результатов расчета.

Измерения
проводятся:

– на этапе
предупредительного санитарного надзора- при приемке радиотехнического объекта
(РТО) в эксплуатацию;

– на этапе
текущего санитарного надзора- при изменении технических характеристик или
режимов работы (мощности излучения, антенно-фидерного тракта, направлений
излучения и т.п.);

– при
изменении ситуационных условий размещения станций (изменение расположения
антенн, высот их установки, азимута или угла места максимального излучения,
застройки прилегающих территорий);

– после
проведения защитных мероприятий, направленных на снижение уровней ЭМП;

– в порядке плановых контрольных измерений
(не реже одного раза в год).

7. 1. Подготовка к
проведению измерений

При подготовке
к проведению измерений проводятся следующие работы:

– согласование
с заинтересованными предприятиями и ор ганизациями
цели, времени и условий проведения измерений;

–
рекогносцировка района проведения измерений;

– выбор трасс
(маршрутов) и площадок измерений, при этом, число трасс определяется рельефом
местности, прилегающей к объекту, и целью измерений;

– организация связи для обеспечения
взаимодействия между персоналом станции и группой измерений;

– обеспечение измерений дальности до точки
измерений;

– определение необходимости использования
средств индивидуальной защиты;

– подготовка необходимой измерительной
аппаратуры.

7.2. Выбор трасс (маршрутов) измерений

Число трасс
определяется рельефом прилегающей местности и целью измерений. При установлении
границ СЗЗ выбирается несколько трасс, определяемых по конфигурации
теоретических границ СЗЗ и прилегающей селитебной зоны. При текущем санитарном
надзоре, когда характеристики станции и условия ее эксплуатации остаются
неизменными, измерения могут проводиться по одной характерной трассе или по
границе СЗЗ.

При выборе
трасс учитывается характер прилегающей местности (рельеф, растительный покров,
застройка и пр.), в соответствии с которым, район, прилегающий к станции,
разбивается на секторы. В каждом секторе выбирается радиальная, относительно
станции, трасса. К трассе предъявляются требования:

– трасса
должна быть открытой, а площадки, на которых намечается поведение измерений,
должны иметь прямую видимость на антенну излучающего средства;

– вдоль
трассы, в пределах главного лепестка ХН, не должно быть переизлучателей
(металлических конструкций и сооружений, линий электропередачи и т.п.) И других
затеняющих местных предметов;

– наклон
трассы должен быть минимальным по сравнению с наклоном всех возможных трасс в
данном секторе;

– трасса
должна быть доступной для пешего передвижения или для автотранспорта;

–
протяженность трассы определяется на основе расчетного удаления границ СЗЗ и
глубины зоны ограничения застройки (в 1,5 – 2 раза больше);

– точки
(площадки) для проведения измерений следует выбирать с интервалом не более 25 м
– при удалении до 200-300 м от излучающей антенны; 50-100 м – при удалении от
200-300 м до 500-1000 м; 100 м и более – при удалении более 1000 м.

При выборе
площадок для проведения измерений следует учесть, чтобы в радиусе до 10 м
отсутствовали местные предметы и из любой ее точки обеспечивалась прямая
видимость на излучающую антенну.

7.3. Проведение
измерений

Для
инструментального контроля используются измерители плотности потока мощности
типа П3-9, П3-18 и им подобные. Измерительные комплекты должны быть исправны и
иметь действующее свидетельство о поверке.

Учитывая, что
санитарные зоны технических средств РРСП ПВ, ТРРСП и ССП находятся в ближнем электромагнитном поле антенн (зона
Френеля) и распределение плотности потока мощности имеет выраженный
осциллирующий характер, т.е. не является однородным, для измерения уровней
желательно использование измерительных антенн с наименьшей эффективной
поверхностью Sэфф.

Развертывание
и подготовка приборов к работе производится согласно инструкции по их
эксплуатации.

Выбор мест
измерений определяется необходимостью исключить облучение населения в местах его
возможного нахождения как в пределах санитарно-защитной зоны и зоны
ограничения, так и вне их.

В практике
санитарного надзора часто приходится приводить натурные измерения (оценку
электромагнитной обстановки) в служебной зоне, примыкающей к РТО, в том числе
внутри зданий и жилых помещений. В этом случае дело осложняется тем, что
измерения должны проводится как на открытой территории в дальней и ближней
зонах излучения, так и на закрытой, т.е. в зданиях, в жилых помещениях, где
пространство ограничено. При этом измерения проводятся в ближней зоне вторичных
источников излучения. Вторичными источниками излучения обычно являются
металлические, металлизированные и металлосодержащие конструкции и сооружения.
Интенсивность вторичного излучения может быть существенно выше интенсивности
прямой волны. Поэтому измерения проводятся как в местах, находящихся в прямой
видимости от антенны РТО, так и в области радиотени.

В обязательном
порядке обследованию, в границах санитарных зон, подлежат здания первой линии
относительно РТО. В случае превышения ПДУ проверке подвергаются строения
последующих линий, особенно строения, высота которых превышает высоту строений
первой линии. Для каждого переизлучателя, находящегося вне помещения,
рекомендуется определять границу, на которой уровень ЭМП не превышает ПДУ.

При
определении уровней ЭМП в помещениях измерения производятся у всех
переизлучающих предметов – у окон, у входной двери, в центре комнаты, на
балконе, начиная с минимально возможной высоты, определяемой возможностями прибора,
до высоты 2 м. При этом, расстояние до переизлучающих предметов должно быть не
менее 0.5м.

В каждой точке
контроля производится не менее трех измерений. Результатом является среднее
арифметическое значение этих измерений.

В каждой точке
измерений находится максимальный уровень плотности потока мощности по высоте до
2 м, при этом необходимо, учитывая положение фронта волны, производить
ориентацию измерительной антенны на максимум принимаемого сигнала.

При измерении
ППМ и обработке данных от нескольких антенн излучающего объекта необходимо
руководствоваться требованиями действующих санитарных норм.

Для измерения
дальности от центра антенны могут использоваться ситуационный план местности,
мерная лента, теодолит и другие доступные средства, обеспечивающие достаточную
точность.

По результатам
измерений составляется протокол. Результаты заносятся в санитарный паспорт
объекта и служат основанием для уточнения расчётных, границ санитарных зон.

СПИСОК СОКРАЩЕНИЙ И ОБОЗНАЧЕНИЙ

АДЭ –        антенна двухзеркальная с эллиптическим
переизлучателем

АФТ –
       антенно-фидерный тракт

ДН –           диаграмма направленности

ЗОЗ –         зона ограничения застройки

ИСЗ –        искусственный спутник Земли

КНД –        коэффициент направленного действия

НПА –        несимметричная параболическая антенна

ПА –           параболическая антенна

ПАС –        перископическая антенная система

ПДУ –        предельно-допустимый уровень

ППМ –       плотность потока модности

РПА –        рупорно-параболическая антенна

РРСП ПВ
– радиорелейная система передачи прямой видимости

РТО –        радиотехнический объект

СЗЗ –         санитарно защитная зона

ССП –        спутниковая система передачи

ТРРСП –
  тропосферная радиорелейная система
передачи

ХН –           характеристика направленности

ЭМО –       электромагнитная обстановка

ЭМП –       электромагнитное поле

Источник

Добавить комментарий