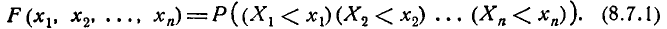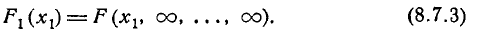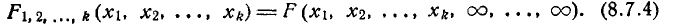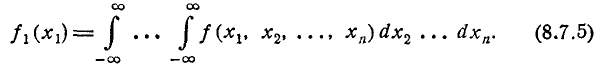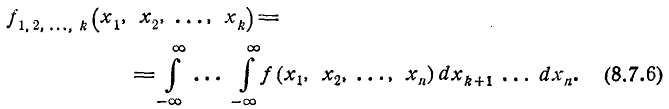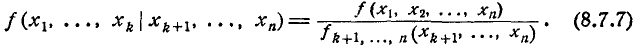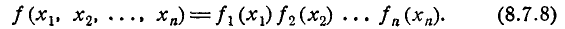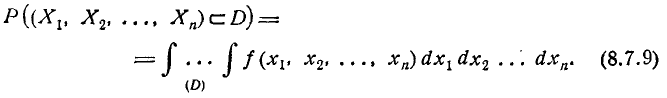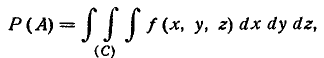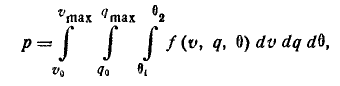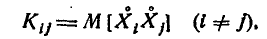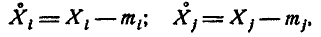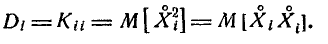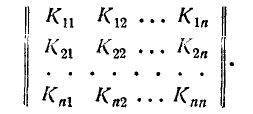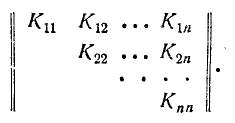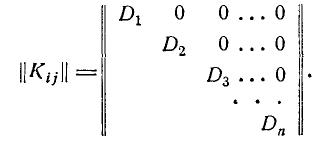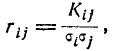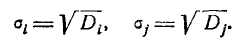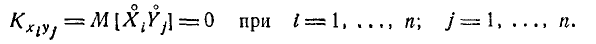Предположим, что
функция распределения
непрерывна и дважды дифференцируема,
тогда смешанную частную производную
функцииобозначим через
:
.
Функция
называется
плотностью распределения
системы непрерывных случайных величин
.
Зная плотность распределения,
можем определить вероятность попадания
случайной точкив произвольную область
:
. (5.1)
Используя формулу
(5.1), выразим функцию распределения
системы
через плотность распределения
:
. (5.2)
Рассмотрим свойства
плотности распределения системы двух
случайных величин.
Свойство 1.
Плотность распределения есть функция
неотрицательная:
.
Свойство 2.
Двойной несобствнный интеграл с
бесконечными пределами от плотности
распределения системы равен единице:
.
Пример 1.
Плотность распределения системы двух
случайных величин
задана выражением
.
Найти
.
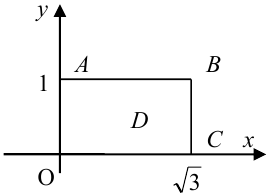
Определить функцию распределенияи найти вероятность попадания случайной
точки в прямоугольник с вершинами,
,
и
.
Решение. Пользуясь
свойством 2 плотности распределения,
найдем постоянную величину
:
.
Следовательно,
.
Функцию распределенияопределяем по формуле (5.2):
.
Вероятность
попадания случайной точки
в заданный прямоугольник согласно
формуле (5.1) равна
5. Условные законы
распределения.
Пусть известна
плотность распределения системы двух
случайных величин. Используя свойства
функций распределения, можно вывести
формулы для нахождения плотности
распределения одной величины, входящей
в систему:
. (5.3)
Перейдем теперь
к решению обратной задачи: по известным
законам распределения отдельных величин,
входящих в систему, найти закон
распределения системы. Как легко видеть,
в общем случае эта задача неразрешима.
Действительно, законы распределения
отдельных случайных величин, входящих
в систему, характеризуют каждую из
случайных величин в отдельности, но
ничего не говорят о том, как они связаны
между собой. С другой стороны, искомый
закон распределения системы должен
содержать все сведения о случайных
величинах системы, в том числе и о
характере связей между ними.
Таким образом,
если случайные величины
зависимы между собой, то закон распределения
системы не может быть выражен через
законы распределения отдельных случайных
величин, входящих в систему. Это приводит
к необходимости введения условных
законов распределения.
Распределение
одной случайной величины, входящей в
систему, найденное при условии, что
другая случайная величина, входящая в
систему, приняла определенное значение,
называется условным законом распределения.
Условный закон
распределения можно задавать как
функцией распределения, так и плотностью
распределения. Условная функция
распределения обозначается
,
условная плотность распределения(мы записали условные законы распределения
случайной величиныпри условии, что другая случайная
величинаприняла определенное значение).
Плотностью
распределения для случайной величины
при условии, что случайная величина
приняла определенное значение (условной
плотностью распределения)
назовем величину
.
Аналогично,
плотностью распределения для случайной
величины
при условии, что случайная величина
приняла определенное значение, назовем
величину
.
Осюда получаем,
что
,
или, с учетом формул
(5.3),
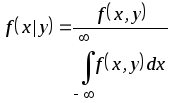
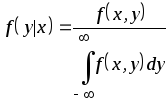
Условная плотность
распределения обладает всеми свойствами
безусловной плотности распределения.
В частности,
,
6.Числовые
характеристики условных законов
распределения.
Для описания
условных законов распределения мы можем
использовать различные характеристики,
подобно тому как мы имели для одномерных
распределений.
Наиболее важной
характеристикой является условное
математическое ожидание.
Условным
математическим ожиданием дискретной
случайной величины
при
(
– определенное возможное значение
случайной величины)
называется сумма произведений возможных
значенийна их условные вероятности:
.
Для непрерывных
случайных величин
,
где
– условная плотность распределения
случайной величиныпри
.
Аналогично,
условным математическим ожиданием
дискретной случайной величины
при
называется сумма произведений возможных
значенийна их условные вероятности:
.
Для непрерывных
случайных величин
,
где
– условная плотность распределения
случайной величиныпри
.
Подобным образом
вводятся условные дисперсии и условные
моменты более высоких порядков.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Двумерная непрерывная случайная величина
- Краткая теория
- Примеры решения задач
Краткая теория
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Непрерывной называют двумерную величину, составляющие которой непрерывны.
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Функция распределения двумерной случайной величины и ее свойства
Функцией распределения двумерной случайной величины
называют функцию
, определяющую для каждой
пары чисел
вероятность того, что
примет значение, меньшее
, и при этом
примет значение, меньшее
.
Свойство 1.
Значения
функции распределения удовлетворяют двойному неравенству:
Свойство 2.
есть неубывающая функция по каждому аргументу,
то есть:
если
если
Свойство 3.
Имеют место предельные соотношения:
1)
2)
3)
4)
Свойство 4.
При
функция распределения системы становится
функцией распределения составляющей
:
При
функция распределения системы становится
функцией распределения составляющей
:
Плотность распределения двумерной случайной величины и ее свойства
Плотностью совместного распределения вероятностей
двумерной непрерывной случайной величины
называют вторую смешанную частную производную
от функции распределения:
Зная
плотность совместного распределения
можно найти функцию распределения
по формуле:
Свойство 1.
Двумерная
плотность вероятности неотрицательна:
Свойство 2.
Двойной
несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Безусловные и условные законы распределения составляющих
Пусть
известна плотность совместного распределения вероятностей системы двух
случайных величин. Найдем плотности распределения каждой из составляющих.
Аналогично
находится плотность распределения составляющей
:
Итак,
плотность распределения одной из составляющих равна несобственному интегралу с
бесконечными пределами от плотности совместного распределения системы, причем
переменная интегрирования соответствует другой составляющей.
Пусть
– непрерывная двумерная случайная величина.
Условной
вероятностью
распределения составляющих
при данном значении
называют отношение плотности совместного
распределения
системы
к плотности распределения
составляющей
:
Аналогично
определяется условная плотность составляющей
при данном значении
:
Если
известна плотность совместного распределения
, то условные плотности
составляющих могут быть найдены по формулам:
Эти
формулы можно записать в виде:
Аналогично
определяется условная плотность составляющей
при данном значении
:
То есть
умножая закон распределения одной из составляющих на условный закон
распределения другой составляющей, найдем закон распределения системы случайных
величин.
Смежные темы решебника:
- Двумерная дискретная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Примеры решения задач
Пример 1
Найти
плотность совместного распределения f(x,y) системы случайных величин (X,Y) по
известной функции распределения:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
По определению плотности совместно
распределения:
Искомая плотность совместного распределения:
Пример 2
Найти
функцию распределения системы случайных величин F(x,y) по известной плотности
совместного распределения f(x,y):
Решение
Воспользуемся
формулой:
В нашем
случае:
Ответ:
Пример 3
Двумерная
случайная величина (X,Y) имеет равномерное распределение вероятностей в
треугольнике ABC. Определить функции плотности распределения
компонент этой случайной величины f(x), f(y), их математические
ожидания M(X), M(Y), дисперсии D(X), D(Y),
коэффициент корреляции rxy. Выяснить, являются ли
случайные величины X и Y независимыми?
A(0;0),B(-1;1),C(1;1)
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
где
– площадь треугольника
Разделим
область
на две равные части вдоль оси
, тогда из условия:
или
Тогда
плотность двумерной случайной величины
:
Вычислим
плотность составляющей
:
при
:
Откуда
плотность составляющей
:
Вычислим
плотность составляющей
:
при
Плотность
составляющей
:
Найдем
условную плотность составляющей
:
при
Следовательно,
случайные величины
и
зависимы
Найдем
математическое ожидание случайной величины
:
Найдем
дисперсию случайной величины
:
Найдем
математическое ожидание случайной величины
:
Найдем
дисперсию случайной величины
:
Найдем
математическое ожидание двумерной случайной величины
:
Тогда
ковариация:
Значит
коэффициент корреляции:
Следовательно,
случайные величины
и
– зависимые, но некоррелированные
Пример 4
Двумерная
случайная величина (X,Y) имеет плотность
распределения:
Найти
вероятность попадания значения (X,Y) в область x1≤x≤x2,
y1≤y≤y2, вероятность попадания значения X в
интервал x1≤x≤x2, математическое ожидание M[X] и
условное математическое ожидание M[Y⁄X=x].
a=8, b=2, x1=6, x2=9, y1=0, y2=4
Решение
Найдем
вероятность попадания в область
по формуле:
При
вычислении интеграла учитывается та часть области
, где
, т.е.
Плотность
вероятности для составляющей
имеет вид:
Если
или
, то
и
. При
находим:
Таким
образом, плотность имеет вид:
Тогда:
Условное математическое ожидание
определяется с
помощью условной плотности распределения
составляющей
Получаем:
Искомое
математическое ожидание:
- Краткая теория
- Примеры решения задач
Двумерная непрерывная случайная величина
Ранее мы разобрали примеры решений задач для одномерной непрерывной случайной величины. Перейдем к более сложному случаю – двумерной непрерывной случайной величине $(X,Y)$ (или двумерному вектору). Кратко выпишем основы теории.
Понравилось? Добавьте в закладки
Система непрерывных случайных величин: теория
Двумерная непрерывная СВ задается своей функцией распределения $F(x,y)=P(Xlt x, Ylt y)$, свойства которой аналогичны свойствам одномерной ФР. Эта функция должна быть непрерывна, дифференцируема и иметь вторую смешанную производную, которая будет как раз плотностью распределения вероятностей системы непрерывных случайных величин:
$$
f(x,y)= frac{partial ^2}{partial x partial y} F(x,y)
$$
Зная плотность совместного распределения, можно найти одномерные плотности для $X$ и $Y$:
$$
f(x)= int_{-infty}^{infty} f(x,y) dy, quad f(y)= int_{-infty}^{infty} f(x,y) dx.
$$
Вероятность попадания случайного вектора в прямоугольную область можно вычислить как двойной интеграл от плотности (по этой области) или через функцию распределения:
$$P(x_1 le X le x_2, y_1 le Y le y_2) = F(x_2, y_2)-F(x_1, y_2)-F(x_2, y_1)+F(x_1, y_1).$$
Как и для случая дискретных двумерных СВ вводится понятие условного закона распределения, плотности которых можно найти так:
$$
f(x|y)=f_y(x)= frac{f(x,y)}{f(y)}, quad f(y|x)=f_x(y)= frac{f(x,y)}{f(x)} $$
Если для всех значений $(x,y)$ выполняется равенство
$$f(x,y) =f(x)cdot f(y),$$
то случайные величины $X, Y$ называются независимыми (их условные плотности распределения совпадают с безусловными). Для независимых случайных величин выполняется аналогичное равенство для функций распределений:
$$F(x,y) =F(x)cdot F(y).$$
Для случайных величин $X,Y$, входящих в состав случайного вектора, можно вычислить ковариацию и коэффициент корреляции по формулам:
$$
cov (X,Y)=M(XY)-M(X)M(Y)= int_{-infty}^{infty}int_{-infty}^{infty} (x-M(X))(y-M(Y)) f(x,y) dxdy, \
r_{XY} = frac{cov(X,Y)}{sqrt{D(X)D(Y)}}.
$$
В этом разделе мы приведем примеры задач с полным решением, где используются непрерывные двумерные случайные величины (системы случайных величин).
Примеры решений
Задача 1. Дана плотность распределения вероятностей системы
$$
f(x)=
left{
begin{array}{l}
C, mbox{ в треугольнике} O(0,0), A(4,0), B(4,1)\
0, mbox{ в остальных точках} \
end{array}
right.
$$
Найти:
$C, rho_1(x), rho_2(y), m_x, m_y, D_x, D_y, cov(X,Y), r_{xy}, F(2,10), M[X|Y=1/2]$.
Задача 2. Дана плотность распределения $f(x,y)$ системы $X,Y$ двух непрерывных случайных величин в треугольнике АВС.
1.1. Найдите константу с.
1.2. Найдите $f_X(x), f_Y(y)$ – плотности распределения с.в. Х и с.в. Y.
Выясните, зависимы или нет с.в. Х и Y. Сформулируйте критерий независимости системы непрерывных случайных величин.
1.3. Найдите математическое ожидание и дисперсию с.в. Х и с.в. Y. Поясните смысл найденных характеристик.
1.4. Найдите коэффициент корреляции с.в. Х и Y. Являются ли случайные величины коррелированными? Сформулируйте свойства коэффициента корреляции.
1.5. Запишите уравнение регрессии с.в. Y на Х и постройте линию регрессии в треугольнике АВС.
1.6. Запишите уравнение линейной среднеквадратичной регрессии с.в. Y на Х и постройте эту прямую в треугольнике АВС. $$ f(x,y)=csqrt{xy}, quad A(0;0), B(-1;-1), C(-1;0) $$
Задача 3. Интегральная функция распределения случайного вектора (X,Y):
$$
F(x)=
left{
begin{array}{l}
0, mbox{ при } x le 0 mbox{ или } yle 0\
(1-e^{-2x})(1-e^{-3y}), mbox{ при } x gt 0 mbox{ и } ygt 0\
end{array}
right.
$$
Найти центр рассеивания случайного вектора.
Задача 4. Плотность совместного распределения непрерывной двумерной случайной величины (Х, У)
$$f(x,y)=C e^{-x^2-2xy-4y^2}$$
Найти:
а) постоянный множитель С;
б) плотности распределения составляющих;
в) условные плотности распределения составляющих.
Задача 5. Задана двумерная плотность вероятности системы двух случайных величин: $f(x,y)=1/2 sin(x+y)$ в квадрате $0 le x le pi/2$, $0 le y le pi/2$, вне квадрата $f(x,y)=0$. Найти функцию распределения системы (X,Y).
Задача 6. Определить плотность вероятности, математические ожидания и корреляционную матрицу системы случайных величин $(X,Y)$, заданных в интервалах $0 le x le pi/2$, $0 le y le pi/2$, если функция распределения системы $F(x,y)=sin x sin y$.
Задача 7. Плотность вероятности системы случайных величин равна
$$f(x,y) = c(R-sqrt{x^2+y^2}), quad x^2+y^2 lt R^2.$$
Определить:
А) постоянную $c$;
Б) вероятность попадания в круг радиуса $alt R$, если центры обоих кругов совпадают с началом координат.
Задача 8. Совместная плотность вероятности системы двух случайных величин X и Y
$$f(x,y)=frac{c}{36+9x^2+4y^2+x^2y^2}.$$
Найти величину $с$; определить законы распределения $F_1(x)$, $F_2(y)$, $f_1(x)$, $f_2(y)$, $f(x/y)$; построить графики $F_1(x)$, $F_2(y)$; вычислить моменты $m_x$, $m_y$, $D_x$, $D_y$, $K_{xy}$.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по теории вероятности онлайн
Больше 11000 решенных и оформленных задач по теории вероятности:
Содержание:
Системы случайных величин или случайные векторы:
При изучении случайных явлений в зависимости от их сложности приходится использовать два, три и большее число случайных величин.
Например, 1) попадание снаряда в цель определяется не одной, а двумя случайными величинами: абсциссой и ординатой точки попадания, 2) случайное отклонение точки разрыва снаряда при дистанционной стрельбе определяется комплексом трех случайных величин: тремя координатами этой точки.
Определение 57. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин или к случайному вектору.
(X, Y) – двумерный случайный вектор или система двух СВ.
Изучать систему – значит изучать сами случайные величины, ее составляющие; связи и зависимости между ними.
Геометрическая интерпретация системы: 1) систему двух случайных величин (X, У) рассматривают как случайную точку на плоскости (Охх) или как случайный вектор с составляющими X, У; 2) систему трех случайных величин (X, У, Z) рассматривают как случайную точку на плоскости (Оxyz) или как случайный вектор с составляющими X, У; Z и т.д.
В зависимости от типа случайных величин, образующих систему, могут быть дискретные, непрерывные и смешанные системы.
Определение 58. Двумерный случайный вектор (X, У) называется вектором дискретного типа (СВДТ), если множество его возможных значений не более, чем счетно.
Определение 59. (первое определение) Двумерный случайный вектор (X, У) называется вектором непрерывного типа (СВНТ), если множество его возможных значений непрерывно заполняет некоторую область плоскости (Оху)-
Определение 60. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Законы распределения СВДТ и СВНТ
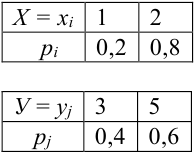
Таблица распределения – закон распределения СВДТ:
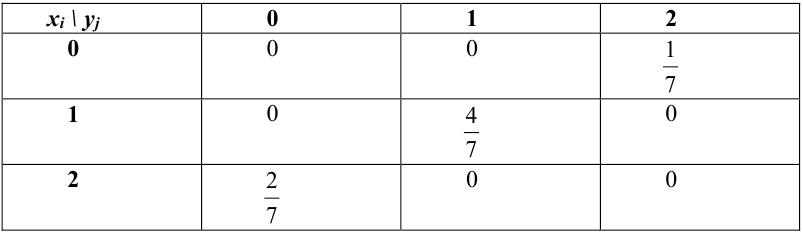
Рассмотрим двумерный случайный вектор (X, У), где X и У – дискретные случайные величины с возможными значениями
Пример:
Из цифр 1, 2, 3, 4, 6, 8, 9 наудачу отбирают две цифры. Х – число четных цифр в выборке, Y – число нечетных. Описать закон распределения.
Решение.
X (четные) – 2, 4, 6, 8; Y ( нечетные) – 1, 3, 9. Следовательно, возможные значения X 
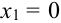
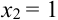
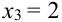
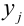
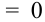
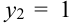
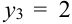
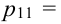
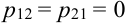
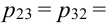
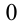
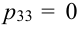
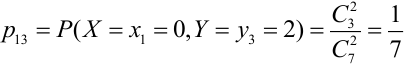
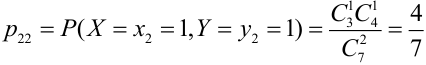
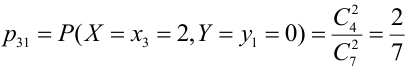
Таблица распределения имеет вид:
Проверка:
Пример:
Дана таблица распределения случайного вектора (X, Y). Получить ряды распределения для Х и Y отдельно.
Решение.
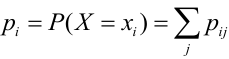
Проверка:
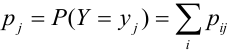
Проверка:
Функция распределения – закон распределения СВДТ и СВНТ
Функция распределения – универсальный закон распределения случайных векторов как дискретного, так и непрерывного типа.
Определение 61. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств: X < х, Y < у, т.е.
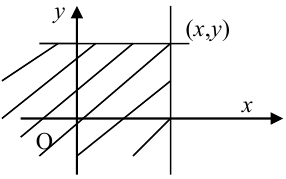
Геометрически F(x,y) представляет вероятность попадания случайной точки (X,Y) в левый нижний бесконечный квадрант плоскости с вершиной в точке (х,у).
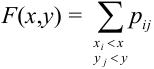
Свойства F(x;y).
1. Условие согласованности:
Пояснение. Отодвигая одну из границ квадранта в бесконечность, получаем полуплоскость, вероятность попадания в которую есть функция распределения одной случайной величины.
2.
Пояснение. Квадрант обращается во всю координатную плоскость, попадание случайной точки в которую есть достоверное событие.
3.
Пояснение. Отодвигая ту или иную границу квадранта в (
4. F(x, у) – неубывающая функция по каждому аргументу.
5. Вероятность попадания случайной точки (X, У) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
Определение 62. (второе определение) Двумерный случайный вектор называется случайным вектором непрерывного типа (СВНТ), если его функция распределения непрерывна на всей плоскости и существует неотрицательная и интегрируемая по Риману в бесконечных пределах по х, у функция 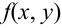
Пример №1
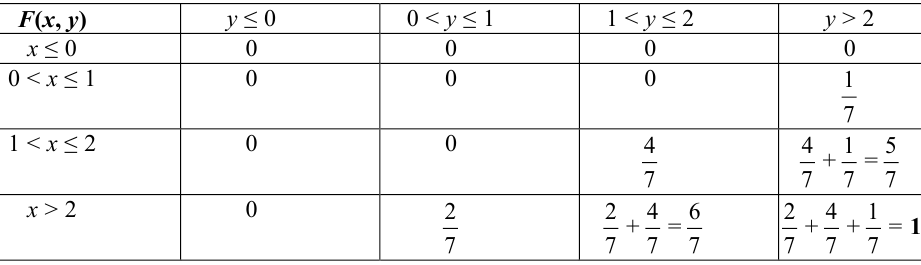
Найти функцию распределения, если случайный вектор задан таблицей распределения:
Решение.
Случайный вектор дискретного типа, следовательно,
Плотность распределения (Для СВНТ)
Определение 63. (первое определение) Плотностью распределения системы двух непрерывных случайных величин называется предел отношения вероятности попадания случайной точки (X, Y) в элементарный прямоугольник к площади прямоугольника, когда оба его размера стремятся к нулю:
Распишем интервальную вероятность с помощью функции распределения:
Правая часть равенства – определение смешанной производной функции двух переменных F(x, у), отсюда следует
Определение 64. (второе определение) Плотностью распределения системы двух непрерывных случайных величин называется смешанная частная производная от функции распределения системы:
Отсюда,
Геометрически 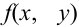
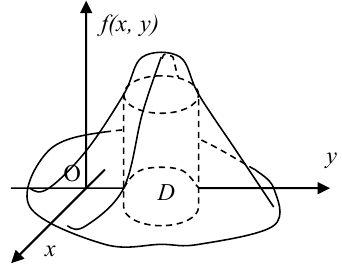
Вероятность попадания случайной точки в некоторую область D плоскости (Oxy) находится по формуле:
Геометрически вероятность попадания случайной точки в область D плоскости (Oxy) изображается объемом цилиндрического тела, ограниченного поверхностью распределения и опирающегося на эту область.
Свойства плотности
1. 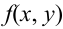
2. Условие нормировки:
Пример №2
Дана плотность распределения непрерывного вектора
Найти: 1) коэффициент а, 2) функцию распределения F(x, у), 3) вероятность попадания случайной точки в прямоугольник с вершинами в точках O(0,0), A(0,1),
Решение.
1) Для вычисления коэффициента а применим условие нормировки:
2) По определению
3) Вероятность попадания в прямоугольник.
1 способ:
2 способ (по 5 свойству):
Пример №3
Дана плотность распределения непрерывного вектора 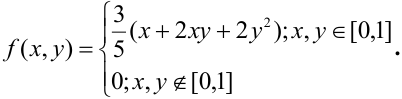
Решение.
Плотность распределения задана в квадрате. Область пересечения квадрата с заданным треугольником заштрихованный треугольник, ограниченный снизу прямой 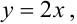
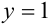
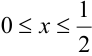
Плотности распределения отдельных величин, входящих в систему
Пусть известна плотность распределения 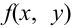
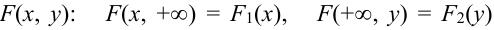
Отсюда, дифференцированием первого равенства по х, а второго по у, получим, что плотности распределения одной из величин равны интегралу от плотности распределения системы в бесконечных пределах по аргументу, соответствующему другой случайной величине:
Ставится вопрос, как по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. В общем случае эта задача не разрешима, но, с другой стороны, закон распределения системы должен содержать все сведения о величинах, входящих в систему, в том числе и сведения о том, как они связаны между собой.
Определение 65. Случайные величины X и Y, входящие в систему, называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае, они называются зависимыми.
Теорема. Для того, чтобы дискретные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
Для того, чтобы непрерывные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
Пример №4
Дана плотность распределения непрерывного вектора:
Зависимы или независимы случайные величины, входящие в систему?
Решение.
Представим плотность в виде произведения:
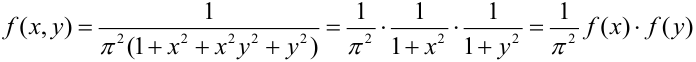
Пример №5
Дано распределение дискретных независимых случайных величин Х и Y:
Записать закон распределения случайного вектора (Х + Y).
Решение.
Найдем возможные значения случайного вектора (Х+ Y): 1 + 3 = 4, 2 + 3 =5, 1+5 = 6, 2 + 5 = 7.
Найдем их вероятности, пользуясь условием независимости:
Следовательно, ряд распределения случайного вектора (Х + Y) имеет вид:
Замечание. Одним из наиболее простых распределений системы двух непрерывных величин является равномерное распределение.
Определение 66. Система двух непрерывных случайных величин имеет равномерное распределение в области D плоскости (Оху), если плотность распределения в точках области D постоянна и равна нулю в остальных точках плоскости:
В силу свойства 2 плотности имеем, что 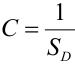
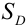
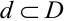
Определение 67. Пусть Х и Y независимые величины, распределенные по нормальному закону, их плотности распределения имеет вид:
Следовательно, плотность распределения системы (Х,Y) на основании теоремы умножения плотностей распределения для случая независимых величин получим в виде
Если X и Y зависимы между собой, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему, что привело к введению условных законов распределения.
Определение 68. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Обозначим G (х,у) – множество возможных значений случайного вектора (X, Y).
Рассмотрим СВДТ.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у называется совокупность возможных значений 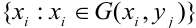
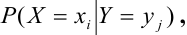
Рассмотрим CBHT.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у :
Теорема (умножения законов распределения):
Условие нормировки:
Условие независимости Х от Y:
Числовые характеристики системы
Определение 69. Начальным моментом 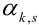
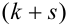
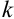
Математическое ожидание дискретных случайных величин Х и Y, входящих в систему:
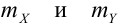
Определение 70. Центральным моментом 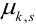
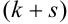
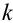
Дисперсия случайных величин X и Y, входящих в систему – характеристика рассеивания случайной точки в направлении осей (ох) и (оу):
Дисперсия дискретных случайных величин Х и Y, входящих в систему:
Дисперсия непрерывных случайных величин Х и Y, входящих в систему:
Замечание. Для краткого описания условных законов распределения используются различные характеристики, наиболее важной из которых является математическое ожидание:
Определение 71. Условным математическим ожиданием дискретной случайной величины X при условии, что Y принимает одно из своих возможных значений 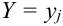
Для непрерывной случайной величины X:
Аналогично, вводится понятие условного мат. ожидания для СВ Y.
Пример №6
По некоторой цели производится два выстрела. Вероятность попадания при одном выстреле равна р. Рассмотрим две случайные величины: X – число попаданий в цель, Y – число промахов. Составить таблицу распределения, записать функцию распределения системы F(x,y) и найти числовые характеристики
Решение.
Случайный вектор дискретного типа, следовательно,
Пояснение:
Ковариация, корреляция и линии регрессии
Особую роль при исследовании системы играет второй смешанный центральный момент.
Определение 72. Второй смешанный центральный момент 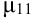
Теория корреляции решает две задачи: 1) установление формы связи между случайными величинами, 2) определение тесноты и силы этой связи.
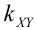
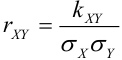
(Иногда его обозначают как 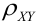
Средние квадратические отклонения случайных величин X и Y равны
Определение 17. X и Y называются некоррелированными случайными величинами, если их коэффициент корреляции 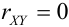
Свойства коэффициента корреляции
Свойства коэффициента корреляции 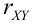
1. Если X и Y – независимые СВ, то 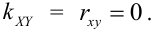
2.
3. В случае 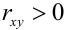
4. В случае 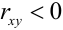
Взаимная связь двух случайных величин, помимо 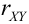
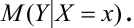
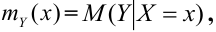
Аналогично, зависимость Х от Y описывает функция
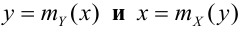
Линии, определенные этими уравнениями, называются кривыми или линиями регрессии. (Вводятся лишь для непрерывных СВ, для ДСВ линии будут состоять из точек.)
Если обе линии регрессии – прямые, то корреляционную зависимость называют линейной (линейная корреляция). Для нормально распределенного случайного вектора (X,Y) уравнения регрессии линейные:
Связь коэффициента корреляции и линий регрессии
1) Если 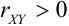
2) Если 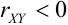
3) Если 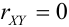
4) Если, 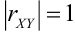
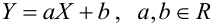
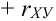
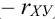
Часто пишут уравнение в виде: 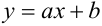
Определение 73. Ковариационной матрицей случайного вектора называется симметрическая действительная матрица, элемент которой представляет собой ковариации соответствующих пар компонент:
Определение 74. Корреляционной матрицей случайного вектора называется нормированная ковариационная матрица
Пример №7
Дано уравнение парной регрессии 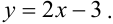
Решение.
Из рассмотрения исключаем 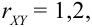
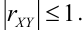
Замечание. Можно было знак 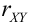
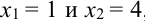
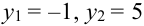
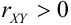
Пример №8
Дано уравнение парной регрессии 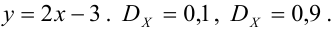
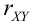
Решение.
Из формулы 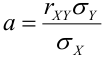
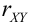
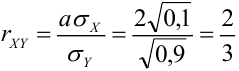
Свойства математического ожидания и дисперсии
1. X, Y как зависимые, так и независимые случайные величины, тогда
2.
Если X, Y – некоррелированные, то
Если X, Y- независимые, то
3.
Если X, Y- некоррелированные, то
4. Если X, Y-независимые, то
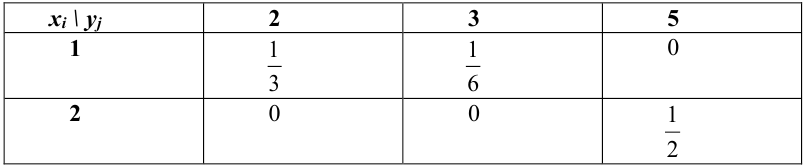
Пример №9
Даны законы распределения случайных величин X, Y:
Найти
Решение.
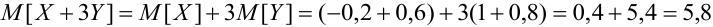
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
- Точечные оценки, свойства оценок
- Алгебра событий – определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события – определение и вычисление
В практических применениях теории вероятностей очень часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами, образующими комплекс или систему. Например, точка попадания снаряда определяется не одной случайной величиной, а двумя: абсциссой и ординатой — и может быть рассмотрена как комплекс двух случайных величин. Аналогично точка разрыва дистанционного снаряда определяется комплексом трех случайных величин. При стрельбе группой из n выстрелов совокупность точек попадания на плоскости может рассматриваться как комплекс или система 2n случайных величин: n абсцисс и n ординат точек попадания. Осколок, образовавшийся при разрыве снаряда, характеризуется рядом случайных величин: весом, размерами, начальной скоростью, направлением полета и т. д. Условимся систему нескольких случайных величин X, Y ,…,W обозначать (X, Y,…, W).
Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, её составляющих: помимо этого, они включают также взаимные связи (зависимости) между случайными величинами.
При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин (X, Y) можно изображать случайной точкой на плоскости с координатами X и Y (рис. 8.1.1), Аналогично система трёх случайных величин может быть изображена случайной точкой в трёхмерном пространстве. Часто бывает удобно говорить о системе n случайных величин как о «случайной точке в пространстве n измерений». Несмотря на то, что последняя интерпретация не обладает непосредственной наглядностью, пользование ею даёт некоторый выигрыш в смысле общности терминологии и упрощения записей.
Часто вместо образа случайной точки для геометрической интерпретации системы случайных величин пользуются образом случайного вектора. Систему двух случайных величин при этом рассматривают как случайный вектор на плоскости хОу, составляющие которого по осям представляют собой случайные величины X, Y (рис. 8.1.2). Система трёх случайных величин изображается случайным вектором в трёхмерном пространстве, система n случайных величин —
случайным вектором в пространстве п измерений. При этом теория систем случайных величин рассматривается как теория случайных векторов.
В данном курсе мы будем в зависимости от удобства изложения пользоваться как одной, так и другой интерпретацией.
Занимаясь системами случайных величин, мы будем рассматривать как полные, исчерпывающие вероятностные характеристики — законы распределения, так и неполные — числовые характеристики.
Изложение начнем с наиболее простого случая системы двух случайных величин.
Функция распределения системы двух случайных величин
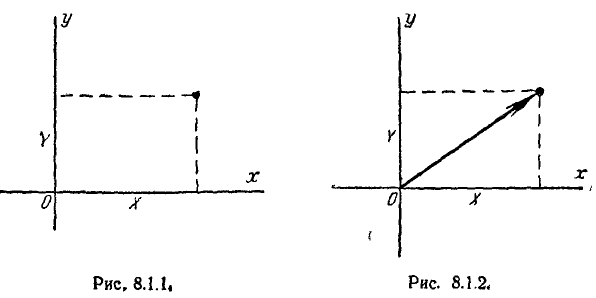
Функцией распределения системы двух случайных величин (X, Y) называется вероятность совместного выполнения двух неравенств Х<х и У<у: 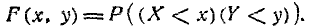
Если пользоваться для геометрической интерпретации системы образом случайной точки, то функция распределения F(x, у) есть не что иное, как вероятность попадании случайной точки (X, Y) в бесконечный квадрант с вершиной в точке (х, у), лежащий левее и ниже ее (рис. 8.2.1). В аналогичной интерпретации функция распределения одной случайной величины X — обозначим её 
В п°5.2 мы привели основные свойства функции распределения F(х) для одной случайной величины. Сформулируем аналогичные свойства для функции распределения системы случайных величин и снова воспользуемся геометрической интерпретацией для наглядной иллюстрации этих свойств.
Функция распределения F(x, у) есть неубывающая функция обоих своих аргументов, т. е.
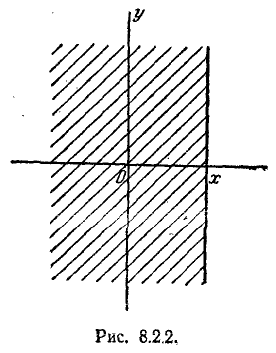
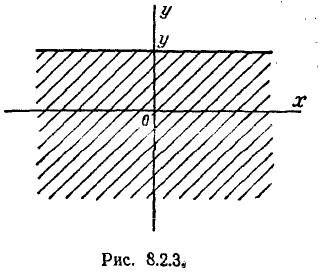
В этом свойстве функции F (х) можно наглядно убедиться, пользуясь геометрической интерпретацией. функции распределения как вероятности попадания в квадрант с вершиной (х, у) (рис. 8.2.1). Действительно, увеличивая х (смещая правую границу квадранта вправо) или увеличивая у (смещая верхнюю границу вверх), мы, очевидно, не можем уменьшить вероятность попадания в этот квадрант.
Повсюду на 
В этом свойстве мы наглядно убеждаемся, неограниченно отодвигая влево правую границу квадранта 

3.При одном из аргументов, равном 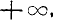
где 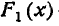
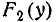
В этом свойстве функции распределения можно наглядно убедиться, смещая ту или иную из границ квадранта на 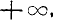
4.Если оба аргумента равны 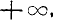
Действительно, при 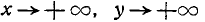
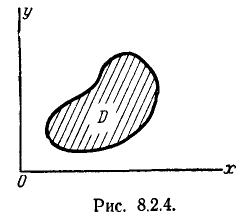
Аналогичным вопросом для системы двух случайных величин является вопрос о вероятности попадания случайной точки (X.Y) в пределы заданной области D на плоскости хОу (рис. 8.2.4).
Условимся событие, состоящее в попадании случайной точки (Х, Y) в область D, обозначать символом
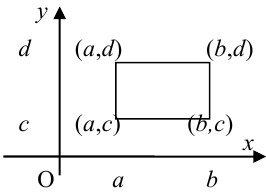
Вероятность попадания случайной точки в заданную область выражается наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.
Вероятность попадания случайной точки в заданную область выражается наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.
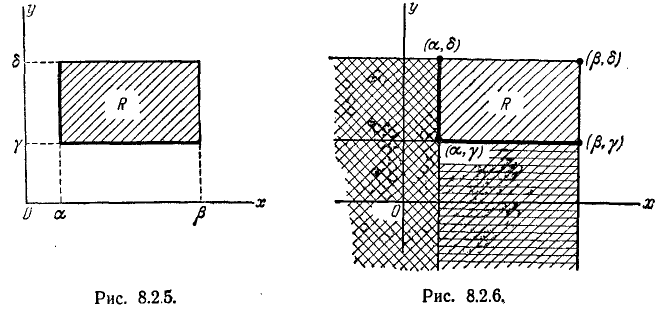
Выразим через функцию распределения системы вероятность по- попадания случайной точки (X, Y) в прямоугольник R, ограничен- ограниченный абсциссами а и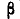
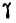
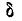
При этом следует условиться, куда мы будем относить границы прямоугольника. Аналогично тому, как мы делали для одной случайной величины, условимся включать в прямоугольник R его нижнюю и левую границы и не включать верхнюю и правую 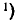
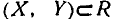
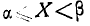
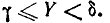
функцию распределения системы. Для этого рассмотрим на плоскости хОу четыре бесконечных квадранта с вершинами в точках 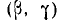
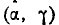
Очевидно, вероятность попадания в прямоугольник R равна вероятности попадания в квадрант 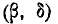
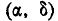
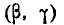
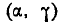
В дальнейшем, когда будет введено понятие плотности распределения системы, мы выведем формулу для вероятности попадания случайной точки в область произвольной формы.
Плотность распределения системы двух случайных величин
Введенная в предыдущем п° характеристика системы — функция распределения — существует для систем любых случайных величин, как прерывных, так я непрерывных. Основное практическое значение имеют системы непрерывных случайных величин. Распределение системы непрерывных величин обычно характеризуют не функцией распределения, а плотностью распределения.
Вводя в рассмотрение плотность распределения для одной случайной величины, мы определяли её как предел отношения вероятности попадания на малый участок к длине этого участка при её неограниченном уменьшении. Аналогично определим плотность распределения системы двух величин.
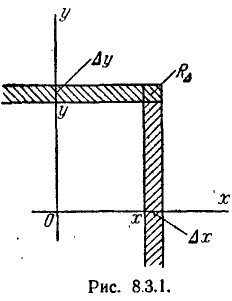
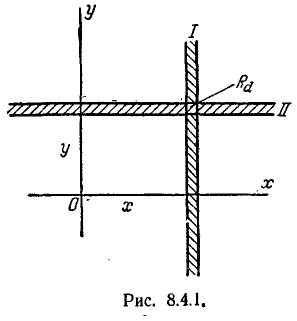
Пусть имеется система двух непрерывных случайных величин (X, Y), которая интерпретируется случайной точкой на плоскости хОу. Рассмотрим на этой плоскости малый прямоугольник 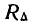
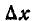
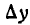
Разделим вероятность попадания в прямоугольник 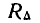
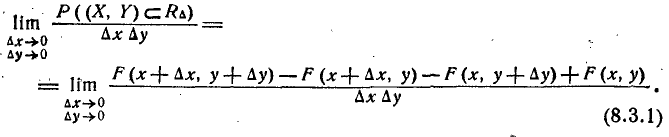
Предположим, что функция F(x, у) не только непрерывна, но и дифференцируема; тогда правая часть формулы (8.3.1) представляет собой вторую смешанную частную производную функции F (х, у) по х и у. Обозначим эту производную f(.г. у):
Функция f (х, у) называется плотностью распределения системы.
Таким образом, плотность распределения системы представляет собой предел отношения вероятности попадания в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю; она может быть выражена как вторая смешанная частная производная функции распределения системы по обоим аргументам.
Если воспользоваться «механической» интерпретацией распределения системы как распределения единичной массы по плоскости хОу, функция f(x, у) представляет собой плотность распределения массы в точке (х, у).
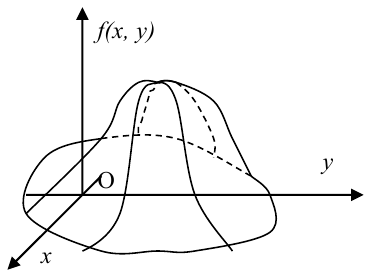
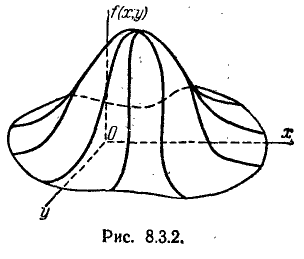
Геометрически функцию f(x, у) можно изобразить некоторой поверхностью (рис. 8.3.2). Эта поверхность аналогична кривой рас- распределения для одной случайной величины и называется поверхностью распределения.
Если пересечь поверхность распределения f(x, у) плоскостью, параллельной плоскости хОу, и спроектировать полученное сечение на плоскость хОу, получится кривая, в каждой точке которой плотность распределения постоянна. Такие кривые называются кривыми равной плотности. Кривые равной плотности, очевидно, представляют собой горизонтали поверхности распределения Часто бывает удобно задавать распределение семейством кривых равной плотности.
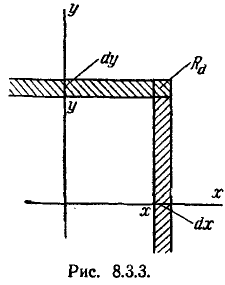
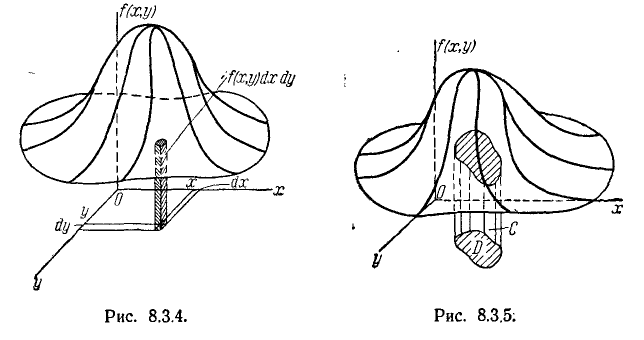
Рассматривая плотность распределения f (х) для одной случайной величины, мы ввели понятие «элемента вероятности» f(x)dx. Это есть вероятность попадания случайной величины X на элементарный участок dx, прилежащий к точке х. Аналогичное понятие «элемента вероятности» вводится и для системы двух случайных величин. Элементом вероятности в данном случае называется выражение
f(x, y)dx dy.
Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами dx,dy примыкающий к точке (х, у) (рис. 8.3.3). Эта вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью f(x, у) и опирающегося на элементарный прямоугольник dx dy (рис. 8.3.4).
Пользуясь понятием элемента вероятности, выведем выражение для вероятности попадания случайной точки в произвольную область D. Эта вероятность, очевидно, может быть получена суммированием (интегрированием) элементов вероятности по всей области D:
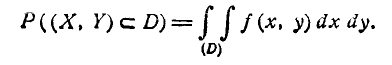
Геометрически вероятность попадания в область D изображается объемом цилиндрического тела С, ограниченного сверху поверхностью распределения и опирающегося на область D (рис. 8.3.5).
Из общей формулы (8.3.3) вытекает формула для вероятности попадания в прямоугольник R, ограниченный абсциссами а и 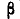
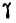
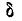
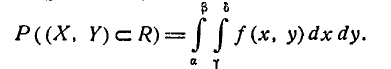
Воспользуемся формулой (8.3.4) для того, чтобы выразить функцию распределения системы F(x, у) через плотность распределения f(x, у). Функция распределения F(x, у) есть вероятность попадания в бесконечный квадрант; последний можно рассматривать как прямоугольник, ограниченный абсциссами 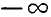
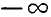
Легко убедиться в следующих свойствах плотности распределения системы:
1.Плотность распределения системы есть функция неотрицательная:
Это ясно из того, что плотность распределения есть предел отношения двух неотрицательных величин: вероятности попадания в прямоугольник и площади прямоугольника — и, следовательно, отрицательной быть не может.
2.Двойной интеграл в бесконечных пределах от плотности распределения системы равен единице:
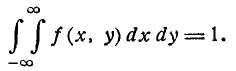
Это видно из того, что интеграл (8.3.6) есть не что иное, как вероятность попадания во всю плоскость хОу, т. е. вероятность достоверного события.
Геометрически это свойство означает, что полный объем тела, ограниченного поверхностью распределения и плоскостью хОу, равен единице.
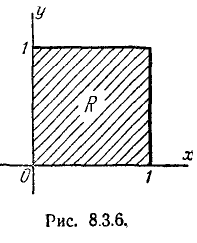
Пример:
Система двух случайных величин (X, У) подчинена закону распределения с плотностью
Найти функцию распределения F (х, у). Определить вероятность попадания случайной точки (X, У) в квадрат R (рис. 8.3.6).
Решение:
Функцию распределения F (х, у) находим по формуле (8.3.5).
Вероятность попадания в прямоугольник R находим по формуле (8.3.4):
Пример:
Поверхность распределения системы (X, У) представляет собой прямой круговой конус, основанием которого служит круг радиуса R
с центром в начале координат. Написать выражение плотности распределения. Определить вероятность того, что случайная точка (х, у) попадет в круг К радиуса а (рис. 8.3.7), причем а < R.
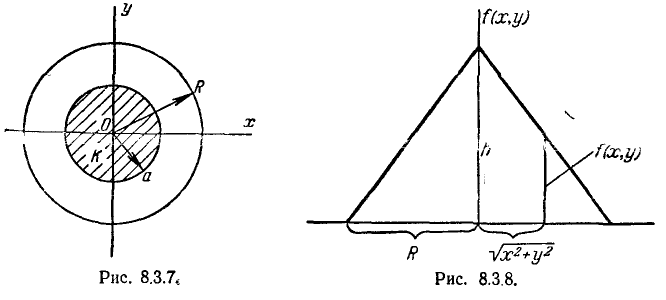
Решение:
Выражение плотности распределения внутри круга К находим из рис. 8.3.8:
где h — высота конуса. Величину h определяем так, чтобы объем конуса был равен единице:
откуда
Вероятность попадания в круг К определяем по формуле (8.3.4): 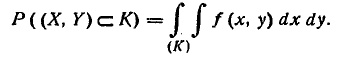
Для вычисления интеграла (8.3.7) удобно перейти к полярной системе координат 
Законы распределения отдельных величии, входящих в систему. Условные законы распределения
Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных величин, входящих в систему. В п° 8.2 мы уже вывели выражения для функций распределения отдельных величин, входящих в систему, через функцию распределения системы, а именно, мы показали, что 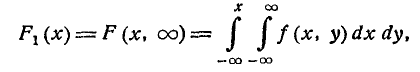
Выразим теперь плотность распределения каждой из величин, входящих в систему, через плотность распределения системы. Пользуясь формулой (8.3.5), выражающей функцию распределения через плотность распределения, напишем:
откуда, дифференцируя по х, получим выражение для плотности распределения величины X:
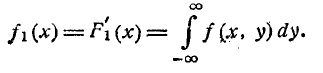
Аналогично
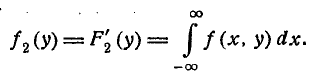
Таким образом, для того чтобы получить плотность распределения одной из величин, входящих в систему, нужно плотность распределения системы проинтегрировать в бесконечных пределах по аргументу, соответствующему другой случайной величине.
Формулы (8.4.1), (8.4.2) и (8.4.3) дают возможность, зная закон распределения системы (заданный в виде функции распределения или плотности распределения), найти законы распределения отдельных величин, входящих в систему. Естественно, возникает вопрос об обратной задаче: нельзя ли по законам распределения отдельных величин, входящих в систему, восстановить закон распределения системы? Оказывается, что в общем случае этого сделать нельзя: зная только законы распределения отдельных величин, входящих в систему, не всегда можно найти закон распределения системы. Дли того чтобы исчерпывающим образом охарактеризовать систему, недостаточно знать распределение каждой из величин, входящих в систему; нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость может быть охарактеризована с помощью так на- называемых условных законов распределения.
Условным законом распределения величины X, входящей в систему (X, Y), называется ее закон распределения, вычисленный при условии, что другая случайная величина Y приняла определенное значение у.
Условный закон распределения можно задавать как функцией распределения, так и плотностью. Условная функция распределения обозначается 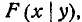
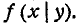
Чтобы нагляднее пояснить понятие условного закона распределения, рассмотрим пример. Система случайных величин L и Q представляет собой длину и вес осколка снаряда. Пусть нас интересует длина осколка L безотносительно к его весу; это есть случайная величина, подчиненная закону распределения с плотностью 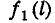
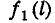
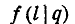
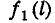
Зная закон распределения одной из величин, входящих в систему, и условный закон распределения второй, можно составить закон распределения системы. Выведем формулу, выражающую это соотношение, для непрерывных случайных величин. Для этого воспользуемся понятием об элементе вероятности. Рассмотрим прилежащий к точке (х, у) элементарный прямоугольник 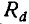
Вероятность произведения этих двух событий, по теореме умножения вероятностей, равна вероятности попадания в элементарную полосу /, умноженной на условную вероятность попадания в элементарную полосу //, вычисленную при условии, что первое событие имело место. Это условие в пределе равносильно условию Х = х; следовательно,
откуда
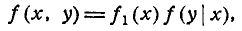
т. е. плотность распределения системы двух величин равна плотности распределения одной из величин, входящих в систему, умноженной на условную плотность распределения другой величины, вычисленную при условии, что первая величина приняла заданное значение.
Формулу (8.4.4) часто называют теоремой умножения законов распределения. Эта теорема в схеме случайных величин аналогична теореме умножения вероятностей в схеме событий.
Очевидно, формуле (8.4.4) можно придать другой вид, если за- задать значение не величины X, а величины Y:
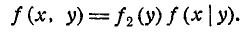
Разрешая формулы (8.4.4) и (8.4.5) относительно f(yx) и f(xy), получим выражения условных законов распределения через безусловные:
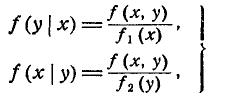
или, применяя формулы (8.4.2) и (8.4.3),
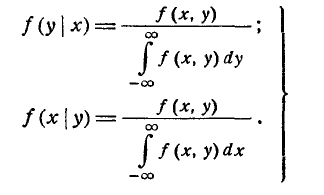
Зависимые и независимые случайные величины
При изучении систем случайных величин всегда следует обращать внимание на степень и характер их зависимости. Эта зависимость может быть более или менее ярко выраженной, более или менее тесной. В некоторых случаях зависимость между случайными величинами может быть настолько тесной, что, зная значение одной случайной величины, можно в точности указать значение другой. В другом крайнем случае зависимость между случайными величинами является настолько слабой и отдаленной, что их можно практически считать независимыми.
Понятие о независимых случайных величинах — одно из важных понятий теории вероятностей.
Случайная величина Y называется независимой от случайной величины X, если закон распределения величины Y не зависит от того, какое значение приняла величина X.
Для непрерывных случайных величин условие независимости К от X может быть записано в виде:
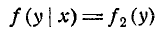
при любом у. Напротив, в случае, если Y зависит от Х, то
Докажем, что зависимость или независимость случайных величин всегда взаимны: если величина Y не зависит от X, то и величина X не зависит от Y.
Действительно, пусть Y не зависит от X:

Из формул (8.4.4) и (8.4.5) имеем:
откуда, принимая во внимание (8.5.1), получим:
что и требовалось доказать.
Так как зависимость и независимость случайных величин всегда взаимны, можно дать новое определение независимых случайных величин.
Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины X и Y называются зависимыми.
Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид: 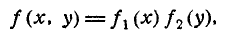
т. е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.
Условие (8.5.2) может рассматриваться как необходимое и достаточное условие независимости случайных величин.
Часто по самому виду функции f(x, у) можно заключить, что случайные величины X, Y являются независимыми, а именно, если плотность распределения f(x, у) распадается на произведение двух функций, из которых одна зависит только от х, другая — только от у, то случайные величины независимы.
Пример. Плотность распределения системы (X, Y) имеет вид:
Определить: зависимы или независимы случайные величины X и Y. Решение. Разлагая знаменатель на множители, имеем:
Из того, что функция f(х, у) распалась на произведение двух функций из которых одна зависит только от х, а другая — только от у, заключаем, что величины X и К должны быть независимы. Действительно, применяя формулы (8.4.2) и (8.4.3), имеем:
аналогично
откуда убеждаемся, что
и, следовательно, величины X и Y независимы.
Вышеизложенный критерий суждения о зависимости или независимости случайных величин исходит из предположения, что закон распределения системы нам известен. На практике чаще бывает наоборот: закон распределения системы (Х, У) не известен; известны только законы распределения отдельных величин, входящих в систему, и имеются основания считать, что величины Х и У независимы. Тогда можно написать плотность распределения системы как произведение плотностей распределения отдельных величин, входящих в систему.
Остановимся несколько подробнее на важных понятиях о «зависимости» и «независимости» случайных величин.
Понятие «зависимости» случайных величин, которым мы пользуемся в теории вероятностей, несколько отличается от обычного понятия «зависимости» величин, которым мы оперируем в математике. Действительно, обычно под «зависимостью» величин подразумевают только один тип зависимости — полную, жесткую, так называемую функциональную зависимость. Две величины X и Y называются функционально зависимыми, если, зная значение одной из них, можно точно указать значение другой.
В теории вероятностей мы встречаемся с другим, более общим, типом зависимости — с вероятностной или «стохастической» зависимостью. Если величина Y связана с величиной X вероятностной зависимостью, то, зная значение X, нельзя указать точно значение Y, а можно указать только ее закон распределения, зависящий от того, какое значение приняла величина X.
Вероятностная зависимость может быть более или менее тесной; по мере увеличения тесноты вероятностной зависимости она все более приближается к функциональной. Таким образом, функциональную зависимость можно рассматривать как крайний, предельный случай наиболее тесной вероятностной зависимости. Другой крайний случай — полная независимость случайных величин. Между этими двумя крайними случаями лежат все градации вероятностной зависимости — от самой сильной до самой слабой. Те физические величины, которые на практике мы считаем функционально зависимыми, в действительности связаны весьма тесной вероятностной зависимостью: при заданном значении одной из этих величин другая колеблется в столь узких пределах, что ее практически можно считать вполне определенной. С другой стороны, те величины, которые мы на практике считаем независимыми, в действительности часто находятся в некоторой взаимной зависимости, но эта зависимость настолько слаба, что ею для практических целей можно пренебречь.
Вероятностная зависимость между случайными величинами очень часто встречается на практике. Если случайные величины X и Y находятся в вероятностной зависимости, это не означает, что с изменением величины X величина Y изменяется вполне определенным образом; это лишь означает, что с изменением величины X величина Y имеет тенденцию также изменяться (например, возрастать или убывать при возрастании X). Эта тенденция соблюдается лишь «в среднем», в общих чертах, и в каждом отдельном случае от нее возможны отступления.
Рассмотрим, например, две такие случайные величины: X — рост наугад взятого человека, Y — его вес. Очевидно, величины X и У находятся в определенной вероятностной зависимости; она выражается в том, что в общем люди с большим ростом имеют больший вес. Можно даже составить эмпирическую формулу, приближенно заменяющую эту вероятностную зависимость функциональной. Такова, например, общеизвестная формула, приближенно выражающая зависимость между ростом и весом:
Y (кг) = Х (см)—100.
Формулы подобного типа, очевидно, не являются точными и выражают лишь некоторую среднюю, массовую закономерность, тенденцию, от которой в каждом отдельном случае возможны отступления.
В вышеприведенном примере мы имели дело со случаем явно выраженной зависимости. Рассмотрим теперь такие две случайные величины: X — рост наугад взятого человека; Z — его возраст. Очевидно, для взрослого человека величины X и Z можно считать практически независимыми; напротив, для ребенка величины X и Z являются зависимыми.
Приведем еще несколько примеров случайных величин, находящихся в различных степенях зависимости.
1.Из камней, составляющих кучу щебня, выбирается наугад один камень. Случайная величина Q — вес камня; случайная величина L — наибольшая длина камня. Величины Q и L находятся в явно выраженной вероятностной зависимости.
2. Производится стрельба ракетой в заданный район океана. Величина 
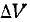
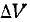
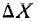
3.Летательный аппарат, находясь в полете, измеряет высоту над поверхностью Земли с помощью барометрического прибора. Рассматриваются две случайные величины: 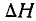
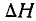
В следующем п° мы познакомимся с некоторыми числовыми характеристиками системы случайных величин, которые дадут нам возможность оценивать степень зависимости этих величин.
Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции
В главе 5 мы ввели в рассмотрение числовые характеристики одной случайной величины X— начальные и центральные моменты различных порядков. Из этих характеристик важнейшими являются две: математическое ожидание 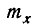
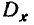
Аналогичные числовые характеристики — начальные и центральные моменты различных порядков — можно ввести и для системы двух случайных величин.
Начальным моментом порядка k, s системы (Х, Y) называется математическое ожидание произведения 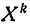
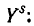
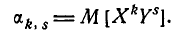
Центральным моментом порядка k, s системы (X, Y) называется математическое ожидание произведения k-й и s-й степени соответствующих центрированных величин: 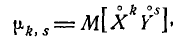
где
Выпишем формулы, служащие для непосредственного подсчета моментов. Для прерывных случайных величин
где 
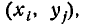
Для непрерывных случайных величин:
где f(x, у) — плотность распределения системы. Помимо чисел k и s, характеризующих порядок момента по от- отношению к отдельным величинам, рассматривается ещё суммарный порядок момента k—s, равный сумме показателей степеней при Х и У. Соответственно суммарному порядку моменты классифицируются на первые, вторые и т. д. На практике обычно применяются только первые и вторые моменты.
Первые начальные моменты представляют собой уже известные нам математические ожидания величин X и У, входящих в систему:
Совокупность математических ожиданий 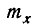
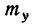
Кроме первых начальных моментов, на практике широко при- применяются ещё вторые центральные моменты системы. Два из них представляют собой уже известные нам дисперсии величин X и У:
характеризующие рассеивание случайной точки в направлении осей Ох и Оу. Особую роль как характеристика системы играет второй смешанный центральный момент:
т. е. математическое ожидание произведения центрированных величин. Ввиду того, что этот момент играет важную роль в теории систем случайных величин, введем для него особое обозначение: 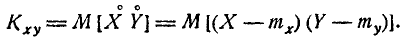
Характеристика 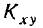
Для прерывных случайных величин корреляционный момент выражается формулой
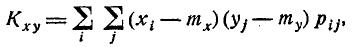
а для непрерывных — формулой
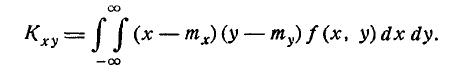
Выясним смысл и назначение этой характеристики. Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеивания величин X и Y, ещё и связь между ними. Для того чтобы убедиться в этом, докажем, что для независимых случайных величин корреляционный момент равен нулю.
Доказательство проведем для непрерывных случайных величин 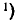
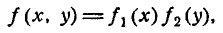
где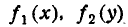
Интеграл
представляет собой не что иное, как первый центральный момент величины X, и, следовательно, равен нулю; по той же причине равен пулю и второй сомножитель; следовательно, для независимых случайных величин 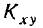
Таким образом, если корреляционный момент двух случайных величин отличен от нуля, это есть признак наличия зависимости между ними.
Из формулы (8.6.7) видно, что корреляционный момент характеризует не только зависимость величин, но и их рассеивание. Действительно, если, например, одна из величин (X, Y) весьма мало отклоняется от своего математического ожидания (почти не случайна),
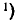
то корреляционный момент будет мал, какой бы тесной зависимостью ни были связаны величины (X,Y ). Поэтому для характеристики связи между величинами (X, Y) в чистом виде переходят от момента 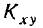
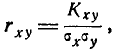
где 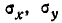
Случайные величины, для которых корреляционный момент (а значит, и коэффициент корреляции) равен нулю, называются некоррелированными (иногда — «несвязанными»).
Выясним, эквивалентно ли понятие некоррелированности случайных величин понятию независимости. Выше мы доказали, что две независимые случайные величины всегда являются некоррелированными. Остаётся выяснить: справедливо ли обратное положение, вытекает ли из некоррелированности величин их независимость? Оказывается — нет. Можно построить примеры таких случайных величин, которые являются некоррелированными, но зависимыми. Равенство нулю коэффициента корреляции — необходимое, но не достаточное условие независимости случайных величин. Из независимости случайных величин вытекает их некоррелированность; напротив, из некоррелированности величин ещё не следует их независимость. Условие независимости случайных величин — более жёсткое, чем условие некоррелированности.
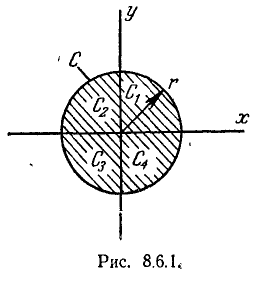
Убедимся с этом на примере. Рассмотрим систему случайных величин (X, Y), распределённую с равномерной плотностью внутри круга С радиуса г с центром в начале координат (рис. 8.6.1).
Плотность распределения величин (X, Y) выражается формулой
Из условия 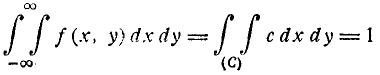
Нетрудно убедиться, что в данном примере величины являются зависимыми. Действительно, непосредственно ясно, что если величина X приняла, например, значение 0, то величина Y может с равной вероятностью принимать все значения от — r до +r; если же величина X приняла значение r, то величина Y может при- принять только одно-единственное значение, в точности равное нулю; вообще, диапазон возможных значений Y зависит от того, какое значение приняла X.
Посмотрим, являются ли эти величины коррелированными. Вычислим корреляционный момент. Имея в виду, что по cображениям симметрии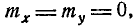
Для вычисления интеграла разобьём область интегрирования (круг С) на четыре сектора 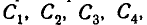
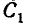
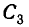
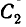
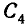
Таким образом, мы видим, что из некоррелированности случайных величин не всегда следует их независимость.
Коэффициент корреляции характеризует не всякую зависимость, а только так называемую линейную зависимость. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или же убывать) по линейному закону. Эта тенденция к линейной зависимости может быть более или менее ярко выраженной, более или менее приближаться к функциональной, т. е. самой тесной линейной зависимости. Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами. Если случайные величины X и У связаны точной линейной функциональной зависимостью:
то 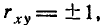
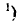
В случае 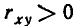

В рассмотренном примере двух случайных величин (X, У), распределённых внутри круга с равномерной плотностью, несмотря на наличие зависимости между X и К, линейная зависимость отсутствует; при возрастании X меняется только диапазон изменения Y,
а его среднее значение не меняется; естественно, величины (X, Y) оказываются некоррелированными.
Приведем несколько примеров случайных величин с положительной и отрицательной корреляцией.
- Вес и рост человека связаны положительной корреляцией.
- Время,. потраченное на регулировку прибора при подготовке его к работе, и время его безотказной работы связаны положительной корреляцией (если, разумеется, время потрачено разумно). Наоборот, время, потраченное на подготовку, и количество неисправностей, обнаруженное при работе прибора, связаны отрицательной корреляцией.
- При стрельбе залпом координаты точек попадания отдельных снарядов- связаны положительной корреляцией (так как имеются общие для всех выстрелов ошибки прицеливания, одинаково отклоняющие от цели каждый из них).
- Производится два выстрела по цели; точка попадания первого выстрела регистрируется, и в прицел вводится поправка, пропорциональная ошибке первого выстрела с обратным знаком. Координаты точек попадания первого и второго выстрелов будут связаны отрицательной корреляцией.
Если в нашем распоряжении имеются результаты ряда опытов над системой двух случайных величин (X, У), то о наличии или отсутствии существенной корреляции между ними легко судить в первом приближении по графику, на котором изображены в виде точек все полученные из опыта пары значений случайных величин. Например, если наблюдённые пары значений величин расположились так, как показано на рис. 8.6.2, то это указывает на ‘наличие явно выраженной положительной корреляции между величинами. Ещё более ярко выраженную положительную корреляцию, близкую к линейной функциональной зависимости, наблюдаем на рис. 8.6.3. На рис. 8.6.4 показан случай сравнительно слабой отрицательной корреляции.
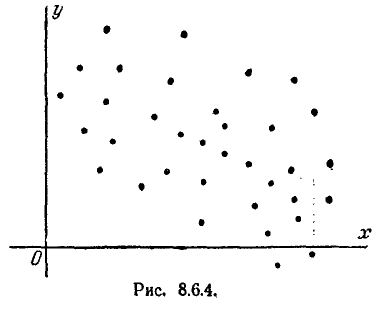
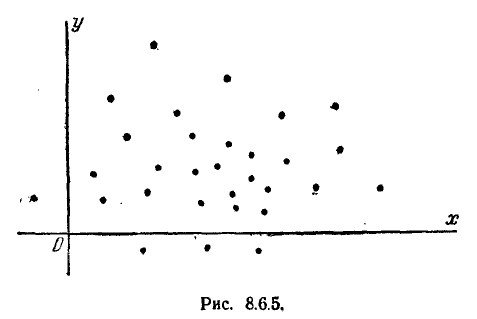
Наконец, на рис. 8.6.5 иллюстрируется случай практически некоррелированных случайных величин. На практике, перед тем как исследовать корреляцию случайных величин, всегда полезно предварительно построить наблюдённые пары значений на графике для первого качественного суждения о типе корреляции.
Способы определения характеристик системы случайных величин из опыта будут освещены в гл. 14.
Система произвольного числа случайных величин
На практике часто приходится рассматривать системы более чем двух случайных величин. Эти системы интерпретируются как случайные точки или случайные векторы в пространстве того или иного числа измерений.
Приведем примеры.
- Точка разрыва дистанционного снаряда в пространстве характеризуется тремя декартовыми координатами (X, У, Z) или тремя сферическими координатами
- Совокупность п последовательных измерений изменяющейся величины X — система п случайных величин
- Производится стрельба очередью из п снарядов. Совокупность координат п точек попадания на плоскости — система 2n случайных величин (абсцисс и ординат точек попадания):
- Начальная скорость осколка — случайный вектор, характеризуемый тремя случайными величинами: величиной скорости
и двумя углами Ф и
, определяющими направление полёта осколка в сферической системе координат.
Полной характеристикой системы произвольного числа случайных величин служит закон распределения системы, который может быть задан функцией распределения или плотностью распределения.
Функцией распределения системы п случайных величин 
Плотностью распределения системы п непрерывных случайных величин называется n-я смешанная частная производная функции 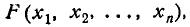
Зная закон распределения системы, можно определить законы распределения отдельных величин, входящих в систему. Функция распределения каждой из величин, входящих в систему, получится, если в функции распределения системы положить все остальные аргументы равными 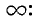
Если выделить из системы величин 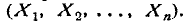
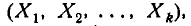
Плотность распределения каждой из величин, входящих в систему, получится, если плотность распределения системы проинтегрировать в бесконечных пределах по всем остальным аргументам:
Плотность распределения частной системы 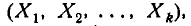
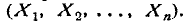
Условным законом распределения частной системы 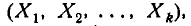


Условная плотность распределения может быть вычислена по формуле
Случайные величины 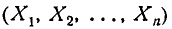
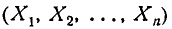
Плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему:
Вероятность попадания случайной точки 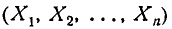
Формула (8.7.9) по существу является основной формулой для вычисления вероятностей событий, не сводящихся к схеме случаев. Действительно, если интересующее нас событие А не сводится к схеме случаев, то его вероятность не может быть вычислена непосредственно. Если при этом нет возможности поставить достаточное число однородных опытов и приближённо определить вероятность события А по его частоте, то типичная схема вычисления вероятности события сводится к следующему. Переходят от схемы событий к схеме случайных величин (чаще всего — непрерывных) и сводят событие А к событию, состоящему в том, что система случайных величин 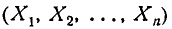
Пример:
Самолёт поражается дистанционным снарядом при условии, если разрыв снаряда произошёл не далее чем на расстоянии R от самолёта (точнее, от условной точки на оси самолёта, принимаемой за его центр). Закон распределения точек разрыва дистанционного снаряда в системе координат, связанной с целью, имеет плотность f (х, у, r). Определить вероятность поражения самолёта.
Решение:
Обозначая поражение самолёта буквой А, имеем:
где интегрирование распространяется по шару С радиуса R с центром в начале координат.
Пример:
Метеорит, встретившийся на пути искусственного спутника Земли, пробивает его оболочку, если: 1) угол в, под которым метеорит встречается с поверхностью спутника, заключён в определённых пределах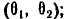
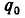
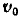
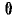
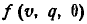
Решение:
Интегрируя плотность распределения 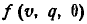
где 

Числовые характеристики системы нескольких случайных величин
Закон распределения системы (заданный функцией распределения или плотностью распределения) является полной, исчерпывающей характеристикой системы нескольких случайных величин. Однако очень часто такая исчерпывающая характеристика не может быть применена. Иногда ограниченность экспериментального материала не даёт возможности построить закон распределения системы. В других случаях исследование вопроса с помощью сравнительно громоздкого аппарата законов распределения не оправдывает себя в связи с невысокими требованиями к точности результата. Наконец, в ряде задач примерный тип закона распределения (нормальный закон) известен заранее и требуется только найти его характеристики.
Во всех таких случаях вместо законов распределения применяют неполное, приближенное описание системы случайных величин с помощью минимального количества числовых характеристик.
Минимальное число характеристик, с помощью которых может быть охарактеризована система n случайных величин 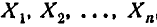
1) п математических ожиданий 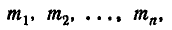
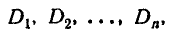
где
характеризующих попарную корреляцию всех величин, входящих в систему.
Заметим, что дисперсия каждой из случайных величин 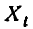
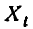
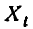
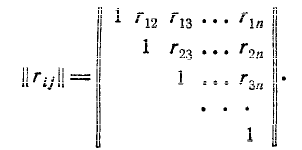
Все корреляционные моменты и дисперсии удобно расположить в виде прямоугольной таблицы (так называемой матрицы):
Эта таблица называется корреляционной матрицей системы случайных величин
Очевидно, что не все члены .корреляционной матрицы различны. Из определения корреляционного момента ясно, что 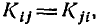
Корреляционную матрицу, составленную из элементов 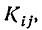
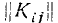
По главной диагонали корреляционной матрицы стоят дисперсии случайных величин 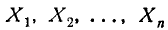
В случае, когда случайные величины 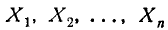
Такая матрица называется диагональной.
В целях наглядности суждения именно о коррелированности случайных величин безотносительно к их рассеиванию часто вместо корреляционной матрицы 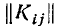
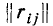
где
Все диагональные элементы этой матрицы, естественно, равны единице. Нормированная корреляционная матрица имеет вид:
Введём понятие о некоррелированных системах случайных величин (иначе — о некоррелированных случайных векторах). Рассмотрим две системы случайных величин:
или два случайных вектора в n-мерном пространстве: 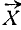
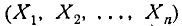
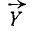
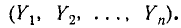
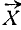
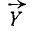
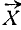
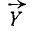
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Нормальный закон распределения для системы случайных величин
- Вероятностное пространство
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность
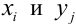

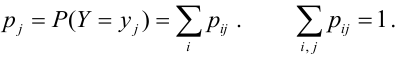
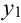

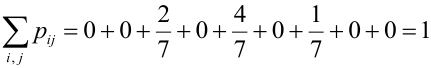
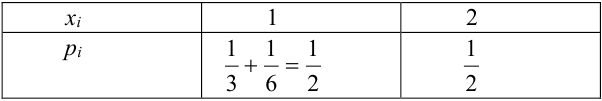
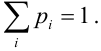

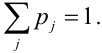
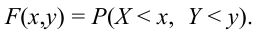
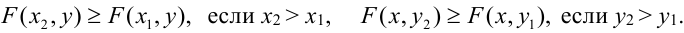
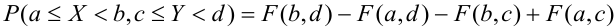
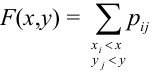
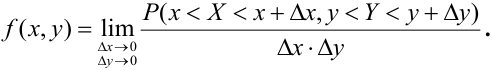
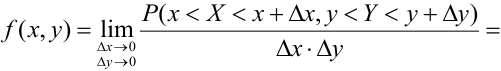
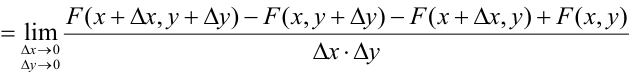
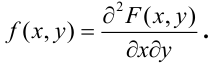
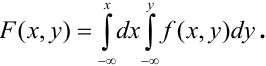
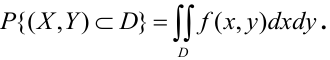
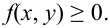
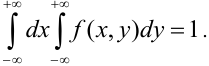
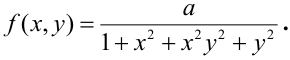
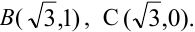
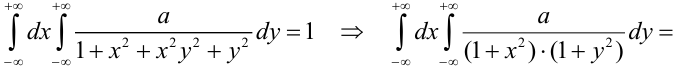
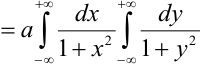
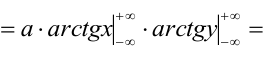
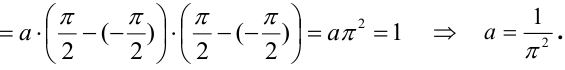
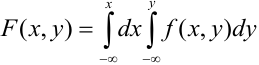
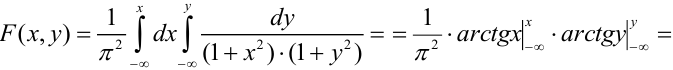
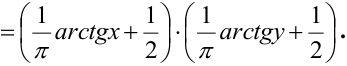
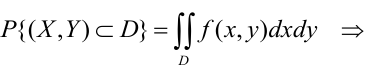
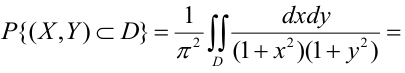
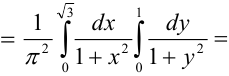
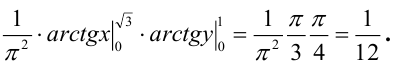
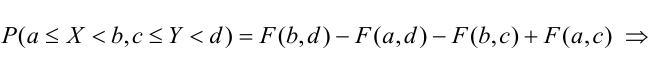
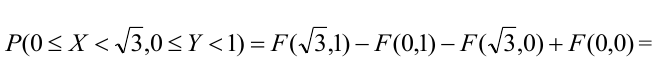
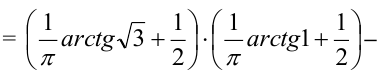
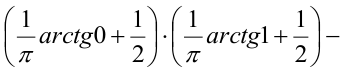
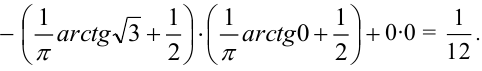
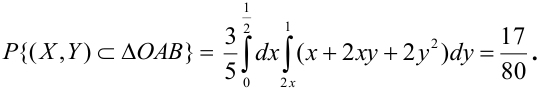
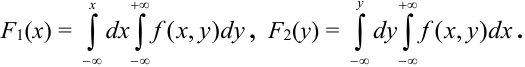
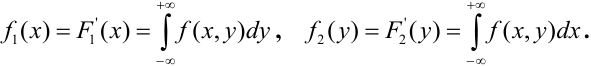
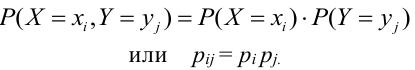
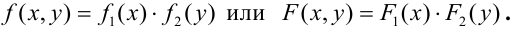
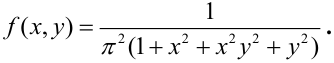
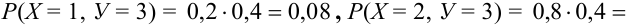
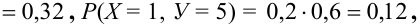
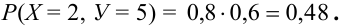

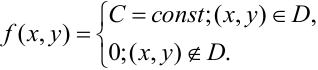
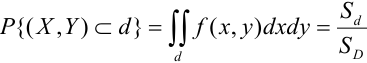
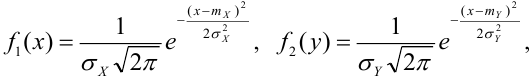
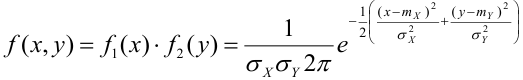
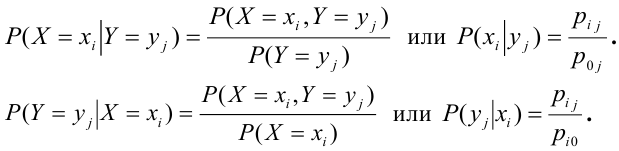
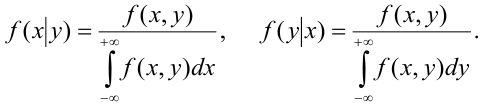
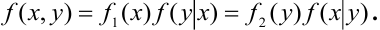
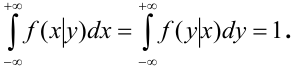
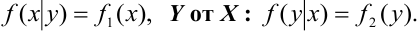
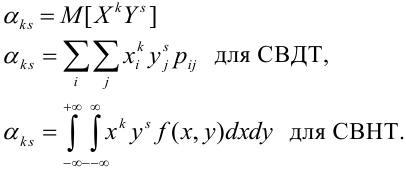
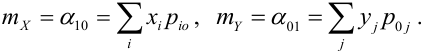
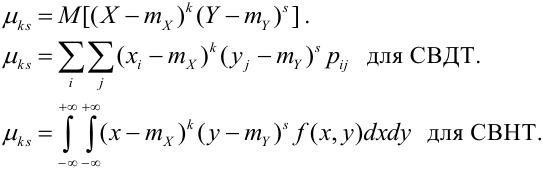

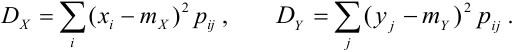
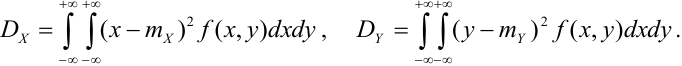
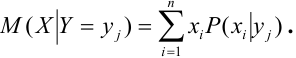
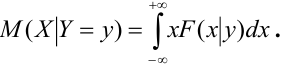
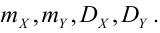

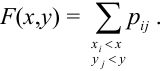


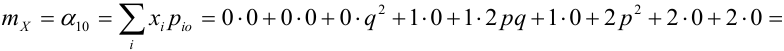
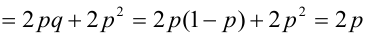
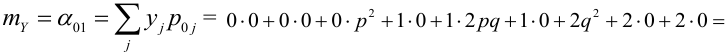
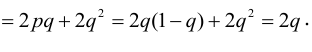
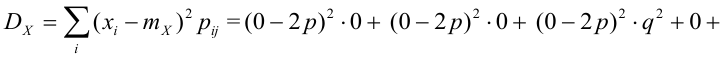
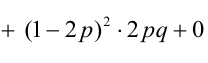
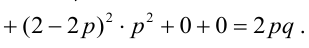
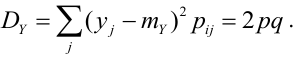
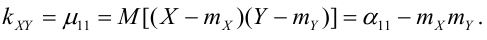
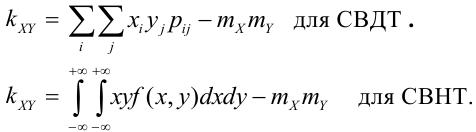
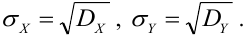
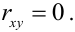
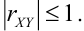
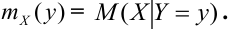
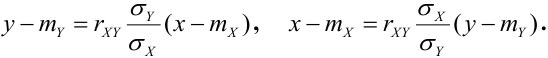
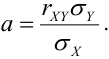
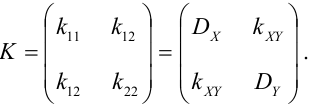
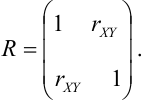
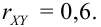
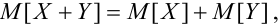
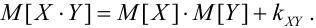
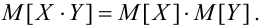
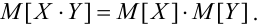
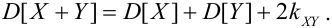
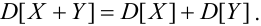
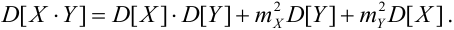
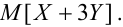

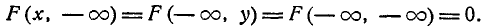
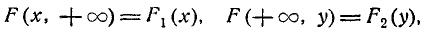
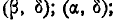
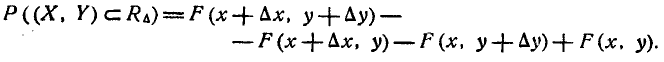
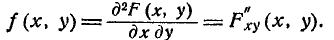
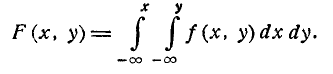
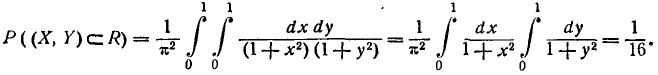
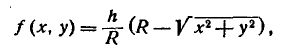
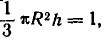
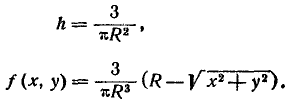
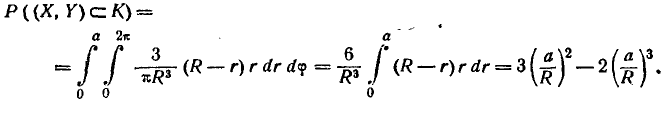
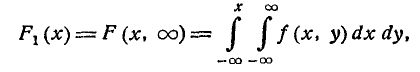
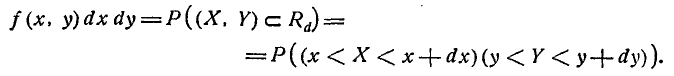
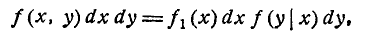
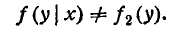
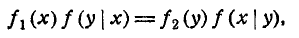
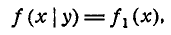
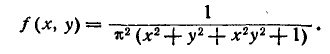
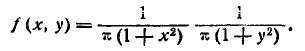
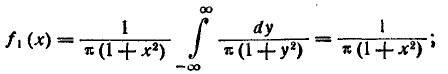
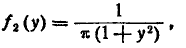
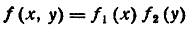
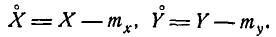
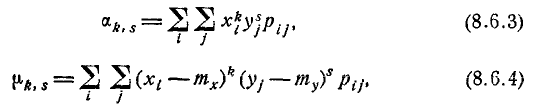
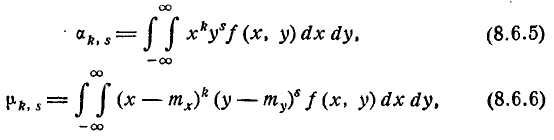
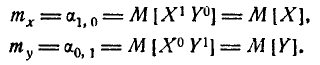
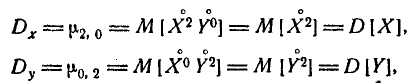
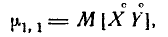
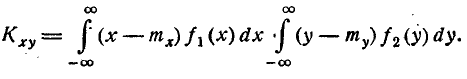
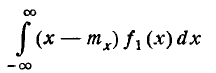
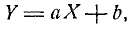
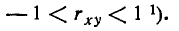
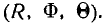
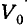 и двумя углами Ф и
и двумя углами Ф и  , определяющими направление полёта осколка в сферической системе координат.
, определяющими направление полёта осколка в сферической системе координат.