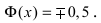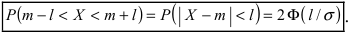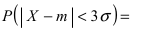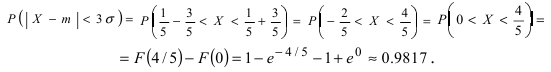| Нормальное распределение | |
|---|---|
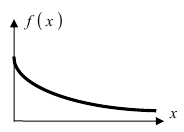
 Зеленая линия соответствует стандартному нормальному распределениюПлотность вероятности |
|
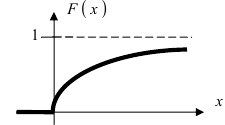
 Цвета на этом графике соответствуют графику наверхуФункция распределения |
|
| Обозначение |
 |
| Параметры |
μ — коэффициент сдвига (вещественный) σ > 0 — коэффициент масштаба (вещественный, строго положительный) |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
![{frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sqrt {2sigma ^{2}}}}right)right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/04670b14acb4ddb796469f3812ead9d9cccec275) |
| Математическое ожидание |
 |
| Медиана |
 |
| Мода |
 |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов |
 |
| Характеристическая функция |
 |
Норма́льное распределе́ние[1][2], также называемое распределением Гаусса или Гаусса — Лапласа[3], или колоколообразная кривая — непрерывное распределение вероятностей с пиком в центре и симметричными боковыми сторонами, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
,
- где параметр
— математическое ожидание (среднее значение), медиана и мода распределения, а параметр
— среднеквадратическое отклонение,
— дисперсия распределения.
Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений, которое принадлежит экспоненциальному классу распределений[4]. Многомерный случай описан в статье «Многомерное нормальное распределение».
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 

Общие сведения[править | править код]
Если величина является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то центрированное и нормированное распределение такой величины при достаточно большом числе слагаемых стремится к нормальному распределению.
Это следует из центральной предельной теоремы теории вероятностей. В окружающем нас мире часто встречаются величины, значение которых определяется совокупностью многих независимых факторов. Этот факт, а также то, что распределение считалось типичным, обычным, привели к тому, что в конце XIX века стал использоваться термин «нормальное распределение». Нормальное распределение играет заметную роль во многих областях науки, например в математической статистике и статистической физике.
Случайная величина, имеющая нормальное распределение, называется нормальной, или гауссовской, случайной величиной.
Определения[править | править код]
Стандартное нормальное распределение[править | править код]
Наиболее простой случай нормального распределения — стандартное нормальное распределение — частный случай, когда 

Множитель 






Гаусс называл стандартным нормальным распределение с 
Нормальное распределение с параметрами μ, σ[править | править код]
Каждое нормальное распределение — это вариант стандартного нормального распределения, область значений которого растягивается множителем 



Если 







Если в экспоненте плотности вероятности раскрыть скобки и учитывать, что 
Таким образом, плотность вероятности каждого нормального распределения представляет собой экспоненту квадратичной функции:
- где
Отсюда можно выразить среднее значение как 




Обозначение[править | править код]
Плотность вероятности стандартного нормального распределения (с нулевым средним и единичной дисперсией) часто обозначается греческой буквой 

Нормальное распределение часто обозначается 




Функция распределения[править | править код]
Функция распределения стандартного нормального распределения (нормальное интегральное распределение) обычно обозначается заглавной греческой буквой 
С ней связана функция ошибок (интеграл вероятности) 
![{displaystyle [-x,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e23c41ff0bd6f01a0e27054c2b85819fcd08b762)
Эти интегралы не выражаются в элементарных функциях и называются специальными функциями. Многие их численные приближения известны. См. ниже.
Функции связаны, в частности, соотношением:
.
Нормальное распределение с плотностью 


Можно использовать функцию 


.
График стандартной нормальной функции распределения 

Функция распределения стандартной нормальной случайной величины может быть разложена с помощью метода интегрирования по частям в ряд:
где знак 
Асимптотическое разложение функции распределения для больших 
Стандартное отклонение[править | править код]
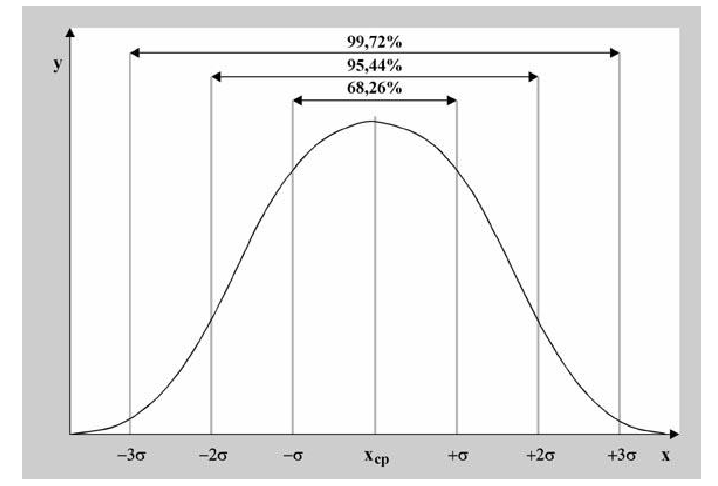
Правило 68-95-99,7.
Для нормального распределения количество значений, отличающихся от среднего на число, меньшее чем одно стандартное отклонение, составляют 68,27 % выборок. В то же время количество значений, отличающиеся от среднего на два стандартных отклонения, составляют 95,45 %, а на три стандартных отклонения — 99,73 %.
Около 68 % значений из нормального распределения находятся на расстоянии не более одного стандартного отклонения σ от среднего; около 95 % значений лежат расстоянии не более двух стандартных отклонений; и 99,7 % не более трёх. Этот факт является частным случаем правила 3 сигм для нормальной выборки.
Более точно, вероятность получить нормальное число в интервале между 

С точностью до 12 значащих цифр значения для 
 |
 |
 |
 |
OEIS |
|---|---|---|---|---|
| 1 | 0,682689492137 | 0,317310507863 |
3,15148718753 |
A178647 |
| 2 | 0,954499736104 | 0,045500263896 |
21,9778945080 |
A110894 |
| 3 | 0,997300203937 | 0,002699796063 |
370,398347345 |
A270712 |
| 4 | 0,999936657516 | 0,000063342484 |
15787.1927673 |
|
| 5 | 0,999999426697 | 0,000000573303 |
1744277,89362 |
|
| 6 | 0,999999998027 | 0,000000001973 |
506797345,897 |
Свойства[править | править код]
Моменты[править | править код]
Моментами и абсолютными моментами случайной величины 




Если 


Здесь 




Центральные абсолютные моменты для неотрицательных целых 
Последняя формула справедлива также для произвольных 
Преобразование Фурье и характеристическая функция[править | править код]
Преобразование Фурье нормальной плотности вероятности 


- где
есть мнимая единица.
Если математическое ожидание 


В теории вероятности, преобразование Фурье плотности распределения действительной случайной величины 




Бесконечная делимость[править | править код]
Нормальное распределение является бесконечно делимым.
Если случайные величины 








Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.
Максимальная энтропия[править | править код]
Нормальное распределение имеет максимальную дифференциальную энтропию среди всех непрерывных распределений, дисперсия которых не превышает заданную величину[11][12].
Правило трёх сигм для гауссовской случайной величины[править | править код]
График плотности вероятности нормального распределения и процент попадания случайной величины на отрезки, равные среднеквадратическому отклонению.
Правило трёх сигм (
- где
— математическое ожидание и параметр нормальной случайной величины.
Более точно — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.
Моделирование нормальных псевдослучайных величин[править | править код]
При компьютерном моделировании, особенно при применении метода Монте-Карло, желательно использовать величины, распределенные по нормальному закону. Многие алгоритмы дают стандартные нормальные величины, так как нормальную величину 
- где Z — стандартная нормальная величина.
Алгоритмы также используют различные преобразования равномерных величин.
Простейшие приближённые методы моделирования основываются на центральной предельной теореме. Если сложить достаточно большое количество независимых одинаково распределённых величин с конечной дисперсией, то сумма будет иметь распределение, близкое к нормальному. Например, если сложить 100 независимых стандартно равномерно распределённых случайных величин, то распределение суммы будет приближённо нормальным.
Для программного генерирования нормально распределённых псевдослучайных величин предпочтительнее использовать преобразование Бокса — Мюллера. Оно позволяет генерировать одну нормально распределённую величину на базе одной равномерно распределённой.
Также существует алгоритм Зиккурат, который работает даже быстрее преобразования Бокса — Мюллера. Тем не менее, сложнее в реализации, но его применение оправдано в случаях, когда требуется генерирование очень большого числа неравномерно распределённых случайных чисел.
Нормальное распределение в природе и приложениях[править | править код]
Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:
- отклонение при стрельбе;
- погрешности измерений (однако погрешности некоторых измерительных приборов имеют иное распределение);
- некоторые характеристики живых организмов в популяции.
Такое широкое распространение этого распределения связано с тем, что оно является бесконечно делимым непрерывным распределением с конечной дисперсией. Поэтому к нему в пределе приближаются некоторые другие, например биномиальное и пуассоновское. Этим распределением моделируются многие недетерминированные физические процессы[13].
Многомерное нормальное распределение используется при исследовании многомерных случайных величин (случайных векторов). Одним из многочисленных примеров таких приложений является исследование параметров личности человека в психологии и психиатрии.
Связь с другими распределениями[править | править код]
- Отношение квадратов двух стандартных нормальных случайных величин имеет распределение Фишера со степенями свободы
История[править | править код]
Впервые нормальное распределение как предел биномиального распределения при 
См. также[править | править код]
- Аддитивный белый гауссовский шум
- Логнормальное распределение
- Равномерное распределение
- Центральная предельная теорема
- Двумерное нормальное распределение
- Многомерное нормальное распределение
- Распределение хи-квадрат
- Статистический критерий
- Частотное распределение
Примечания[править | править код]
- ↑ Вентцель Е. С. Теория вероятностей. — 10-е изд., стереотипное.. — М.: Academia, 2005. — 576 с. — ISBN 5-7695-2311-5.
- ↑ Ширяев А. Н. Вероятность. — М.: Наука, 1980.
- ↑ 1 2 Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 139—140.
- ↑ Wasserman L. All of Statistics. — New York, NY: Springer, 2004. — С. 142. — 433 с. — ISBN 978-1-4419-2322-6.
- ↑ Доказательство см. Гауссов интеграл
- ↑ Halperin, Hartley & Hoel, 1965, item 7.
- ↑ McPherson (1990)
- ↑ Wolfram|Alpha: Computational Knowledge Engine. Wolframalpha.com. Дата обращения: 3 марта 2017.
- ↑ Bryc (1995, p. 23)
- ↑ Bryc (1995, p. 24)
- ↑ Cover, Thomas M.; Thomas, Joy A. Elements of Information Theory. — John Wiley and Sons, 2006. — С. 254.
- ↑ Park, Sung Y.; Bera, Anil K. Maximum Entropy Autoregressive Conditional Heteroskedasticity Model (англ.) // Journal of Econometrics (англ.) (рус. : journal. — Elsevier, 2009. — P. 219—230. Архивировано 7 марта 2016 года.
- ↑ Талеб Н. Н. Чёрный лебедь. Под знаком непредсказуемости = The Black Swan: The Impact of the Highly Improbable. — КоЛибри, 2012. — 525 с. — ISBN 978-5-389-00573-0.
- ↑ Королюк, 1985, с. 135.
- ↑ Галкин В. М., Ерофеева Л. Н., Лещева С. В. Оценки параметра распределения Коши // Труды Нижегородского государственного технического университета им. Р. Е. Алексеева. — 2014. — № 2(104). — С. 314—319. — УДК 513.015.2(G).
- ↑ Lukacs, Eugene. A Characterization of the Normal Distribution (англ.) // The Annals of Mathematical Statistics (англ.) (рус. : journal. — 1942. — Vol. 13, no. 1. — P. 91—3. — ISSN 0003-4851. — doi:10.1214/aoms/1177731647. — JSTOR 2236166.
- ↑ Lehmann, E. L.ruen. Testing Statistical Hypotheses. — 2nd. — Springer (англ.) (рус., 1997. — С. 199. — ISBN 978-0-387-94919-2.
- ↑ The doctrine of chances; or, a method of calculating the probability of events in play, L., 1718, 1738, 1756; L., 1967 (репродуцир. изд.); Miscellanea analytica de scriebus et quadraturis, L., 1730.
Литература[править | править код]
- Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
- Halperin, Max; Hartley, Herman O.; Hoel, Paul G. Recommended Standards for Statistical Symbols and Notation. COPSS Committee on Symbols and Notation (англ.) // The American Statistician (англ.) (рус. : journal. — 1965. — Vol. 19, no. 3. — P. 12—14. — doi:10.2307/2681417. — JSTOR 2681417.
- McPherson, Glen. Statistics in Scientific Investigation: Its Basis, Application and Interpretation (англ.). — Springer-Verlag, 1990. — ISBN 978-0-387-97137-7.
- Bryc, Wlodzimierz. The Normal Distribution: Characterizations with Applications (англ.). — Springer-Verlag, 1995. — ISBN 978-0-387-97990-8.
Ссылки[править | править код]
- Таблица значений функции стандартного нормального распределения
- Онлайн расчёт вероятности нормального распределения
Плотность распределения вероятностей непрерывной случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).
Плотностью распределения вероятностей непрерывной случайной величины
называют функцию
– первую производную от функции распределения
:
Из этого определения следует, что
функция распределения является первообразной для плотности распределения.
Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.
Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина
примет
значение, принадлежащее интервалу
равна
определенному интегралу от плотности распределения, взятому в пределах от
до
:
Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу
, равна площади криволинейной трапеции, ограниченной
осью
, кривой распределения
и прямыми
и
.
В частности, если
– четная
функция и концы интервала симметричны относительно начала координат, то:
Зная плотность распределения
можно найти
функцию распределения
по формуле:
Свойства плотности распределения
Свойство 1.
Плотность
распределения – неотрицательная функция:
Свойство 2.
Несобственный
интеграл от плотности распределения в пределах от
до
равен единице:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Интегральная функция распределения вероятностей
Примеры решения задач
Пример 1
Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики F(x) и f(x);
4) найти
математическое ожидание и дисперсию X;
5) найти
вероятность того, что X примет значение из
интервала (α,β):
α=1; β=1.7
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем
отметить, что:
Остается
найти выражение для
, когда
принадлежит
интервалу
.
Получаем:
3) Построим графики
и
:
График плотности распределения
График функции распределения
4)
Математическое ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
5)
Вероятность того, что случайная величина примет значение из интервала
:
Пример 2
Плотность
распределения вероятности непрерывной случайной величины равна
, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).
Решение
Нормировочный множитель
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Плотность
вероятности:
Математическое
ожидание находим по формуле:
Для
нашего примера:
Дисперсию
можно найти по формуле:
Пример 3
Непрерывная
случайная величина
имеет плотность распределения:
Найти
величину a, вероятность P(X<0) и математическое
ожидание X.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Постоянный
параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Плотность
вероятности имеет вид:
Вероятность:
Математическое
ожидание находим по формуле:
Для
нашего примера:
Задачи контрольных и самостоятельных работ
Задача 1
Плотность
распределения непрерывной случайной величины X имеет вид:
Найти:
а)
параметр a;
б)
функцию распределения F(x);
в)
вероятность попадания случайной величины X в интервал (6.5; 11);
г)
математическое ожидание M(X) и дисперсию D(X);
Построить
график функций f(x) и F(x).
Задача 2
Задана
функция распределения непрерывной случайной величины:
Найти и
построить график функции плотности распределения вероятностей.
Задача 3
Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).
Задача 4
Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).
α=1,β=2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 5
Непрерывная
случайная величина
задана плотностью распределения вероятностей.
Требуется
найти:
– функцию
распределения вероятностей;
–
математическое ожидание;
–
дисперсию;
– среднее
квадратическое отклонение;
– вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;
–
построить графики функции распределения и плотности распределения вероятностей.
Задача 6
Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).
Задача 7
Случайная
величина X~N(a,σ)
a=25;
σ=4; α=13; β=30; δ=0.1.
Требуется:
–
составить функцию плотности распределения и построить ее график;
– найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);
– найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.
Задача 8
Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:
Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Случайная
величина X задана функцией распределения вероятностей F(x).
Требуется:
1. Найти
функцию плотности распределения f(x).
2. Найти M(X).
3. Найти
вероятность P(α<X<β)
4.
Построить графики f(x) и F(x).
α=2, β=4.5
Задача 10
Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).
M(X)=-1; D(X)=8
Задача 11
Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:
а) найти
параметр C;
б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);
в)
построить графики функций F(x) и f(x);
г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);
д)
вычислить вероятность попадания в интервал P(a≤x≤b)
е)
определить, квантилем какого порядка является точка xp;
ж)
вычислить квантиль порядка p
a=π/4; b=π/3; xp=π/2; p=0.75
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
104
ЛЕКЦИЯ
10
Нормальное
распределение. Функция
нормального распределения. Функция
Лапласа. Числовые характеристики
нормального распределения. Вероятность
попадания нормально распределенной
случайной величины в заданный интервал.
Правило трех сигм. Распределения,
связанные с нормальным: распределения
Стьюдента, Пирса и Фишера. Характеристическая
функция нормального распределения.
8.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
8.1.
Функция нормального распределения
Одним
из наиболее часто встречающихся
распределений является нормальное
распределение. Оно играет большую роль
в теории вероятностей и ее приложениях.
Фундаментальная роль, которую играет
нормальное распределение, объясняется
тем, что суммы случайных величин с ростом
числа слагаемых при довольно широких
предположениях ведут себя асимптотически
нормально (см. тему “Центральная
предельная теорема”).
Плотность
функции нормального распределения
имеет вид
.
(8.1)
Функция нормального распределения
имеет вид
.
(8.2)
Однако часто вместо
функции нормального распределения
используется функция Лапласа.
Пусть
a=0,
=1,
то получим
.
(8.3)
Такая
функция называется стандартным
нормальным распределением.
Запишем данную функцию в следующем виде
.
Поскольку
F0(+)=1,
то в силу
симметрии первое слагаемое равно 0,5, а
второе слагаемое есть функция Лапласа
.
(8.4)
Таким
образом,
.
Отсюда
получаем равенство
,
(8.5)
связывающее функцию
нормального распределения и функцию
Лапласа.
Для
стандартного нормального распределения
и функции Лапласа существуют обширные
таблицы. Однако здесь нужно иметь в
виду, что иногда вместо рассмотренных
функций используют функции
.
(8.6)
или
интеграл ошибок
.
(8.7)
Замечание.
Открытие нормального распределения
связано с именами
К.
Гаусса
и П.
Лапласа,
у которых оно впервые появилось связи
с исследованием по теории ошибок и
методу наименьших квадратов. Поэтому
нормальное распределение называют еще
распределением
Лапласа-Гаусса,
или просто распределением
Гаусса
или Лапласа.
Найдем
математическое
ожидание
нормального распределения:

Вычислим
дисперсию:

Таким
образом,
M[X]
= a,
D[X]
= 2,
т.е.
нормальное распределение характеризуется
двумя параметрами: a,
имеющему
смысл математического ожидания, и ,
имеющему
смысл среднего квадратичного отклонения.
Рис.
8.1
График плотности функции нормального
распределения имеет следующий вид
(кривая Гаусса).
Максимум будет при x=a,
точки перегиба в точках
a–
и a+.
Кривая симметрична
относительно прямой x=a.
С уменьшением
кривая становится все
более островершинной.
8.2.
Вероятность попадания нормально
распределенной случайной величины
в заданный интервал
Известно,
что если случайная величина X
задана
плотностью распределения f(x),
то вероятность
того, что X
примет
значение, принадлежащее интервалу
(,),
имеет вид
.
В
случае нормального распределения эта
формула примет следующий вид
.
(8.8)
Часто
требуется вычислить вероятность того,
что отклонение случайной величины X
по абсолютной
величине меньше заданного положительного
числа
,
т.е. требуется
найти вероятность осуществления
неравенства |X–a|<.
Заметим,
что неравенство равносильным ему двойным
неравенством a–<X<a+.
Тогда
.
Таким
образом,
.
(8.9)
В частности, если ,
то
P(|X–a|<)
= 2(1)
= 0,6827;
если
2,
то
P(|X–a|<2)
= 2(2)
= 0,9545;
если
,
то
P(|X–a|<3)
= 2(3)
= 0,9973.
Последнее
равенство показывает, что во многих
практических вопросах при рассмотрении
нормального распределения можно
пренебречь возможностью отклонения
случайной величины от a
больше,
чем 3
Это есть
т.н. правило “трех
сигм”.
Например,
каждому кто занимался измерениями,
встречался с ситуацией, когда появляется
“дикое
значение”.
В связи с этим возникает проблема:
исключать это значение или его следует
оставить. Так, при разработке норматива
времени для изготовления одной детали
проделали следующие измерения: 5,0;
4,8; 5,2; 5,3; 5,0; 6,1. Последнее
число сильно отличается от других. В
связи с этим возникает вопрос, не скрыта
ли здесь ошибка в измерениях. Вычислим
среднее значение
и среднее квадратичное отклонение
=0,46.
После этого
построим “трехсигмовый” интервал:
(4,84; 6,61). Поскольку значение x=6,1
не выходит
за пределы трехсигмовой зоны, то его
нельзя считать “диким”.
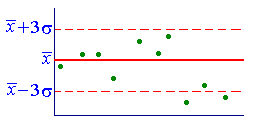
пример. На конвейере изготовляются
детали. На основании статистических
данных контроля деталей вычисляют
среднее квадратичное отклонение .
Затем
строят прямую средней линии, окаймленную
трехсигмовой полосой. Если точки
контрольных измерений находятся внутри
трехсигмовой полосы, то технологический
процесс следует считать стабильным и
качество продукции высоким. Если точки
близки к контрольным линиям, но не
выходят за пределы трехсигмовой зоны,
то это указывает на разладку технологического
процесса. Если же точки выходят за
пределы трехсигмовой зоны, то это
означает, что идет брак.
Пример
8.1. Автомат
изготовляет шарики. Шарик считается
годным, если отклонение диаметра шарика
X от
проектного по абсолютной величине не
превышает 0,7 мм.
Считая, что случайная величина X
распределена
нормально со средним квадратичным
отклонением 0,4 мм,
определить, сколько процентов годных
шариков изготовляет автомат.
Решение.
Поскольку =0,4
мм
и =0,7
мм,
то
Следовательно,
автомат изготовляет 92% годных деталей.
8.3.
Распределения, связанные с нормальным
8.3.1.
Распределение Пирсона (2-распределение)
Пусть
независимые случайные величины U1,
U2,
…, Uk
описываются
стандартным нормальным распределением:
Ui=N(0,1).
Тогда
распределение суммы квадратов этих
величин
(8.10)
называется
распределением
2
(“хи-квадрат”)
с k
степенями
свободы.
В явном виде плотность функции этого
распределения имеет вид
(8.11)
где
– гамма-функция;
в частности, (n+1)=n!.
Рис.
8.2
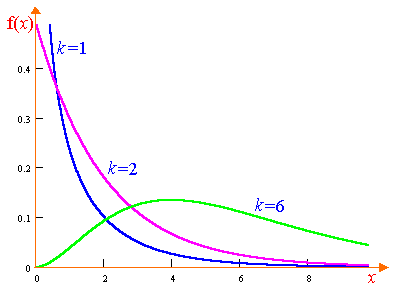
Распределение Пирсона
определяется одним параметром – числом
степеней свободы k.
Графики этой функции
изображены на рис. 8.2. Числовые
характеристики распределения Пирсона:
Если
случайные величины 2(k1)
и 2(k2)
независимы, то
.
Отметим,
что с увеличением числа степеней свободы
распределение Пирсона постепенно
приближается к нормальному.
8.3.2.
Распределение Стьюдента (t-распределение)
Пусть
U
–стандартная
нормально распределенная случайная
величины, U=N(0,1),
а 2
– случайная
величина, имеющая 2-распределение
с k
степенями
свободы, причем U
и 2
независимые
величины. Тогда распределение величины
(8.12)
называется
распределением
Стьюдента
(t-распределением)
с k
степенями
свободы.
В явном виде плотность функции
распределения Стьюдента имеет вид
Рис.
8.3
(8.13)
График
этой функции изображен на рис. 8.3.
Числовые
характеристики распределения Стьюдента:
Отметим,
что с возрастанием числа степеней
свободы распределение Стьюдента быстро
приближается к нормальному.
8.3.3.
Распределение Фишера (F-распределение)
Пусть
2(k1)
и 2(k2)
– независимые
случайные величины, имеющие 2-распределение
соответственно с k1
и k2
степенями
свободы. Распределение величины
(8.14)
называется
распределением
Фишера
(F-распределением)
со
степенями
свободы k1
и
k2.
В явном виде плотность распределения
Фишера имеет вид
(8.15)
График
этой функции изображен на рис. 8.4.
Числовые
характеристики распределения Фишера:
О
Рис.
8.4
тметим, что между случайными
величинами, имеющими нормальное
распределение, распределение Пирсона,
Стьюдента и Фишера, имеют место
соотношения:
8.4*.
Характеристическая функция
нормального
распределения
Пусть
случайная величина
распределена
по стандартному нормальному распределению.
Тогда для характеристической функции
получим
.
Делая
замену y=x–it,
получим
.
Из
теории функций комплексной переменной
известно, что
.
Поэтому
окончательно получаем
.
Как
мы видели, если случайная величина
распределена
по стандартному нормальному закону, то
случайная величина =t+m
распределена
но нормальному закону с параметрами m
и .
Тогда
характеристические функции f(t)
и f(t)
связаны
по свойству 2 соотношением
,
или,
окончательно получаем, что характеристическая
функция для нормального распределения
имеет вид
.
(8.16)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Нормальный закон распределения:
Нормальный закон распределения имеет плотность вероятности
где
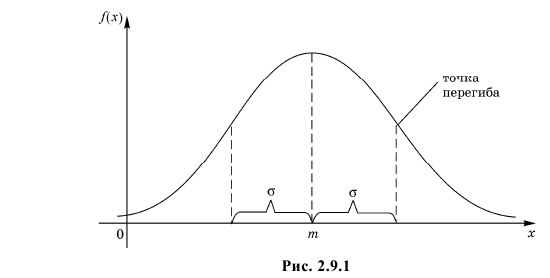
График функции плотности вероятности (2.9.1) имеет максимум в точке 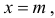

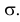
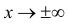
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр 
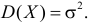
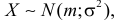

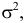
где 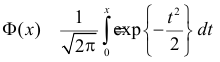
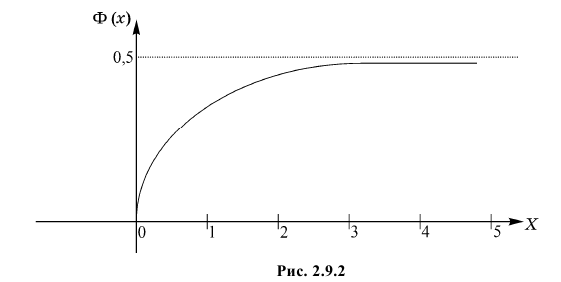
Значения функции 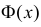
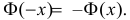
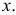
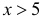
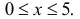
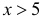
Если 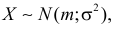
Пример:
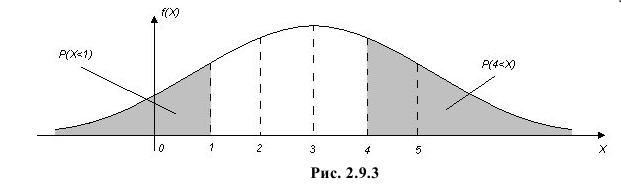
Случайная величина X имеет нормальный закон распределения 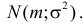
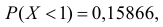
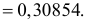
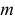
Решение. Воспользуемся формулой (2.9.2):
Так как 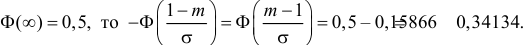
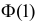
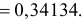
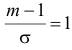
Аналогично 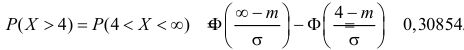
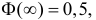
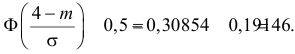
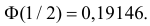
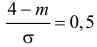
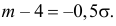
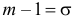
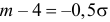
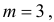
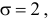
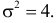
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
Ответ.
Пример:
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 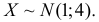
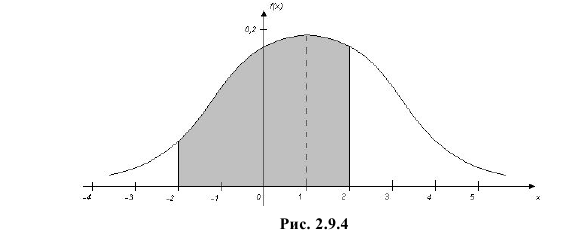
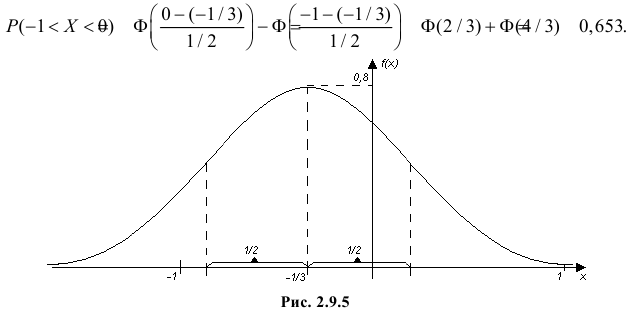
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна
Ответ.
Пример:
Функция плотности вероятности случайной величины X имеет вид
Требуется определить коэффициент 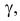
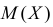
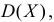
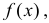
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 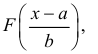
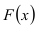
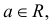
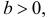
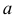
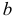
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице:
Преобразуем выражение в показателе степени, выделяя полный квадрат:
Тогда (2.9.5) можно записать в виде
Сделаем замену переменных так, чтобы 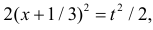
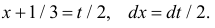
Умножим и разделим левую часть равенства на 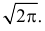
Так как 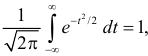
Поэтому
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 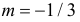
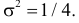
Ответ.
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 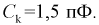
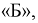
Решение.
Статистическими исследованиями в цеху установлено, что 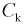
Чтобы вычислить количество транзисторов, попадающих в группу 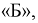
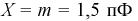
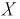
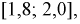
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения
дает 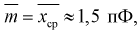
Обозначая 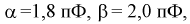
Тогда количество транзисторов 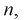
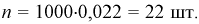
Нормальное распределение и его свойства
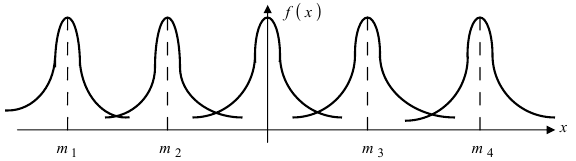
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, “от 180 до 181 включительно”.
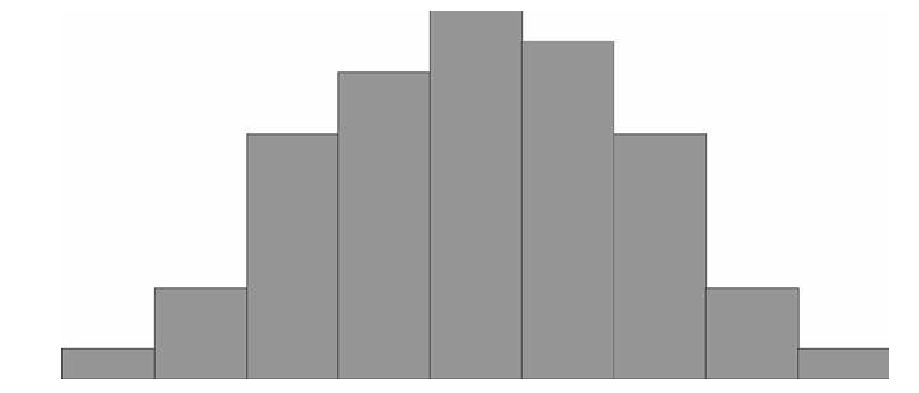
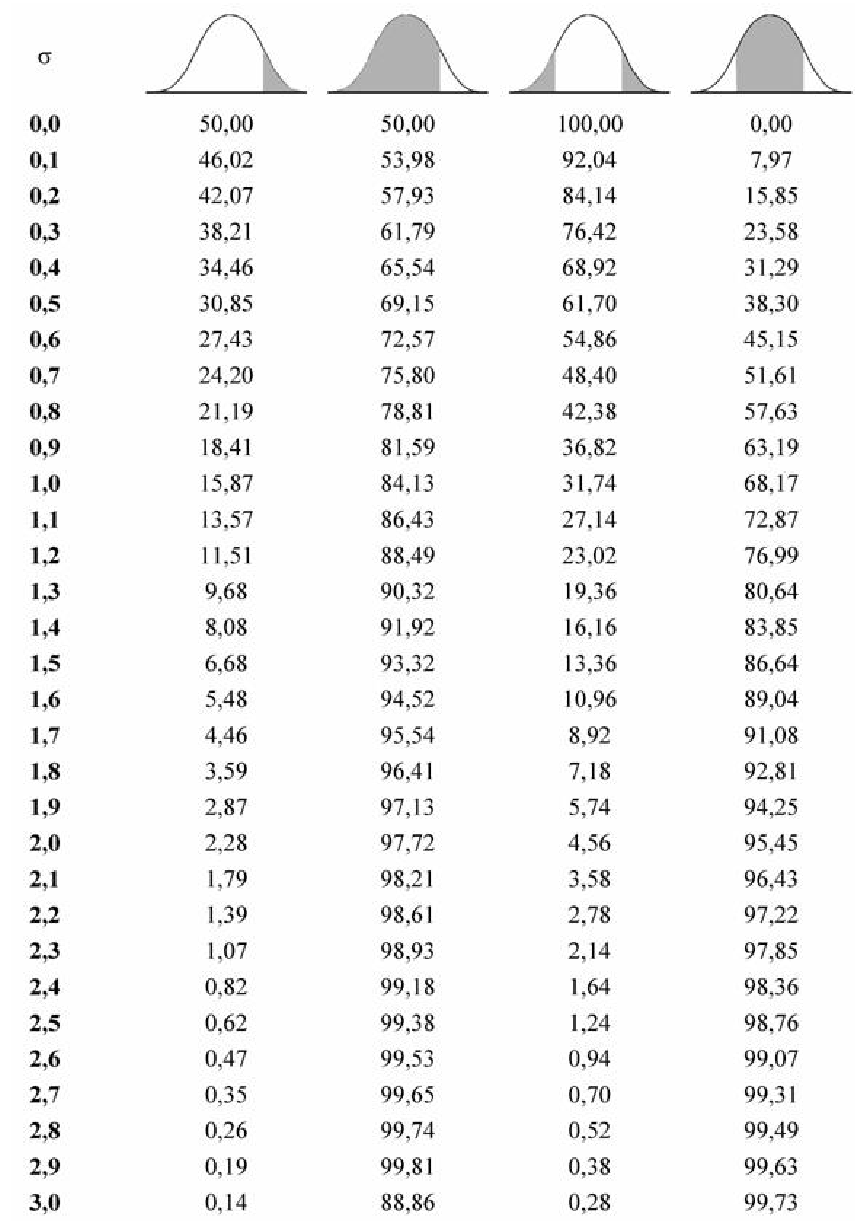
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, “оплывет” вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади “ломтика” кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста – достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона – чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько “популярен” выбранный нами рост. Напомним, что мода – самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
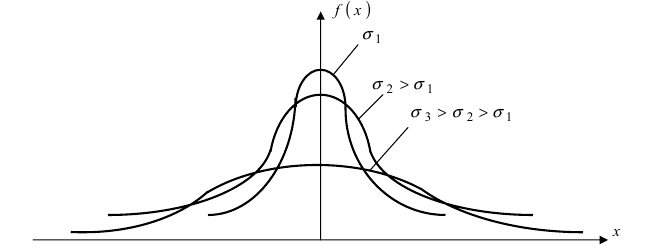
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 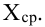
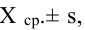
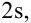
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой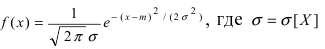
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
Выясним геометрический смысл параметров 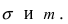
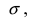
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 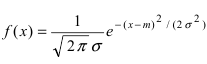
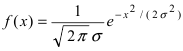
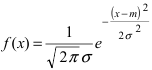
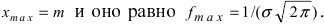
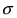
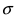
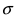
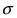
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
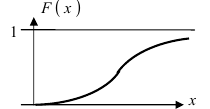
Интегральная функция нормального распределения имеет вид:
График функции распределения имеет вид (Рис. 10):
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 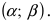
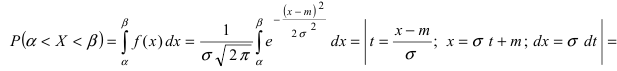
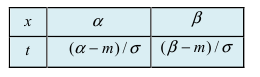
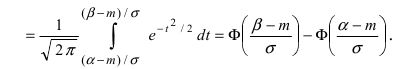
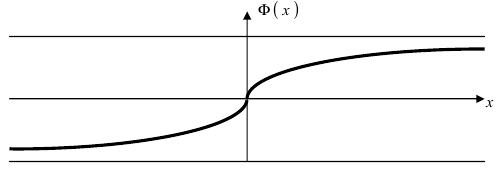
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 – график функции Лапласа проходит через начало координат.
- Ф (-х) = – Ф(х) – функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
– график функции Лапласа имеет горизонтальные асимптоты
Следовательно, график функции Лапласа имеет вид (Рис. 11):
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 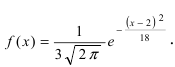
Решение:
Согласно условиям задачи 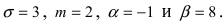
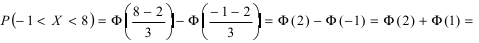
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 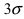
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 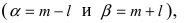
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 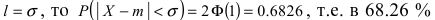
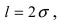
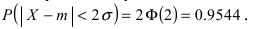
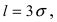
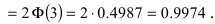
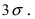
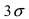
Показательный закон распределения
Определение: Закон распределения, определяемый фу нкцией распределения:
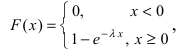
График экспоненциального закона распределения имеет вид (Рис. 12):
Рис. 12. График функции распределения для случая экспоненциального закона.
Дифференциальная функция распределения (плотность вероятности) имеет вид: 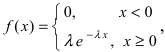
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 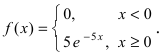
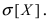
Решение:
Интегральная функция распределения 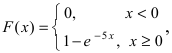
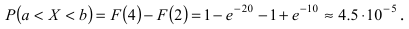
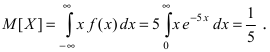
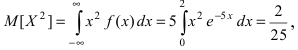
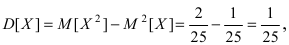
отклонение 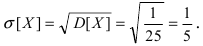
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Пусть $X$ — непрерывная случайная величина.
Определение 1
Случайная величина $X$ имеет нормальное распределение (распределение Гаусса), если плотность её распределения определяется формулой:
[varphi left(xright)=frac{1}{sqrt{2pi }sigma }e^{frac{-{(x-a)}^2}{2{sigma }^2}}]
Здесь $aϵR$ — математическое ожидание, а $sigma >0$ — среднее квадратическое отклонение.
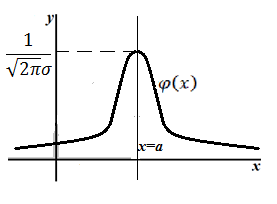
Плотность нормального распределения.
Покажем, что эта функция действительно является плотностью распределения. Для этого проверим следующее условие:
Рассмотрим несобственный интеграл $intlimits^{+infty }_{-infty }{frac{1}{sqrt{2pi }sigma }e^{frac{-{(x-a)}^2}{2{sigma }^2}}dx}$.
Сделаем замену: $frac{x-a}{sigma }=t, x=sigma t+a, dx=sigma dt$.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Так как $fleft(tright)=e^{frac{-t^2}{2}}$ четная функция, то
Равенство выполняется, значит, функция $varphi left(xright)=frac{1}{sqrt{2pi }sigma }e^{frac{-{(x-a)}^2}{2{sigma }^2}}$ действительно является плотностью распределения некоторой случайной величины.
Рассмотрим некоторые простейшие свойства функции плотности вероятности нормального распределения $varphi left(xright)$:
- График функции плотности вероятности нормального распределения симметричен относительно прямой $x=a$.
- Функция $varphi left(xright)$ достигает максимума при $x=a$, при этом $varphi left(aright)=frac{1}{sqrt{2pi }sigma }e^{frac{-{(a-a)}^2}{2{sigma }^2}}=frac{1}{sqrt{2pi }sigma }$
- Функция $varphi left(xright)$ убывает, при $x>a$, и возрастает, при $x
- Функция $varphi left(xright)$ имеет точки перегиба при $x=a+sigma $ и $x=a-sigma $.
- Функция $varphi left(xright)$ асимптотически приближается к оси $Ox$ при $xto pm infty $.
- Схематический график выглядит следующим образом (рис. 1).
«Нормальное распределение» 👇
Рисунок 1. Рис. 1. График плотности нормального распределения
!!! Заметим, что, если $a=0$, то график функции симметричен относительно оси $Oy$. Следовательно, функция $varphi left(xright)$ четна.
Функция нормального распределения вероятности.
Для нахождения функции распределения вероятности при нормальном распределении воспользуемся следующей формулой:
Следовательно,
Определение 2
Функция $F(x)$ называется стандартным нормальным распределением, если $a=0, sigma =1$, то есть:
[Fleft(xright)=frac{1}{sqrt{2pi }}intlimits^x_{-infty }{e^{frac{-t^2}{2}}dt}=frac{1}{sqrt{2pi }}left(intlimits^0_{-infty }{e^{frac{-t^2}{2}}dt}+intlimits^x_0{e^{frac{-t^2}{2}}dt}right)=0,5+Ф(x)]
Здесь $Фleft(xright)=frac{1}{sqrt{2pi }}intlimits^x_0{e^{frac{-t^2}{2}}dt}$ – функция Лапласса.
Определение 3
Функция $Фleft(xright)=frac{1}{sqrt{2pi }}intlimits^x_0{e^{frac{-t^2}{2}}dt}$ называется интегралом вероятности.
Числовые характеристики нормального распределения.
Математическое ожидание: $Mleft(Xright)=a$.
Дисперсия: $Dleft(Xright)={sigma }^2$.
Среднее квадратическое распределение: $sigma left(Xright)=sigma $.
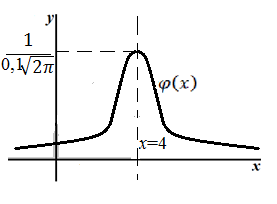
Пример 1
Пример решения задачи на понятие нормального распределения.
Задача 1: Длина пути $X$ представляет собой случайную непрерывную величину. $X$ распределена по нормальному закону распределения среднее значение которого равно $4$ километра, а среднее квадратическое отклонение равно $100$ метров.
- Найти функцию плотности распределения $X$.
- Построить схематически график плотности распределения.
- Найти функцию распределения случайной величины $X$.
- Найти дисперсию.
Решение:
- Для начала представим все величины в одном измерении: 100м=0,1км
Из определения 1, получим:
[varphi left(xright)=frac{1}{0,1sqrt{2pi }}e^{frac{-{(x-4)}^2}{0,02}}]
(так как $a=4 км, sigma =0,1 км)$
- Используя свойства функции плотности распределения, имеем, что график функции $varphi left(xright)$ симметричен относительно прямой $x=4$.
Максимум функция достигает в точке $left(a,frac{1}{sqrt{2pi }sigma }right)=(4, frac{1}{0,1sqrt{2pi }})$
Схематический график имеет вид:
Рисунок 2.
- По определению функции распределения $Fleft(xright)=frac{1}{sqrt{2pi }sigma }intlimits^x_{-infty }{e^{frac{-{(t-a)}^2}{2{sigma }^2}}dt}$, имеем:
[Fleft(xright)=frac{1}{0,1sqrt{2pi }}intlimits^x_{-infty }{e^{frac{-{(t-4)}^2}{0,02}}dt}]
- $Dleft(Xright)={sigma }^2=0,01$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме










![{displaystyle Phi (x)={frac {1}{2}}left[1+operatorname {erf} left({frac {x}{sqrt {2}}}right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7831a9a5f630df7170fa805c186f4c53219ca36)
![{displaystyle F(x)=Phi left({frac {x-mu }{sigma }}right)={frac {1}{2}}left[1+operatorname {erf} left({frac {x-mu }{sigma {sqrt {2}}}}right)right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a75caa2df3861960f6c6a5ac91f0b0fa6d79504)


![{displaystyle Phi (x)={frac {1}{2}}+{frac {1}{sqrt {2pi }}}cdot e^{-x^{2}/2}left[x+{frac {x^{3}}{3}}+{frac {x^{5}}{3cdot 5}}+cdots +{frac {x^{2n+1}}{(2n+1)!!}}+cdots right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b755fcac449fe404b290943b01b01eab9c50440a)



![{displaystyle mathbb {E} left[X^{p}right]={begin{cases}0&p=2n+1,\sigma ^{p},left(p-1right)!!&p=2n.end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39f9a1d5eadfbc872b3cd41f8135576e3123bc4)
![{displaystyle mathbb {E} left[left|Xright|^{p}right]=sigma ^{p},left(p-1right)!!cdot left.{begin{cases}{sqrt {frac {2}{pi }}}&p=2n+1,\1&p=2n.end{cases}}right}=sigma ^{p}cdot {frac {2^{frac {p}{2}}Gamma left({frac {p+1}{2}}right)}{sqrt {pi }}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45215d47f1e0fc958abfae9a8d7137995cf90a8)







![{displaystyle t={frac {{overline {X}}-mu }{S/{sqrt {n}}}}={frac {{frac {1}{n}}(X_{1}+cdots +X_{n})-mu }{sqrt {{frac {1}{n(n-1)}}left[(X_{1}-{overline {X}})^{2}+cdots +(X_{n}-{overline {X}})^{2}right]}}}sim t_{n-1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36ff0d3c79a0504e8f259ef99192b825357914d7)




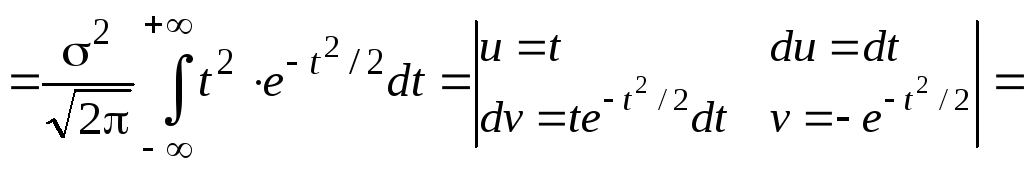


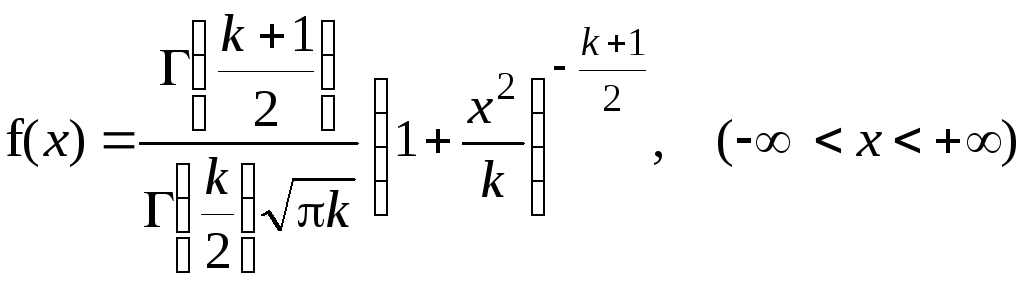






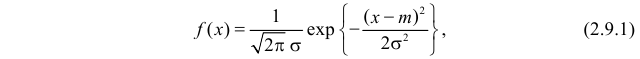
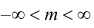
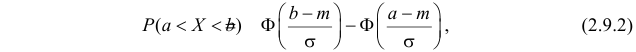
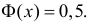
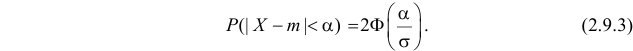
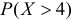
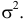
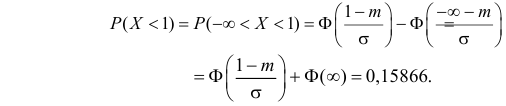
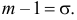
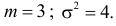
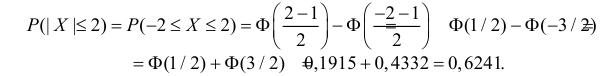
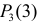
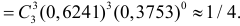
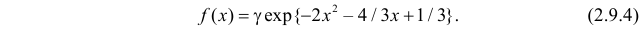
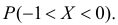
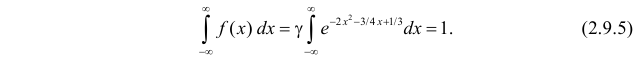
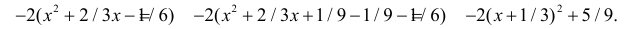
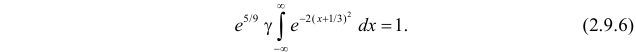

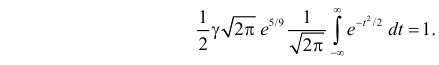

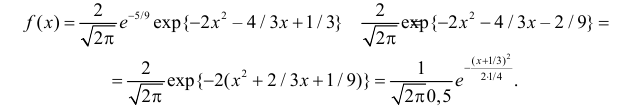
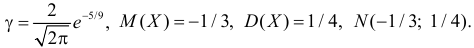
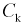
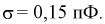
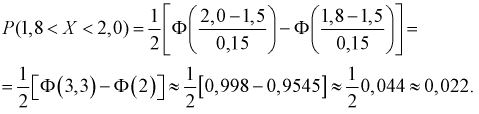
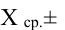
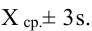
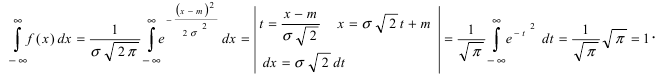
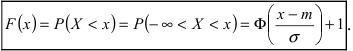
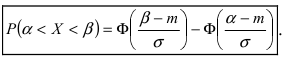
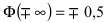 – график функции Лапласа имеет горизонтальные асимптоты
– график функции Лапласа имеет горизонтальные асимптоты